9.3: Теорема Гаусса

Цілі навчання

• Поясніть просту і загальну форму теореми Гаусса

Інтегральні закони збереження

Ми висловили збереження заряду та енергії-імпульсу в умовах нульових розбіжностей,

$$\frac{\partial J^a}{\partial x^a} = 0$$

$$\frac{\partial T^{ab}}{\partial x^a} = 0$$

Вони виражаються в терміні похідних. Похідна функції в певний момент залежить лише від поведінки функції поблизу цієї точки, тому це локальні твердження збереження. Закони збереження також можуть бути викладені глобально: загальна кількість чогось залишається постійною. Беручи заряд як приклад, спостерігач$o$ визначає координати Мінковського$(t, x, y, z)$, а в той час t1 говорить, що загальна сума заряду в якомусь регіоні становить

$$q(t_1) = \int_{t_1}J^a dS_a$$

де індекс$t_1$ означає, що інтеграл повинен бути оцінений по поверхні одночасності$t = t_1$, і$dS_a = (dx dy dz, 0, 0, 0)$ є елементом$3$ -обсягу, вираженим у вигляді ковектора. Заряд в якийсь більш пізній час$t_2$ буде дано аналогічним інтегралом. Якщо заряд зберігається, і якщо наш регіон оточений порожнім регіоном, через який не надходить або виходити плата, то ми повинні мати$q(t_2) = q(t_1)$.

Проста форма теореми Гаусса

Зв'язок між локальними і глобальними законами збереження забезпечується теоремою під назвою теорема Гаусса. У своєму курсі з електромагнетизму ви вивчили закон Гаусса, який пов'язує електричний потік через замкнуту поверхню з зарядом, що міститься всередині поверхні. У разі, коли ніяких зарядів немає, це говорить про те, що флюс через таку поверхню скасовується назовні.

Малюнок$\PageIndex{1}$: Три рядки заходять, а три виходять. Це можуть бути лінії полів або лінії світу.

Інтерпретація полягає в тому, що оскільки лінії полів починаються або закінчуються лише на зарядах, відсутність будь-яких зарядів означає, що лінії не можуть починатися або закінчуватися, і тому, як на малюнку$\PageIndex{1}$, будь-яка лінія поля, яка входить на поверхню (сприяючи деякому негативному потоку), повинна врешті-решт повернутися (створюючи деяку позитивну флюс, який скасовує негатив). Але немає нічого про фігуру$\PageIndex{1}$, яка вимагає її інтерпретації як креслення ліній електричного поля. Це може бути так само легко малюнок світовихліній деяких заряджених частинок в$1 + 1$ розмірах. Нижня частина прямокутника буде поверхнею$t_1$ вгорі$t_2$. У нас є$q(t_1) = 3$ і$q(t_2) = 3$ так само.

Для простоти почнемо з дуже обмеженої версії теореми Гаусса. Нехай векторне поле$J^a$ буде визначено у двох вимірах. (Нам байдуже, чи два виміри є як просторовими, так і одним просторовим і одноразовим; тобто теорема Гаусса не залежить від підпису метрики.) $R$Дозволяти прямокутної області, і нехай$S$ буде її межа. Визначте потік поля через$S$ як

$$\Phi = \int_{S}J^a dS_a$$

де інтеграл повинен бути прийнятий на всі чотири сторони, а ковектор$dS_a$ вказує назовні. Якщо поле має нульову розбіжність$\frac{\partial J^a}{\partial x^a} = 0$, то потік дорівнює нулю.

Доказ: Визначте координати$x$ та$y$ вирівняйте його за допомогою прямокутника. Уздовж верхньої частини прямокутника знаходиться елемент поверхні, орієнтований назовні$dS = (0, dx)$, тому внесок в потік з вершини становить

$$\Phi _{top} = \int_{top}J^y (y_{top}) dx$$

Внизу назовні дає орієнтація$dS = (0, -dx)$, так

$$\Phi _{bottom} = \int_{bottom}J^y (y_{bottom}) dx$$

Використовуючи фундаментальну теорему числення, сума їх дорівнює

$$\Phi _{top} + \Phi _{bottom} = \int_{R}\frac{\partial J^y}{\partial y}dy dx$$

Додавши в аналогічні вирази для лівого і правого, отримуємо

$$\Phi = \int_{R}\left (\frac{\partial J^x}{\partial x} + \frac{\partial J^y}{\partial y} \right )dy dx$$

Але integrand - це розбіжність, яка дорівнює нулю за припущенням, так$Φ = 0$ як стверджується.

Загальна форма теореми Гаусса

Хоча координати були$x$ позначені і$y$, доказ не використовував метрику, тому результат однаково дійсний незалежно від підпису. Прямокутник міг однаково добре бути прямокутником у$1 + 1$ -вимірному просторовічасі. Узагальнення до$n$ розмірів також автоматичне, і все також проходить без змін, якщо ми замінимо вектор$J^a$ тензором, таким як$T^{ab}$, який має більше індексів - додатковий індекс$b$ просто приходить для їзди. Іноді, як і у випадку з законом Гаусса в електромагнетизмі, нас цікавлять поля, розбіжності яких не дорівнюють нулю. Теорема Гаусса тоді стає

$$\int_{S} J^a dS_a= \int_{R}\frac{\partial J^a}{\partial x^a} dv$$

де$dv$ - елемент$n$ -volume. У$3 + 1$ вимірах ми могли б використовувати координати Мінковського, щоб записати елемент$4$ -volume as$dv = dt dx dy dz$, і хоча цей вираз написано з точки зору цих конкретних координат, насправді це інваріантний Лоренц (розділ 2.5).

Малюнок$\PageIndex{2}$: Доказ теореми Гаусса для області з довільною формою.

Узагальнення до області$R$ з довільною формою, фігурою$\PageIndex{2}$, менш тривіальне. Основна ідея полягає в тому, щоб розбити область на прямокутні коробки, малюнок$\PageIndex{2}$ (1). Там, де грані двох коробок збігаються на внутрішній частині$R$, їх власні зовнішні напрямки протилежні. Тому, якщо ми додаємо потоки через поверхні всіх коробок, внески на інтер'єр скасовуються, і ми залишаємось лише зовнішніми внесками. Якби можна$R$ було розсікати точно на коробки, то це завершило б доказ, оскільки сума зовнішніх внесків була б такою ж$S$, як потік через, а ліва сторона теореми Гаусса була б добавкою над коробками, як і права сторона.

Складність виникає через те, що гладку форму, як правило, не можна побудувати з цегли, факт, який добре відомий ентузіастам Lego, які будують складні моделі зірки смерті. Ми могли б стверджувати на фізичних підставах, що жодне реальне вимірювання потоку не може залежати від зернистої структури$S$ в довільно малих масштабах, але це відчуває себе трохи незадовільним. Для порівняння, не зовсім вірно, що ділянки поверхні можна обробляти таким чином. Наприклад, якщо ми наближаємо одиницю$3$ -сферу за допомогою менших і менших коробок$6π$, межа площі поверхні становить, яка зовсім трохи перевищує площу поверхні$4π/3$ граничної поверхні.

Натомість ми явно розглядаємо непрямокутні частини на поверхні, такі як на малюнку$\PageIndex{2}$ (2). На цьому кресленні в$n = 2$ розмірах верхня частина цього шматка є приблизно лінією, і в межі, яку ми будемо розглядати, де його ширина стає нескінченно маленькою$dx$, похибка, понесена при наближенні його як лінії, буде незначною. Визначаємо вектори$dx$ і$dx ∗$ як показано на малюнку. У більш ніж двох вимірах, показаних на малюнку, ми б наблизили верхню поверхню як$(n - 1)$ -мірний паралелепіпед, охоплений векторами.$dx ∗ , dy ∗ , . . .$ Це точка, в якій використання ковектора$S_a$ окупається значним спрощенням доказу. ¹ Застосовуючи це до верхньої частини трикутника,$dS$ визначається як лінійна функція, яка приймає вектор$J$ і дає$n$ -обсяг, що охоплюється$J$ разом з$dx ∗ , . . .$

Викличте вертикальну координату на діаграмі$t$ та розгляньте внесок у$J$ часову складову потоку від$J^t$. Оскільки розмір трикутника є нескінченно малим порядком$dx$, ми можемо$J^t$ наблизитися як постійна по всьому трикутнику, при цьому виникає лише похибка порядку$dx$. (Виклавши теорему Гаусса з точки зору похідних$J$, ми неявно припустили, що вона диференційована, тому вона не може стрибати розривно.) Оскільки лінійно$dS$ залежить не тільки від векторів,$J$ але і від усіх векторів, різниця між потоком у верхній і нижній частині трикутника дорівнює пропорційній площі, що охоплюється$J$ і$dx ∗ - dx$. Але останній вектор знаходиться в$t$ напрямку, і тому площа, яку він$J^t$ охоплює при прийнятті, дорівнює приблизно нулю. Тому внесок$J^t$ в потік через трикутник дорівнює нулю. Щоб оцінити можливу похибку через наближення, ми повинні порахувати повноваження$dx$. Можлива варіація$J^t$ над трикутником є порядком$(dx)^1$. У$dS$ ковектора порядок$(dx)^{n-1}$, тому можлива похибка потоку в порядку$(dx)^n$.

Це була лише оцінка однієї частини потоку, частина внесла складова$J^t$. Однак ми отримуємо таку ж оцінку для інших частин. Наприклад, якщо ми посилаємося на два виміри на малюнку$\PageIndex{1}$ (2) як$t$ і$x$, то зміна ролей$t$ і$x$ у вищезгаданому аргументі дає ту саму оцінку помилки для внеску від$J^x$.

Це добре. Коли ми почали цей аргумент, ми були мотивовані бути обережними нашим спостереженням, що таку величину, як площа поверхні, не$R$ можна обчислити як межу площі поверхні, наближеної за допомогою коробок. Причина, по якій ми маємо цю проблему для площі поверхні, полягає в тому, що похибка в наближенні на невеликій ділянці має порядок$(dx)^{n-1}$, який є нескінченно малим того ж порядку, що і площа поверхні самого патча. Тому, коли ми масштабуємо коробки, помилка не стає маленькою порівняно із загальною площею. Але коли ми розглядаємо флюс, похибка, спричинена кожним із шматків неправильної форми біля поверхні$(dx)^n$, йде як, що є порядком$n$ -обсягу шматка. Цей обсяг йде до нуля в тій межі, де коробки потрапляють мало, і тому помилка йде в нуль також. Це встановлює узагальнення теореми Гаусса до області$R$ довільної форми.

9.3.4 Вектор енергії-імпульсу

Святкування Ейнштейна$E = mc^2$ - це особливий випадок твердження про те, що енергія-імпульс зберігається, перетворюється як чотиривекторний, і має норму,$m$ рівну масі решти. Розділ 4.4 досліджував деякі проблеми з початковою спробою Ейнштейна на доказ цього твердження, але тільки зараз ми готові їх повністю вирішити. Однією з проблем було визначення того, що ми маємо на увазі під енергетичним імпульсом системи, яка не складається з точкових частинок. Відповідь полягає в тому, що для будь-якого явища, яке несе енергетичний імпульс, ми повинні вирішити, яким чином він сприяє стрес-енергетичний тензор. Наприклад, тензор напруження-енергії електричного і магнітного полів описаний в розділі 10.6.

Малюнок$\PageIndex{3}$: Збереження інтегрованого вектора енергії-імпульсу.

З причин, розглянутих у розділі 4.4, необхідно припустити, що енергія-імпульс локально зберігається, а також, що описувана система ізольована. Локальне збереження описується властивістю нульової дивергенції тензора напруження-енергії,$\frac{\partial T^{ab}}{\partial x^a} = 0$. Як тільки ми припускаємо локальне збереження, на малюнку$\PageIndex{3}$ показано, як довести збереження інтегрованого вектора енергії-імпульсу за допомогою теореми Гаусса. Закріпіть систему відліку$o$. Оточуючи систему, зображену у вигляді темного потоку, що протікає через простор часу, малюємо коробку. Коробка обмежена на своїй минулій стороні поверхнею, яка$o$ вважає поверхнею одночасності$s_A$, а також на майбутній стороні$s_B$. Насправді не має значення, чи сторони коробки прямі або вигнуті відповідно до o. Що має значення, так це те, що оскільки система ізольована, у нас є достатньо місця, щоб між системою та сторонами коробки була область вакууму, в якій тензор напруги енергії зникає. Спостерігач$o$ каже, що в початковий час$s_A$, що відповідає, загальна кількість енергії-імпульсу в системі була

$$p_{A}^{\mu } = -\int_{s_A} T^{\mu \nu } dS_{\nu }$$

де знак мінус виникає тому, що ми$dS_{\nu }$ приймаємо точку назовні, для сумісності з теоремою Гаусса, і це робить його антипаралельним вектору швидкості$o$, що протилежно орієнтації, визначеної в рівняннях 9.2.1 та 9.2.2. В останній час у нас є

$$p_{B}^{\mu } = \int_{s_B} T^{\mu \nu } dS_{\nu }$$

зі знаком плюс, тому що напрямок назовні тепер таке ж, як напрямок$o$. Через вакуумної області немає потоку через боки коробки, а тому за теоремою Гаусса

$$p_{B}^{\mu } - p_{A}^{\mu } = 0$$

Вектор енергії-імпульсу був глобально збережений відповідно до$o$.

Рисунок$\PageIndex{4}$: Перетворення Лоренца інтегрованого вектора енергії-імпульсу.

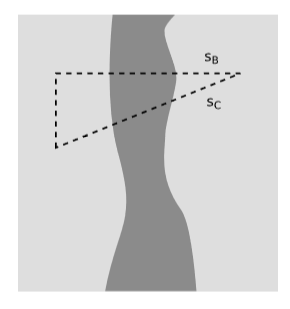
Ми також повинні показати, що інтегрований енергетичний імпульс перетворюється належним чином як чотиривектор. Щоб довести це, ми застосуємо теорему Гаусса до області, показаної на малюнку$\PageIndex{4}$, де$s_C$ є поверхня одночасності за даними якогось іншого спостерігача$o'$. Теорема Гаусса говорить нам$p_B = p_C$, що це означає, що енергія-імпульс на двох поверхнях є одним і тим же вектором в абсолютному сенсі - але це не означає, що два вектори мають однакові компоненти, що вимірюються різними спостерігачами. Спостерігач$o$ каже, що$s_B$ є поверхнею одночасності, і тому розглядає$p_B$ загальний енергетичний імпульс в певний час. Вона каже, що загальна маса енергії є$p_{B}^{\mu } o_{\mu }$ (Рівняння 9.2.1), і аналогічно для загального імпульсу в трьох просторових напрямках$s_1$$s_2$, і$s_3$ (Рівняння 9.2.2). Спостерігач$o'$, тим часом, вважає$s_C$ поверхнею одночасності і має ті ж інтерпретації для таких величин, як$p_{C}^{\mu } o'_{\mu }$. Але це лише спосіб сказати, що$p_{B}^{\mu }$ і$p_{C}^{\mu }$ пов'язані один з одним зміною основи від$(o, s_1, s_2, s_3)$ до$(o', s'_1, s'_2, s'_3)$. Така зміна основи - це саме те, що ми маємо на увазі під перетворенням Лоренца, тому інтегрований енергетичний імпульс$p$ перетворюється як чотири-вектор.

9.3.5 Кутовий момент

У розділі 8.2 ми навели фізико-математичні аргументи правдоподібності для визначення релятивістського кутового моменту як$L^{ab} = r^a p^b - r^b p^a$. Тепер ми можемо показати, що ця кількість насправді збережена. Подібно до того, як потік енергії-імпульсу$p^a$ є тензором напруги енергії$T^{ab}$, ми можемо взяти кутовий імпульс$L^{ab}$ і визначити його потік$λ^{abc} = r^a T^{bc} - r^b T^{ac}$. Спостерігач з вектором швидкості$o^c$ говорить, що щільність енергії-імпульсу є$T^{ac}o_c$ і щільність кутового моменту дорівнює$λ^{abc}o_c$. Якщо ми можемо показати, що розбіжність по відношенню до третього його індексу дорівнює нулю, то$λ$ з цього випливає, що кутовий імпульс зберігається. Розбіжність - це

$$\frac{\partial \lambda ^{abc}}{\partial x^c} = \frac{\partial }{\partial x^c} \left (r^a T^{bc} - r^b T^{ac} \right )$$

Правило продукту дає

$$\frac{\partial \lambda ^{abc}}{\partial x^c} = \delta _{c}^{a} T^{bc} + r^a \frac{\partial }{\partial x^c} T^{bc} - \delta _{c}^{b} T^{ac} - r^b \frac{\partial }{\partial x^c} T^{ac}$$

де$\delta _{j}^{i}$, звана дельтою Кронекера, визначається як$1$ якщо$i = j$ і$0$ якщо$i \neq j$. Розбіжність тензора напруження-енергія дорівнює нулю, тому другий і четвертий члени зникають, а

$$\begin{align*} \frac{\partial \lambda ^{abc}}{\partial x^c} &= \delta _{c}^{a} T^{bc} - \delta _{c}^{b} T^{ac}\\ &= T^{ba} - T^{ab} \end{align*}$$

але це нуль, тому що тензор стрес-енергії симетричний.

Посилання

¹ Ось приклад потворних ускладнень, які виникають, якщо хтось не має доступу до цієї технології. У низькотехнологічному підході в евклідовому просторі визначається елемент площі поверхні$dA = \hat{n} dA$, де одиничний вектор$\hat {n}$ спрямований назовні$\hat{n} \cdot \hat{n} = 1$. Але в сигнатурах, таких як +−−−, ми могли б мати$R$ таку область, що на деякій великій площі обмежуючої поверхні$S$ нормальний напрямок був світлоподібним. Тому було б неможливо масштабувати$\hat {n}$ так, щоб$\hat{n} \cdot \hat{n}$ було нічого, крім нуля. Як приклад того, скільки роботи потрібно вирішити такі проблеми за допомогою інструментів кам'яного віку, див. Синге, відносність: Спеціальна теорія, VIII, §6-7, де повний аргумент займає 22 сторінки.