4.3: Релятивістський імпульс

Цілі навчання

• Поясніть відносність і імпульс
• Глобальне збереження імпульсу

Вектор енергії-імпульсу

Ньютонівська механіка має два різних міри руху, кінетичну енергію та імпульс, і зв'язок між ними нелінійний, наприклад, подвоєння імпульсу вашого автомобіля в чотири рази збільшує його кінетичну енергію. Однак нерелятивістська механіка не може обробляти безмасові частинки, які завжди ультрарелятивістські. Ми побачили в розділі 4.1, що ультрарелятивістські частинки є «загальними» в тому сенсі, що вони не мають ніяких індивідуальних механічних властивостей, крім енергії та напрямку руху. Тому зв'язок між кінетичною енергією та імпульсом повинна бути лінійною для ультрарелятивістських частинок. Наприклад, подвоєння амплітуди електромагнітної хвилі в чотири рази збільшує як її енергетичну щільність, яка залежить від\(E^2\) і\(B^2\), так і її щільність імпульсу, яка йде подібно\(E×B\).

Як ми можемо зрозуміти ці енергетично-імпульсні відносини, які, здається, набувають двох абсолютно різних форм у граничних випадках дуже низьких і дуже високих швидкостей?

Перший крок - усвідомити, що оскільки маса та енергія еквівалентні, ми отримаємо більше порівняння яблук до яблук, якщо перестанемо говорити про кінетичну енергію матеріального об'єкта і розглянемо замість цього його загальну енергію Е, яка включає внесок від його маси.

Малюнок\(\PageIndex{1}\): У\(p-E\) площині безмасові частинки лежать по двох діагоналей, тоді як частинки з масою лежать праворуч.

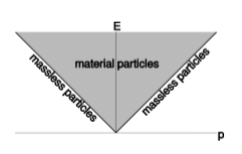
Малюнок\(\PageIndex{1}\) - це графік енергії проти імпульсу. У цьому поданні безмасові частинки, які мають\(E \propto |p|\), лежать на двох діагональних лініях, які з'єднуються біля початку. Якщо нам подобається, ми можемо підібрати одиниці такі, щоб ухили цих ліній були плюс-мінус один. Частинки матеріалу лежать над цими лініями. Наприклад, машина, що сидить на стоянці, має\(p = 0\) і\(E = m\).

Тепер що відбувається з таким графіком, коли ми переходимо на інший кадр або посилання, що знаходиться в русі щодо вихідного кадру? Безмасова частинка все одно повинна діяти як безмасова частинка, тому діагоналі просто розтягуються або стискаються по власній довжині. Трансформація, яка завжди приймає лінію до лінії, є лінійним перетворенням, і якщо перетворення між різними рамками відліку зберігає лінійність ліній\(p = E\) і\(p = -E\), то природно підозрювати, що це насправді якесь лінійне перетворення. Насправді перетворення повинно бути лінійним, оскільки збереження енергії та імпульсу передбачає додавання, і нам потрібно, щоб ці закони були дійсними у всіх системах відліку. Але тепер за тими ж міркуваннями, що і в розділі 1.3, перетворення повинно бути збереженням площі. Потім ми маємо ті ж три випадки, які слід розглянути, як на малюнку 1.1.10. Версія «Галілея» виключена, оскільки це означало б, що частинки зберігають ту саму енергію, коли ми змінюємо кадри. (Це те, що сталося б, якби\(c\) були нескінченними, щоб масовий еквівалент\(E/c^2\) даної енергії був нульовим, і тому трактувався\(E\) б чисто як маса.) Також не може бути правильною «обертальна» версія, оскільки вона не зберігає\(E = |p|\) діагоналі. Нам залишився третій випадок, який встановлює наступний естетично привабливий факт:

Енергія-імпульс - це чотиривекторний

Нехай ізольований об'єкт має імпульс і мас-енергію\(p\) і\(E\). Потім\(p-E\) площина перетворюється відповідно до точно такого ж виду перетворення Лоренца, як і\(x-t\) площина. Тобто,\((E,p_x,p_y,p_z)\) це чотиривимірний вектор точно так же, як\((t,x,y,z)\).

Це дуже бажаний результат. Якби це було неправдою, це було б як вивчити різні математичні правила для різних видів трьох векторів в ньютонівській механіці.

Єдине питання, що залишилося вирішити - чи збігається вибір одиниць, що дає інваріантні\(45\) -градусні діагоналі в\(x-t\) площині, таким же, як вибір одиниць, що дає такі діагоналі в\(p-E\) площині. Тобто нам потрібно встановити, що те,\(c\) що стосується\(x\) і\(t\) дорівнює\(c'\) необхідному для\(p\) і\(E\), тобто, що шкали швидкостей двох графіків підібрані. Це вірно, тому що в ньютонівському межі загальна\(E\) масова енергія - це, по суті, просто маса частинки, а потім\(p/E \approx p/m \approx v\). Це встановлює, що шкали швидкостей узгоджуються при малих швидкостях, що означає, що вони збігаються для всіх швидкостей, оскільки велика швидкість, навіть одна наближається\(c\), може бути побудована з багатьох малих кроків. (Це також встановлює, що показник,\(n\) визначений розділом 4.1\(1\), дорівнює заявленому.)

Припустимо, що частка знаходиться в стані спокою. Тоді він має\(p = 0\) і масу енергії,\(E\) рівної його масі\(m\). Тому внутрішній добуток його\((E,p)\) чотиривектора з самим собою дорівнює\(m^2\). Іншими словами, «величина» енергії-імпульсу чотиривектора просто дорівнює масі частинки. Якщо ми трансформуємося в іншу систему відліку, в якій\(p \neq 0\) внутрішній продукт залишається незмінним. В символах,

\[m^2 = E^2 - p^2\]

або, в одиницях з\(c \neq 1\),

\[(mc^2)^2 = E^2 - (pc)^2\]

Ми сприймаємо це як релятивістське визначення маси. Оскільки визначення - це внутрішній твір, який є скаляром, воно однакове у всіх системах відліку. (Деякі старі книги використовують застарілу конвенцію про позначення mγ як «маси», а m як «маса відпочинку».)

Вправа\(\PageIndex{1}\)

Інтерпретувати рівняння m^2 = E^2 −p^2 у випадку, коли\(m = 0\).

Високоточна перевірка цієї фундаментальної релятивістської залежності була проведена компанією Meyer et al. в 1963 році шляхом вивчення руху електронів в статичних електричних і магнітних полах. Вони визначають кількість

\[Y^2 = \frac{E^2}{m^2 + p^2}\]

які за спеціальною відносністю повинні дорівнювати\(1\). Їх результати, викладені в бічній панелі, показують відмінну згоду з теорією.

Приклад\(\PageIndex{1}\): Mass of two light waves

Нехай імпульс певної світлової хвилі буде\((p_t,p_x) = (E,E)\), і нехай інша така хвиля має імпульс\((E,-E)\). Загальний імпульс є\((2E,0)\). При цьому ця пара безмасових частинок має колективну масу\(2E\). Це приклад неадитивності релятивістської маси.

Інваріанти зіткнення

Приклад\(\PageIndex{1}\) показує, що маса не є добавкою, а також мірою «кількості речовини». Більш загально, припустимо, що ми маємо зіткнення між двома об'єктами, які можуть бути двома автомобілями або двома ядрами в прискорювачі частинок. Збереження (просторового) імпульсу диктує, що не вся енергія доступна для розбиття лобового скла або створення гамма-променів. Наприклад, марсіанин, який спостерігає за автостоянкою fender-bender через потужний телескоп, сказав би, що обидві машини їхали так само швидко, як винищувачі, через обертання землі, але це не робить удар голосніше. Щоб уникнути введення в оману цими залежними від кадру відволікаючими факторами, ми можемо зосередитися лише на величині, які є скалярами. Для зіткнення двох тіл існує три таких скаляри, які ми можемо побудувати:\(P_{1}^{2}\),\(P_{2}^{2}\), і\(P_1 \cdot P_2\). (Позначення\(a^2\) - це просто абревіатура для\(a \cdot a\).) Вони відомі як інваріанти зіткнення. Перші два з них - це просто квадратні маси окремих частинок.

Тепер розглянемо центр маси кадру, тобто кадр, в якому сумарний імпульс має нульову просторову частину. У цьому кадрі сумарний вектор енергії-імпульсу має форму\((E_{cm},0)\), відповідну масі\(M = E_{cm}\). Вся ця енергія доступна для того, щоб зробити чубок. Якби ми стикалися частинки в прискорювачі, щоб виробляти нові частинки, це зіткнення було б ледь достатньо енергії для створення однієї частинки маси\(M\), якби дві вхідні частинки були знищені в процесі. Цей центр енергії мас може бути виражений в терміні інваріантів зіткнення як

\[\begin{align} M^2 &= (P_1 + P_2)^2 + P_{1}^{2} + P_{2}^{2} + 2P_1 \cdot P_2 \\[5pt] &= m_{1}^{2} + m_{2}^{2} + 2P_1 \cdot P_2 \end{align}\]

Це нелінійний зв'язок, і третій інваріант зіткнення\(P_1 \cdot P_2\) говорить нам про те, як нелінійність відтворюється на основі відносних напрямків руху. Два вектори імпульсу є як тимчасовими, так і спрямованими на майбутнє, тому зворотна рівність трикутника (розділ 1.5) ми маємо

\[M \geq m_1 + m_2\]

Деякі приклади, що включають імпульс

Приклад\(\PageIndex{2}\): Finding velocity given energy and momentum

Якщо ми знаємо, що частинка має масову енергію\(E\) та імпульс\(p\) (що також передбачає знання її маси m), яка її швидкість?

Рішення

У кадрі спокою частинки вона має світову лінію, яка вказує прямо на діаграму просторового часу, а її вектор імпульсу\(p\) також вказує на\(p-E\) площину. Оскільки вектори зміщення та вектори імпульсу трансформуються за тими ж правилами, цей паралелізм буде зберігатися і в інших кадрах. Тому в довільно обраному кадрі вектор\(p = (E,p)\) лежить уздовж лінії, зворотний нахил якої\(v = p/E\) дає швидкість.

Як перевірку нашого результату ми дивимося на його обмежуючу поведінку. У ньютонівському межі\(E\) масова енергія майже все пов'язано з масою, тому ми маємо\(v \approx p/m\), Ньютонівський результат. У протилежній межі ультрарелятивістського руху\(E \gg m\), при, визначення маси\(m^2 = E^2 - p^2\) дає\(E \approx |p|\), і ми маємо\(|v| \approx 1\), що теж правильно.

Приклад\(\PageIndex{3}\): Light rays don’t interact

Ми спостерігаємо, що коли два промені світла перетинаються, вони продовжують один через одного, не підстрибуючи, як матеріальні об'єкти. Така поведінка випливає безпосередньо із збереження енергії-імпульсу.

Будь-які два вектори можуть міститися в одній площині, тому ми можемо вибрати наші координати так, щоб обидва промені зникли\(p_z\). Вибравши стан руху нашої системи координат відповідним чином, ми також можемо зробити так\(p_y = 0\), щоб зіткнення відбувалося вздовж однієї лінії, паралельної\(x\) -осі. Оскільки тільки\(p_x\) є ненульовим, ми пишемо його просто як\(p\). В отриманої\(p-E\) площині є дві можливості: або промені обидва лежать по одній діагоналі, або вони лежать по різній діагоналі. Якщо вони лежать по одній діагоналі, то зіткнення бути не може, тому що обидва променя рухаються в одному напрямку з однаковою швидкістю\(c\), а задній ніколи не наздожене провідний.

Тепер припустимо, що вони лежать уздовж різних діагоналей. Ми додаємо їх вектори енергії-імпульсу, щоб отримати їх сумарний енергетичний імпульс, який буде лежати в сірій області фігури\(\PageIndex{1}\). Тобто пара світлових променів, прийнятих як єдина система, діють ніби як матеріальний об'єкт з ненульовою масою. За допомогою перетворення Лоренца ми завжди можемо знайти кадр, в якому цей сумарний вектор енергії-імпульсу лежить уздовж\(E\) осі. Це кадр, в якому моменти двох променів скасовуються, і ми маємо симетричне лобове зіткнення між двома променями однакової енергії. Це кадр «центру маси», хоча жоден об'єкт не має маси в індивідуальному порядку. Для зручності припустимо, що система\(x-y-z\) координат була підібрана так, щоб її початок перебував в спокої в цьому кадрі.

Оскільки зіткнення відбувається вздовж\(x\) -осі, по симетрії неможливо, щоб промені після зіткнення відходили від\(x\) -осі; бо якби вони це зробили, то не було б нічого, щоб визначити орієнтацію площини, в якій вони виникли. ¹ Тому ми виправдані, продовжуючи використовувати ту ж\(p_x-E\) площину для аналізу чотирьох векторів променів після зіткнення.

Приклад\(\PageIndex{4}\): Compton scattering

Малюнок\(\PageIndex{2}\): 1. Край Комптона лежить на енергії, осадженої гамма-променями, які розсіюються на 180 градусів від електрона. Зіткнення в рамці лабораторії. Те ж саме зіткнення в центрі маси кадру.

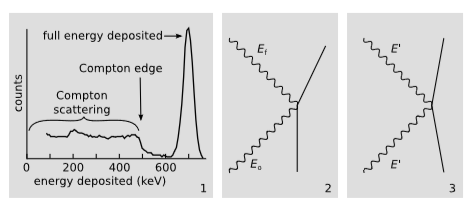
Рисунок\(\PageIndex{2}\) (1) являє собою гістограму гамма-променів, випромінюваних\(^{137}\textrm{Cs}\) джерелом і записаних сцинтиляційним детектором NaI. Цей тип детектора, на відміну від лічильника Гейгера-Мюллера, дає імпульс, висота якого пропорційна енергії випромінювання. Близько половини гамма-променів роблять те, що ми хотіли б, щоб вони робили в детекторі: вони відкладають повну енергію\(662\: keV\) в детекторі, в результаті чого на гістограмі з'являється помітний пік. Інша половина, однак, взаємодіє через процес, який називається розсіюванням Комптона, в якому вони стикаються з одним з електронів, але виходять із зіткнення, зберігаючи частину своєї енергії, за допомогою якої вони можуть втекти від детектора. Кількість енергії, що відкладається в детекторі, залежить виключно від кінематики зіткнення більярдної кулі, і може бути визначена за збереженням енергії-імпульсу на основі кута розсіювання. Пряме розсіювання в\(0\) градусах взагалі не взаємодія, і не відкладає енергії, в той час як розсіювання в\(180\) градусах відкладає максимальну енергію, можливу, якщо єдиною взаємодією всередині детектора є єдине розсіювання Комптона. Ми розберемо\(180\) -градусне розсіювання, оскільки його можна вирішити в\(1+1\) розмірах.

На малюнку\(\PageIndex{2}\) (2) показано зіткнення в лабораторному кадрі, де електрон спочатку знаходиться в стані спокою. Як це прийнято в цьому типі діаграми, світова лінія фотона відображається як хитка лінія; хитання є лише прикрасою, а фактична світова лінія складається з двох відрізків лінії. Фотон надходить в детектор з повною енергією\(E_o = 662\: keV\) і йде з меншою енергією\(E_f\). Різниця\(E_o - E_f\) полягає в тому, що детектор буде вимірювати, сприяючи підрахунку на край Комптона. У лабораторному кадрі загальний початковий вектор імпульсу - це часовий компонент\(p = (E_o + m,E_o)\), який представляє загальну масову енергію. Оскільки фотон безмасовий, його імпульс\(p_x = E_o\) дорівнює його енергії.

\(v\)Дозволяти швидкість центру маси кадру\(e/3\), по відношенню до лабораторії кадру. Використовуючи результат прикладу\(\PageIndex{2}\), знаходимо

\[v = \frac{E_o}{E_o + m}\]

Щоб полегшити написання, ми визначаємо

\[\alpha = E_o/m\]

так що

\[v = \frac{\alpha }{1 + \alpha }\]

Перетворення з лабораторного кадру в cm. кадр Допплер зміщує енергію падаючого фотона вниз до

\[E' = D(-v)E_o\]

Зіткнення змінює просторову частину вектора енергії-імпульсу фотона, залишаючи його енергію колишньою. Трансформація назад в лабораторний кадр дає

\[E_f = D(-v)E' = D(-v)^2E_o = \frac{E_o}{1 + 2\alpha }\]

(Це також можна переписати, використовуючи квантово-механічне відношення,\(E = hc/λ\) щоб надати компактну форму\(λ_f - λ_o = 2hc/m\).) Кінцевим результатом для енергії краю Комптона є

\[E_o - E_f = \frac{E_o}{1 + \tfrac{1}{2\alpha }}\]

в хорошому узгодженні з фігурою\(\PageIndex{2}\).

Приклад\(\PageIndex{5}\): Pair production requires matter

Приклад 4.2.1 обговорював анігіляцію електрона і позитрона в два гамма-промені, що є прикладом перетворення речовини в чисту енергію. Протилежний приклад - парне виробництво, процес, при якому гамма-промінь зникає, а його енергія йде на створення електрона і позитрона.

Виробництво пари не може відбуватися у вакуумі. Наприклад, гамма-промені з далеких чорних дір можуть проходити через порожній простір тисячоліттями, перш ніж їх виявляти на землі, і вони не перетворюються на електрон-позитронні пари, перш ніж вони зможуть потрапити сюди. Парне виробництво може відбуватися тільки при наявності матерії. Коли свинець використовується як захист від гамма-променів, одним із способів зупинки гамма-променів у відведенні є проходження парного виробництва.

Щоб зрозуміти, чому виробництво пари заборонено у вакуумі, розглянемо процес в системі відліку, в якому електрон-позитронна пара має нульовий сумарний імпульс. У цьому кадрі гамма-промінь мав би мати нульовий імпульс, але гамма-промінь з нульовим імпульсом також повинен мати нульову енергію. Це означає, що збереження вектора імпульсу було порушено: часоподібна складова імпульсу - це мас-енергія, і вона збільшилася з\(0\) в початковому стані до хоча б\(2mc^2\) в кінцевому стані.

Безмасові частинки подорожують\(c\)

Безмасові частинки завжди подорожують на\(c(= 1)\). Бо припустимо, що безмасова частка мала\(|v| < 1\) в кадрі якогось спостерігача. Тоді якийсь інший спостерігач міг перебувати в спокої щодо частинки. У такому кадрі імпульс частинки\(p\) дорівнює нулю по симетрії, так як для неї немає бажаного напрямку. Тоді також\(E^2 = p^2 + m^2\) дорівнює нулю, тому весь вектор енергії-імпульсу частинки дорівнює нулю. Але вектор, який зникає в одному кадрі, також зникає в кожному іншому кадрі. Це означає, що ми говоримо про частинку, яка не може зазнати розсіювання, випромінювання або поглинання, і тому її неможливо виявити будь-яким експериментом. Це фізично неприйнятно, тому що ми не вважаємо явища (наприклад, невидимі феї) представляють фізичний інтерес, якщо вони не виявляються навіть в принципі.

Як щодо випадку матеріальної частинки, тобто тієї, що має масу? Оскільки у нас вже є рівняння\(E = mγ\) енергії матеріальної частинки з точки зору її швидкості, ми можемо знайти подібне рівняння для імпульсу,

\[\begin{align} p &= \sqrt{E^2 - m^2} \nonumber \\[5pt] &= m\sqrt{\gamma ^2 - 1} \nonumber \\[5pt] &= m\sqrt{\frac{1}{1 - v^2} - 1} \nonumber \\[5pt] &= m\gamma v \label{rel momentum} \end{align}\]

(Відношення, яке корисне в своєму власному праві, і було перевірено експериментальним шляхом, рис.\(\PageIndex{3}\)).

Малюнок\(\PageIndex{3}\): Два ранніх високоточних випробування релятивістського рівняння\(p = mγv\) для імпульсу матеріальної частинки. Графік,\(p/m\) а не\(p\) дозволяє розміщувати дані для електронів та протонів на одному графіку. Дуже малі смуги помилок для точки даних з Зрєлова представлені висотою чорного прямокутника.

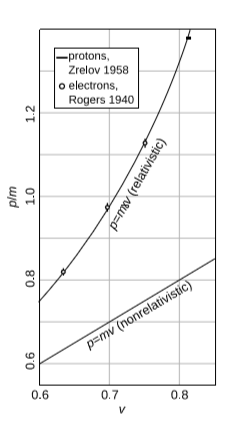
Коли матеріальна частинка стає все ближче і ближче до\(c\), її імпульс наближається до нескінченності, так що для досягнення цього потрібна нескінченна сила\(c\).

Підсумовуючи, безмасові частинки завжди рухаються\(v = c\), тоді як масивні завжди рухаються\(v < c\).

Зауважте, що рівняння\(p = mγv\) (Equation\ ref {rel momentum}) не є достатньо загальним, щоб служити визначенням імпульсу, оскільки воно стає невизначеною формою в межі\(m \rightarrow 0\).

Приклад\(\PageIndex{6}\): No half-life for massless particles

Приклад\(\PageIndex{7}\): Constraints on polarization

Ми спостерігаємо, що електромагнітні хвилі завжди поляризовані поперечно, ніколи поздовжньо. Таке обмеження може стосуватися тільки хвилі, яка поширюється при\(c\). Якби він застосовувався до хвилі, яка поширювалася менше\(c\), ніж, ми могли б перейти в систему відліку, в якій хвиля була в стані спокою. У цьому кадрі всі напрямки в просторі були б рівнозначними, і не було б можливості вирішити, які напрямки поляризації повинні бути дозволені.

Докази того, які частинки є безмасовими

Які з основних частинок безмасові, а які ні? Це можна визначити лише емпіричним шляхом, і у нас є принаймні один приклад, нейтрино, який раніше вважався безмасовим, але тепер вважається масивним. Детальніше про нейтрино див. Розділ 4.7. У цьому розділі ми обговорюємо межі на маси фотона і гравітона. ⁵ Ми опускаємо обговорення глюона, яке ускладнювалося б тим, що глюон ніколи не спостерігається як вільна частинка або як класичне поле. Цей розділ можна пропустити без втрати безперервності.

Деякі читачі можуть вигукнути в цей момент, що, звичайно, фотони повинні бути безмасовими, тому що світло повинен подорожувати зі швидкістю світла. Але з вищевикладеного викладу повинно бути зрозуміло, що\(c\) в відносності слід інтерпретувати не як швидкість світла, а як своєрідний коефіцієнт перетворення між простором і часом. Якщо фотони мають невелику, але не зникаючу масу, відносність не має кола, що рухається через його серце.

Якщо ми хочемо перевірити, чи є фотон безмасовим, найпростішою технікою, здавалося б, є вимірювання часу польоту, коли він проходить певну відстань, і подивитися, чи йде він повільніше, ніж\(c\). Тут виникають труднощі, оскільки наші методи вимірювання великих відстаней, наприклад, GPS, зазвичай припускають, що світло рухається на\(c\). Однак якщо фотон має деяку масу, то його швидкість повинна залежати від його енергії, тому ми можемо замість цього перевірити, чи залежить швидкість фотона від його енергії. З квантової механіки це пов'язано з його частотою\(E = hf\), тому ми по суті перевіряємо, чи залежить швидкість світла у вакуумі від частоти. В даний час найкращі експериментальні випробування інваріантності швидкості світла по відношенню до довжини хвилі походять від астрономічних спостережень гамма-сплеску, які є раптовими виливами високоенергетичних фотонів, які, як вважають, походять від вибуху наднової в іншій галактиці. Одне з таких спостережень, в 2009 році ⁶ зібрали фотони з такого сплеску, тривалістю в\(2\) секунди, що свідчить про те, що час поширення всіх фотонів відрізнялося не більше ніж на\(2\) секунди із загального часу польоту близько десяти мільярдів років, або приблизно на одну частину в \(10^{17}\)!

Малюнок\(\PageIndex{4}\): Концепція художника про гамма-сплеск, що виникає в результаті вибуху наднової.

Виявляється, однак, що обмеження на масу фотона, накладені часом польотних вимірювань, можна поліпшити на багато порядків за допомогою інших методів. У стандартній моделі фізики частинок сили передаються шляхом обміну частинок. Ми зосередимося тут на статичних силах. Електростатична сила передається шляхом обміну фотонами, а статична гравітаційна сила - шляхом обміну гравітонами. Гравітація не є частиною стандартної моделі фізики частинок, і окремі гравітони не можуть бути безпосередньо виявлені жодною передбачуваною технологією ⁷, але є фундаментальні причини вважати, що вони повинні існувати, і в будь-якому випадку наша дискусія математично ідентична для гравітації і електромагнетизм. Тому ми обговоримо електромагнітні поля, а потім відзначимо відповідні результати для гравітації.

Якщо уявити поле, що оточує нерухомий точковий заряд, як рій фотонів, то перше питання, яке виникає перед нами, - що таке джерело енергії, необхідної для їх створення. Стандартний аргумент, що розмахує рукою, виглядає наступним чином. Крім звичайної моментно-енергетичної форми принципу невизначеності Гейзенберга\(\Delta p \Delta x \overset{> }{\sim } h\), існує енергетично-часова форма\(\Delta E \Delta t \overset{> }{\sim } h\). Це виглядає очевидним за аналогією, коли ми вважаємо, що релятивістично енергія та імпульс є різними частинами чотири-вектора енергії-імпульсу, а також для часу та положення. Ми можемо інтерпретувати це, щоб означати, що можна протягом коротких періодів часу обдурити закон збереження енергії. Ми можемо вкрасти трохи енергії, але потім негайно повернути її назад, якщо тривалість кредиту не більше, ніж приблизно\(t \sim h/E\). За цей час віртуальна частка може пройти відстань не більше\(\sim hc/E\). Тепер для безмасової частинки ця енергія може бути як завгодно маленькою, тому сила може досягати довільно великих відстаней. Але для масивної частинки ми маємо релятивістське відношення\(E^2 - p^2 = m^2\), яке вимагає\(E ≥ m\), або\(E ≥ mc^2\) в одиницях СІ. Ця мінімальна енергія відповідає максимальному діапазону\(\sim h/mc\). Загалом, ми очікуємо, що поле, яке несе масивна частинка, швидше відвалиться з відстанню, ніж поле безмасової частинки, і ми очікуємо, що це падіння буде якось параметризовано шкалою довжини\(h/mc\).

Як би ми очікували, що це відіграє в класичній теорії електромагнітних полів?

Малюнок\(\PageIndex{5}\): Лінії поля точкового заряду. Спостереження в межах невеликої області, зазначеної коробкою, дозволяють визначити, наскільки далеко знаходиться заряд 2. Польові лінії нескінченної пластини конденсатора, згідно зі стандартним електромагнетизмом. Спостереження всередині коробки не дають інформації про те, наскільки далеко знаходиться заряд 3. Порушення закону Гаусса.

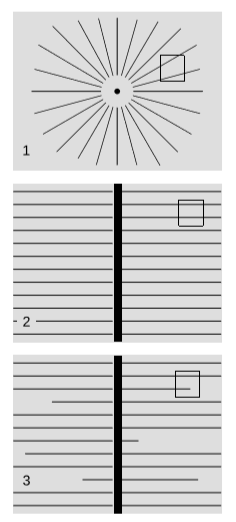
Розглянемо точковий заряд, цифра\(\PageIndex{5}\) (1). Лінії поля є прямими, і вони поширюються в усіх напрямках, тому шляхом спостережень будь-якої області простору ми можемо простежити лінії назад, щоб побачити, де вони б перетиналися. Саме так далеко він знаходиться від нашого регіону космосу до заряду. Це своєрідне вимірювання паралакса. У випадку з гравітацією це саме те, що зробив Ератосфен для того, щоб виміряти радіус землі.

Але тепер давайте розглянемо випадок нескінченної, плоскої пластини конденсатора з деяким зарядом на ній, малюнок\(\PageIndex{5}\) (2). Лінії полів не поширюються, тому метод паралакса не працює. Якщо досліджувати поле в якомусь невеликому ділянці простору, то не повинно бути можливості визначити відстань до пластини конденсатора. Якщо ми віримо в закон Гаусса, то рішення просте: поле постійне як за величиною, так і за напрямком, тому, хоча воно говорить нам напрямок найближчої точки на тарілці, воно нічого не говорить нам про відстань до цієї точки.

Але якщо фотон масивний, ми очікуємо, що поля будуть падати швидше з відстанню, ніж вони були б відповідно до стандартної теорії. У цьому прикладі стандартна теорія говорить, що поле зовсім не зменшується з відстанню, тому для масивного фотона ми очікуємо, що він дійсно відпаде. Це порушить закон Гаусса, але ми все ж очікуємо, що відстань до пластини не буде визначено дослідженням невеликої області простору: якщо рівняння поля лінійні, то поле з заданою напруженістю могло бути від розташованої поруч пластини конденсатора з малою щільністю заряду, або більш віддаленої з більше заряду.

Якщо ми готові порушити закон Гаусса, то ми можемо просто закінчити лінії полів у порожньому просторі, цифра\(\PageIndex{1}\) (3), і це призведе до зменшення напруженості поля. Коли ми проходимо невелику відстань\(dx\), віддаляючись від плити, деяка частка ліній поля повинна закінчуватися, що призводить до відповідного дробового\(dE/E\) зменшення напруженості поля. Співвідношення\(\frac{\tfrac{dE}{E}}{dx}\) повинно бути постійним, і це може статися тільки в тому випадку, якщо у нас\(µ\) є\(E \propto e^{-\mu x}\), де константа з одиницями зворотної довжини. (На іншій стороні пластини, де\(x\) негативна, ми маємо\(+µx\) всередині експоненціальну.) З причин, розглянутих вище, ми насправді очікуємо, що\(µ\) дорівнює\(mc/h\) множиться на безодиничну константу одиниці порядку. Насправді, можна показати, що безодинична константа є коефіцієнтом\(2π\), тому\(µ\) просто маса, виражена в одиницях, де обидва\(c\) і\(\hbar\) рівні\(1\).

Оскільки поле пластини конденсатора дорівнює накладенню полів всіх розподілених на ній рівномірно зарядів, то наш результат того, що поле конденсатора відпадає певним чином, говорить нам щось відповідне про поле точкового заряду. Ми очікуємо, що поле точкового\(q\) заряду

\[E = kq\frac{e^{-\mu r}}{r^2}\]

де закон Кулона відновлюється у справі\(µ = 0\). Ця форма спочатку була виведена Юкавою для ядерних сил, які дійсно мають кінцевий діапазон.

Тепер у нас є надзвичайно чутливий спосіб встановлення обмеження на маси фотона та гравітону. Навіть якщо\(µ\) він дуже малий, ми можемо робити спостереження на дуже великих масштабах відстані, і статичні сили повинні падати експоненціально. У випадку гравітаційних сил ми спостерігаємо, що гравітація діє, не виявляючи загасання в стилі Юкави, на масштабах, порівнянних з розміром спостережуваного Всесвіту, на порядку мільярдів світлових років. Це відповідає обмеженню маси гравітону\(\sim 10^{-69}\: kg\) - безумовно, найменшого масового масштабу, який коли-небудь досліджувався людьми! Вимірювання магнітного поля Юпітера космічним зондом Pioneer 10 обмежують масу фотона не більше, ніж приблизно\(8×10{-52}\: kg\), що майже так само вражає.

Хоча сьогоднішні найжорсткіші межі - це сонячна система та космологічні вимірювання, історично були проведені дуже точні настільні експерименти. Лабораторні експерименти завжди бажані в таких випадках, оскільки умови можна контролювати, а експерименти можна повторити.

Немає глобального збереження енергії-імпульсу в загальній теорії відносності

Якщо ви читаєте главу 2, ви знаєте, що відмінність між спеціальною та загальною відносністю визначається плосністю простору-часу, і що площинність, в свою чергу, визначається незалежністю шляху паралельного транспорту. Тоді як енергія є скаляром в ньютонівській механіці, в теорії відносності це часова складова вектора. Тому випливає, що в загальній теорії відносності ми не повинні очікувати глобального збереження енергії. Для закону збереження є твердження, що коли ми складаємо певну величину, загальна має постійне значення. Але якщо просторово-час вигнутий, то немає природного, однозначно визначеного способу порівняння векторів, які визначені в різних місцях просторучасу. Ми могли б паралельно транспортувати один на інший, але результат буде залежати від шляху, по якому ми вирішили його транспортувати. З аналогічних причин не варто очікувати глобального збереження імпульсу.

Це відповідь на часто задається питання про космологію. З 1998 року ми знаємо, що розширення Всесвіту прискорюється, а не сповільнюється, як ми очікували через гравітаційне тяжіння. Що є джерелом постійно зростаючої кінетичної енергії всіх цих галактик? Питання передбачає, що енергія повинна зберігатися в космологічних масштабах, але це не так.

Тим не менш, загальна відносність зводиться до спеціальної відносності на шкалах, досить малих, щоб зробити ефекти кривизни незначними. Тому все ще справедливо очікувати збереження енергії та імпульсу, щоб утримуватися локально, як передбачається, наприклад, в аналізі розсіювання Комптона на прикладі\(\PageIndex{4}\), і перевірено в незліченних експериментах.

Посилання

¹ У квантовій механіці тут є лазівка. Квантова механіка допускає певні види випадковості, так що симетрія може бути порушена, дозволяючи відходять променям спостерігатися в площині з деякою випадковою орієнтацією.

² Тут є друга лазівка, яка полягає в тому, що промінь світла насправді є хвилею, а хвиля має інші властивості, крім енергії та імпульсу. Він має довжину хвилі, а деякі хвилі також мають властивість, звану поляризацією. Як механічної аналогії для поляризації розглянемо натягнуту тугу мотузку. Бічні коливання можуть поширюватися уздовж мотузки, і ці коливання можуть виникати в будь-якій площині, яка збігається з мотузкою. Орієнтація цієї площини називається поляризацією хвилі. Повертаючись до випадку зіткнення світлових променів, можна мати нетривіальні зіткнення в тому сенсі, що промені могли впливати один на одного довжини хвиль і поляризації. Хоча це насправді не відбувається з неквантово-механічними світловими хвилями, це може статися з іншими типами хвиль; див., наприклад, Hu et al., arxiv.org/abs/hep-ph/9502276, малюнок 2. Назва прикладу 4.3.3 є дійсним лише в тому випадку, якщо «промінь» вважається чимось, що не вистачає хвильової структури. Хвильова природа світла не проявляється в повсякденному житті від спостережень за допомогою таких апаратів, як ліхтарі, дзеркала та окуляри, тому ми очікуємо, що результат буде триматися за цих обставин, і це відбувається. Наприклад, промені ліхтарів проходять через один пильовик, не взаємодіючи.

³ Див. Фіоре і Моданезе, arxiv.org/abs/hep-th/9508018 та http://physics.stackexchange.com/questions/12488/ розпад безмасових частинок. Якщо такий процес дійсно існує, то інваріантність Лоренца вимагає, щоб його часова шкала була пропорційною енергії частинки. Можна стверджувати, що глюони, які є безмасовими, насправді зазнають розпаду на менш енергійні глюони, але інтерпретація неоднозначна, оскільки ми ніколи не спостерігаємо глюони як вільні частинки, тому ми не можемо просто захопити один у коробці і спостерігати, як він гримить всередині, поки він не розпадається.

⁴ Для поглибленого огляду цієї теми див. Голдхабер і Ніето, «Межі маси фотонів та гравітонів» http://arxiv.org/abs/0809.1003.

⁵ http://arxiv.org/abs/0908.1832

⁶ Ротман і Боун, «Чи можна виявити гравітони? ,» http://arxiv.org/ абс/гр-qc/0601043