Skip to main content
LibreTexts - Ukrayinska

29.2: Ранній атом

  1. Last updated
  2. Save as PDF
  • Page ID
    74894

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    навчальні цілі

    • Обговорити експерименти, які привели до відкриття електрона і ядра

    Хоча спочатку розглядалася як частинка, яку неможливо розрізати на більш дрібні частинки, сучасне наукове використання позначає атом як складений з різних субатомних частинок. Складовими частинками атома (кожен виявлений самостійно) є: електрон, протон і нейтрон. (Атом водню-1, однак, не має нейтронів, а позитивний іон водню не має електронів.)

    зображення

    Класична атомна модель: атомна модель до появи квантової механіки.

    Електрон

    Німецький фізик Йоганн Вільгельм Хітторф взявся за вивчення електропровідності в розріджених газах. У 1869 році він виявив світіння, що випромінюється від катода, яке збільшувалося в розмірах зі зниженням тиску газу. У 1896 році британський фізик Джей Джей Томсон провів експерименти, що демонструють, що катодні промені були унікальними частинками, а не хвилями, атомами або молекулами, як вважалося раніше. Томсон зробив хороші оцінки як заряду ee, так і маси mm, виявивши, що електронно-променеві частинки (які він назвав «тільцями») мали, мабуть, тисячну масу водню, найменш масивного відомого іона. Він показав, що їх відношення заряду до маси (e/m) не залежить від катодного матеріалу. (На рис. 1 показаний промінь відхилених електронів.)

    зображення

    Електронний промінь: Пучок електронів, відхилений по колу магнітним полем.

    Протон

    У 1917 році (в експериментах, повідомлених в 1919 році) Резерфорд довів, що водневе ядро присутнє в інших ядрах, результат зазвичай описується як відкриття протона. Раніше Резерфорд навчився створювати ядра водню як вид випромінювання, що утворюється як вихід впливу альфа-частинок на газ водню; ці ядра були визнані за їх унікальною ознакою проникнення в повітря та їх появою в сцинтиляційних детекторах. Ці експерименти почалися, коли Резерфорд помітив, що коли альфа-частинки були вистрілені в повітря (переважно азот), його сцинтиляційні детектори відображали підписи типових ядер водню як продукту. Після експериментів Резерфорд простежив реакцію на азот у повітрі і виявив, що ефект був більшим, коли альфи вироблялися в чистий газ азоту. Резерфорд визначив, що єдиним можливим джерелом цього водню був азот, а тому азот повинен містити ядра водню. Одне ядро водню було збите під впливом альфа-частинки, виробляючи кисень-17 в процесі. Це була перша повідомила ядерна реакція,\(14 \mathrm { N } + \alpha \rightarrow 17 \mathrm { O } + \mathrm { p }\).

    Нейтронний

    У 1920 році Ернест Резерфорд задумав можливе існування нейтрона. Зокрема, Резерфорд дослідив виявлену нерівність між атомним номером атома та його атомною масою. Його поясненням цьому стало існування нейтрально зарядженої частинки всередині атомного ядра. Він вважав нейтрон нейтральним двійником, що складається з електрона, що обертається навколо протона. У 1932 році Джеймс Чедвік показав незаряджені частинки в використовуваному ним випромінюванні. Ці частинки мали подібну масу, як протони, але не мали таких же характеристик, як протони. Чедвік слідував деяким прогнозам Резерфорда, першим, хто працював у цій тоді невідомій галузі.

    Ранні моделі атома

    Дальтон вважав, що ця матерія складається з дискретних одиниць, які називаються атомами - неподільні, кінцеві частинки речовини.

    навчальні цілі

    • Охарактеризуйте постулати атомної теорії Дальтона та атомних теорій давньогрецьких філософів

    Атом - це основна одиниця речовини, яка складається з щільного центрального ядра, оточеного хмарою негативно заряджених електронів. Атомне ядро містить суміш позитивно заряджених протонів і електрично нейтральних нейтронів (за винятком випадку водню-1, який є єдиним стабільним нуклідом без нейтронів). Електрони атома пов'язані з ядром електромагнітною силою. У нас зараз детальна (і точна) модель атома, але на те, щоб придумати правильну відповідь, знадобилося багато часу.

    зображення

    Ілюстрація атома гелію: Це ілюстрація атома гелію, що зображує ядро (рожеве) та розподіл електронної хмари (чорний). Ядро (вгорі праворуч) у гелію-4 насправді сферично симетрично і дуже нагадує електронну хмару, хоча для більш складних ядер це не завжди так. Чорною смугою є один ангстрем (10−1010−10 м, або 100 вечора).

    Люди давно спекулюють про будову матерії і існування атомів. Найбільш ранні значущі ідеї вижити є у стародавніх греків в п'ятому столітті до нашої ери, особливо від філософів Левкіппа і Демокріта. (Є деякі докази того, що філософи як в Індії, так і в Китаї робили подібні міркування приблизно в той же час.) Вони розглядали питання про те, чи можна без обмежень розділити речовину на все менші шматки. На це питання є лише кілька можливих відповідей. Одна з них полягає в тому, що можливий нескінченно малий підрозділ. Іншим є те, що, зокрема, вважав Демокріт — що існує найменша одиниця, яку неможливо розділити далі. Демокріт назвав це атомом. Тепер ми знаємо, що самі атоми можна поділити, але їх ідентичність руйнується в процесі, тому греки були правильними у відношенні. Греки також відчували, що атоми знаходяться в постійному русі, ще одне правильне поняття.

    Греки та інші спекулювали про властивості атомів, припускаючи, що існувало лише кілька типів і що вся матерія формувалася як різні комбінації цих типів. Знаменита пропозиція про те, що основними елементами були земля, повітря, вогонь та вода, було блискучим, але неправильним. Греки визначили найпоширеніші приклади чотирьох станів речовини (твердого, газового, плазмового та рідкого), а не основних хімічних елементів. Минуло більше 2000 років, перш ніж можна було провести спостереження за допомогою обладнання, здатного виявити справжню природу атомів.

    Протягом століть були зроблені відкриття щодо властивостей речовин і їх хімічних реакцій. Були визнані певні систематичні ознаки, але подібність між загальними і рідкісними елементами призвела до зусиль перетворити їх (свинець у золото, зокрема) для отримання фінансової вигоди. Таємниця була звичайною справою. Алхіміки виявили і заново відкрили багато фактів, але не зробили їх широко доступними. У міру закінчення середньовіччя практика алхімії поступово згасала, і виникла наука про хімію. Більше не можна було і не вважалося бажаним зберігати відкриття в таємниці. Колективні знання росли, і до початку 19-го століття був добре встановлений важливий факт: маси реагентів в конкретних хімічних реакціях завжди мають певне масове співвідношення. Це дуже вагомі непрямі докази того, що існують основні одиниці (атоми і молекули), які мають такі ж масові співвідношення. Більшу частину цієї роботи зробив англійський хімік Джон Далтон (1766-1844) зі значним внеском італійського фізика Амедео Авогадро (1776-1856). Саме Авогадро розробив ідею фіксованого числа атомів і молекул в молі. Цей спеціальний номер називається номером Авогадро в його честь (\(\mathrm{6.022⋅1023}\)).

    Дальтон вважав, що матерія складається з дискретних одиниць, званих атомами, на відміну від застарілого поняття, що матерія може бути розділена на будь-яку довільно малу кількість. Він також вважав, що атоми є неподільними, кінцевими частинками речовини. Однак це повір'я було скасовано ближче до кінця 19-го століття Томсоном, з його відкриттям електронів.

    Вступ до історії атомної теорії - Вступ: Резерфорд, Томсон, електрони, ядра та сливи. Я не маю на увазі бути бором, але чи вважаєте ви, що пудинг повинен мати певну роль у серйозному науковому дослідженні?

    Модель Томсона

    Томсон запропонував, що атом складається з електронів, оточених супом позитивного заряду, щоб збалансувати негативні заряди електронів.

    навчальні цілі

    • Охарактеризуйте модель атома, запропоновану Дж. Томсоном.

    Дж. Томсон, який відкрив електрон в 1897 році, запропонував модель атома сливового пудингу в 1904 році до відкриття атомного ядра, щоб включити електрон в атомну модель. У моделі Томсона атом складається з електронів (які Томсон все ще називав «корпускулами», хоча Джей Стоні запропонував атоми електрики називати електронами в 1894 році), оточених супом позитивного заряду, щоб збалансувати негативні заряди електронів, як негативно заряджені «сливи», оточені позитивно заряджається «пудинг». Вважалося, що електрони (як ми їх знаємо сьогодні) розташовуються по всьому атому в обертових кільцях. У цій моделі також іноді описувалося, що атом має «хмару» позитивного заряду.

    зображення

    Модель атома сливового пудингу: Схематичне представлення моделі атома сливового пудингу; в математичній моделі Томсона «тільця» (сучасною мовою, електрони) були розташовані невипадково, у обертових кільцях.

    З цією моделлю Томсон відмовився від своєї більш ранньої гіпотези «небулярного атома», в якій атом складався з нематеріальних вихорів. Тепер принаймні частина атома повинна була складатися з твердих негативних тілець Томсона, хоча решта позитивно зарядженої частини атома залишалася дещо туманною і погано визначеною.

    Модель Томсона 1904 року була спростована експериментом із золотої фольги 1909 року, проведеним Гансом Гейгером та Ернестом Марсденом. Цей експеримент із золотою фольгою був інтерпретований Ернестом Резерфордом в 1911 році, щоб припустити, що існує дуже маленьке ядро атома, яке містить дуже високий позитивний заряд (у випадку з золотом, достатньо, щоб збалансувати колективний негативний заряд близько 100 електронів). Його висновки змусили його запропонувати Резерфордську модель атома.

    Вступ до історії атомної теорії - Модель Томсона: Резерфорд, Томсон, електрони, ядра та сливи. Я не маю на увазі бути бором, але чи вважаєте ви, що пудинг повинен мати певну роль у серйозному науковому дослідженні?

    Модель Резерфорда

    Резерфорд підтвердив, що атом мав концентрований центр позитивного заряду і відносно велику масу.

    навчальні цілі

    • Охарактеризуйте експеримент із золотою фольгою Гейгера та Марсдена під керівництвом Резерфорда та його наслідки для моделі атома

    Модель Резерфорда - це модель атома, названого на честь Ернеста Резерфорда. Резерфорд керував знаменитим експериментом Гейгера-Марсдена в 1909 році, який припустив, згідно з аналізом Резерфорда 1911 року, що так звана «модель сливового пудингу» атома Джей Джей Томсона була неправильною. Нова модель Резерфорда для атома, заснована на експериментальних результатах, містила нові риси відносно високого центрального заряду, сконцентрованого в дуже малому обсязі в порівнянні з рештою атома. Цей центральний обсяг також містив основну частину маси атома. Пізніше цей регіон буде названий «ядром».

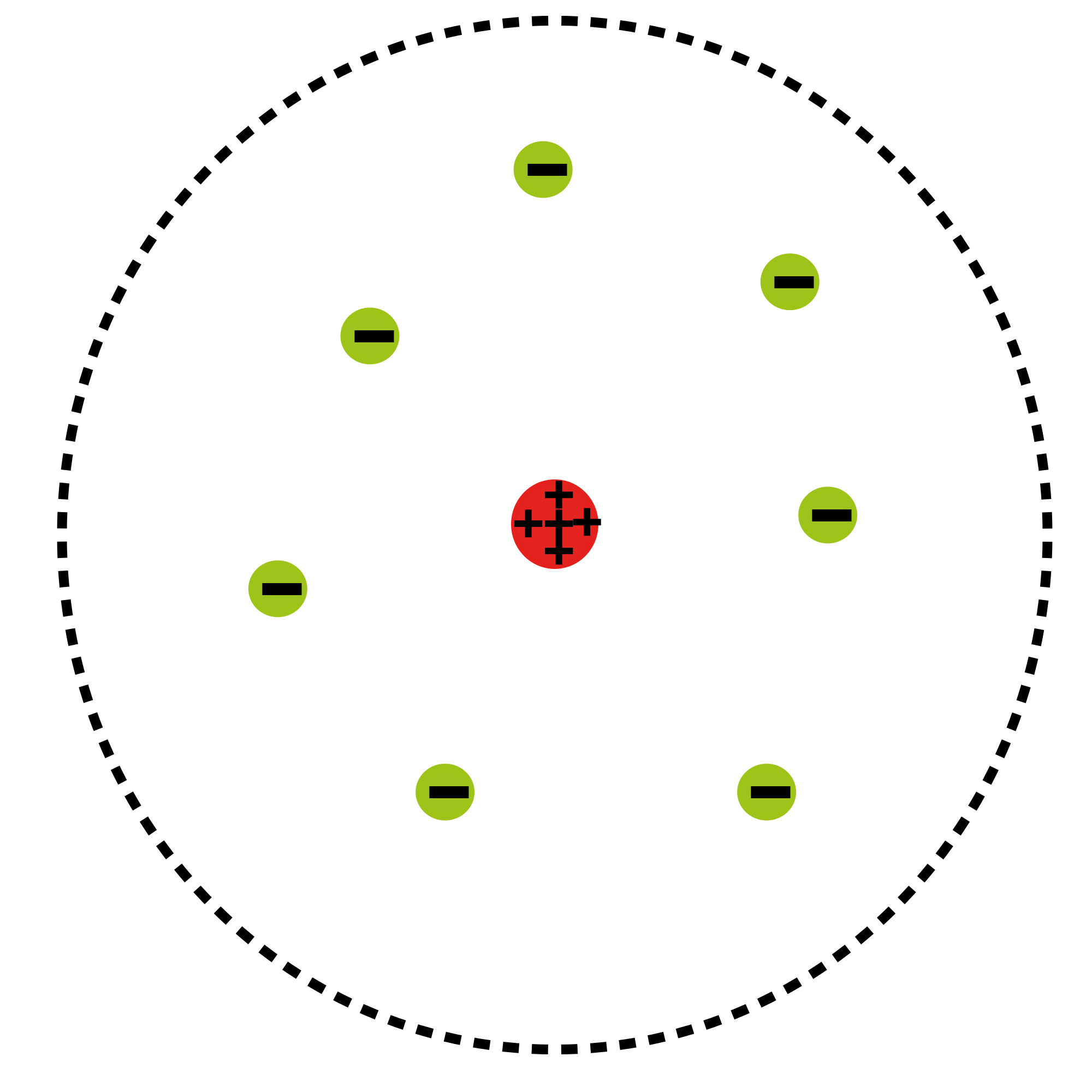
    зображення

    Атомна планетарна модель: Основна діаграма атомної планетарної моделі; електрони - зеленим кольором, а ядро - червоним

    У 1911 році Резерфорд розробив експеримент для подальшого вивчення атомної структури з використанням альфа-частинок, що випромінюються радіоактивним елементом. Слідуючи його напрямку, Гейгер і Марсден стріляли альфа-частинки з великими кінетичними енергіями в напрямку тонкої фольги золота. Очікувалося, що вимірювання картини розсіяних частинок дасть інформацію про розподіл заряду всередині атома. За переважною моделлю сливового пудингу всі альфа-частинки повинні бути відхилені, максимум, на кілька градусів. Однак фактичні результати здивували Резерфорда. Хоча багато альфа-частинок проходили, як очікувалося, багато інших відхилялися під невеликими кутами, тоді як інші відбивалися назад до альфа-джерела.

    З чисто енергетичних міркувань того, наскільки далеко частинки відомої швидкості зможуть проникнути до центрального заряду 100 е, Резерфорд зміг обчислити, що радіус його золотого центрального заряду повинен бути менше 3,4⋅10−143,4⋅10−14 метрів. Це було в атомі золота, який, як відомо, має радіус близько 10−1010−10 метрів; дуже дивовижна знахідка, оскільки передбачала сильний центральний заряд менше 1300013000 го діаметра атома.

    Вступ до історії атомної теорії - Резерфордська модель: Резерфорд, Томсон, електрони, ядра та сливи. Я не маю на увазі бути бором, але чи вважаєте ви, що пудинг повинен мати певну роль у серйозному науковому дослідженні?

    Модель Бора атома

    Бор припустив, що електрони у водні можуть мати певні класичні рухи лише тоді, коли вони обмежені квантовим правилом.

    навчальні цілі

    • Охарактеризуйте модель атома, запропоновану Нільсом Бором.

    Модель Бора атома

    Великий датський фізик Нільс Бор (1885—1962 рр.) негайно використав планетарну модель атома Резерфорда. Бор переконався в його дійсності і провів частину 1912 року в лабораторії Резерфорда. У 1913 році, повернувшись до Копенгагена, він почав публікувати свою теорію найпростішого атома, водню, засновану на планетарній моделі атома.

    зображення

    Нільс Бор: Нільс Бор, датський фізик, використав планетарну модель атома для пояснення атомного спектра та розміру атома водню. Його численні внески у розвиток атомної фізики та квантової механіки; його особистий вплив на багатьох студентів та колег; і його особиста цілісність, особливо перед обличчям нацистських утисків, принесли йому чільне місце в історії. (кредит: Невідомий автор, через Wikimedia Commons)

    Протягом десятиліть задавалося багато питань щодо атомних характеристик. Від їх розмірів до їх спектрів було відомо багато про атоми, але мало що було пояснено з точки зору законів фізики. Теорія Бора пояснила атомний спектр водню, зробила його миттєво відомим і встановила нові і широко застосовні принципи в квантовій механіці.

    Одна велика головоломка, яку мала планетарна модель атома, полягала в наступному. Закони класичної механіки передбачають, що електрон повинен випускати електромагнітне випромінювання при обертанні ядра (згідно з рівняннями Максвелла, прискорюючий заряд повинен випромінювати електромагнітне випромінювання). Оскільки електрон втрачав енергію, він поступово обертається всередину, руйнуючись в ядро. Ця модель атома є катастрофічною, оскільки пророкує, що всі атоми нестабільні. Крім того, коли електронні спіралі всередину, випромінювання поступово збільшуватиметься в частоті, оскільки орбіта стає все меншою та швидшою. Це призвело б до безперервного мазок, по частоті, електромагнітного випромінювання. Однак в кінці 19 століття експерименти з електричними розрядами показали, що атоми будуть випромінювати світло (тобто електромагнітне випромінювання) тільки на певних дискретних частотах.

    Щоб подолати цю складність, Нільс Бор запропонував у 1913 році те, що зараз називається моделлю Бора атома. Він припустив, що електрони можуть мати лише певні класичні рухи:

    1. Електрони в атомах обертаються навколо ядра.
    2. Електрони можуть тільки стабільно орбіти, не випромінюючи, на певних орбітах (названих Бором «стаціонарними орбітами»): на певному дискретному наборі відстаней від ядра. Ці орбіти пов'язані з певними енергіями і називаються також енергетичними оболонками або енергетичними рівнями. На цих орбітах прискорення електрона не призводить до втрат випромінювання та енергії, як того вимагає класична електродинаміка.
    3. Електрони можуть тільки набирати і втрачати енергію, перестрибуючи з однієї дозволеної орбіти на іншу, поглинаючи або випромінюючи електромагнітне випромінювання з частотою α, що визначається різницею енергій рівнів відповідно до відношення Планка:

    \[\Delta \mathrm { E } = \mathrm { E } _ { 2 } - \mathrm { E } _ { 1 } = \mathrm { h } \nu\]

    \(\mathrm{h}\)де постійна\(\nu\) Планка і частота випромінювання.

    напівкласична модель

    Значення моделі Бора полягає в тому, що закони класичної механіки застосовуються до руху електрона про ядро тільки при обмеженні квантовим правилом. Тому його атомна модель називається напівкласичної моделлю.

    Основні припущення моделі Бора

    Бор успішно пояснив спектр водню, прийнявши умову квантування та ввівши константу Планка у свою модель.

    навчальні цілі

    • Опишіть основні припущення, які були застосовані Нільсом Бором до планетарної моделі атома

    У попередніх модулів ми бачили головоломки з класичних атомних теорій (наприклад, модель Резерфорда). Найголовніше, що класична електродинаміка передбачає, що атом, описаний (класичною) планетарною моделлю, буде нестабільним. Щоб пояснити загадку, Бор запропонував те, що зараз називається Борською моделлю атома в 1913 році. Він припустив, що електрони можуть мати лише певні класичні рухи:

    1. Електрони в атомах обертаються навколо ядра.
    2. Електрони можуть тільки стабільно орбіти, не випромінюючи, на певних орбітах (названих Бором «стаціонарними орбітами») на певному дискретному наборі відстаней від ядра. Ці орбіти пов'язані з певними енергіями і називаються також енергетичними оболонками або енергетичними рівнями. На цих орбітах прискорення електрона не призводить до втрат випромінювання та енергії, як того вимагає класична електродинаміка.
    3. Електрони можуть тільки набирати і втрачати енергію, перестрибуючи з однієї дозволеної орбіти на іншу, поглинаючи або випромінюючи електромагнітне випромінювання з частотою α, що визначається різницею енергій рівнів відповідно до відношення Планка:\(\Delta \mathrm { E } = \mathrm { E } _ { 2 } - \mathrm { E } _ { 1 } = \mathrm { h } \nu\), де\(\mathrm{h}\) - постійна Планка. Крім того, Бор також припускав, що кутовий момент\(\mathrm{L}\) обмежений цілим числом кратним фіксованої одиниці:\(\mathrm { L } = \mathrm { n } \frac { \mathrm { h } } { 2 \pi } = \mathrm { n } \hbar \), де\(\mathrm { n } = 1,2,3 , \dots \) називається основним квантовим числом, і\(\hbar = \frac { h } { 2 \pi }\).

    Ми бачили, що Планк прийняв нову умову квантування енергії, щоб пояснити випромінювання чорного тіла, де він вперше ввів постійну Планка hh. Незабаром після цього Ейнштейн вдався до цієї нової концепції квантування енергії і знову використав постійну Планка для пояснення фотоелектричних ефектів, в яких він припустив, що електромагнітне випромінювання взаємодіє з речовиною як частинки (пізніше названі «фотонами»). Тут Бор вперше успішно пояснив атомний водневий спектр, прийнявши умову квантування та ввівши константу Планка у свою атомну модель. У період радикального розвитку на початку 20-го століття фізики почали розуміти, що для пояснення мікроскопічних світів важливо ввести поняття «квантування».

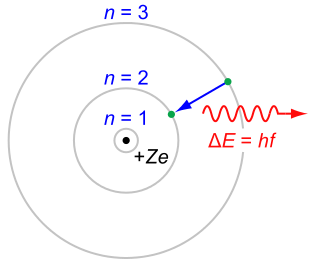
    зображення

    Модель Резерфорда-Бора: Резерфорда-Бора модель атома водню (\(\mathrm{Z=1}\)) або воднеподібного іона (\(\mathrm{Z>1}\)), де негативно заряджений електрон, обмежений атомною оболонкою, оточує невелике, позитивно заряджене атомне ядро, і де супроводжується стрибок електронів між орбітами за випромінюваної або поглиненої кількості електромагнітної енергії (hhν). Орбіти, по яких може подорожувати електрон, показані у вигляді сірих кіл; їх радіус збільшується як\(\mathrm{n^2}\), де\(\mathrm{n}\) головне квантове число. Зображений тут\(\mathrm{3→2}\) перехід дає першу лінію ряду Бальмера, а для водню (\(\mathrm{Z=1}\)) він призводить до фотона довжиною хвилі 656 нм (червоне світло).

    Орбіти Бора

    За Бора, електрони можуть тільки стабільно орбіти, на певних орбітах, на певному дискретному наборі відстаней від ядра.

    навчальні цілі

    • Поясніть взаємозв'язок між «орбітами Бора» та ефектом квантування

    Датський фізик Нілс Бор був досить розумний, щоб відкрити метод обчислення електронних орбітальних енергій у водні. Як ми бачили в попередньому модулі «Модель Атома Бора», Бор припускав, що електрони можуть обертатися стабільно, не випромінюючи, на певних орбітах (названих Бором як «стаціонарні орбіти»), на певному дискретному наборі відстаней від ядра. Ці «орбіти Бора» мають дуже важливу особливість квантування, як показано нижче. Це був важливий перший крок, який був вдосконалений, але варто повторити тут, оскільки він правильно описує багато характеристик водню. Припускаючи кругові орбіти, Бор запропонував квантувати кутовий момент LL електрона на його орбіті, тобто має тільки конкретні, дискретні значення. Значення для LL задається за формулою:

    \[\mathrm { L } = \mathrm { m } _ { \mathrm { e } } \mathrm { vr } _ { \mathrm { n } } = \mathrm { n } \dfrac { \mathrm { h } } { 2 \pi } = \mathrm { n } \hbar\]

    де LL - момент імпульсу, мем - маса електрона, rnrn - радіус n-ї орбіти, а hh - константа Планка. Зверніть увагу, що кутовий імпульс є\(\mathrm { L } = \mathrm { I } \omega\). Для невеликого об'єкта в радіусі\(\mathrm{r, I=mr^2}\) і\(\mathrm{ω=\frac{v}{r}}\), так що:

    \[\mathrm { L } = \left( \mathrm { mr } ^ { 2 } \right) \left( \dfrac { \mathrm { v } } { \mathrm { r } } \right) = \mathrm { mvr }\]

    Квантування говорить про те, що це значення mvrmvr може мати тільки дискретні значення. У той час сам Бор не знав, чому слід квантувати кутовий імпульс, але використовуючи це припущення, він зміг обчислити енергії у водневому спектрі, чого ніхто інший не робив у той час.

    Нижче наведена діаграма енергетичного рівня, яка є зручним способом відображення енергетичних станів - дозволених енергетичних рівнів електрона (щодо нашого обговорення). Енергія наноситься вертикально з найнижчим або заземленим станом внизу і з порушеними станами вище. З огляду на енергії ліній в атомному спектрі, можна (хоча іноді дуже складно) визначити енергетичні рівні атома. Діаграми енергетичного рівня використовуються для багатьох систем, включаючи молекули і ядра. Теорія атома або будь-яка інша система повинна передбачати його енергії на основі фізики системи.

    зображення

    Графік діаграми рівня енергії: Діаграма рівня енергії відображає енергію вертикально і корисна для візуалізації енергетичних станів системи та переходів між ними. Ця діаграма призначена для атомів водню, що показує перехід між двома орбітами, що мають енергії\(\mathrm{E_4}\) і\(\mathrm{E_2}\).

    Енергія орбіти Бора

    Виходячи зі своїх припущень, Бор вивів кілька важливих властивостей атома водню з класичної фізики.

    навчальні цілі

    • Застосовуйте правильне рівняння для обчислення рівнів енергії та енергії випромінюваного фотона для воднеподібного атома

    З припущень Бора ми тепер виведемо ряд важливих властивостей атома водню з класичної фізики. Почнемо з того, що відзначаємо доцентрову силу, яка змушує електрон слідувати круговому шляху, що подається кулонівською силою. Якщо бути більш загальним, відзначимо, що даний аналіз справедливий для будь-якого одноелектронного атома. Отже, якщо ядро має протони ZZ (Z = 1Z = 1 для водню, Z = 2Z = 2 для гелію тощо) і лише один електрон, цей атом називається воднеподібним атомом.

    Спектри воднеподібних іонів схожі на водню, але зміщені до вищої енергії більшою силою притягання між електроном і ядром. Величина доцентрової сили дорівнює m2evrnmev2rn, тоді як кулонівська сила Zkee2R2Zkee2R2. Мовчазне припущення тут полягає в тому, що ядро більш масивне, ніж стаціонарний електрон, і електрон обертається навколо нього. Це узгоджується з планетарною моделлю атома. Прирівнюючи ці:

    \[\dfrac { \mathrm { m } _ { \mathrm { e } } \mathrm { v } ^ { 2 } } { \mathrm { r } } = \dfrac { \mathrm { Z } \mathrm { k } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } { \mathrm { r } ^ { 2 } }\]

    Це рівняння визначає швидкість електрона при будь-якому радіусі:

    \[\mathrm{ v } = \dfrac { \sqrt { \mathrm{ Z k } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } } { \mathrm { m } _ { \mathrm { e } } \mathrm { r } }\]

    Він також визначає загальну енергію електрона на будь-якому радіусі:

    \[\mathrm { E } = \dfrac { 1 } { 2 } \mathrm { m } _ { \mathrm { e } } \mathrm { v } ^ { 2 } - \frac { \mathrm { Zk } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } { \mathrm { r } } = - \dfrac { \mathrm { Z } \mathrm { k } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } { 2 \mathrm { r } }\]

    Загальна енергія негативна і обернено пропорційна rr. Це означає, що потрібна енергія, щоб відтягнути орбітальний електрон від протона. Для нескінченних значень rr енергія дорівнює нулю, що відповідає нерухомому електрону, нескінченно далекому від протона.

    Тепер ось квантове правило: Як ми бачили в попередньому модулі, кутовий момент L = mervl = Merv є цілим числом кратним:

    \[\mathrm { m } _ { \mathrm { e } } \mathrm { vr } = \mathrm { n } \hbar\]

    Підставляючи вираз в рівняння на швидкість вище дає рівняння для rr через nn:

    \[\sqrt { \mathrm { Zk } _ { \mathrm { e } } \mathrm { e } ^ { 2 } \mathrm { m } _ { \mathrm { e } } \mathrm { r } } = \mathrm { n } \hbar\]

    Допустимий радіус орбіти при будь-якому n тоді дорівнює:

    \[\mathrm { r } _ { \mathrm { n } } = \dfrac { \mathrm { n } ^ { 2 } \hbar ^ { 2 } } { \mathrm { Zk } _ { \mathrm { e } } \mathrm { e } ^ { 2 } \mathrm { m } _ { \mathrm { e } } }\]

    Найменше можливе значення rr в атомі водню називається радіусом Бора і дорівнює 0,053 нм. Енергія n-го рівня для будь-якого атома визначається радіусом і квантовим числом:

    \[\mathrm { E } = - \dfrac { \mathrm { Zk } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } { 2 \mathrm { r } _ { \mathrm { n } } } = - \dfrac { \mathrm { Z } ^ { 2 } \left( \mathrm { k } _ { \mathrm { e } } \mathrm { e } ^ { 2 } \right) ^ { 2 } \mathrm { m } _ { \mathrm { e } } } { 2 \hbar ^ { 2 } \mathrm { n } ^ { 2 } } \approx \dfrac { - 13.6 \mathrm { Z } ^ { 2 } } { \mathrm { n } ^ { 2 } } \mathrm { eV }\]

    Використовуючи це рівняння, енергія фотона, що випромінюється атомом водню, задається різницею двох рівнів енергії водню:

    \[\mathrm { E } = \mathrm { E } _ { \mathrm { i } } - \mathrm { E } _ { \mathrm { f } } = \mathrm { R } \left( \dfrac { 1 } { \mathrm { n } _ { \mathrm { f } } ^ { 2 } } - \dfrac { 1 } { \mathrm { n } _ { \mathrm { i } } ^ { 2 } } \right)\]

    Яка формула Рідберга описує весь водневий спектр, а RR - постійна Рідберга. Модель Бора надзвичайно добре передбачила експериментальний водневий спектр.

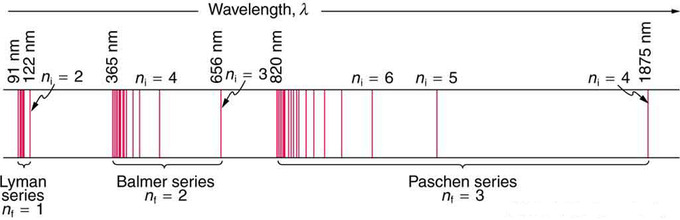
    зображення

    Рис. 1: На схемі водневого спектра показано кілька серій, названих для тих, хто найбільше сприяв їх визначенню. Частина серії Balmer знаходиться у видимому спектрі, тоді як серія Lyman повністю знаходиться в УФ, а серія Пашена та інші знаходяться в ІЧ. Значення nf та ni показані для деяких рядків.

    водневі спектри

    Спостережувані довжини хвиль водневого спектра можна обчислити за наступною формулою:\(\frac { 1 } { \lambda } = \mathrm { R } \left( \frac { 1 } { \mathrm { n } _ { \mathrm { f } } ^ { 2 } } - \frac { 1 } { \mathrm { n } _ { \mathrm { i } } ^ { 2 } } \right)\).

    навчальні цілі

    • Поясніть різницю між серіями Лаймана, Балмера та Пашена

    Протягом десятиліть задавалося багато питань щодо атомних характеристик. Від їх розмірів до їх спектрів було відомо багато про атоми, але мало що було пояснено з точки зору законів фізики. Атомні та молекулярні емісії та поглинання спектри були відомі протягом століття, щоб бути дискретними (або квантованими). Максвелл та інші зрозуміли, що між спектром атома і його структурою повинен бути зв'язок, щось на зразок резонансних частот музичних інструментів. Але, незважаючи на багаторічні зусилля багатьох великих умів, ні у кого не було працездатної теорії. (Це був жарт, що будь-яку теорію атомних і молекулярних спектрів можна знищити, кинувши на неї книгу даних, настільки складними були спектри.) Після пропозиції Ейнштейна про фотони з квантованими енергіями, прямо пропорційними їх довжинам хвиль, стало ще більш очевидним, що електрони в атомах можуть існувати тільки на дискретних орбітах.

    У деяких випадках вдалося розробити формули, які описували спектри випромінювання. Як і слід було очікувати, найпростіший атом - водень, з його єдиним електроном - має відносно простий спектр. Водневий спектр спостерігався в інфрачервоному (ІЧ), видимому та ультрафіолетовому (УФ), і спостерігалося кілька серій спектральних ліній. Спостережувані довжини хвиль водневого спектра можна обчислити за наступною формулою:

    \[\dfrac { 1 } { \lambda } = R \left( \dfrac { 1 } { n _ { f } ^ { 2 } } - \dfrac { 1 } { n _ { i } ^ { 2 } } \right)\]

    де\(\mathrm{λ}\) - довжина хвилі випромінюваного ЕМ-випромінювання і\(\mathrm{R}\) постійна Рідберга, визначена експериментом бути\(\mathrm{R=1.097⋅107 \; m^{−1}}\), і\(\mathrm{n_f, n_i}\) є додатними цілими числами, пов'язаними з певним рядом.

    Ці серії названі на честь ранніх дослідників, які вивчали їх особливо глибоко. Для серії Lyman,\(\mathrm { n } _ { \mathrm { f } } = 1\) для серії Balmer,\(\mathrm { n } _ { \mathrm { f } } = 2\); для серії Пашена,\(\mathrm { n } _ { \mathrm { f } } = 3\); і так далі. Серія Lyman повністю знаходиться в УФ, тоді як частина серії Balmer видно з рештою УФ. Серія Paschen та всі інші повністю IR. Мабуть, існує необмежена кількість серій, хоча вони поступово лежать далі в інфрачервоному діапазоні і їх важко спостерігати як nfnfincreases. Константа nini є натуральним числом, але воно повинно бути більше\(\mathrm{n_f}\). Таким чином, для серії Balmer,\(\mathrm{n_f=2}\) і\( \mathrm { n } _ { \mathrm { i } } = 3,4,5,6 \ldots \). Зверніть увагу, що ніні може наближатися до нескінченності.

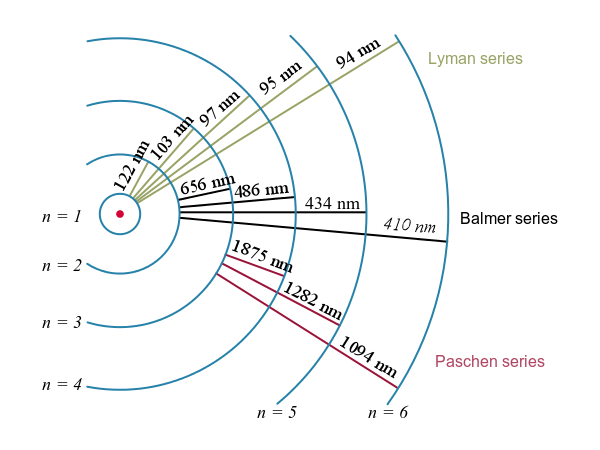
    зображення

    Електронні переходи та їх результуючі довжини хвиль для водню. : Рівні енергії не повинні масштабуватися.

    Хоча формула в рівнянні довжин хвиль була лише рецептом, призначеним для відповідності даних і не базувалася на фізичних принципах, вона мала на увазі більш глибокий сенс. Бальмер вперше розробив формулу лише для свого ряду, і пізніше було встановлено, що він описує всі інші серії, використовуючи різні значення nfnf. Бор першим осягнув глибший сенс. Знову ж таки, ми бачимо взаємодію експерименту та теорії у фізиці. Експериментальним шляхом спектри були добре встановлені, знайдено рівняння, яке відповідає експериментальним даними, але теоретичної основи не вистачало.

    де Бройлі та модель Бора

    Припускаючи, що електрон описується хвилею і має відповідати ціла кількість довжин хвиль, ми виведемо припущення квантування Бора.

    навчальні цілі

    • Охарактеризуйте переосмислення стану Бора де Броґлі

    Умова Бора, що кутовий момент є цілим числом кратним, пізніше було переосмислено в 1924 році де Брольє як умова стоячої хвилі. Хвилеподібні властивості речовини були згодом підтверджені спостереженнями електронної інтерференції при розсіюванні від кристалів. Електрони можуть існувати тільки в місцях, де вони конструктивно заважають. Як це впливає на електрони на атомних орбітах? Коли електрон пов'язаний з атомом, його довжина хвилі повинна вписуватися в невеликий простір, щось на зразок стоячої хвилі на струні.

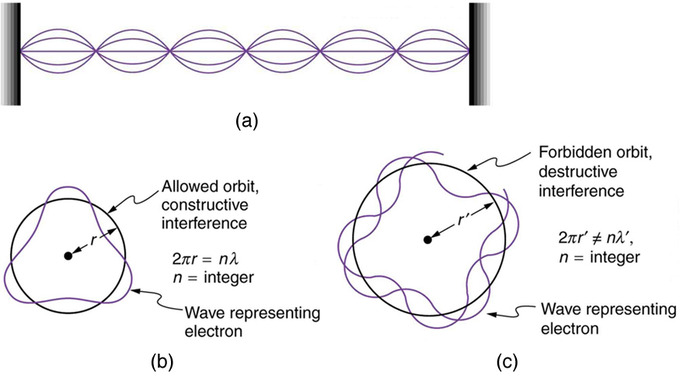
    зображення

    Хвилі на рядку: (a) Хвилі на рядку мають довжину хвилі, пов'язану з довжиною рядка, що дозволяє їм конструктивно втручатися. (б) Якщо уявити струну, зігнуту в замкнуте коло, ми отримаємо приблизне уявлення про те, як електрони на кругових орбітах можуть конструктивно перешкоджати. (c) Якщо довжина хвилі не вписується в окружність, електрон заважає руйнівно; він не може існувати на такій орбіті.

    Допустимі орбіти - це ті, в яких електрон конструктивно заважає собі. Не всі орбіти створюють конструктивні перешкоди, і тому допускаються лише певні орбіти (тобто орбіти квантуються). Припускаючи, що електрон описується хвилею і ціле число довжин хвиль повинно відповідати по окружності орбіти електрона, ми маємо рівняння:

    \[\mathrm { n } \lambda = 2 \pi \mathrm { r }\]

    Заміна довжини хвилі де Бройля hphp відтворює правило Бора. Оскільки λ=h/mevλ=h/mev, ми тепер маємо:

    \[\dfrac { \mathrm { nh } } { \mathrm { m } _ { \mathrm { ev } } } = 2 \pi \mathrm { r } _ { \mathrm { n } }\]

    Переставляючи терміни, і зауваживши, що l=mvrl=MVR для кругової орбіти, отримано квантування моменту моменту як умова дозволених орбіт:

    \[\mathrm { L } = \mathrm { m } _ { \mathrm { e } } \mathrm { vr } _ { \mathrm { n } } = \mathrm { n } \frac { \mathrm { h } } { 2 \pi } , ( \mathrm { n } = 1,2,3 \dots )\]

    Як було зазначено раніше, Бор був змушений висунути гіпотезу про це правило щодо дозволених орбіт. Зараз ми розуміємо це як умову конструктивної інтерференції електрона на круговій орбіті.

    Відповідно, новий вид механіки, квантова механіка, був запропонований в 1925 році. Модель Бора електронів, що рухаються по квантованим орбітах, була розширена на більш точну модель руху електронів. Нову теорію запропонував Вернер Гейзенберг. За різними міркуваннями інша форма тієї ж теорії, хвильова механіка, була відкрита самостійно австрійським фізиком Ервіном Шредінгером. Шредінгер використовував матеріальні хвилі де Броля, але натомість шукав хвильові рішення тривимірного хвильового рівняння. Це описувало електрони, які були обмежені рухатися навколо ядра воднеподібного атома, потрапляючи в пастку потенціалом позитивного ядерного заряду.

    де Броґлі матеріальні хвилі виправдовують магічні електронні орбітальні радіуси Бора: Я включаю короткий зміст електронної структури атома водню та пояснюю, як електрон може втручатися в себе на орбіті так само, як це може в експерименті з подвійною щілиною.

    Рентгенівські промені та ефект Комптона

    Комптон пояснив зсув частоти рентгенівського випромінювання/електронного розсіювання, приписуючи частинкоподібний імпульс до «фотонів».

    навчальні цілі

    • Опишіть ефекти Комптона між електронами та рентгенівськими фотонами

    До початку 20 століття дослідження взаємодії рентгенівських променів з речовиною були добре проведені. Було помічено, що коли рентгенівські промені відомої довжини хвилі взаємодіють з атомами, рентгенівські промені розсіюються через кут θ і виникають на іншій довжині хвилі, пов'язаної з θ. Хоча класичний електромагнетизм передбачив, що довжина хвилі розсіяних променів повинна дорівнювати початковій довжині хвилі, численні експерименти виявили, що довжина хвилі розсіяних променів довша (відповідає меншій енергії), ніж початкова довжина хвилі.

    У 1923 році Комптон опублікував статтю у Physical Review, яка пояснила рентгенівський зсув, приписуючи частинкоподібний імпульс «фотонам», на які Ейнштейн посилався у своєму поясненні фотоелектричного ефекту, що отримав Нобелівську премію. Вперше постульовані Планком, ці «частинки» концептуалізували «квантовані» елементи світла як містять певну кількість енергії залежно лише від частоти світла. У своїй роботі Комптон вивів математичну залежність між зсувом довжини хвилі і кутом розсіювання рентгенівських променів, припускаючи, що кожен розсіяний рентгенівський фотон взаємодіяв лише з одним електроном. Його стаття завершується повідомленням про експерименти, які перевіряли його похідне відношення:

    \[\lambda ^ { \prime } - \lambda = \dfrac { \mathrm { h } } { \mathrm { m } _ { \mathrm { e } } \mathrm { c } } ( 1 - \cos \theta ) \]

    де λ\ лямбда - початкова довжина хвилі, λ′\ lambda' - довжина хвилі після розсіювання,\(\mathrm{h}\) є постійною Планка,\(\mathrm{m_e}\) є Масою спокою Електрона,\(\mathrm{c}\) швидкість світла, а θ\ theta - кут розсіювання. Величина\(\mathrm{\frac{h}{m_e c} }\) відома як довжина хвилі Комптона електрона; вона дорівнює\(\mathrm{2.43⋅10^{−12}}\) m\(\mathrm{λ‘−λ}\) Зсув довжини хвилі щонайменше нуль (for\(\mathrm{θ=0°}\)) і максимум вдвічі перевищує довжину хвилі Комптона електрона (for\(\mathrm{θ=0°}\)). (Виведення формули Комптона трохи тривале і тут не буде розглянуто.)

    зображення

    Фотон стикається з ціллю в спокої: Фотон довжини хвилі λλ надходить зліва, стикається з ціллю в спокої, і новий фотон довжини хвилі λ'λ' виникає під кутом θ.

    Оскільки масова енергія та імпульс системи повинні бути збережені, як правило, електрон не може просто рухатися у напрямку падаючого фотона. Взаємодія між електронами та фотонами високої енергії (порівнянна з енергією решти електрона, 511 кеВ) призводить до того, що електрону дається частина енергії (робить його віддачею), а фотон, що містить енергію, що залишилася, випромінюється в іншому напрямку від оригіналу, так що загальний імпульс системи зберігається. Якщо у розсіяного фотона ще залишилося достатньо енергії, процес розсіювання Комптона може повторитися. У цьому сценарії електрон розглядається як вільний або нещільно пов'язаний. Фотони з енергією такого порядку знаходяться в рентгенівському діапазоні спектра електромагнітного випромінювання. Тому можна сказати, що ефекти Комптона (з електронами) відбуваються з рентгенівськими фотонами.

    Якщо фотон має нижчу енергію, але все ще має достатню енергію (загалом від декількох еВ до декількох кеВ, що відповідає видимому світлу через м'які рентгенівські промені), він може повністю викинути електрон зі свого атома-господаря (процес, відомий як фотоелектричний ефект), замість того, щоб зазнавати розсіювання Комптона. Фотони з вищою енергією (1.022 МеВ і вище, в діапазоні гамма-променів) можуть бомбардувати ядро і викликати утворення електрона та позитрона, процес, який називається парним виробництвом.

    Рентгенівські спектри: походження, дифракція кристалами та значення

    Рентген показує свою хвильову природу при випромінюванні на атомні/молекулярні структури і може бути використаний для їх вивчення.

    навчальні цілі

    • Опишіть взаємодії між рентгенівськими променями та атомами

    У попередньому атомі на рентгенівських променях ми бачили, що існує два процеси, за допомогою яких рентгенівські промені виробляються в аноді рентгенівської трубки. В одному процесі уповільнення електронів виробляє рентгенівські промені, і ці рентгенівські промені називаються Bremsstrahlung, або гальмівне випромінювання. Другий процес носить атомний характер і виробляє характерні рентгенівські промені, так звані тому, що вони характерні для анодного матеріалу. Рентгенівський спектр в характерний для того, що виробляється рентгенівською трубкою, показуючи широку криву випромінювання Bremsstrahlung з характерними рентгенівськими піками на ній.

    зображення

    Рентгенівський спектр: рентгенівський спектр, отриманий, коли енергійні електрони вражають матеріал, наприклад, в аноді ЕПТ. Гладка частина спектра - це гальмівне випромінювання, в той час як піки характерні для анодного матеріалу. Інший анодний матеріал мав би характерні рентгенівські піки на різних частотах.

    Оскільки рентгенівські фотони дуже енергійні, вони мають відносно короткі довжини хвиль. Наприклад, рентген 54,4-кеВ Kα, наприклад, має довжину хвилі\(\lambda = \frac { \mathrm { hc } } { \mathrm { E } } = 0.0228 \) нм. Таким чином, типові рентгенівські фотони діють як промені, коли стикаються з макроскопічними об'єктами, подібними до зубів, і виробляють різкі тіні. Однак оскільки атоми і атомні структури мають типовий розмір близько 0,1 нм, рентген показує з ними свою хвильову природу. Процес називається рентгенівською дифракцією, оскільки він включає дифракцію та інтерференцію рентгенівських променів для отримання візерунків, які можна проаналізувати для отримання інформації про структури, які розсіювали рентгенівські промені.

    Показаний нижче, Закон Брегга дає кути для когерентного і некогерентного розсіювання світла від кристалічної решітки, що відбувається при дифракції рентгенівського випромінювання. Коли рентген падає на атом, вони змушують електронну хмару рухатися як електромагнітна хвиля. Рух цих зарядів повторно випромінюють хвилі з однаковою частотою. Це називається Rayleigh Scrattering, яке ви повинні пам'ятати з попереднього атома. Подібне відбувається, коли нейтронні хвилі від ядер розсіюються від взаємодії з непарним електроном. Ці повторно випромінювані хвильові поля перешкоджають один одному або конструктивно, або деструктивно, і створюють дифракційну картину, яка захоплюється датчиком або плівкою. Це називається дифракцією Бреггса, і є основою для рентгенівської дифракції.

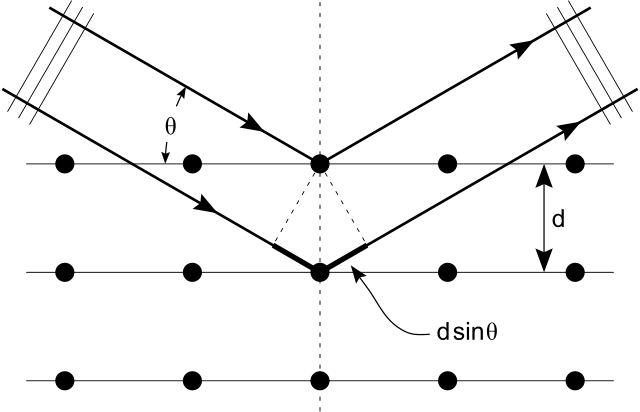
    зображення

    Рентгенівська дифракція: Закон Брегга про дифракцію: ілюстрація того, як рентгенівські промені взаємодіють з кристалічною решіткою.

    Мабуть, найвідомішим прикладом рентгенівської дифракції є відкриття подвійної спіралі структури ДНК в 1953 році. Використовуючи дані рентгенівської дифракції, дослідники змогли розрізнити структуру ДНК показує дифракційну картину, вироблену розсіюванням рентгенівських променів з кристала білка. Цей процес відомий як рентгенівська кристалографія через інформацію, яку він може дати про кристалічну структуру. Рентгенівські промені не тільки підтверджують розмір і форму атомів, вони також дають інформацію про атомні розташування в матеріалах. Наприклад, сучасні дослідження високотемпературних надпровідників включають складні матеріали, розташування решіток яких мають вирішальне значення для отримання надпровідного матеріалу. Їх можна вивчити за допомогою рентгенівської кристалографії.

    зображення

    Рентгенівська дифракція: рентгенівська дифракція від кристала білка, лізоциму курячого яйцеклітини, виробляла цю інтерференційну картину. Аналіз закономірності дає інформацію про будову білка.

    Ефект Комптона

    Ефект Комптона - явище зменшення енергії фотона при розсіюванні вільною зарядженою частинкою.

    навчальні цілі

    • Поясніть, чому Комптонське розсіювання - це непружне розсіювання.

    Комптонне розсіювання - це непружне розсіювання фотона вільною зарядженою частинкою (зазвичай електроном). Це призводить до зменшення енергії (збільшення довжини хвилі) фотона (який може бути рентгенівським або гамма-фотоном), званого ефектом Комптона. Частина енергії фотона передається розсіює електрону. Зворотне розсіювання Комптона також існує, і відбувається, коли заряджена частинка передає частину своєї енергії фотону.

    зображення

    Розсіювання в ефекті Комптона: Ефект Комптона - це назва розсіювання фотона електроном. Енергія і імпульс зберігаються, що призводить до зменшення обох для розсіяного фотона. Вивчаючи цей ефект, Комптон перевірив, що фотони мають імпульс.

    Комптонське розсіювання є прикладом непружного розсіювання, оскільки довжина хвилі розсіяного світла відрізняється від падаючого випромінювання. Все-таки походження ефекту можна розглядати як пружне зіткнення між фотоном і електроном. Величина зміни довжини хвилі називається зсувом Комптона. Хоча ядерне розсіювання Комптона існує, розсіювання Комптона зазвичай відноситься до взаємодії, що включає лише електрони атома.

    Ефект Комптона важливий, оскільки демонструє, що світло не можна пояснити чисто як хвильове явище. Розсіювання Томсона, класична теорія електромагнітної хвилі, розсіяної зарядженими частинками, не може пояснити зсуви низької інтенсивності довжини хвилі: класично світло достатньої інтенсивності для прискорення електричного поля зарядженої частинки до релятивістської швидкості спричинить віддачу радіаційного тиску і асоційований доплерівський зсув розсіяного світла. Однак ефект стане довільно малим при досить низькій інтенсивності світла незалежно від довжини хвилі. Світло повинно вести себе так, ніби воно складається з частинок, щоб пояснити низькоінтенсивне розсіювання Комптона. Експеримент Комптона переконав фізиків, що світло може вести себе як потік частиноподібних об'єктів (квантів), енергія яких пропорційна частоті.

    Ключові моменти

    • Британський фізик Джей Джей Томсон провів експерименти з вивченням катодних променів і виявив, що це унікальні частинки, пізніше названі електронами.
    • Резерфорд довів, що водневе ядро присутнє в інших ядрах.
    • У 1932 році Джеймс Чедвік показав, що в випромінюванні, яке він використовував, є незаряджені частинки. Ці частинки, пізніше названі нейтронами, мали подібну масу протонів, але не мали тих же характеристик, що і протони.
    • Атом - це основна одиниця речовини, яка складається з щільного центрального ядра, оточеного хмарою негативно заряджених електронів.
    • Розсіяні знання, виявлені алхіміками за середні століття, сприяли відкриттю атомів.
    • Дальтон встановив свою атомну теорію виходячи з того, що маси реагентів в конкретних хімічних реакціях завжди мають певне масове співвідношення.
    • Дж. Томсон, який відкрив електрон в 1897 році, запропонував модель атома сливового пудингу в 1904 році до відкриття атомного ядра, щоб включити електрон в атомну модель.
    • У моделі Томсона атом складається з електронів, оточених супом позитивного заряду, щоб збалансувати негативні заряди електронів, як негативно заряджені «сливи», оточені позитивно зарядженим «пудингом».
    • Модель Томсона 1904 року була спростована експериментом з золотої фольги Ганса Гейгера та Ернеста Марсдена 1909 року.
    • Резерфорд скасував модель Томсона в 1911 році своїм відомим експериментом із золотої фольги, в якому він продемонстрував, що атом має крихітне ядро з високою масою.
    • У своєму експерименті Резерфорд зауважив, що багато альфа-частинок відхилялися під невеликими кутами, тоді як інші відображалися назад до альфа-джерела.
    • Цю висококонцентровану, позитивно заряджену область називають «ядром» атома.
    • Згідно Бору: 1) Електрони в атомах орбітають ядро, 2) Електрони можуть тільки стабільно орбіти, не випромінюючи, на певних орбітах, і 3) Електрони можуть тільки набирати і втрачати енергію, перестрибуючи з однієї дозволеної орбіти на іншу.
    • Значення моделі Бора полягає в тому, що закони класичної механіки застосовуються до руху електрона про ядро тільки при обмеженні квантовим правилом. Тому його атомна модель називається напівкласичної моделлю.
    • Закони класичної механіки передбачають, що електрон повинен випускати електромагнітне випромінювання, обертаючись навколо ядра, припускаючи, що всі атоми повинні бути нестабільними!
    • Класична електродинаміка передбачає, що атом, описаний (класичною) планетарною моделлю, буде нестабільним.
    • Щоб пояснити водневий спектр, Бору довелося зробити кілька припущень, що електрони можуть мати лише певні класичні рухи.
    • Після насіннєвої роботи Планка, Ейнштейна та Бора фізики почали розуміти, що важливо ввести поняття «квантування» для пояснення мікроскопічних світів.
    • «Орбіти Бора» мають дуже важливу особливість квантування: що кутовий момент L електрона на його орбіті квантований, тобто має тільки специфічні, дискретні значення. Це призводить до рівняння\(\mathrm { L } = \mathrm { m } _ { \mathrm { e } } \mathrm { vr } _ { \mathrm { n } } = \mathrm { n } \frac { \mathrm { h } } { 2 \pi } = \mathrm { n } \hbar \).
    • На момент пропозиції сам Бор не знав, навіщо кутовий момент слід квантувати, але використовуючи це припущення, він зміг обчислити енергії в водневому спектрі.
    • Теорія атома або будь-якої іншої системи повинна передбачати його енергії на основі фізики системи, яку змогла зробити модель Бора.
    • За словами Бора, допустимий радіус орбіти при будь-якому\(\mathrm{n}\) є\(\mathrm { r } _ { \mathrm { n } } = \frac { \mathrm { n } ^ { 2 } h ^ { 2 } } { Z \mathrm{ k } _ { e } \mathrm { e } ^ { 2 } \mathrm { m } _ { e } }\). Найменше можливе значення rr в атомі водню називається радіусом Бора і дорівнює 0,053 нм.
    • Енергія n-го рівня у будь-якого атома є\(\mathrm { E } = \approx \frac { - 13.6 \mathrm { Z } ^ { 2 } } { \mathrm { n } ^ { 2 } } \mathrm { eV }\).
    • Енергія фотона, що випромінюється атомом водню, задається різницею двох рівнів енергії водню:\(\mathrm { E } = \mathrm { E } _ { \mathrm { i } } - \mathrm { E } _ { \mathrm { f } } = \mathrm { R } \left( \frac { 1 } { \mathrm { n } _ { \mathrm { f } } ^ { 2 } } - \frac { 1 } { \mathrm { n } _ { \mathrm { i } } ^ { 2 } } \right) \), яка відома як формула Рідберга.
    • Атомні та молекулярні емісії та поглинання спектри були відомі протягом століття, щоб бути дискретними (або квантованими).
    • Серії Lyman, Balmer і Paschen названі на честь ранніх дослідників, які вивчали їх особливо глибоко.
    • Бор був першим, хто дав теоретичне пояснення водневих спектрів.
    • Умова Бора, що кутовий момент є цілим числом кратним, пізніше було переосмислено в 1924 році де Брольє як умова стоячої хвилі.
    • Для того, що Бор був змушений висунути гіпотезу як правило для дозволених орбіт, концепція хвиль матерії де Броля пояснює це як умова конструктивної інтерференції електрона на круговій орбіті.
    • Модель Бора була застосована лише до воднеподібних атомів. У 1925 році з'явилися більш загальні форми опису (тепер їх називають квантовою механікою), завдяки Гейзенбергу і Шредінгеру.
    • Комптон вивів математичну залежність між зсувом довжини хвилі і кутом розсіювання рентгенівських променів.
    • Ефекти Комптона (з електронами) зазвичай виникають з рентгенівськими фотонами.
    • Якщо фотон більш низької енергії, у видимому світлі через м'який рентгенівський діапазон спостерігаються фотоелектричні ефекти. Фотони з вищою енергією, в діапазоні гамма-променів, можуть призвести до парного виробництва.
    • Рентгенівські промені є відносно високочастотним ЕМ-випромінюванням. Вони виробляються переходами між внутрішньооболонковими електронними рівнями, які виробляють рентгенівські промені, характерні для атомного елемента, або шляхом прискорення електронів.
    • Рентгенівська дифракція — це методика, яка дає детальну інформацію про кристалографічну структуру природних і виготовлених матеріалів.
    • Сучасні дослідження в матеріалознавстві та фізиці включають складні матеріали, розташування решітки яких мають вирішальне значення для отримання надпровідного матеріалу, який можна вивчити за допомогою рентгенівської кристалографії.

    Ключові умови

    • сцинтиляція: спалах світла, що утворюється в прозорому матеріалі при проходженні частинки.
    • альфа-частинка: позитивно заряджене ядро атома гелію-4 (що складається з двох протонів і двох нейтронів), що випромінюється як наслідок радіоактивності.
    • катод: електрод, через який електричний струм витікає з поляризованого електричного пристрою.
    • електромагнітна сила: велика фундаментальна сила, яка діє між зарядженими тілами, опосередкована обміном фотонами
    • Число Авогадро: кількість складових частинок (зазвичай атомів або молекул) в одному молі даної речовини. Він має розміри зворотної молі і його величина дорівнює\(6.02214129 \cdot 10^{23} \text{ mol}^{-1}\)
    • ядро: масивна, позитивно заряджена центральна частина атома, що складається з протонів і нейтронів
    • Рівняння Максвелла: Набір рівнянь, що описують, як електричні та магнітні поля генеруються та змінюються один одним і зарядами та струмами.
    • напівкласична: теорія, в якій одна частина системи описується квантово-механічно, тоді як інша трактується класично.
    • чорне тіло: ідеалізоване фізичне тіло, яке поглинає все падаюче електромагнітне випромінювання, незалежно від частоти або кута падіння. Хоча чорне тіло є теоретичним поняттям, ви можете знайти приблизні реалізації чорного тіла в природі.
    • фотоелектричний ефект: Виникнення електронів, що випромінюються з речовини (металів і неметалевих твердих тіл, рідин або газів) як наслідок їх поглинання енергії від електромагнітного випромінювання.
    • квантування: Процес пояснення класичного розуміння фізичних явищ з точки зору нового розуміння, відомого як квантова механіка.
    • доцентровий: спрямований або рухається до центру.
    • фотон: Квант світла та іншої електромагнітної енергії, що розглядається як дискретна частинка, що має нульову масу спокою, відсутність електричного заряду та невизначений тривалий термін служби.
    • спектр: умова, яка не обмежується певним набором значень, але може нескінченно змінюватися в межах континууму. Слово побачило своє перше наукове використання в області оптики для опису веселки кольорів у видимому світлі при розділенні за допомогою призми.
    • стояча хвиля: форма хвилі, яка виникає в обмеженому, фіксованому середовищі таким чином, що відбита хвиля збігається з отриманою хвилею. Поширеним прикладом є вібрація струн на музичному струнному інструменті.
    • хвиля матерії: Концепція відображає подвійність хвиля-частинки речовини. Теорія була запропонована Луї де Брольє.
    • гамма-промінь: дуже висока частота (і, отже, дуже висока енергія) електромагнітне випромінювання, що випромінюється як наслідок радіоактивності.
    • фотоелектричні ефекти: При фотоелектричних ефектах електрони випромінюються з речовини (металів і неметалевих твердих тіл, рідин або газів) як наслідок їх поглинання енергії від електромагнітного випромінювання.

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ