Skip to main content
LibreTexts - Ukrayinska

24.3: Лінзи

  1. Last updated
  2. Save as PDF
  • Page ID
    74630

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    навчальні цілі

    • Опишіть властивості тонкої лінзи і призначення трасування променів

    Тонкі лінзи та трасування променів

    Трасування променів - це техніка визначення або проходження (трасування) шляхів, які беруть світлові промені. Експерименти, а також наш власний досвід показують, що коли світло взаємодіє з предметами в кілька разів більшими за його довжину хвилі, воно подорожує прямими лініями і діє як промінь. (Промінь - це просто пряма лінія, яка бере початок в точці.) Його хвильові характеристики не виражені в таких ситуаціях. Оскільки довжина хвилі світла менше мікрона (тисячна частка міліметра), він діє як промінь у багатьох поширених ситуаціях, коли він стикається з предметами розміром більше мікрона, такими як лінзи.

    Для променів, що проходять через речовину, для простежування шляхів використовується закон заломлення. Тут ми використовуємо трасування променів, щоб допомогти нам зрозуміти дію лінз у ситуаціях, починаючи від формування зображень на плівці до збільшення дрібного друку до виправлення короткозорості. Хоча трасування променів для складних об'єктивів, таких як ті, що зустрічаються у складних камерах, може вимагати комп'ютерних методів, існує набір простих правил для відстеження променів через тонкі лінзи. Тонка лінза визначається як така, товщина якої дозволяє променям заломлюватися, як показано на малюнку, але не дозволяє таким властивостям, як дисперсія та аберації. Ідеальна тонка лінза має дві заломлюючі поверхні, але лінза досить тонка, щоб припустити, що світлові промені згинаються лише один раз. Інший спосіб сказати про це полягає в тому, що товщина лінзи набагато менше фокусної відстані лінзи. Тонка симетрична лінза має дві фокусні точки, по одній з обох сторін і обидві на однаковій відстані від лінзи. Ще одна важлива характеристика тонкої лінзи полягає в тому, що світлові промені через її центр відхиляються незначною кількістю, як видно в центральних променях на перших двох малюнках. Лікування лінзи як тонкої лінзи відоме як «наближення тонкої лінзи».

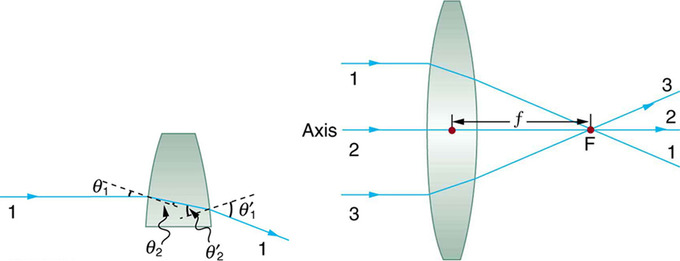
    зображення

    Опукла лінза: Промені світла, що надходять в об'єктив, що сходиться паралельно її осі, сходяться в її фокусній точці F (промінь 2 лежить на осі лінзи.) Відстань від центру лінзи до фокусної точки є фокусною відстанню об'єктива f Розширений огляд шляху, зробленого променем 1, показує перпендикуляри і кути падіння і заломлення на обох поверхнях.

    зображення

    Тонкі лінзи: Тонкі лінзи мають однакову фокусну відстань з обох сторін. (а) Паралельні світлові промені, що надходять в сходжувальну лінзу з правого хреста в її фокусній точці зліва. (b) Паралельні світлові промені, що надходять в розбіжну лінзу праворуч, здається, надходять від фокусної точки праворуч.

    Правила трасування променів

    За допомогою паперу, олівця та прямого краю трасування променів може точно описати роботу лінзи. Правила трасування променів для тонких лінз засновані на ілюстраціях, включених в цей розділ:

    1. Промінь, що входить в сходяться лінзу паралельно її осі, проходить через фокусну точку F лінзи з іншого боку. (Див. Промені 1 і 3 в.)
    2. Промінь, що входить в розбіжну лінзу паралельно її осі, здається, виходить з фокусної точки F (Див. Промені 1 і 3 в.)
    3. Промінь, що проходить через центр або сходяться, або розходяться лінзи, не змінює напрямок. (Див. Промінь 2 в і.)
    4. Промінь, що входить в сходяться лінзу через її фокусну точку, виходить паралельно її осі. (Реверс променів 1 і 3 в.)
    5. Промінь, який потрапляє в розбіжну лінзу, прямуючи до фокусної точки на протилежній стороні, виходить паралельно осі. (Реверс променів 1 і 3 в).

    зображення

    Розбіжна лінза: Промені світла, що надходять в розбіжну лінзу паралельно її осі, розходяться, і всі, здається, беруть початок в її фокусній точці F. Пунктирні лінії не є променями - вони вказують напрямки, з яких промені здаються надходять. Фокусна відстань f розходяться лінзи негативне. Розширений вид шляху, взятого променем 1, показує перпендикуляри і кути падіння і заломлення на обох поверхнях.

    Променеві діаграми, увігнута лінза та опукле дзеркало: показує, як малювати діаграми променів для розміщення зображення, отриманого увігнутою лінзою та опуклим дзеркалом.

    Рівняння тонкої лінзи та збільшення

    Рівняння тонкої лінзи пов'язує відстань об'єкта d o, відстань зображення d i та фокусну відстань f.

    навчальні цілі

    • Сформулюйте п'ять основних правил трасування променів

    Рівняння тонкої лінзи та збільшення

    Формування зображення тонкими лінзами

    Як лінза формує зображення предмета? Ми можемо використовувати техніку трасування променів, щоб проілюструвати, як лінзи утворюють зображення. Ми також можемо розробити рівняння для кількісного опису зображень. Нагадаємо п'ять основних правил трасування променів:

    1. Промінь, що входить в сходяться лінзу паралельно її осі, проходить через фокусну точку F лінзи з іншого боку.
    2. Промінь, що входить в розбіжну лінзу паралельно її осі, здається, виходить з фокусної точки F.
    3. Промінь, що проходить через центр або сходяться, або розходяться лінзи, не змінює напрямок.
    4. Промінь, що входить в сходяться лінзу через її фокусну точку, виходить паралельно її осі.
    5. Промінь, який потрапляє в розбіжну лінзу, прямуючи до фокусної точки на протилежній стороні, виходить паралельно осі.

    Розглянемо об'єкт на деякій відстані від сходяться лінзи, як показано в. Щоб знайти місце розташування і розмір сформованого зображення, простежуємо шляхи виділених світлових променів, що виходять з однієї точки на об'єкті (в даному випадку верхівки голови людини). На малюнку показано три промені з верхньої частини об'єкта, які можна простежити за допомогою п'яти правил трасування променів. Промені залишають цю точку, йдучи в багатьох напрямках, але ми концентруємося лише на декількох з шляхами, які легко простежити. Перший промінь - це той, який входить в лінзу паралельно її осі і проходить через фокусну точку з іншого боку (правило 1). Другий промінь проходить через центр лінзи без зміни напрямку (правило 3). Третій промінь проходить через найближчу фокусну точку на своєму шляху в лінзу і залишає лінзу паралельно її осі (правило 4). Три промені перетинаються в одній точці на іншій стороні лінзи. Зображення верхівки голови людини розташовується в цій точці. Всі промені, які йдуть з однієї точки на маківці голови людини, заломлюються таким чином, щоб перетинатися в зображеній точці. Промені з іншої точки на об'єкті, наприклад, її пряжка ременя, також перетинаються в іншій загальній точці, утворюючи повне зображення, як показано на малюнку. Хоча три промені простежуються, для розташування зображення необхідні лише два. Найкраще простежити промені, для яких існують прості правила трасування променів. Перш ніж застосовувати трасування променів до інших ситуацій, розглянемо приклад, показаний докладніше.

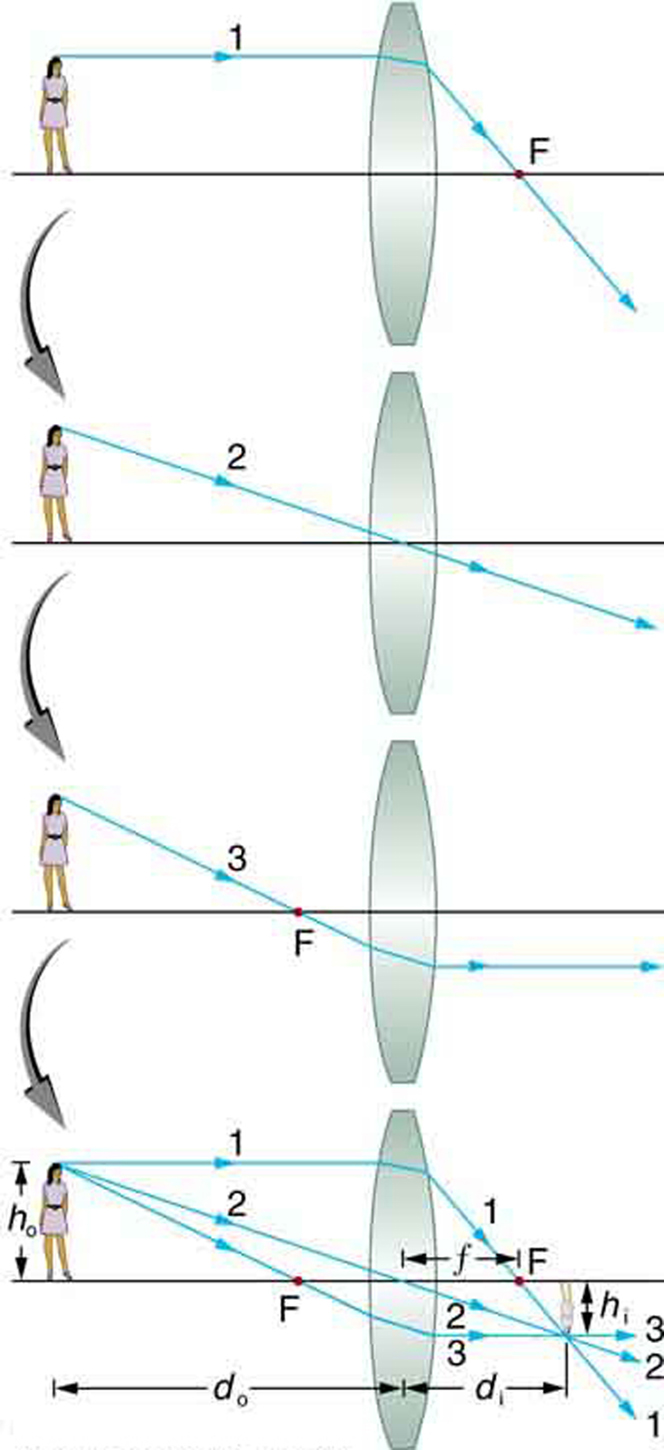
    зображення

    Формування зображення за допомогою тонкої лінзи: трасування променів використовується для визначення місцезнаходження зображення, утвореного лінзою. Промені, що походять з однієї точки на об'єкті, простежуються - три вибрані промені кожен дотримуються одного з правил трасування променів, так що їх шляхи легко визначити. Зображення розташовується в точці, де перетинаються промені. У цьому випадку формується реальне зображення - таке, яке можна спроектувати на екран.

    Кілька важливих відстаней з'являються в. Ми визначаємо d o як відстань об'єкта — відстань об'єкта від центру лінзи. Відстань зображення d i визначається як відстань зображення від центру об'єктива. Висота предмета і висота зображення задаються позначеннями h o і h i відповідно. Зображення, що відображаються вертикально відносно об'єкта, мають позитивні висоти, а ті, що перевернуті, мають негативну висоту. Використовуючи правила трасування променів і роблячи масштабний малюнок папером і олівцем, як у, ми можемо точно описати розташування і розмір зображення. Але реальна користь трасування променів полягає в візуалізації того, як зображення формуються в самих різних ситуаціях. Для отримання числової інформації ми використовуємо пару рівнянь, які можуть бути отримані з геометричного аналізу трасування променів для тонких лінз. Рівняння тонкої лінзи таке:

    \[\dfrac { 1 } { \mathrm { d } _ { o } } + \dfrac { 1 } { \mathrm { d } _ { \mathrm { i } } } = \dfrac { 1 } { \mathrm { f } }\]

    Ставлення висоти зображення до висоти об'єкта (h i/h o) визначаємо як збільшення m. Збільшення пов'язане з d o, d i, h o, а h i наступним співвідношенням:

    \[\dfrac { \mathrm { h } _ { \mathrm { i } } } { \mathrm { h } _ { \mathrm { o } } } = - \dfrac { \mathrm { d } _ { \mathrm { i } } } { \mathrm { d } _ { \mathrm { o } } } = \mathrm { m }\]

    У багатьох випадках обидва ці рівняння називаються разом рівнянням тонкої лінзи s. Рівняння тонких лінз широко застосовуються до всіх ситуацій, пов'язаних з тонкими лінзами (і «тонкими» дзеркалами).

    Рівняння тонких лінз для опуклої лінзи: показує, як використовувати рівняння тонкої лінзи для обчислення відстані зображення, висоти зображення та орієнтації зображення для опуклих лінз, коли відстань об'єкта більше фокусної відстані (f).

    комбінації лінз

    З'єднана лінза являє собою масив простих лінз із загальною віссю.

    навчальні цілі

    • Обчисліть фокусну відстань для складної лінзи з фокусних відстаней простих лінз

    СКЛАДОВІ ЛІНЗИ

    На відміну від простої лінзи, яка складається тільки з одного оптичного елемента, складна лінза являє собою масив простих лінз (елементів) із загальною віссю. Використання декількох елементів дозволяє корекцію більшої кількості оптичних аберацій, таких як хроматична аберація, викликана залежним від довжини хвилі індексом заломлення у склі, ніж це можливо за допомогою однієї лінзи. У багатьох випадках ці аберації можуть бути компенсовані значною мірою, використовуючи комбінацію простих лінз з додатковими абераціями.

    Найпростіший випадок, коли лінзи розміщуються в контакті: якщо лінзи фокусних відстаней f 1 і f 2 «тонкі», то комбінована фокусна відстань f лінз задається

    \[\dfrac { 1 } { f } = \dfrac { 1 } { f _ { 1 } } + \dfrac { 1 } { f _ { 2 } }\]

    Оскільки 1/ f - це сила лінзи, то видно, що сили тонких лінз в контакті є адитивними.

    Якщо дві тонкі лінзи розділені в повітрі деякою відстанню d (де d менше фокусної відстані першої лінзи), фокусна відстань для комбінованої системи задається

    \[\dfrac { 1 } { f } = \dfrac { 1 } { f _ { 1 } } + \dfrac { 1 } { f _ { 2 } } - \dfrac { d } { f _ { 1 } f _ { 2 } }\]

    ЗВОРОТНА ФОКУСНА ВІДСТАНЬ

    Відстань від другої лінзи до фокусної точки комбінованих лінз називається заднім фокусною відстанню (BFL).

    \[\mathrm { BFL } = \dfrac { \mathrm { f } _ { 2 } \left( \mathrm { d } - \mathrm { f } _ { 1 } \right) } { \mathrm { d } - \left( \mathrm { f } _ { 1 } + \mathrm { f } _ { 2 } \right) }\]

    Оскільки d прагне до нуля, значення BFL прагне до значення f, заданого для тонких лінз в контакті.

    Якщо відстань поділу дорівнює сумі фокусних відстаней (d = f 1 + f 2), то комбінована фокусна відстань і БФЛ нескінченні. Це відповідає парі лінз, які перетворюють паралельний (колімірованний) промінь в інший колімований промінь (див.). Цей тип системи називають афокальної системою, так як вона не виробляє сітчастої конвергенції або розбіжності променя. Дві лінзи при такому поділі утворюють найпростіший тип оптичного телескопа. Хоча система не змінює розбіжність колімованого променя, вона змінює ширину променя. Збільшення такого телескопа задається

    зображення

    Кеплерівський телескоп: Усі рефракційні телескопи використовують однакові принципи. Поєднання об'єктивної лінзи 1 та деякого типу окуляра 2 використовується для збору більше світла, ніж людське око могло зібрати самостійно, сфокусувати його 5 та представити глядачеві яскравіше, чіткіше та збільшене віртуальне зображення 6. Збільшення можна знайти, розділивши фокусну відстань об'єктива на фокусну відстань окуляра.

    \[\mathrm { M } = - \dfrac { \mathrm { f } _ { 2 } } { \mathrm { f } _ { 1 } }\]

    що є відношенням ширини вхідного пучка до ширини вихідного променя. Зверніть увагу на умовність знака: телескоп з двома опуклими лінзами (f 1 > 0, f 2 > 0) виробляє негативне збільшення, вказуючи на перевернуте зображення. Опукла плюс увігнута лінза (f 1 > 0 > f 2) створює позитивне збільшення, а зображення знаходиться вертикально.

    АХРОМАТИ

    Ахроматична лінза або ахромат - це лінза, яка призначена для обмеження ефектів хроматичної і сферичної аберації. Ахроматичні лінзи коригуються, щоб привести дві довжини хвиль (зазвичай червоний і синій/фіолетовий) у фокусі в одній площині.

    Найбільш поширеним типом ахромату є ахроматичний дублет, який складається з двох окремих лінз, виготовлених з окулярів з різною кількістю дисперсії. Зазвичай один елемент являє собою негативний (увігнутий) елемент, виготовлений з кресала, який має відносно високу дисперсію, а інший - позитивний (опуклий) елемент виготовлений з коронкового скла, яке має меншу дисперсію. Елементи лінз встановлені поруч один з одним, часто цементуються разом і формуються так, що хроматична аберація одного врівноважується іншою.

    У найбільш поширеному типі (показано на) позитивна потужність елемента лінзи коронки не зовсім зрівнюється негативною силою елемента лінзи кременя. Разом вони утворюють слабку позитивну лінзу, яка приведе дві різні довжини хвиль світла до загального фокусу. Також робляться негативні дублети, в яких переважає негативно-силовий елемент.

    зображення

    Ахроматичний дублет: (а) Хроматична аберація викликана залежністю індексу заломлення лінзи від кольору (довжини хвилі). Об'єктив більш потужний для фіолетового (V), ніж для червоного (R), створюючи зображення з різним розташуванням і збільшенням. (b) Багатолінзові системи, такі як цей ахроматичний дуплет, можуть частково виправляти хроматичні аберації, але вони можуть вимагати об'єктивів з різних матеріалів і додати до витрат оптичних систем, таких як камери.

    Рівняння лінзмейкера

    Формула об'єктива використовується для зв'язку радіусів кривизни, товщини, показника заломлення та фокусної відстані товстої лінзи.

    навчальні цілі

    • Порівняйте ідеалізовані тонкі лінзи зі справжніми лінзами

    Рівняння лінзмейкера

    Товсті лінзи

    На відміну від ідеалізованих тонких лінз, справжні лінзи мають кінцеву товщину між двома їх поверхнями кривизни. Ідеальна тонка лінза з двома поверхнями однакової кривизни мала б нульову оптичну силу, а це означає, що вона не сходиться і не розходиться світло. Лінза, товщина якої не незначна, називається товстою лінзою. У цьому випадку ми не можемо просто припустити, що світловий промінь заломлюється лише один раз під час подорожі через об'єктив. Натомість ступінь заломлення повинна залежати від товщини лінзи.

    Лінзи класифікуються за кривизною двох оптичних поверхонь. Лінза двоопукла (або подвійна опукла, або просто опукла), якщо обидві поверхні опуклі. Якщо лінза двоопукла, промінь світла, що рухається паралельно осі лінзи і проходить через об'єктив, буде сходитися (або сфокусований) до плями на осі, на певній відстані позаду об'єктива (тобто фокусна відстань). При цьому лінзу називають позитивною або сходяться лінзою. Див. Діаграму позитивної (сходяться) лінзи.

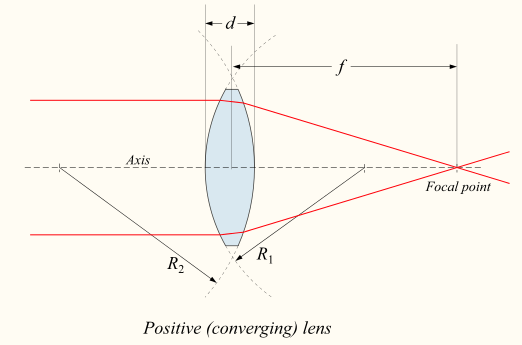
    зображення

    Товста конвергентна лінза: Діаграма позитивної (сходяться) лінзи. Формула об'єктива пов'язує радіуси кривизни, показник заломлення лінзи, товщину лінзи і фокусну відстань.

    Якщо лінза двоувігнута, промінь світла, що проходить через лінзу, розходиться (поширюється); лінзу таким чином називають негативною або розходяться лінзою. Промінь після проходження через лінзу, здається, виходить з певної точки на осі перед лінзою; відстань від цієї точки до лінзи також відома як фокусна відстань, хоча воно негативне щодо фокусної відстані сходяться лінзи. Див. Діаграму негативної (розходяться) лінзи.

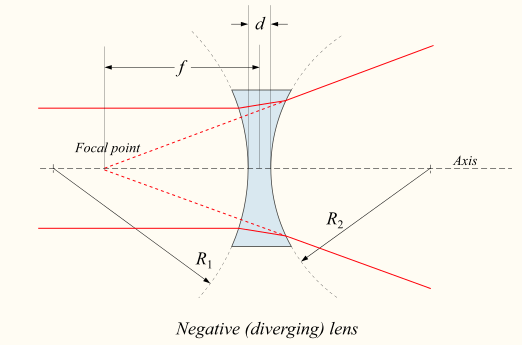
    зображення

    Негативна розбіжна лінза: Діаграма негативної (розбіжної) лінзи. Формула об'єктива пов'язує радіуси кривизни, показник заломлення лінзи, товщину лінзи і фокусну відстань.

    Фокусна відстань товстої лінзи в повітрі можна обчислити за рівнянням лінзмейкера:

    \[\mathrm { P } = \dfrac { 1 } { \mathrm { f } } = ( \mathrm { n } - 1 ) \left[ \dfrac { 1 } { \mathrm { R } _ { 1 } } - \dfrac { 1 } { \mathrm { R } _ { 2 } } + \dfrac { ( \mathrm { n } - 1 ) \mathrm { d } } { \mathrm { nR } _ { 1 } \mathrm { R } _ { 2 } } \right]\]

    де

    • P - потужність об'єктива,
    • f - фокусна відстань об'єктива,
    • n - показник заломлення матеріалу лінзи,
    • R 1 - радіус кривизни поверхні лінзи, найближчої до джерела світла,
    • R 2 - радіус кривизни поверхні лінзи, найвіддаленішої від джерела світла, d і - товщина лінзи (відстань по осі лінзи між двома поверхневими вершинами).

    Угода про знак радіусів R 1 і R 2

    Ознаки радіусів кривизни лінз вказують на те, чи є відповідні поверхні опуклими або увігнутими. Угода про знак, що використовується для представлення цього, змінюється, але для нашого лікування, якщо R 1 позитивний, перша поверхня опукла, а якщо R 1 негативна, поверхня увігнута. Знаки змінюються для задньої поверхні лінзи: якщо R 2 позитивний, поверхня увігнута, а якщо R 2 негативний, поверхня опукла. Якщо будь-який радіус нескінченний, відповідна поверхня рівна. За допомогою цієї конвенції знаки визначаються формами поверхонь лінз і не залежать від напрямку, в якому світло рухається через лінзу.

    Наближення тонкої лінзи

    Вищевказане рівняння можна значно спростити, якщо товщина лінзи d дуже мала в порівнянні з R 1 і R 2. У цьому випадку можна зробити наближення тонкої лінзи, а рівняння лінзоутворювача можна наблизити як

    \[\mathrm { P } = \dfrac { 1 } { \mathrm { f } } \approx ( \mathrm { n } - 1 ) \left[ \dfrac { 1 } { \mathrm { R } _ { 1 } } - \frac { 1 } { \mathrm { R } _ { 2 } } \right]\]

    Фокусна відстань f позитивна для сходяться лінз, а негативна для розходяться лінз. Зворотна фокусна відстань, 1/ f, - оптична лінза. Якщо фокусна відстань в метрах, це дає оптичну потужність в діоптріях (зворотних метрах).

    Лінзи мають таку ж фокусну відстань, коли світло рухається ззаду спереду, як і коли світло йде спереду назад, хоча інші властивості лінзи, такі як аберації, не обов'язково однакові в обох напрямках.

    Заломлення через лінзи

    Оскільки показник заломлення лінзи більший, ніж повітря, промінь рухається до перпендикуляра, коли він входить і відходить, коли він залишає.

    навчальні цілі

    • Порівняйте вплив опуклої лінзи і увігнутої лінзи на світлові промені

    Заломлення через лінзи

    Лінзи зустрічаються у величезному масиві оптичних приладів, починаючи від простого збільшувального скла і закінчуючи об'єктивом камери і закінчуючи об'єктивом людського ока. Слово лінза походить від латинського слова, що позначає сочевицю, форма якої схожа на форму опуклої лінзи (як показано на). Опукла лінза має форму так, щоб всі світлові промені, які потрапляють в неї паралельно її осі, перетинали один одного в одній точці на протилежному боці лінзи. Вісь визначається як лінія, перпендикулярна лінзі в її центрі (як показано на малюнку). Така лінза називається сходяться (або опуклою) лінзою за відповідний вплив, який вона надає на світлові промені. Розширений вигляд шляху одного променя через лінзу ілюструє, як промінь змінює напрямок як при вході, так і при виході з лінзи.

    Так як показник заломлення кришталика більше, ніж у повітря, промінь рухається у напрямку до перпендикуляра при вході, і подалі від перпендикуляра в міру виходу (це відповідно до закону заломлення). Завдяки формі лінзи світло таким чином згинається до осі на обох поверхнях. Точка, в якій промені перетинаються, визначається як фокусна точка F лінзи. Відстань від центру лінзи до її фокусної точки визначається як фокусна відстань f об'єктива. показує, як сходяться лінзи, такі як у збільшувальному склі, можуть концентрувати (сходити) майже паралельні світлові промені від сонця до невеликої плями.

    зображення

    Збільшувальне скло: Сонячне світло, сфокусоване зближуючим збільшувальним склом, може спалити папір. Світлові промені від сонця майже паралельні і перетинаються в фокусній точці лінзи. Чим потужніше лінза, тим ближче до лінзи будуть перетинатися промені.

    Чим більший вплив лінза надає на світлові промені, тим потужніше вона, як кажуть, є. Наприклад, потужна сходяться лінза буде фокусувати паралельні світлові промені ближче до себе і матиме меншу фокусну відстань, ніж слабка лінза. Світло також буде зосереджено на меншому, більш інтенсивному місці для більш потужного об'єктива. Потужність P лінзи визначається як зворотна її фокусна відстань. У формі рівняння:

    \[\mathrm { P } = \dfrac { 1 } { \mathrm { f } }\]

    показує вплив увігнутої лінзи на потрапляють в неї промені світла паралельно її осі (шлях, зроблений променем 2 на малюнку, є віссю лінзи). Увігнута лінза - це розходяться лінза, тому що вона змушує світлові промені відгинатися (розходитися) від своєї осі. У цьому випадку лінза має таку форму, що всі світлові промені, що потрапляють в неї паралельно її осі, здаються походять з тієї ж точки F, визначеної як фокусна точка розбіжної лінзи. Відстань від центру об'єктива до фокусної точки знову називають фокусною відстанню f об'єктива. Зверніть увагу, що фокусна відстань і потужність розходяться лінзи визначаються як негативні. Наприклад, якщо відстань до F в становить 5,00 см, то фокусна відстань f=—5,00 см, а потужність об'єктива - P = —20 D Розширений огляд шляху одного променя через лінзу ілюструє, як форма лінзи (з урахуванням закону заломлення) змушує промінь слідувати своєму конкретному шляху і бути розійшлися.

    У наступних розділах ми розглянемо техніку трасування променів для опису формування зображень лінзами. Крім того, ми вивчимо, як розташування та характеристики зображення можна кількісно визначити за допомогою набору рівнянь геометричної оптики.

    Ключові моменти

    • Коли світло взаємодіє з об'єктами в кілька разів більшими за його довжину хвилі, воно рухається прямими лініями і діє як промінь. Промінь - це просто пряма лінія, яка бере початок в точці.
    • Трасування променів - це метод визначення шляхів, які світло проходить через матерію, наприклад, оптичні системи, що включають лінзи.
    • Тонка лінза визначається як товщина, яка дозволяє променям заломлюватися, як показано на малюнку, але це не дозволяє таким властивостям, як дисперсія та аберації. Ідеальна тонка лінза має дві заломлюючі поверхні, але лінза досить тонка, щоб припустити, що світлові промені згинаються лише один раз.
    • Існує п'ять основних правил трасування променів через лінзу.
    • Трасування променів може бути використано для побудови зображення з променів світла, що походять від об'єкта, що проходить через об'єктив. Зображення розташовується в точці, де перетинаються промені. Вибравши кілька точок з об'єкта, можна побудувати все зображення.
    • Ми визначаємо do, щоб бути відстань об'єкта, відстань об'єкта від центру лінзи. Відстань зображення di визначається як відстань зображення від центру об'єктива. Висота предмета і висота зображення задаються символами ho і hi відповідно.
    • Рівняння тонкої лінзи швидко забезпечує співвідношення між d i, d o та фокусною відстанню f. Він може бути отриманий з геометричного аналізу трасування променів для тонких лінз і дається\(\frac { 1 } { \mathrm { d } _ { \mathrm { o } } } + \frac { 1 } { \mathrm { d } _ { \mathrm { i } } } = \frac { 1 } { \mathrm { f } }\).
    • Збільшення m зображення - це співвідношення між зображенням і висотою об'єкта (h i /h o). Збільшення пов'язане з d o, d i, h o, а h i наступним співвідношенням:\(\frac { \mathrm { h } _ { \mathrm { i } } } { \mathrm { h } _ { \mathrm { o } } } = - \frac { \mathrm { d } _ { \mathrm { i } } } { \mathrm { d } _ { \mathrm { o } } } = \mathrm { m }\).
    • Використання декількох елементів дозволяє корекцію більшої кількості оптичних аберацій, таких як хроматична абберація, викликана залежним від довжини хвилі показником заломлення у склі, ніж це можливо за допомогою однієї лінзи.
    • Якщо лінзи фокусних відстаней f 1 і f 2 «тонкі», комбінована фокусна відстань f лінз задається в\(\frac { 1 } { f } = \frac { 1 } { f _ { 1 } } + \frac { 1 } { f _ { 2 } }\) той час як якщо лінзи розділені деякою відстанню d, то комбінована фокусна відстань задається\(\frac { 1 } { f } = \frac { 1 } { f _ { 1 } } + \frac { 1 } { f _ { 2 } } - \frac { d } { f _ { 1 } f _ { 2 } }\).
    • Якщо відстань поділу дорівнює сумі фокусних відстаней (d = f 1 + f 2), то комбінована фокусна відстань нескінченна. Це відповідає парі лінз, які перетворюють колімований промінь в інший колімований промінь. Цей тип системи називається афокальної системою (простий оптичний телескоп).
    • Ахроматичний дуплет - це свого роду складна лінза, призначена для приведення двох довжин хвиль (зазвичай червоного та синій/фіолетового) у фокусі в одній площині. Це (частково) виправляє хроматичну аберацію, знайдену в одній простій лінзі. Див.
    • Якщо лінза двоопукла, промінь світла, що рухається паралельно осі лінзи і проходить через об'єктив, буде сфокусований до плями на осі, на певній відстані позаду лінзи (тобто фокусна відстань). При цьому лінзу називають позитивною або сходяться лінзою. Див.
    • Якщо лінза двоувігнута, промінь світла, що проходить через лінзу, розходиться (поширюється); таким чином лінзу називають негативною або розбіжною лінзою. Див.
    • Фокусна відстань товстої лінзи в повітрі можна обчислити за рівнянням лінзмейкера:\(\mathrm { P } = \frac { 1 } { \mathrm { f } } = ( \mathrm { n } - 1 ) \left[ \frac { 1 } { \mathrm { R } _ { 1 } } - \frac { 1 } { \mathrm { R } _ { 2 } } + \frac { ( \mathrm { n } - 1 ) \mathrm { d } } { \mathrm { nR } _ { 1 } \mathrm { R } _ { 2 } } \right]\).
    • Ознаки радіусів кривизни лінз вказують на те, чи є відповідні поверхні опуклими або увігнутими. Знаки змінюються для задньої поверхні лінзи: якщо R 2 позитивний, поверхня увігнута, а якщо R 2 негативний, поверхня опукла.
    • Рівняння об'єктива можна значно спростити, якщо товщина лінзи d дуже мала в порівнянні з R 1 і R 2. У цьому випадку можна зробити наближення тонкої лінзи, а рівняння лінзоутворювача можна наблизити як\(P = \frac { 1 } { f } \approx ( n - 1 ) \left[ \frac { 1 } { R _ { 1 } } - \frac { 1 } { R _ { 2 } } \right]\).
    • Нагадаємо, що промінь згинається в міру потрапляння в середовище з іншим показником заломлення. Оскільки показник заломлення лінзи більший, ніж повітря, світловий промінь буде рухатися до перпендикуляра, коли він входить і відходить, коли він залишає.
    • Опукла лінза була сформована так, що всі світлові промені, які потрапляють в неї паралельно її осі, перетинали один одного в одній точці на протилежній стороні лінзи (фокусної точки). Така лінза називається сходяться (або опуклою) лінзою за сходяться ефект, який вона надає на світлові промені. Див.
    • Увігнута лінза - це розходяться лінза, тому що вона змушує світлові промені відгинатися (розходитися) від своєї осі. показує вплив, який вона надає на промені світла, які потрапляють в неї паралельно її осі (шлях, зроблений променем 2 на малюнку, є віссю лінзи).
    • Чим більший вплив лінза надає на світлові промені, тим потужніше вона, як кажуть, є. Потужна сходяться лінза буде фокусувати паралельні світлові промені ближче до себе і матиме меншу фокусну відстань, ніж слабка лінза. Потужність лінзи задається рівнянням\(\mathrm { P } = \frac { 1 } { \mathrm { f } }\).

    Ключові умови

    • фокусна точка: Фокус - точка, в якій сходяться промені світла або іншого випромінювання.
    • трасування променів: метод, що використовується в оптиці для аналізу оптичних систем.
    • тонка лінза: Тонка лінза визначається як така, товщина якої дозволяє променям заломлюватися, але не дозволяє таким властивостям, як дисперсія та аберації.
    • рівняння тонкої лінзи: Відноситься відстань об'єкта do, відстань зображення di та фокусна відстань f:\( \frac { 1 } { \mathrm { d } _ { \mathrm { o } } } + \frac { 1 } { \mathrm { d } _ { \mathrm { i } } } = \frac { 1 } { \mathrm { f } }\)
    • відстань зображення: відстань зображення від центру об'єктива.
    • збільшення: видиме збільшення об'єкта на зображенні.
    • аберація: Зближення до різних вогнищ, лінзою або дзеркалом, променів світла, що виходять з однієї і тієї ж точки, або відхилення таких променів від одного фокусу; дефект механізму фокусування, що перешкоджає передбачуваному фокусному пункту.
    • афокальна система: оптична система, яка не виробляє чистої збіжності або розбіжності променя, тобто має нескінченну ефективну фокусну відстань. Цей тип системи може бути створений за допомогою пари оптичних елементів, де відстань між елементами дорівнює сумі фокусної відстані кожного елемента (d = f1+f2).
    • ахроматичний дуплет: Тип лінзи, що складається з двох простих об'єктивів, спарених разом, розроблених таким чином, що хроматична аберація кожної лінзи частково компенсує іншу; таким чином світло в діапазоні довжин хвиль може бути доведено до того ж фокусу.
    • товста лінза: лінзи, товщина яких не незначна (тобто не можна зробити просте припущення, що світловий промінь заломлюється лише один раз в лінзі).
    • вершини поверхні: точки, де кожна поверхня перетинає оптичну вісь. Вони важливі насамперед тому, що вони є фізично вимірними параметрами положення оптичних елементів, і тому положення інших кардинальних точок повинні бути відомі щодо вершин для опису фізичної системи.
    • опукла лінза: лінза, що має принаймні одну опуклу поверхню, така, що світло, що проходить через неї, може бути доведено до фокусу.
    • увігнута лінза: лінза, що має принаймні одну увігнуту поверхню, так що промені світла, що проходять через неї, відгинаються від її оптичної осі.

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ