5.2: Принцип еквівалентності

Last updated
Save as PDF

Page ID: 77390

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Поясніть принцип еквівалентності

Еквівалентність прискорення гравітаційному полю

Неіснування FloatyStuff у нашому Всесвіті є окремим випадком принципу еквівалентності. Принцип еквівалентності стверджує, що прискорення (наприклад, прискорення літаючої тарілки) завжди еквівалентно гравітаційному полю, і жодне спостереження ніколи не може сказати різницю без посилання на щось зовнішнє. (І припустимо, у вас була якась зовнішня точка відліку - як би ви знали, чи прискорюється вона?)

Експерименти Eötvös

FloatyStuff був би крайнім прикладом, але якби було якесь порушення універсальності вільного падіння, яким би маленьким не було, то принцип еквівалентності був би фальсифікований. З часів Галілея експериментальні методи мали кілька століть, в яких можна було вдосконалити, а другий закон піддався подібним випробуванням з експоненціально покращувальною точністю. Для такого експерименту в 1993 році ¹ фізик Пізанського університету (!) побудував металевий диск з міді та вольфраму півкіл, з'єднаних між собою на плоских краях. Вони евакуювали повітря з вертикального вала і скинули диск вниз його\(142\) раз, використовуючи лазери для вимірювання будь-якого крихітного обертання, яке призвело б, якби прискорення міді та вольфраму були дуже дещо різними. Результати були статистично узгоджені з нульовим обертанням і ставили верхню межу\(1×10^{-9}\) на дробову різницю в прискоренні.

\[\frac{ |g_{copper} - g_{tungsten}|}{g}\]

Експерименти такого типу називаються експериментами Eötvös, після Лорана Етвеша, який зробив перші сучасні, високоточні версії.

рис. 5.2.1.png — Ілюстрація\(\PageIndex{1}\): Лоран Етвеш (1848-1919).

Приклад\(\PageIndex{1}\): The artificial horizon

рис. 5.2.2.png — Малюнок\(\PageIndex{2}\): Штучний горизонт.

Пілот літака не завжди може легко сказати, який шлях вгору. Горизонт може бути не рівним просто тому, що земля має фактичний нахил, і в будь-якому випадку горизонт може бути не видно, якщо погода туманна. Можна уявити, що проблему можна вирішити просто повісивши маятник і спостерігаючи, в який бік він вказував, але за принципом еквівалентності маятник не може визначити різницю між гравітаційним полем і прискоренням літака відносно землі - як і будь-який інший акселерометр, такі як внутрішнє вухо пілота. Наприклад, коли літак повернеться вправо, акселерометри будуть обманом вважати, що «вниз» вниз і вліво. Щоб обійти цю проблему, літаки використовують пристрій під назвою штучний горизонт, який по суті є гіроскопом. Гіроскоп повинен бути ініціалізований, коли площина, як відомо, орієнтована в горизонтальній площині. Жоден гіроскоп не ідеальний, тому з часом він буде дрейфувати. З цієї причини прилад також містить акселерометр, а гіроскоп автоматично відновлюється до узгодження з акселерометром, з постійною часом кілька хвилин. Якщо площину обтікати колами протягом декількох хвилин, штучний горизонт буде обдурити, вказуючи на те, що неправильне напрямок вертикальне.

Гравітація без гравітації

Ми живемо зануреними в земне гравітаційне поле, і саме тут ми проводимо майже всі наші експерименти з фізики. Дивно, що спеціальна відносність може бути підтверджена в земних експериментах, іноді з феномональною точністю, як у тесті\(10\) значної фігури експерименту Айвза-Стілвелла релятивістського рівняння доплерівського зсуву. Як це може бути, оскільки спеціальна відносність повинна бути версією відносності, яка не може впоратися з гравітацією? Принцип еквівалентності дає відповідь. Якщо єдиний гравітаційний вплив на ваш експеримент - це рівномірне поле\(g\), то це справедливо для вас, щоб описати свій експеримент як зроблений у регіоні без будь-якої гравітації, але в лабораторії, підлога якої, як трапилося, прискорюється вгору з прискоренням\(-g\). Спеціальна теорія відносності працює просто чудово в таких ситуаціях, тому що перемикання в прискорену систему відліку не впливає на плосність простору-часу. Зауважте, що гравітаційний зонд B обертався навколо землі, тому поле, яке він переживав, змінювалося за напрямком, що призвело до невдачі вищезгаданого аргументу; ефекти, які він спостерігав, не були пояснені особливою відносністю.

Гравітаційні доплерівські зрушення

рис. 5.2.3.png — Малюнок\(\PageIndex{3}\): 1. З поверху ліфта вгору випромінюється легка хвиля. Ліфт розганяється вгору. До моменту виявлення світлової хвилі на стелі ліфт змінив свою швидкість, тому хвиля виявляється з доплерівським зсувом.

Для прикладу конкретно гравітаційного експерименту, який можна пояснити спеціальною відносністю, і це насправді було проведено, У лабораторії, що прискорюється вгору, світлова хвиля, що випромінюється з підлоги, буде доплерівська зміщена до нижчих частот, коли спостерігаються на стелі, через зміну у швидкості приймача під час польоту хвилі. Ефект дає

\[\frac{\Delta f}{f} \approx \frac{-a\Delta x}{c^2}\]

де a - прискорення лабораторії,\(∆x\) це висота від підлоги до стелі, і\(c\) швидкість світла.

У одиницях с\(c = 1\), у нас є

\[\frac{\Delta f}{f} \approx -a\Delta x\]

За принципом еквівалентності ми знаходимо, що коли такий експеримент проводиться в гравітаційному полі\(g\), має бути гравітаційний вплив на частоту

\[\frac{\Delta f}{f} \approx -g\Delta x\]

Це можна виразити більш компактно, як

\[\frac{\Delta f}{f} \approx -\Delta \Phi\]

де\(Φ\) - гравітаційний потенціал, тобто гравітаційна енергія на одиницю маси.

рис. 5.2.4.png — Малюнок\(\PageIndex{4}\): Фунт і Ребка у верхній і нижній частині вежі.

У 1959 році Паунд і Ребка ² провели експеримент у вежі в Гарварді. Гамма-промені з випромінювалися\(^{57}\textrm{Fe}\) джерелом внизу і виявлялися вгорі, піднявшись\(∆x = 22.6 m\). Принцип еквівалентності прогнозує дробовий зсув частоти внаслідок сили тяжіння\(2.46×10^{-15}\). Це дуже мало, і, як правило, маскувалося б ефектами віддачі, але, використовуючи ефект Мессбауера Фунт і Ребка виміряли зсув бути\((2.56±0.25)×10^{-15}\).

Мінлива метрика

В експерименті «Фунт-Ребка» ядра, що випромінюють гамма-промені на частоті,\(f\) можна розглядати як маленькі годинники. Кожен гребінь хвилі, який поширюється вгору, - це сигнал, який говорить про те, що годинник один раз поставили галочку. Спостерігач у верхній частині вежі виявляє, що сигнали надходять на нижчій частоті\(f'\), і природно робить висновок, що годинник внизу були сповільнені через якийсь ефект розширення часу, що виникає внаслідок гравітації.

Це може здатися великим концептуальним стрибком, але це було підтверджено за допомогою атомних годин. У експерименті 1978 року Іджіма та Фудзівара, фігура\(\PageIndex{5}\), ідентичні атомні годинники зберігалися у спокої у верхній та нижній частині гори поблизу Токіо. Розбіжності між годинниками узгоджувалися з прогнозами принципу еквівалентності. Гравітаційний доплерівський зсув також був одним з ефектів, який призвів до ненульового результату експерименту Хафеле-Кітінга, в якому атомні годинники літали по всьому світу на борту комерційних пасажирських літаків. Кожен раз, коли ви використовуєте систему GPS, ви використовуєте ці ефекти.

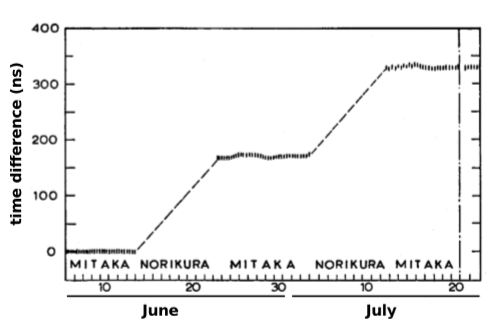
рис 5.2.5.png — Малюнок\(\PageIndex{5}\): Графік, що показує різницю в часі між двома атомними годинами. Один годинник зберігався в обсерваторії Мітака, на висоті 58 м над рівнем моря. Інший був переміщений туди-сюди до другої обсерваторії, станції Norikura Corona, на піку вулкана Норікура, 2876 м над рівнем моря. Плато на графіку - це дані періодів, коли годинник порівнювали пліч-о-пліч у Мітака. Різниця між одним плато і наступним показує гравітаційний вплив на швидкість течії часу, накопичену в період, коли мобільний годинник знаходився на вершині Норікура.

Починаючи тільки з, здавалося б, нешкідливого припущення принципу еквівалентності, ми приводимо до дивно далекосяжних висновків. Ми знаходимо, що час тече з різною швидкістю залежно від висоти в гравітаційному полі. Оскільки метрику можна інтерпретувати як міру кількості належного часу уздовж заданої світової лінії, то робимо висновок, що ми не завжди можемо виразити метрику в звичній формі\(\tau ^2 = (+1)\Delta t^2 + (-1)\Delta x^2\) з фіксованими коефіцієнтами\(+1\) і\(-1\). Припустимо, що\(t\) координата визначається радіосинхронізацією. Потім\(+1\) в метриці потрібно замінити на приблизно\(1 + 2Φ\), де ми приймаємо\(Φ = 0\) за умовністю на висоті стандартних годин, які координують синхронізацію.

Майте на увазі, що хоча ми підключили гравітацію до вимірювального апарату спеціальної відносності, немає кривизни просторучасу, тому те, що ми робимо тут, все ще є особливою відносністю, а не загальною відносністю. Насправді тут немає нічого більш загадкового, ніж перейменування подій простору-часу через зміну координат. Перейменування може бути зручним, якби ми використовували наземні опорні точки для вимірювання\(x\) координат. Але якби ми відчували, що це так, ми могли б перейти на хорошу інерційну систему відліку, яка була вільно падаючою. У цьому кадрі ми отримали б точно такий же прогноз для результатів будь-якого експерименту. Наприклад, спостерігач із вільним падінням пояснив би результат експерименту «Фунт-Ребка», що виникає внаслідок висхідного прискорення детектора подалі від джерела.

Посилання

¹ Carusotto et al., «Обмеження на порушення g-універсальності з експериментом Галілеотипу», Phys Lett A183 (1993) 355. Вільно доступний в Інтернеті за адресою researchgate.net.

² Фіз. Преподобний Літт. 4 (1960) 337