1.6: Принцип еквівалентності (частина 2)
- Page ID
- 77633
Гравітаційні червоні зрушення
Раніше ми бачили експериментальні докази того, що швидкість течії часу змінюється з висотою в гравітаційному полі. Тепер ми бачимо, що цього вимагає принцип еквівалентності.
За принципом еквівалентності немає можливості визначити різницю між експериментальними результатами, отриманими в прискорювальній лабораторії, та результатами, знайденими в лабораторії, зануреної в гравітаційне поле. 30 У лабораторії, що прискорюється вгору, фотон випромінюється з підлоги і буде зміщений доплером до нижчих частот при спостереженні на стелі, через зміну швидкості приймача під час польоту фотона. Ефект дає
\[\dfrac{\Delta E}{E} = \dfrac{\Delta f}{f} = \dfrac{ay}{c^{2}}\]
де\(a\) - прискорення лабораторії,\(y\) це висота від підлоги до стелі, і\(c\) швидкість світла.
Примітка
Завдання 4 перевіряє в одному конкретному прикладі, що такий спосіб встановлення принципу еквівалентності мається на увазі той, який був заявлений раніше.
Вправа\(\PageIndex{1}\)
Самостійна перевірка: Перевірте це твердження.
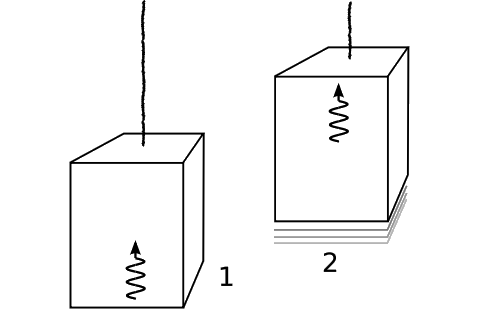
За принципом еквівалентності ми знаходимо, що при проведенні такого експерименту в гравітаційному полі g має відбуватися гравітаційний вплив на енергію фотона, рівну\(\frac{\Delta E}{E} = \frac{gy}{c^{2}}\). Оскільки величина gy - гравітаційний потенціал (гравітаційна енергія на одиницю маси), то дробові втрати енергії фотона такі ж, як (ньютонівська) втрата енергії, яку відчуває матеріальний об'єкт маси m і початкова кінетична енергія mc 2.
Тлумачення виглядає наступним чином. Класичний електромагнетизм вимагає, щоб електромагнітні хвилі мали інерцію. Наприклад, якщо плоска хвиля вражає омічну поверхню, як на малюнку 1.5.14, електричне поле хвилі збуджує коливальні струми в поверхні. Потім ці струми відчувають магнітну силу від магнітного поля хвилі, і застосування правого правила показує, що результуюча сила знаходиться в напрямку поширення хвилі. Таким чином, світлова хвиля діє так, ніби вона має імпульс. Принцип еквівалентності говорить, що все, що має інерцію, також повинно брати участь у гравітаційних взаємодіях. Тому легкі хвилі повинні мати вагу, і повинні втрачати енергію, коли вони піднімаються через гравітаційне поле.
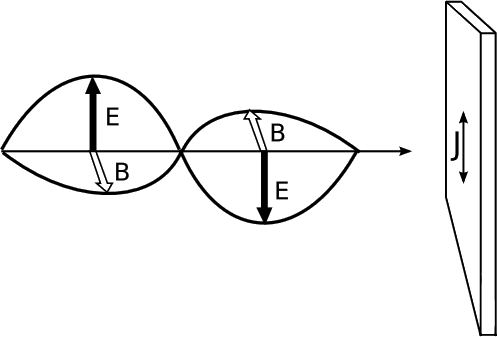
Вправа\(\PageIndex{2}\)
Самостійна перевірка: Перевірте застосування правила правої руки, описаного вище.

Подальше тлумачення:
- Кількість\(mc^2\) відома, навіть серед людей, які не знають, що\(m\) і\(c\) стоять за. Це перший натяк на те, звідки він береться. Повний розповідь наведено в розділі 4.2.
- Співвідношення p =\(\frac{E}{c}\) між енергією та імпульсом світлової хвилі випливає безпосередньо з рівнянь Максвелла, за аргументом вище; однак у розділі 4.2 ми побачимо, що відповідно до відносності це відношення повинно триматися для будь-якої безмасової частинки
- Те, що ми знайшли, узгоджується з принципом відповідності Нільса Бора, який стверджує, що коли нова фізична теорія, така як відносність, замінює стару, таку як фізика Ньютона, нова теорія повинна погодитися зі старою в експериментальних умовах, в яких стара теорія була перевірена експерименти. Гравітаційна маса пучка світла з енергією\(E\) є\(\frac{E}{c^{2}}\), а оскільки c - велика кількість, не дивно, що вага світлових променів ніколи не був виявлений до того, як Ейнштейн намагався його виявити.
- У цій книзі описується одна конкретна теорія гравітації, теорія загальної відносності Ейнштейна. Існують і інші теорії гравітації, і деякі з них, такі як теорія Бренса-Діка, роблять так само добре, як і загальна теорія відносності, узгоджуючись з наявними в даний час експериментальними даними. Наше прогнозування гравітаційних доплерівських зрушень світла залежало лише від принципу еквівалентності, який є одним із складових загальної теорії відносності. Експериментальні тести цього прогнозу перевіряють лише принцип еквівалентності; вони не дозволяють нам розрізняти одну теорію гравітації та іншу, якщо обидві теорії включають принцип еквівалентності.
- Якщо такий об'єкт, як радіопередавач або атом в збудженому стані випромінює електромагнітну хвилю з частотою f, то об'єкт можна вважати типом годинника. Тому ми можемо інтерпретувати гравітаційний червоний зсув як розширення гравітаційного часу: різницю в швидкості, з якою протікає сам час, залежно від гравітаційного потенціалу. Це узгоджується з емпіричними результатами, представленими в розділі 1.2.
Приклад 3: Парадокс Чіао переглянуто
Принцип еквівалентності говорить, що електромагнітні хвилі мають гравітаційну масу, а також інерційну масу, тому здається зрозумілим, що те саме повинно триматися для статичних полів. У парадоксі Чіао орбітальна заряджена частинка має електричне поле, яке поширюється до нескінченності. Коли ми вимірюємо масу зарядженої частинки, такої як електрон, немає можливості відокремити масу цього поля від більш локалізованого внеску. Електричне поле «падає» через гравітаційне поле, і принцип еквівалентності, який є локальним, не може гарантувати, що всі частини поля обертаються рівномірно навколо землі навіть у віддалених частинок Всесвіту. Схема електричного поля спотворюється, і це спотворення викликає реакцію випромінювання, яка назад реагує на частинку, викликаючи її орбіту розпаду.
Експеримент «Фунт-Ребка»
Експеримент «Фунт-Ребка» 1959 року в Гарварді 31 був одним з перших високоточних, релятивістських тестів принципу еквівалентності, які проводилися в контрольованих умовах, і в цьому розділі ми детально його обговоримо.
Коли y знаходиться на порядку висоти будівлі, значення\(\frac{\Delta E}{E} = \frac{gy}{c^{2}}\) дорівнює 10 −14, тому для виявлення гравітаційного червоного зсуву необхідний надзвичайно точний експеримент. Ряд інших ефектів досить великі, щоб затемнити його повністю, і їх потрібно якось усунути або компенсувати. Вони перераховані нижче, разом з їх порядками в експериментальному дизайні, нарешті, оселився на фунті і Ребці.
| (1) Класичне доплерівське розширення через температуру. Тепловий рух викликає доплерівські зрушення випромінюваних фотонів, що відповідають випадковій складовій вектора швидкості випромінюючого атома вздовж напрямку випромінювання. | ✔ 10 −6 |
| (2) Віддача доплерівського зсуву. Коли атом випромінює фотон з енергією Е та імпульсом\(p = \frac{E}{c}\), збереження імпульсу вимагає віддачі атома з імпульсом\(p = − \frac{E}{c}\) та енергією\(\frac{p^{2}}{2m}\). Це викликає доплерівський зсув енергії випромінюваного фотона вниз. Подібний вплив відбувається і на абсорбцію, подвоюючи проблему. | ✔ 10 −12 |
| (3) Природна ширина лінії. Принцип невизначеності Гейзенберга говорить, що стан з періодом напіврозпаду\(\tau\) повинен мати невизначеність у своїй енергії щонайменше\(\frac{h}{\tau}\), де h - константа Планка. | ✔ 10 −12 |
| (4) Спеціально-релятивістський доплерівський зсув через температуру. У розділі 1.2 представлені експериментальні докази того, що час тече з різною швидкістю в залежності від руху спостерігача. Тому тепловий рух атома, що випромінює фотон, впливає на частоту фотона, навіть якщо рух атома не вздовж лінії випромінювання. Рівняння, необхідні для обчислення цього ефекту, не будуть виведені до розділу 2.2; кількісна оцінка наведена в прикладі 13. Наразі нам потрібно лише знати, що це призводить до температурної залежності середньої частоти випромінювання, крім розширення кривої дзвінка, описаного вище ефектом (1). | ✔ 10 −14 на градус С |
Найпростішим способом пом'якшення ефекту (1) є використання фотонів, що випромінюються з твердого тіла. На перший погляд це здавалося б поганою ідеєю, оскільки електрони в твердому тілі випромінюють безперервний спектр світла, а не дискретний спектр, як ті, що випромінюються газами; це тому, що у нас є N електронів, де N знаходиться в порядку числа Авогадро, всі вони сильно взаємодіють один з одним, тому принцип відповідності дискретна квантово-механічна поведінка повинна бути усереднена. Але протони та нейтрони в межах одного ядра взагалі не взаємодіють з тими, що знаходяться в інших ядрах, тому фотони, що випромінюються ядром, мають дискретний спектр. Енергетична шкала ядерних збуджень знаходиться в діапазоні кеВ або МеВ, тому ці фотони є рентгенівськими або гамма-променями. Крім того, часові масштаби випадкових коливань ядра в твердому тілі надзвичайно короткі. Для швидкості близько 100 м/с і коливань з амплітудою 10 −10 м час становить близько 10 −12 с У багатьох випадках це набагато коротше, ніж період напіврозпаду збудженого ядерного стану, що випромінює гамма-промінь, і тому доплерівський зсув в середньому майже до нуля.

Ефект (2) все ще набагато більший за розмір ефекту 10 −14, який потрібно виміряти. Його можна уникнути, використовуючи ефект Мессбауера, при якому ядро в твердій речовині при низькій температурі випромінює або поглинає гамма-фотон, але зі значною ймовірністю віддача береться не окремим ядром, а вібрацією атомної решітки в цілому. Оскільки енергія віддачі змінюється як\(\frac{p^{2}}{2m}\), то велика маса решітки призводить до дуже невеликого розсіювання енергії в відкатну решітку. Таким чином, якщо фотон випромінюється і поглинається однаковими ядрами в твердому тілі, а як для емісії, так і для поглинання імпульс віддачі приймається решіткою в цілому, то відбувається мізерно малий зсув енергії. Потрібно підібрати ізотоп, який випромінює фотони з енергіями близько 10-100 кеВ. Рентгенівські промені з енергіями нижче приблизно 10 кеВ, як правило, сильно поглинаються речовиною і їх важко виявити, тоді як для енергій гамма-випромінювання\(\gtrsim\) 100 кеВ ефект Моссбауера недостатньо для усунення ефекту віддачі повністю.
Якщо ефект Мессбауера здійснюється в горизонтальній площині, відбувається резонансне поглинання. Коли джерело і поглинач вирівняні по вертикалі, р, гравітаційні зсуви частоти повинні викликати невідповідність, руйнуючи резонанс. Можна переміщати джерело з невеликою швидкістю (зазвичай кілька мм/с), щоб додати доплерівський зсув на частоту; визначаючи швидкість, яка компенсує гравітаційний ефект, можна визначити, наскільки великий гравітаційний ефект.
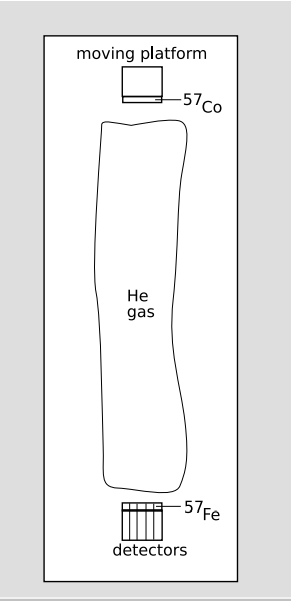
Типовий період напіврозпаду для дезбудження ядра випромінюванням гамма-випромінювання енергією Е знаходиться в наносекундному діапазоні. Щоб виміряти гравітаційний ефект на рівні 10 −14, потрібно мати природну ширину лінії (3) з\(\frac{\Delta E}{E}\)\(\lesssim\) 10 −14, для чого потрібен період напіврозпаду\(\gtrsim\) 10\(\mu\) с. На практиці Паунд і Ребка виявили, що інші ефекти, такі як (4) та електрон- Взаємодія ядер, яка залежала від підготовки зразка, мала тенденцію ставити ядра в одному зразку «не співзвучно» з тими, що знаходяться в іншому зразку на рівні 10 −13 -10 −12, так що резонанс не може бути досягнутий, якщо природна ширина лінії не давала\(\frac{\Delta E}{E} \gtrsim\) 10 −12. В результаті вони влаштувалися на експеримент, в якому 14 кеВ гамми випромінювалися 57 ядрами Fe (рис. 1.5.17) у верхній частині 22-метрової вежі, а внизу поглиналися ядрами 57 Fe. 100-ns період напіввиведення збудженого стану призводить\(\frac{\Delta E}{E}\) до 10 −12. Це в 500 разів більше, ніж гравітаційний ефект, який потрібно виміряти, тому, як описано більш детально нижче, експеримент залежав від високоточних вимірювань малих зсувів вгору-вниз резонансної кривої у формі дзвону.
Поглиначі представляли собою сім залізних плівок, ізотопічно посилених у 57 Fe, нанесених безпосередньо на грані семи детекторів сцинтиляції йодиду натрію (внизу рисунка 1.5.16). Коли гамма-випромінювання потрапляє на поглиначі, може статися ряд різних речей, з яких ми можемо піти, враховуючи лише наступне: (а) гамма-промінь резонансно поглинається в одному з поглиначів 57 Fe, після чого збуджене ядро розпадається шляхом повторного випромінювання іншого такого фотона (або перетворення електрона), у випадковому напрямку; (б) гамма-промінь проходить через поглинач, а потім виробляє іонізацію безпосередньо в кристалі йодиду натрію. У випадку б виявляється гамма-випромінювання. У випадку a існує 50% ймовірність того, що повторно випромінюваний фотон вийде у напрямку вгору, так що його неможливо виявити. Таким чином, коли умови підходять для резонансу, очікується зниження швидкості підрахунку. Ефект Моссбауера ніколи не відбувається зі 100% ймовірністю; в цьому експерименті близько третини гамми, що падають на поглиначі, були резонансно поглинені.
Вибір y = 22 м був продиктований в основному систематичними похибками. Експеримент був обмежений силою джерела гамма-випромінювання. Для джерела фіксованої сили швидкість підрахунку в детекторі на відстані y буде пропорційною y −2, що призводить до статистичних похибок, пропорційних\(1/ \sqrt{count\; rate} \propto y\). Оскільки ефект, який потрібно вимірювати, також пропорційний y, співвідношення сигнал/шум було незалежним від y Однак систематичні ефекти, такі як (4), легше відстежувати та враховувати, коли y був досить великим. Будівля лабораторії в Гарварді мала 22-метрову вежу, яка використовувалася для експерименту. Для зменшення поглинання гамми в 22 метрах повітря в шахті був поміщений довгий циліндричний міларовий мішок, повний гелієвого газу, стор.
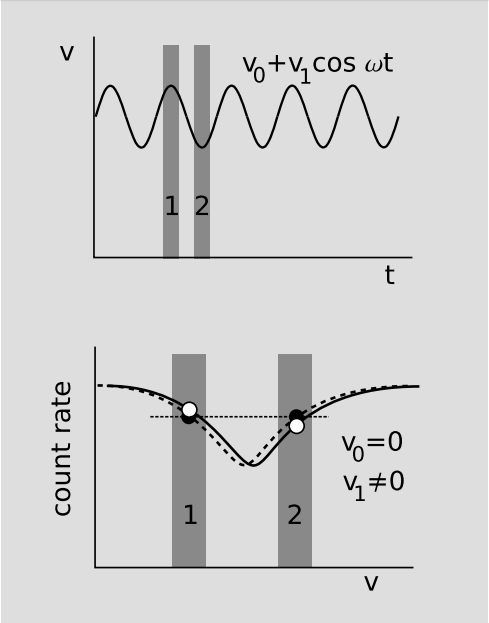
Резонанс представляв собою дзвіноподібну криву з мінімумом на власній частоті випромінювання. Оскільки крива була на мінімумі, де її похідна дорівнювала нулю, чутливість швидкості підрахунку до гравітаційного зсуву була б майже нульовою, якби джерело було нерухомим. Тому потрібно було вібрувати джерело вгору-вниз, щоб випромінювані фотони були доплеровскіе зміщені на плечі резонансної кривої, де нахил кривої був великим. Отримана асиметрія в показниках підрахунку показана на малюнку 1.5.18. Подальші зусилля щодо скасування можливих систематичних ефектів були зроблені шляхом частого перемикання джерела та поглинача між верхньою та нижньою частинами вежі.
Для y = 22,6 м принцип еквівалентності прогнозує дробовий зсув частоти внаслідок сили тяжіння 2,46 × 10 −15. Фунт і Ребка виміряли зсув, щоб бути (2,56 ± 0,25) × 10 −15. Результати були в статистичному узгодженні з теорією і перевіряли прогнозований розмір ефекту з точністю до 10%.

Малюнок\(\PageIndex{19}\) - Фунт і Ребка у верхній і нижній частині вежі.
Посилання
31 Фіз. Преподобний Літт. 4 (1960) 337
