1.5: Принцип еквівалентності (частина 1)

Пропорційність інерційної та гравітаційної маси

Яку фізичну інтерпретацію слід дати «лініям», описаним у впорядкованій геометрії? Галілей описав експеримент (який він, можливо, і не виконав насправді), в якому він одночасно скинув гарматне ядро і мушкетний м'яч з високої вежі. Два об'єкти потрапили в землю одночасно, спростовуючи твердження Аристотеля про те, що предмети падали зі швидкістю, пропорційною їх вазі. На графіку простору-часу з осями x і t криві, простежувані двома об'єктами, які називаються їх світовими лініями, є ідентичними параболами. (Шляхи кульок через простір x − y − z прямі, а не вигнуті.) Один із способів пояснення цього спостереження полягає в тому, що те, що ми називаємо «масою», насправді є двома окремими речами, які трапляються рівними. Інерційна маса, яка фігурує в a = Ньютона\(\frac{F}{m}\), описує, наскільки важко прискорити об'єкт. Гравітаційна маса описує силу, з якою діє гравітація. Гарматне ядро має в сто разів більше гравітаційної маси, ніж мушкетний м'яч, тому сила тяжіння, що діє на нього, в сто разів більше. Але його інерційна маса також точно в сто разів більше, тому два ефекти скасовуються, і він падає з тим же прискоренням. Це особлива властивість гравітаційної сили. Електричні сили, наприклад, так не поводяться. Сила, яку відчуває об'єкт в електричному полі, пропорційна його заряду, який не пов'язаний з його інерційною масою, тому різні заряди, розміщені в одному електричному полі, взагалі матимуть різні рухи.

Малюнок\(\PageIndex{1}\) - Гарматне ядро і мушкетбол мають однакові параболічні світові лінії. На цьому типі просторово-часового сюжету простір умовно показано на горизонтальній осі, тому вежу доводиться зображувати на її стороні.

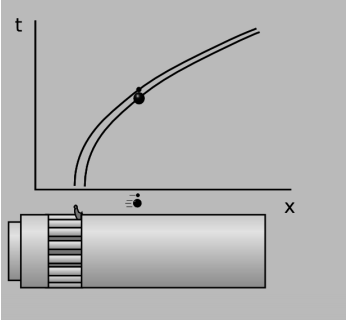
Геометрична обробка гравітації

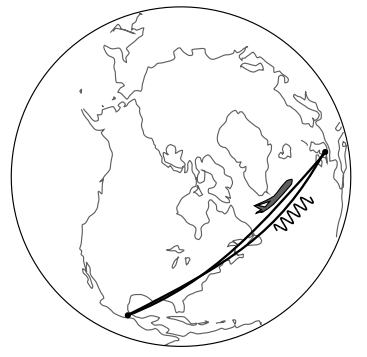
Ейнштейн зрозумів, що це особлива властивість гравітаційної сили дозволило описати гравітацію в чисто геометричному вираженні. Визначено світові лінії малих об'єктів ⁹, що діють під дією сили тяжіння, як лінії, описані аксіомами геометрії. Оскільки ми зазвичай думаємо про «лінії», описані евклідовою геометрією та її родичами, як прямі, це означає переосмислення того, що означає пряма лінія. За аналогією, уявіть, що розтягуєте шматок струни, натягнутий по всій земній кулі, як ми могли б зробити для того, щоб спланувати політ літака або націлити спрямовану радіоантену. Струна не може здаватися прямою, як видно з тривимірного евклідового простору, в якому вбудований земна куля, але вона максимально пряма в тому сенсі, що це шлях, за яким слідує радіохвиля, ¹⁰ або пілот літака, який тримає рівень крил і кермо прямо. Світ- «лінія» об'єкта, на яку діють негравітаційні сили, не вважається прямою «лінією» в розумінні O1-O4. При необхідності цю неоднозначність в перевантаженому терміні «лінія» усувають, посилаючись на лінії О1-О4 як геодезичні. Світова лінія маломасового об'єкта, на яку діяла тільки гравітація, є одним з видів геодезичних. ¹¹

Малюнок\(\PageIndex{2}\) - Шматок струни, натягнутий на земній кулі, утворює геодезичний від Мехіко до Лондона. Хоча він виглядає вигнутим, він є аналогом прямої лінії в неевклідової геометрії, обмеженої поверхнею Землі. Подібним чином світові лінії фігури а виглядають вигнутими, але вони є аналогами прямих ліній в неевклідовій геометрії, що використовуються для опису гравітаційних полів у загальній теорії відносності.

Нотатки

⁹ Причиною обмеження на дрібні об'єкти по суті є гравітаційне випромінювання. Об'єкт також повинен бути електрично нейтральним, і ні об'єкт, ні навколишній простор не повинні містити ніяких екзотичних форм негативної енергії. Про це більш детально мова далі. Див. також проблему 1.

¹⁰ Радіохвилі в діапазоні ВЧ, як правило, потрапляють у пастку між землею та іоносферою, змушуючи їх кривитися над горизонтом, дозволяючи міжміський зв'язок.

¹¹ Докладніше обґрунтування цього твердження див. Розділ 9, завдання 1.

Тепер ми можемо побачити глибоку фізичну важливість заяви O1, що дві події визначають лінію. Щоб передбачити траєкторію польоту м'яча для гольфу, нам потрібно мати деякі вихідні дані. Наприклад, ми могли б виміряти подію А, коли м'яч розриває контакт з клубом, і подія B нескінченно малий час після А. ¹² Цю пару спостережень можна розглядати як фіксацію початкового положення та швидкості м'яча, яких повинно бути достатньо для прогнозування унікальної світової лінії для м'яча, оскільки відносність - детермінована теорія. За допомогою цієї інтерпретації ми також можемо зрозуміти, чому це не обов'язково катастрофа для теорії, якщо O1 іноді виходить з ладу. Наприклад, подія А може означати запуск двох супутників на кругові орбіти з одного і того ж місця на Землі, що прямують в протилежних напрямках, а B могло бути їх подальшим зіткненням на протилежному боці планети. Хоча це порушує O1, це не порушує детермінізму. Детермінізм вимагає лише дійсності O1 для подій нескінченно близьких один до одного. Навіть для випадково обраних подій далеко один від одного, ймовірність того, що вони порушать O1, дорівнює нулю.

Малюнок\(\PageIndex{3}\) - Якщо геодезичні дані, визначені літаком і радіохвилею, відрізняються один від одного, то лікувати обидві проблеми точно, використовуючи одну і ту ж геометричну теорію, не представляється можливим. Загалом відносність, це було б аналогічно порушенню принципу еквівалентності. Обґрунтованість загальної теорії відносності як чисто геометричної теорії гравітації вимагає, щоб принцип еквівалентності був точно задоволений у всіх випадках.

Примітка

Щодо нескінченності, див. Приклад 3.

Експерименти Eötvös

Вся система Ейнштейна руйнується, якщо є якесь порушення, яким би маленьким не було, пропорційності між інерційною і гравітаційною масою, і тому експериментальним шляхом шукати подібне порушення стає дуже цікаво. Наприклад, ми можемо задатися питанням, чи мали нейтрони та протони дещо інші співвідношення гравітаційної та інерційної маси, що в експерименті в стилі Галілео спричинить невелику різницю між прискоренням свинцевої ваги з великим співвідношенням нейтрон-протон та дерев'яним, який складається з світла елементи з майже рівною кількістю нейтронів і протонів. Перші високоточні експерименти цього типу були проведені Етвесом приблизно на рубежі ХХ століття, і вони перевірили еквівалентність інерційної та гравітаційної маси приблизно до однієї частини в 10 ⁸. Вони, як правило, називають експериментами Eötvös.

Ілюстрація\(\PageIndex{4}\): Лоран Етвеш (1848-1919).

На малюнку 1.5.5 нижче показана стратегія проведення експериментів Eötvös, які дозволили тест приблизно на одну частину в 10 ¹². Верхня панель - спрощений варіант. Платформа збалансована, тому гравітаційні маси двох об'єктів спостерігаються рівними. Предмети виготовлені з різних речовин. Якщо еквівалентність інерційної та гравітаційної маси не зможе утримуватися для цих двох речовин, то сила тяжіння на кожній масі не буде точно пропорційною її інерції, і платформа буде відчувати невеликий крутний момент, коли земля крутиться.

Малюнок _1.5.5b.png» />

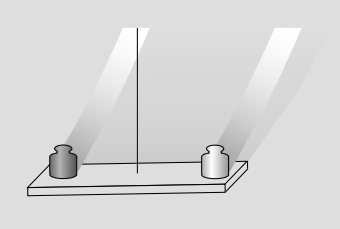
Малюнок\(\PageIndex{5}\): Експеримент Eötvös. Топ: спрощений варіант. Знизу: реалістична версія Брагінського і Панова. (Малюнок по Брагінському і Панова.)

На нижній панелі зображений більш реалістичний малюнок експерименту Брагінського і Панова. ¹³ Все це було укладено у високу вакуумну трубку, яка була поміщена в герметичний підвал, температура якого контролювалася в межах 0,02° C. загальна маса платинових і алюмінієвих тестових мас, плюс вольфрамовий дріт і балансир, становила всього 4,4 м Для виявлення крихітних рухів лазерний промінь відскочив від дзеркала, прикріпленого до дроту. Там було так мало тертя, що баланс прийняв би порядку декількох років, щоб повністю заспокоїтися після введення на місце; щоб зупинити ці вібрації, статичні електричні сили були застосовані через дві кругові пластини, щоб забезпечити дуже ніжні повороти на еліпсоїдній масі між ними.

За 45 років з часу роботи Брагінського і Панова були внесені вдосконалення в більш прямих експериментальних випробуваннях принципу еквівалентності, при якому тестові маси просто вільно падають. Найкращий земний експеримент цього типу ¹⁴ дав зв'язок 10 ⁻⁹, тоді як новий експеримент на орбіті ¹⁵ посилив це значення до 10 ⁻¹⁴.

Еквівалентність гравітаційних полів і прискорень

Одним із наслідків нульових результатів експериментів Етвеса є те, що неможливо визначити різницю між прискоренням та гравітаційним полем. У певний час під час поїздки Бетті вона відчуває себе притиснутою до свого місця, і вона інтерпретує це як доказ того, що вона знаходиться в космічному судні, яке зазнає жорстоких прискорень і уповільнень. Але однаково можливо, що Tutorbot просто влаштував, щоб її капсула була підвішена до мотузки і бовталася в гравітаційне поле планети. Припустимо, що перше пояснення правильне. Капсула спочатку знаходиться в стані спокою в космічному просторі, де немає сили тяжіння. Бетті може випустити олівець і свинцеву кульку в повітря всередині салону, і вони залишаться на місці. Потім капсула прискорюється, і Бетті, яка прийняла рамку відліку, прив'язану до її палубі, стелі та стін, здається, що олівець і м'яч падають на палубу. Вони гарантовано залишатимуться пліч-о-пліч, поки не вдарять про палуби, тому що насправді вони не прискорюються; вони просто, здається, прискорюються, коли насправді це колоди, які піднімаються і вражають їх. Але тепер розглянемо друге пояснення, що капсула була занурена в гравітаційне поле. Куля і олівець все одно будуть падати пліч-о-пліч на підлогу, тому що мають однакове відношення гравітаційної до інерційної маси.

Принцип еквівалентності

Це призводить до одного способу встановлення центрального принципу відносності, відомого як принцип еквівалентності: Прискорення та гравітаційні поля еквівалентні. Не існує експерименту, який би міг відрізнити одне від іншого. ¹⁶

Примітка

Це твердження принципу еквівалентності узагальнено разом з деякими іншими його формами, з якими слід зіткнутися пізніше.

Щоб побачити, що це за радикальний відхід, нам потрібно порівняти з абсолютно іншою картиною, представленої ньютонівською фізикою і особливою відносністю. Закон інерції Ньютона стверджує, що «Кожен об'єкт зберігається у своєму стані спокою або рівномірного руху по прямій лінії, якщо тільки він не змушений змінити цей стан силами, враженими на нього». ¹⁷ Намір Ньютона тут полягав у тому, щоб чітко констатувати протиріччя Аристотелевської фізики, в якій предмети повинні були природним чином перестати рухатися і прийти в спокій за відсутності сили. Для Аристотеля «в спокої» означало спокій щодо Землі, що представляло собою особливу рамку відліку. Але якщо рух природно не зупиняється за власним бажанням, то більше немає ніякого способу виділити одну систему відліку, наприклад, прив'язану до Землі, як особливу. Не менш хорошою системою відліку є автомобіль, що рухається по прямій лінії вниз по міждержавній з постійною швидкістю. Земля і автомобіль обидва представляють дійсні інерційні системи відліку, в яких діє закон інерції Ньютона. З іншого боку, існують і інші, неінерційні системи відліку, в яких порушується закон інерції. Наприклад, якщо автомобіль раптово сповільнюється, то людям у машині здається, що їхні тіла смикаються вперед, хоча немає фізичного об'єкта, який міг би чинити на них будь-яку силу вперед. Ця відмінність між інерційними та неінерційними рамками відліку було перенесено Ейнштейном у його теорію спеціальної відносності, опубліковану в 1905 році.

Примітка

перефразовано з перекладу Мотта, 1729

Але до того часу, коли він опублікував загальну теорію в 1915 році, Ейнштейн зрозумів, що ця відмінність між інерційною та неінерційною системами відліку є принципово підозрілою. Як ми знаємо, що конкретна система відліку є інерційною? Одним із способів є перевірка того, що його рух відносно якоїсь іншої інерційної рамки, наприклад Землі, знаходиться по прямій лінії і з постійною швидкістю. Але як все це починається? Нам потрібно завантажувати процес принаймні з одним кадром відліку, щоб діяти як наш стандарт. Ми можемо шукати кадр, в якому діє закон інерції, але тепер стикаємося з іншою складністю. Щоб переконатися, що закон інерції дотримується, ми повинні перевірити, чи спостерігач, прив'язаний до цього кадру, не бачить об'єктів, що прискорюються без причини. Біда тут полягає в тому, що за принципом еквівалентності немає можливості визначити, прискорюється чи об'єкт «без причини» або через силу гравітаційної сили. Бетті, наприклад, не може сказати будь-яким місцевим вимірюванням (тобто будь-яким вимірюванням, що проводиться всередині капсули), чи знаходиться вона в інерційній або неінерційній рамці.

Малюнок\(\PageIndex{6}\): Чи не було б приємно, якби ми могли визначити значення ньютонівської інерційної системи відліку? Ньютон дозволяє звучати легко: щоб визначити інерційний кадр, просто знайдіть якийсь об'єкт, який не прискорюється, оскільки на нього не діють ніякі зовнішні сили. Але який об'єкт ми використали б? Земля? «Фіксовані зірки?» Наша галактика? Наше суперскупчення галактик? Все це прискорюється — відносно чогось.

Ми могли б сподіватися вирішити неоднозначність, зробивши замість цього нелокальні вимірювання. Наприклад, якби Бетті дозволили подивитися ілюмінатор, вона могла б спробувати сказати, чи прискорюється її капсула щодо зірок. Навіть ця можливість закінчується не задовільною. Зірки в нашій галактиці рухаються по кругових орбітах навколо галактики. У ще більших масштабах Всесвіт розширюється після Великого вибуху. Він провів близько першої половини своєї історії сповільнюючись через гравітаційне тяжіння, але зараз спостерігається розширення, що прискорюється, мабуть, через погано вивчене явище, яке називається загальним терміном «темна енергія». Загалом, у Всесвіті немає віддаленого фону фізичних об'єктів, який не прискорюється.

Лоренц Рамки

Висновок полягає в тому, що потрібно відмовитися від всієї відмінності між інерційними та неінерційними рамками відліку в стилі Ньютона. Найкраще, що ми можемо зробити, це виділити певні рамки відліку, визначені рухом об'єктів, які не піддаються будь-яким негравітаційним силам. Падаюча скеля визначає таку систему відліку. У цьому каркасі скеля знаходиться в стані спокою, а грунт прискорюється. Світова лінія породи є прямою лінією постійної x = 0 і змінною t. Така вільно падаюча система відліку називається рамкою Лоренца. Рамка відліку, визначена скелею, що сидить на столі, є інерційною системою відліку відповідно до ньютонівського погляду, але це не кадр Лоренца.

У ньютонівській фізиці краще інерційні кадри, оскільки вони роблять рух простим: об'єкти, які не діють на них сил, рухаються по прямих світових лініях. Аналогічно, кадри Лоренца займають привілейоване становище в загальній теорії відносності, оскільки вони роблять рух простим: об'єкти рухаються по «прямих» лініях світу, якщо у них немає негравітаційних сил, що діють на них.

Приклад 1: Штучний горизонт

Пілот літака не завжди може легко сказати, який шлях вгору. Горизонт може бути не рівним просто тому, що земля має фактичний нахил, і в будь-якому випадку горизонт може бути не видно, якщо погода туманна. Можна уявити, що проблему можна вирішити просто повісивши маятник і спостерігаючи, в який бік він вказував, але за принципом еквівалентності маятник не може визначити різницю між гравітаційним полем і прискоренням літака відносно землі - як і будь-який інший акселерометр, такі як внутрішнє вухо пілота.

Малюнок\(\PageIndex{7}\)

Наприклад, коли літак повернеться вправо, акселерометри будуть обманом вважати, що «вниз» вниз і вліво. Щоб обійти цю проблему, літаки використовують пристрій під назвою штучний горизонт, який по суті є гіроскопом. Гіроскоп повинен бути ініціалізований, коли площина, як відомо, орієнтована в горизонтальній площині. Жоден гіроскоп не ідеальний, тому з часом він буде дрейфувати. З цієї причини прилад також містить акселерометр, а гіроскоп автоматично відновлюється відповідно до узгодження з акселерометром, з постійною часом в кілька хвилин. Якщо літак пролітає колами протягом декількох хвилин, штучний горизонт буде обдурений, вказуючи на те, що неправильне напрямок вертикальне.

Приклад 2: немає антигравітації

Весь цей ланцюжок міркувань був заснований на нульових результатах експериментів Eötvös. У мультфільмах Rocky та Bullwinkle є не-етвезіанська речовина під назвою upsidasium, яка падає вгору, а не вниз. Його відношення гравітаційної до інерційної маси, мабуть, негативне. Якби таку речовину можна було б знайти, це сфальсифікувало б принцип еквівалентності. Приклад 10.

Малюнок\(\PageIndex{8}\): Бари upsidasium зберігаються на спеціальних складах, прикручених до землі. © Jay Ward Productions, що використовується відповідно до США сумлінного використання виняток із закону про авторське право.

Оперативне визначення кадру Лоренца

Ми можемо визначити кадр Лоренца в оперативному плані, використовуючи ідеалізовану варіацію (рис.\(\PageIndex{9}\)) на пристрої, фактично побудованому Гарольдом Уейдж у Прінстоні, як демонстрацію лекції, яку використовує його партнер у злочині Джон Уілер. Побудуйте герметичну камеру, вміст якої ізольовано від усіх негравітаційних сил. З чотирьох відомих сил природи три, які нам потрібно виключити, - це сильна ядерна сила, слабка ядерна сила та електромагнітна сила. Сильна ядерна сила має діапазон лише близько 1 фм (10 ⁻¹⁵ м), тому, щоб виключити її, нам просто потрібно зробити камеру товстішою, ніж ця, а також оточити її достатньою кількістю парафіну, щоб уникнути будь-яких нейтронів, які трапляються пролітають повз. Слабка ядерна сила також має невелику дальність дії, і хоча екранування від нейтрино - практична неможливість, їх вплив на апарат всередині буде незначним. Для захисту від електромагнітних сил оточуємо камеру кліткою Фарадея і суцільним листом му-металу. Нарешті, ми стежимо за тим, щоб камера не торкалася жодної навколишньої речовини, щоб виключити залишкові електричні сили короткого діапазону (липкі сили, хімічні зв'язки тощо). Тобто, камеру не можна підтримувати, вона вільно падає.

Малюнок\(\PageIndex{9}\): Сферична камера, показана на вирізаному вигляді, має шари екранування для виключення всіх відомих негравітаційних сил. Після того, як камера була відкалібрована шляхом маркування трьох траєкторій штрихової лінії в умовах вільного падіння, спостерігач всередині камери завжди може сказати, чи знаходиться вона в кадрі Лоренца.

Що найважливіше, екранування не виключає гравітаційних сил. Насправді не існує відомого способу захисту від гравітаційних ефектів, таких як залучення інших мас або поширення гравітаційних хвиль. Оскільки екранування сферичне, воно не надає власної гравітаційної сили на апарат всередині.

Усередині спостерігач проводить початкову калібрування, стріляючи кулями вздовж трьох декартових осей та простежуючи їх шляхи, які вона визначає як лінійні.

Ми пішли на складні довжини, щоб показати, що ми дійсно можемо визначити, без прив'язки до будь-якої зовнішньої системи відліку, що на камеру не діють будь-які негравітаційні сили, так що ми знаємо, що вона вільно падає. Крім того, ми також хочемо, щоб спостерігач міг сказати, чи обертається камера. Вона могла б дивитися через ілюмінатор на зірки, але в цьому не вистачало б всієї точки, яка полягає в тому, щоб показати, що без посилання на будь-який інший об'єкт ми можемо визначити, чи є конкретний кадр кадром Лоренца. Одним із способів зробити це було б спостерігати за прецесією гіроскопа. Або, не вдаючись до додаткового апарату, спостерігач може перевірити, чи змінюються шляхи, простежені кулями, коли вона змінює дульну швидкість. Якщо вони це роблять, то вона робить висновок, що є залежні від швидкості сили Коріоліса, тому вона повинна обертатися. Потім вона може використовувати маховики, щоб позбутися від обертання, і повторити калібрування.

Після початкового калібрування вона завжди може сказати, чи знаходиться вона в кадрі Лоренца чи ні. Вона просто повинна стріляти кулями, і подивитися, чи йдуть вони за попередньо відкаліброваними шляхами. Наприклад, вона може виявити, що рама стала не-лоренціанской, якщо камера обертається, дозволяється спиратися на землю, або прискорюється ракетним двигуном.

Може здатися, що детальна побудова цього складного мислення-експерименту не робить нічого іншого, як підтверджує щось очевидне. Тоді варто зазначити, що ми насправді не знаємо, працює це чи ні. Він працює в загальній теорії відносності, але є й інші теорії гравітації, такі як гравітація Бренса-Діка, які також узгоджуються з усіма відомими спостереженнями, але в яких апарат на малюнку 1.5.8 не працює. Два припущення, зроблені вище, зазнають невдачі в цій теорії: існують ефекти гравітаційного екранування, і ефекти Коріоліса стають непомітними, якщо поблизу недостатньо іншої речовини.

Місцевість кадрів Лоренца

Було б зручно, якби ми могли визначити єдиний кадр Лоренца, який би охопив весь всесвіт, але ми не можемо: на малюнку 1.5.9 дві дівчини одночасно падають з гілок дерев — одна в Лос-Анджелесі та одна в Мумбаї. Дівчина вільно падаюча в Лос-Анджелесі визначає кадр Лоренца, і в цьому кадрі інші об'єкти, що падають поруч, також матимуть прямі світові лінії. Але в системі відліку дівчини Лос-Анджелеса дівчина, що падає в Мумбаї, не має прямої світової лінії: вона прискорюється до дівчини Лос-Анджелеса з прискоренням близько 2 г.

Малюнок\(\PageIndex{10}\): Дві локальні кадри Лоренца.

Другий спосіб встановлення принципу еквівалентності полягає в тому, що завжди можна визначити локальний кадр Лоренца в певному районі простору-часу. ¹⁸ Неможливо зробити це на універсальній основі.

Примітка

Це твердження принципу еквівалентності узагальнено разом з деякими іншими його формами в додатку С.

Місцевість кадрів Лоренца можна зрозуміти за аналогією струни, розтягнутої по всій земній кулі. Ми не помічаємо кривизни земної поверхні в повсякденному житті, оскільки радіус кривизни становить тисячі кілометрів. На карті Лос-Анджелеса ми не помічаємо жодної кривизни, а також не виявляємо її на карті Мумбаї, але неможливо зробити плоску карту, яка включає як Лос-Анджелес, так і Мумбаї, не побачивши серйозних спотворень.

Термінологія

Значення слів еволюціонують з часом, і оскільки відносність зараз століття, в її номенклатурі відбувся певний заплутаний смисловий дрейф. Це стосується як «інерційного кадру», так і до «особливої відносності».

Ранні формулювання загальної відносності ніколи не стосуються «інерційних кадрів», «кадрів Лоренца» або чогось іншого цього аромату. Найпершою темою в оригінальному систематичному викладі Ейнштейна теорії ¹⁹ є приклад (рис. 1.5.10), що включає дві планети, метою яких є переконати читача в тому, що всі системи відліку створені рівними, і що будь-яка спроба зробити деякі з них в другу- класові громадяни підступні. Інші методи лікування загальної відносності з тієї ж епохи слідують лідерству Ейнштейна. ²⁰ Біда в тому, що цей приклад є скоріше твердженням прагнень Ейнштейна до його теорії, ніж точним зображенням фізики, яку він насправді передбачає. Загальна відносність дійсно дозволяє зробити однозначну різницю між кадрами Лоренца і не-Лоренца кадрів, як описано раніше. Заява Ейнштейна повинна була бути слабшою: закони фізики (наприклад, рівняння поля Ейнштейна) однакові у всіх рамках (Лоренц або не-Лоренц). Цим відрізняється ситуація в ньютонівській механіці і особливої теорії відносності, де закони фізики приймають найпростішу форму тільки в ньютон-інерційних рамках.

Малюнок\(\PageIndex{11}\) - Одна планета обертається навколо своєї осі, а інша - ні. Як обговорювалося більш детально пізніше, Ейнштейн вважав, що загальна відносність була ще більш радикально егалітарною щодо систем відліку, ніж вона є насправді. Він думав, що якби планети були одні в іншому порожньому всесвіті, не було б можливості сказати, яка планета насправді обертається, а яка ні, так що екваторіальна опуклість Б повинна зникнути. Не було б ніякого способу сказати, на якій поверхні планети був кадром Лоренца.

Примітка

Два, які, на мою думку, були відносно впливовими, - це теорія відносності Ейнштейна 1920 року і Еддінгтона 1924 Математична теорія відносності. Народжений слідкує за папером «Фонд» Ейнштейна рабським. Еддінгтон, здається, лише згадує інерційні кадри в декількох місцях, де контекст є ньютонівським.

Оскільки Ейнштейн не хотів робити відмінності між кадрами, ми опинилися осідлані незручною для них термінологією. Найменш словесно незручний вибір - викрасти термін «інерційний», переосмисливши його з його ньютонівського значення. Тоді ми говоримо, що поверхня Землі не є інерційною рамкою, в контексті загальної відносності, тоді як в ньютонівському контексті це інерційний кадр до дуже хорошого наближення. Це використання досить стандартне, ²¹, але зробило б Ньютона заплутаним, а Ейнштейна нещасним. Якщо ми дотримуємось цього використання, то нам іноді доведеться сказати «Ньютоніанінерційний» або «Ейнштейн-інерційний». Більш незручним, але також більш точним терміном є «кадр Лоренца», як використовується в цій книзі; це, здається, широко розуміється. ²²

Різниця між особливою та загальною відносністю зазнала подібного зрушення протягом десятиліть. Ейнштейн спочатку визначив відмінність з точки зору допустимості прискореної системи відліку. Це, однак, ставить нас у абсурдну позицію сказати, що спеціальна відносність, яка, як передбачається, є узагальненням ньютонівської механіки, не може обробляти прискорені системи відліку так само, як це може ньютонівська механіка. Насправді і ньютонівська механіка, і спеціальна теорія відносності ставляться до ньютонівських неінерційних систем відліку однаково: змінюючи закони фізики, щоб вони не набули своєї найпростішої форми (наприклад, порушуючи третій закон Ньютона), зберігаючи при цьому можливість змінювати координати назад до бажаного рамки, в яких застосовуються більш прості закони. Досить рано ²³ було усвідомлено, що важлива відмінність полягала між особливою відносністю як теорією плоского простору-часу та загальною теорією відносності як теорією, яка описувала гравітацію з точки зору вигнутого простору-часу. Всі релятивісти, що пишуть приблизно з 1950 року, здається, погоджуються з цим більш сучасним переосмисленням термінів. ²⁴

У прискорювальному кадрі принцип еквівалентності говорить нам, що вимірювання вийдуть такими ж, як якщо б було гравітаційне поле. Але якщо просторовий час плоский, опис його в прискорювальному кадрі не робить його вигнутим. (Кривизна є фізичною властивістю простору-часу, і її неможливо змінити з нуля на ненульове просто за допомогою вибору координат.) Таким чином, відносність дозволяє нам мати гравітаційні поля в плоскому просторі - але лише для певних спеціальних конфігурацій, таких як ця. Спеціальна відносність здатна працювати просто чудово в цьому контексті. Наприклад, Чунг та ін. ²⁵ зробив високоточний тест спеціальної відносності в 2009 році, використовуючи інтерферометр матерії у вертикальній площині, спеціально для того, щоб перевірити, чи не було порушення спеціальної відносності в рівномірному гравітаційному полі. Їх експеримент трактується чисто як тест особливої відносності, а не загальної відносності.

Парадокс Чіао

Решта цього підрозділу стосується тонкого питання про те, чи можна застосувати принцип еквівалентності до заряджених частинок. Можливо, ви захочете пропустити його при першому читанні. Коротка відповідь полягає в тому, що використання принципу еквівалентності, щоб зробити висновки про заряджені частинки, схоже на спроби рабів і аболіціоністів в США 19 століття підтримати свої позиції на основі Біблії: ви, ймовірно, можете довести, який би висновок був той, який ви мали намір довести.

Малюнок\(\PageIndex{12}\) - Парадокс Чіао: заряджена частинка і нейтральна частка знаходяться на орбіті навколо Землі. Чи буде заряджена частинка випромінювати, порушуючи принцип еквівалентності?

Принцип еквівалентності не є єдиним, простим, математично чітко визначеним твердженням. ²⁶ Як приклад неоднозначності, яка все ще є дещо суперечливою, через 90 років після того, як Ейнштейн вперше запропонував принцип, розглянемо питання про те, чи застосовується він до заряджених частинок. Раймонд Чіао ²⁷ пропонує наступний експеримент з думкою, який я буду називати парадокс Чіао. Нехай нейтральна частинка і заряджена частинка будуть встановлені поруч на орбіті навколо Землі. Припустимо (нереально), що простір навколо землі не має електричного або магнітного поля. Якщо принцип еквівалентності застосовується незалежно від заряду, то ці дві частинки повинні йти на орбіту дружно, пліч-о-пліч. Але тоді ми маємо порушення збереження енергії, так як заряджена частинка, яка прискорюється, буде випромінювати електромагнітні хвилі (з дуже низькою частотою і амплітудою). Здається, що орбіта частинки повинна розпастися.

Примітка

Хорошим недавнім обговоренням цього є «Теорія теорій гравітації: звіт про відсутність прогресу», Сотіріу, Фараоні та Лібераті, http://arxiv.org/abs/0707.2748

Дозвіл парадоксу, як продемонстрували волохаті розрахунки ²⁸, цікавий тим, що він ілюструє локальний характер принципу еквівалентності. Коли заряджена частинка рухається через гравітаційне поле, в цілому частинка може відчувати реакцію від власних електромагнітних полів. Це може здатися неможливим, оскільки спостерігач у кадрі на мить перебуває у спокої щодо частинки бачить, як випромінювання злітає у всі боки зі швидкістю світла. Але насправді існує кілька різних механізмів, за допомогою яких заряджена частинка може возз'єднатися зі своїм давно втраченим електромагнітним потомством. Приклад (не пов'язаний безпосередньо зі сценарієм Чіао) наступний.

Примітка

Перший детальний розрахунок, здається, був Сесіль та Брайс ДеВітт, «Падіння зарядів», Фізика 1 (1964) 3. Цей документ, на жаль, дуже важко отримати зараз. Більш недавнє лікування Греном і Нессом доступне за адресою arxiv.org/abs/0806.0464v1. Повну експозицію технік дає Пуассон, «Рух точкових частинок у криволінійному просторовому часі», www.livingreviews.org/lrr-2004-6.

Піднесіть лазер дуже близько до чорної діри, але не настільки близько, щоб він збився всередині горизонту подій, який є сферичною точкою неповернення зсередини, з якої ніщо не може втекти. Приклад 14 дає аргумент правдоподібності на основі ньютонівської фізики, що радіус ²⁹ горизонту подій повинен бути чимось на зразок\(r_{H} = \frac{GM}{c^{2}}\), а розділ 6.3 виводить відносно правильний коефіцієнт 2 попереду, так що\(r_{H} = \frac{2GM}{c^{2}}\). Виходить, що при r =\(\left( \frac{3}{2}\right) r_{H}\) промінь світла може мати кругову орбіту навколо чорної діри. Оскільки це більше r _H, ми можемо, принаймні теоретично, утримувати лазер нерухомим при цьому значенні r за допомогою потужного ракетного двигуна. Якщо навести лазер в азимутальному напрямку, його власний промінь повернеться назад і вдарить по ньому.

Примітка

Оскільки відносність описує гравітаційні поля з точки зору кривизни просторучасу, евклідова залежність між радіусом та окружністю кола тут не вдається. Координату r слід розуміти тут не як радіус, виміряний від центру, а як окружність, поділену на 2\(\pi\).

Оскільки матерія може відчувати зворотну реакцію від власного електромагнітного випромінювання, стає правдоподібним, як можна вирішити парадокс. Принцип еквівалентності тримається локально, тобто в межах невеликої ділянки простору і часу. Якщо заряджена та нейтральна частинка Чіао випущені пліч-о-пліч, то вони будуть підкорятися принципу еквівалентності принаймні певну кількість часу - і «принаймні певну кількість часу» - це все, що ми повинні очікувати, оскільки принцип локальний. Але через деякий час заряджена частинка почне відчувати зворотну реакцію від власних електромагнітних полів, і це призводить до розпаду її орбіти, задовольняючи збереження енергії. Оскільки частинки Чіао обертаються навколо землі, а земля не є чорною дірою, механізм явно не може бути таким простим, як описаний вище, але Грён і Несс показують, що існують подібні механізми, які можуть застосовуватися тут, наприклад, розсіювання світлових хвиль неоднорідним гравітаційним полем.

Варто мати на увазі застереження Девітта, що «Питання, на які відповідає це дослідження, представляють лише концептуальний інтерес, оскільки залучені сили занадто малі, щоб їх можна було виявити експериментально» (див. Задача 8).

Посилання

^{Брагінський В.Б.і Панов В.І., Радянська фізика JETP 34, 463 (1972).}

¹⁴ Carusotto et al., «Обмеження на порушення g-універсальності з експериментом Галілеотипу», Phys Lett A183 (1993) 355. Вільно доступний в Інтернеті за адресою researchgate.net.

¹⁵ Touboul et al., «Місія МІКРОСКОПА: перші результати космічного випробування принципу еквівалентності», arxiv.org/abs/1712.01176

¹⁹ Ейнштейн, «Основа загальної теорії відносності», 1916. Витяг дається пізніше.

²¹ Міснер, Торн і Уілер, Гравітація, 1973, стор. 18

²² там же, с. 19

²³ Еддінгтон, оп. місто.

²⁴ Міснер, Торн, і Уілер, op. cit. , С.163-164. Пенроуз, Дорога до реальності, 2004, стор. 422. Тейлор і Уілер, Фізика космічного часу, 1992, стор. 132. Шуц, Перший курс загальної теорії відносності, 2009, стор. 3, 141. Хобсон, Загальна відносність: Вступ для фізиків, 2005, сек. 1.14.

²⁵ arxiv.org/абс/09.05.1929

²⁷ arxiv.org/абс/квант-ф/0601193v7