3.9: Потовщення кривої

Цілі навчання

• Інтерпретувати прискорення геометрично

Геометрична інтерпретація прискорення

Ми інтерпретували вектор прискорення як міру кривизни світової лінії, але щоб зробити це більше, ніж інструмент для візуалізації, нам доведеться визначити, що ми маємо на увазі під кривизною. Хороший спосіб підійти до цього показаний на малюнку$\PageIndex{1}$ (1).

Малюнок$\PageIndex{1}$: Односторонні потовщення кола і відрізка лінії.

Тут коло окружності$L$ було розширено, як буханець піднімається хліба, до кола більшої окружності$L∗$. Це збільшення відбувається тільки тому, що коло вигнутий. Якщо ми зробимо те ж саме з відрізком лінії, фігурою$\PageIndex{1}$ (2), збільшення довжини немає. Збільшення довжини говорить нам про кривизну.

Кількісно припустимо, що товщина затіненої області дорівнює$∆h$. Тоді збільшення окружності$∆L = L∗ - L$ задається

$$\frac{1}{L}\frac{\Delta L}{\Delta h} = k$$

де$k$ - міра кривизни, а$k = 1/r$ для кола. Ми можемо сприймати це як визначення кривизни кривої, вбудованої в двовимірну евклідову площину. Криві на малюнку$\PageIndex{1}$ (1) мають постійну кривизну, і якби ми застосували своє визначення до будь-якого короткого відрізку з них, ми б отримали ту саму відповідь. Для кривої з різною кривизною, наприклад букви «»$S$, кривизну можна визначити як відповідну межу в будь-якій заданій точці, оскільки довжина відрізка, що охоплює точку, наближається до нуля. Зауважте, що нам довелося вибрати орієнтацію для розширення, тобто напрямок, в якому потрібно розширюватися. З огляду на таку спрямованість, має сенс говорити про підписаних значеннях$h$ і$k$. Якщо ми вибираємо зовнішню орієнтацію для кола, то$k$ вона позитивна.

Цікавим моментом цього визначення є те, що воно є зовнішнім, а не внутрішнім, у сенсі, визначеному в розділі 2.2. Тобто це залежить від того, як крива вбудована в навколишній двовимірний простір, і це залежить від евклідової метрики цього простору. Оскільки крива - це одновимірний об'єкт, немає нічого внутрішнього для кривої, що дозволило б нам визначити її кривизну. Уявіть себе крихітним жуком - настільки крихітним, що ви точкові. Якщо крива представляє ваш Всесвіт, то ви можете досліджувати її скільки завгодно, але ви ніколи не зможете виявити ніяких внутрішніх доказів її кривизни. Це не так у двох вимірах. Наприклад, клоп, що живе на двовимірній поверхні сфери, може виявити її кривизну, малюючи трикутники і вимірюючи, наскільки сума їх внутрішніх кутів відрізняється від$180$ градусів. Це було б внутрішньою мірою кривизни.

Визначення, наведене вище, легко поширюється від евклідового простору до$1 + 1$ розмірів простору-часу. $\PageIndex{2}$На малюнку показано одностороннє потовщення прискореної світової лінії.

Малюнок$\PageIndex{2}$: Одностороннє потовщення світової лінії.

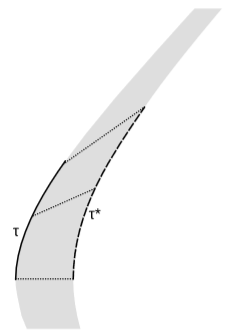
Хоча затінена область не виглядає рівномірно товстою для наших евклідових очей, це так. Наприклад, кожна з пунктирних ліній ортогональна до початкової світової лінії зліва, і всі вони мають таку ж довжину,$∆h$ як вимірюється спостерігачем, який простежує цю світову лінію. Тобто кожна з цих ліній може представляти собою жорсткий вимірювальний стрижень, проведений цим спостерігачем, проведений вздовж лінії, яку цей спостерігач вважає лінією одночасності в той час. За аналогією з евклідовим випадком ми маємо

$$\frac{1}{\tau }\frac{\Delta \tau }{\Delta h} = \frac{1}{a}$$

Парадокс космічного корабля Белла

Варіація ситуації, показаної на малюнку,$\PageIndex{2}$ призводить до парадоксу з філософськими наслідками, запропонованим Джоном Белом. Белл обійшов кафетерію ЦЕРН, запропонувавши фізикам обідати наступний експеримент з думками, і він виявив, що майже всі вони помилилися.

Малюнок$\PageIndex{3}$: Парадокс космічного корабля Белла.

Нехай два космічних корабля прискорюються, як показано на малюнку$\PageIndex{3}$. Кожен корабель оснащений двором-плечем, а між двома руками зав'язується нитка, фігура$\PageIndex{3}$ (1). Неприскорений спостерігач$o$ використовує координати Мінковського$(t,x)$, як показано на малюнку$\PageIndex{3}$ (2). Прискорення, як судять по$o$, рівні для двох кораблів як функції$t$. Чи розривається нитка через стиснення Лоренца?

Принципова відмінність між фігурами$\PageIndex{2}$ і$\PageIndex{3}$ (2) полягає в тому, що в першому потовщення світової лінії здійснювалося уздовж пунктирних нормалей, тоді як друга світова лінія - це просто копія першої, яка була зрушена вправо, паралельно$x$ -осі.

Популярна відповідь у кафетерії ЦЕРН полягала в тому, що нитка не зламається, міркуючи, що скорочення Лоренца є залежним від кадру ефектом, і такого скорочення не спостерігалося б в рамах ракет.

Помилка в цих міркуваннях полягає в тому, що прискорення двох кораблів були вказані рівними за рамкою$o$, а не в рамах ракет. Координати Мінковського,$(t',x')$ показані на малюнку$\PageIndex{3}$ (2), відповідають кадру інерційного спостерігача$o'$, який на мить рухається разом із задньою ракетою після того, як прискорення триває деякий час. $x'$Вісь є лінією одночасності для$o'$, і ця вісь перетинає провідну світову лінію корабля в точці, яка$o$ вважає пізніше в часі. Тому$o'$ говорить про те, що провідний корабель досяг більшої швидкості, ніж задній. У$o'$, два кораблі' прискорення нерівні.

Ми також можемо бачити безпосередньо з діаграми простору/часу, що тоді як довжина$L_1$ - це$4$ одиниці виміру спостерігача спочатку в спокої відносно потоку,$L_2$ це приблизно$5$ одиниці виміру$o'$, який знаходиться в спокої відносно кінцевого кінця нитки в більш пізній час. . Так$L_2$ як більше ненаголошеної довжини$L_1$, нитка знаходиться під натягом.

Малюнок$\PageIndex{3}$ (3) більше відповідає духу аналізу Белла. У каркасі$o$ нитка має початкову, ненаголошену довжину$L$. Якби нитка була прикріплена тільки до провідного корабля, то вона б причепилася за нею, ненаголошеною, зі скороченою довжиною Лоренца$L/γ$. Оскільки його фактична довжина відповідно до o все ще$L$, вона була розтягнута щодо ненаголошеної довжини.

Цей парадокс стосується складного філософського питання про те, чи є «реальними» розширення часу та скорочення довжини, передбачені відносністю. Це залежить, звичайно, від того, що мається на увазі під «реальним». Вони залежні від кадрів, тобто спостерігачі в різних системах відліку не погоджуються з ними. Але це мало говорить нам про їхню реальність, оскільки швидкості залежать від кадру в ньютонівській механіці, але ніхто не турбується про те, чи реальні швидкості. Белл сприйняв неправильні відповіді своїх колег як доказ того, що їх інтуїція була помилкова стандартним способом наближення до цього питання про реальність скорочень Лоренца.

Ця обробка має одну бородавку на ньому, яка полягає в тому, що ми судили відстань між двома кораблями в системі відліку, миттєво рухаючись з заднім кораблем, але це трохи відрізняється від довжини, визначеної в кадрі провідного корабля. Один із способів видалення цієї бородавки - відзначити, що дробове розбіжність$∆L_1/L_1$ є порядком$v^3$, яке має менший порядок, ніж деформація в нитці, яка є порядковою$v^2$. Однак суворо проводити оцінку помилок такого типу було б громіздко. Більш елегантний і строгий підхід наведено в розділі 9.5, де ми використовуємо більш химерні прийоми, щоб показати, що рух, показаний на малюнку,$\PageIndex{2}$ є унікальним рухом, який дозволяє кожній частині струни рухатися без напруги.

Ця презентація включає ідеї, внесені користувачами форумів фізики tiny-tim і PeterDonis.

Дежавю, жамай-вю

Дежавю все знову

Малюнок$\PageIndex{4}$: Дежавю.

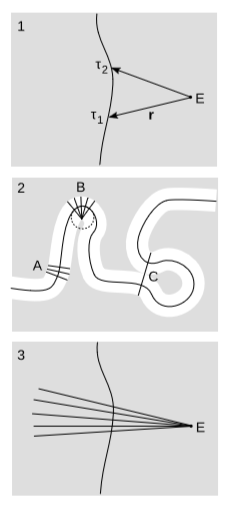
У прикладі 1.4.7 ми побачили, що коли спостерігач прискорюється, він може вважати подію одночасною з нею не раз. Тобто, враховуючи гладку, схожу на час світову лінію,$r(τ)$ параметризовану відповідним часом$E$, і подію, яку ми приймаємо як початок нашої системи координат, може бути більше одного часу, в якому$r$ ортогонально вектору швидкості$v$ (рисунок$\PageIndex{4}$ (1)). Як зазначалося раніше, це лише проблема із застосуванням певної довільної конвенції про маркування до певного прикладу, а не катастрофічної кризи у фізиці. Тим не менш, характеризувати обставини, за яких це може статися, становить певний внутрішній геометричний інтерес. Ми хотіли б розмістити якусь пов'язану з тим, скільки прискорення потрібно і наскільки віддаленим має бути Е.

Як розминки розглянемо аналогічну задачу в евклідовому просторі, малюнок$\PageIndex{4}$ (2). Тут ми маємо поняття трубчастої околиці, яка є найбільшим потовщенням кривої$W$ таким чином, що жодна точка в ній не лежить на двох різних нормалей. Трубчаста околиця має радіус$r$, який є максимально можливим радіусом несамопересічного шматка мотузки, центральна вісь якого збігається з$W$. Зазвичай, як і в регіоні$A$, мотузка не перетинається сама. Є дві якісно різні причини, за якими мотузка могла самоперетинатися. Один локальний: радіус кривизни$W$ занадто малий, як при$B$, де$W$ збігається з окружністю радіуса$r$. Інший є глобальним: дві точки, які знаходяться далеко один від одного, як вимірюється вздовж,$W$ можуть бути близько один до одного в навколишньому евклідовому просторі, як у точці$C$.

Якщо перенести ці ідеї в простір Мінковського, то локальний випадок, малюнок$\PageIndex{4}$ (3), легко проаналізувати за допомогою розроблених нами методик. Аналогом радіуса кривизни є зворотне належного прискорення, що говорить про те, що ми повинні мати можливість отримати межу по радіусу трубчастого сусідства в плані прискорення. Визначте$f(\tau ) = r\cdot v$. У заданій точці на$W$,$f$ мінус координата часу Мінковського, що спостерігач, чия світова лінія$W$ буде призначити, в цей момент, до$E$. Умова для типу самоперетину, про який ми обговорюємо, полягає в тому, що обидва$f$ і його похідні щодо належного часу$f'$ зникають в тій же точці$W$. Диференціюючи f за допомогою правила продукту, знаходимо$f' = v\cdot v + r\cdot a = 1 + r\cdot a$ (в$+---$ підписі), так що$r\cdot a = -1$.

Зараз ми використовуємо той факт, що обидва$a$ і$r$ є ортогональними до$W$ — перший як загальний кінематичний факт, а другий тому$f = 0$. Це означає, що вони лежать в площині перпендикулярно$W$. Геометрія цієї площини є евклідовою, тому ми можемо застосувати евклідову нерівність$|a \cdot r| \leq |a| |r|$, де смуги зліва позначають абсолютне значення, а ті, що знаходяться праворуч, величини векторів. Тому ми маємо$|a| |r| \geq 1$. Оскільки$r$ ортогональний до$W$, ми можемо інтерпретувати його як належну відстань між$E$ і$W$. Величина$a$ - це правильне прискорення. Перетворення в одиниці з$c \neq 1$, ми маємо точну межу форми$\text{(proper distance)(proper acceleration)}\geq c^2$. У звичайних одиниць$c$ велика кількість, тому в цьому сенсі$E$ повинні бути віддаленими, а прискорення великим. Це пояснює, чому ми ніколи не стикаємося з такою проблемою в нерелятивістській фізиці.

Цього ніколи не було зараз

Поки що ми охарактеризували обставини, за яких одночасність може не бути унікальною. Одночасність також може не існувати. Наприклад, у тому ж позначенні візьміть$W$ постійне прискорення руху, описане в прикладі 3.5.1, і нехай$E$ буде подією$(-1,0)$. Тоді це легко може бути показано, що$f(τ)$ завжди позитивно, тому спостерігач, що рухається уздовж, завжди$W$ буде вважати,$E$ щоб бути в своєму минулому, а не її майбутньому. Немає часу для неї такого, що вона вважає$E$ «зараз». Функція десь$f$ доходить до максимуму, але ніколи не перетинає нуль.

Завжди буде якесь сусідство,$W$ всередині якого ми захищені від неіснування одночасності. Щоб визначити радіус цього сусідства, розглянемо подію,$B$ яка лежить на кордоні сусідства, і визначаємо з$f$ точки зору,$B$ а не$E$. Тоді$f(τ) = 0$ для деяких$τ$, але$f$ не перетинає нуль, так що або$f \leq 0$ всюди, або$f \geq 0$ всюди. На місці де$f(τ) = 0$, у нас теж є$f'(τ) = 0$, а решта аналіз такий же, як і раніше. Тому радіус трубчастої окружності, визначений у цьому прикладі, визначає радіус, в межах якого одночасність має як існування, так і унікальність.

Малюнок$\PageIndex{5}$: Крайова точка$B$ дійсно особлива.

Тлумачення такої граничної точки$B$ трохи смішно. Рисунок$\PageIndex{5}$ повторює рух, описаний у прикладі 3.5.1. Для цього руху єдиною точкою$B$ є позначена$(0,0)$ в координатах Мінковського, що використовується в цій деривації. Чи дійсно є щось особливе в цій точці, або це просто випадкова точка, яку ми випадково обрали як походження нашої системи координат? Спостерігач, що рухається по цьому,$W$ не вважає, що будь-яка точка просторучасу, доступна їй, має якісь особливі властивості. Вона завжди прискорювалася і завжди буде, тому жодна подія, яку вона може спостерігати або вплинути, не можна відрізнити від інших подій, які вона могла спостерігати або вплинути таким же чином у будь-який раніше чи пізніше. Але ми можемо легко показати, що$B$ є особливим, даючи опис його без прив'язки до будь-яких координат. $W$Давайте причинно-наслідкове майбутнє буде сукупністю всіх подій, які лежать у майбутньому світловому конусі якоїсь події на$W$, і аналогічно для$W$ причинно-наслідкового минулого. Межами цих двох сетів є$W$ минулий і майбутній горизонти подій, і ці горизонти збігаються лише на одній події, яка є$B$. Це здається парадоксальним, але наш спостерігач не може ні спостерігати$B$, ні впливати, тому суперечності немає.