3.3: Поєднання швидкостей

Last updated

Oct 27, 2022
Save as PDF
- 3.2: Коефіцієнт розтягування - це доплерівський зсув
- 3.4: Жодна система відліку не рухається на c

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Поясніть, як додати швидкості релятивістично

У нерелятивістській фізиці швидкості додають відносного руху. Наприклад, якщо човен рухається щодо річки, а річка рухається щодо суші, то швидкість човна щодо суші виявляється шляхом векторного складання. Ця лінійна поведінка не може триматися релятивістично. Наприклад, якщо космічний корабель рухається відносно землі зі швидкістю $3/5$ (в одиницях з $c = 1$ ), і він запускає зонд зі швидкістю $3/5$ відносно себе, ми не можемо змусити зонд рухатися зі швидкістю $6/5$ відносно землі, оскільки це було б більше максимальної швидкість причинно-наслідкового результату, яка є $1$ . Щоб побачити, як додати швидкості релятивістично, розглянемо ефект проведення двох перетворень Лоренца один за одним, фігура $\PageIndex{1}$ .

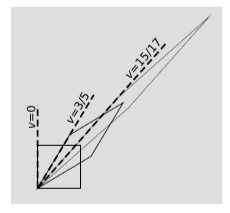
рис. 3.3.1.png — Малюнок $\PageIndex{1}$ : Два перетворення Лоренца $v = 3/5$ застосовуються один за одним. Перетворення представлені відповідно до графічних умовностей розділу 1.4.

Зворотний нахил лівої сторони кожного паралелограма вказує на його швидкість щодо вихідного кадру, представленого квадратом. Оскільки ліва сторона кінцевого паралелограма не прокотилася повз діагоналі, явно вона являє собою швидкість менше $1$ , не більше. Для визначення результату використовуємо той факт, що $D$ коефіцієнти множаться. Ми вибрали швидкості, $3/5$ тому що вона дає $D = 2$ , з якою легко працювати. Подвоєння довгою діагоналлю двічі дає загальний коефіцієнт розтягування $4$ , а рішення рівняння $D(v) = 4$ для $v$ дає результат $v = 15/17$ .

Тепер ми можемо побачити відповідь на питання 2 в розділі 3.0: Прелюдія до кінематики. Якщо ми продовжуємо неухильно прискорювати космічний корабель, ми просто продовжуємо процес прискорення, показаний на малюнку $\PageIndex{1}$ . Якщо ми зробимо це нескінченно, швидкість наблизиться, $c = 1$ але ніколи не перевершить її. (Докладніше про цю тему швидшого, ніж світло, див. Розділ 4.7.)

Приклад $\PageIndex{1}$ : Accelerating electrons

рис. 3.3.2.png — Малюнок $\PageIndex{2}$ : Прискорення електронів

$\PageIndex{2}$ На малюнку показані результати експерименту 1964 року Бертоцці, в якому електрони були прискорені статичним електричним полем $E$ прискорювача довжини Ван де Граафа $l_1$ . Потім їм було дозволено літати вниз по лінії променя довжини, $l_2 = 8.4$ $m$ не впливаючи на будь-яку силу. Час польоту $t_2$ використовувався для пошуку кінцевої швидкості, $v = \frac{l_2}{t_2}$ до якої вони були прискорені. (Щоб зробити низькоенергетичну частину графіка розбірливою, найвища точка енергетичних даних Бертоцці опущена.)

Якби ми вірили в закони Ньютона, то електрони мали б прискорення

$a_N = Ee/m$

яка була б постійною, якби, як ми прикидаємося на даний момент, поле $E$ було постійним. (Електричне поле всередині прискорювача Ван де Граафа насправді не зовсім рівномірне, але це виявиться не має значення.) Ньютонівське передбачення часу, за яке відбувається це прискорення, є

$t_N = \sqrt{2ml_1/eE}$

Прискорення, що $a_N$ діє протягом часу, $t_N$ повинно виробляти кінцеву швидкість

$a_Nt_N = \sqrt{2eV/m}$

де $V = El_1$ - різниця напруги. (За збереженням енергії це рівняння тримається, навіть якщо поле не є постійним.) Суцільна лінія на графіку показує прогноз законів Ньютона, який полягає в тому, що постійна сила, що постійно чиниться з часом, буде виробляти швидкість, яка піднімається лінійно і без обмежень.

Експериментальні дані, показані у вигляді чорних крапок, чітко розповідають іншу історію. Швидкість асимптотично наближається до межі, яку ми ідентифікуємо як $c$ . Пунктирна лінія показує прогнози особливої відносності, які ми ще не готові обчислити, оскільки ще не бачили, як кінетична енергія залежить від швидкості на релятивістських швидкостях.

Зверніть увагу, що зв'язок між першим і другим рамками відліку на малюнку $\PageIndex{1}$ така ж, як і зв'язок між другим і третім. Тому, якщо пасажир повинен відчувати стійке відчуття прискорення (або, що еквівалентно, якщо акселерометр на борту корабля повинен показувати постійне свідчення), то належний час, необхідний для проходження від першого кадру до другого, має бути таким же, як і належний час для переходу з другого на третій. Хороший спосіб висловити це - визначити швидкість$ η =\ ln D$. Поєднання швидкостей означає множення $D$ , що так само, як додавання їх логарифмів. Тому ми можемо написати релятивістське правило поєднання швидкостей просто так, як

$_ηc = η_1 + η_2$

Пасажири сприймають прискорення як стійке, якщо $η$ збільшитися на таку ж кількість за одиницю належного часу. Іншими словами, ми можемо визначити правильне прискорення $dη/dτ$ , яке відповідає тому, що вимірює акселерометр.

Швидкість зручна і корисна, і дуже часто використовується у фізиці частинок. Але в плані звичайних швидкостей правило поєднання швидкостей також можна переписати, використовуючи цю ідентичність з розділу 3.6 як

$v_c = \dfrac{v_1+v_2}{1+v_1v_2}. \label{eq3}$

Вправа $\PageIndex{1}$

Як ми можемо сказати, що Equation\ ref {eq3} записано в натуральних одиницях? Перепишіть його в одиниці СІ.