3.E: Кінематика (вправи)

Q1

Фред купує квиток на космічний корабель, який розганяється до ультрарелятивістської швидкості$v$ такої, що тільки$c - v$ є$6\: m/s$. Фред був у команді треку в середній школі, тому він знає, що може бігати$8\: m/s$. Як тільки корабель набере швидкість, Фред планує бігти в прямому напрямку, тим самим стаючи першою людиною, яка перевищила швидкість світла. Крім можливої відсутності гравітації, щоб дозволити біг, що не так з планом Фреда?

Q2

1. У рівнянні$v_c = \tfrac{v_1 +v_2}{1+v_1v_2}$ для поєднання швидкостей інтерпретуйте випадок, коли одна зі швидкостей (але не інша) дорівнює швидкості світла.
2. Тлумачити випадок, коли знаменник йде в нуль.
3. Скористайтеся геометричним рядом, щоб переписати множник\ [(tfrac {1} {1+v_1v_2}\), а потім розгорніть вираз у$v_c$ вигляді ряду в$v_1$ і$v_2$, зберігаючи терміни до третього порядку за швидкістю. Як це пов'язано з принципом листування?

Q3

Визначте, які з ідентичностей у розділі 3.6 потрібно змінити, щоб бути дійсними в одиницях з$c \neq 1$, і опишіть, як вони повинні бути змінені.

Q4

Великий адронний коллайдер прискорює протиобертові пучки протонів і стикається з ними лоб. Енергія променя поступово збільшувалася, а прискорювач розрахований на досягнення максимальної енергії$14\: TeV$, відповідної швидкості$10.3$.

1. Знайти швидкість променя.
2. При будь-якому зіткненні кінетична енергія, доступна для того, щоб зробити щось нееластичне (розбити ваш автомобіль, виробляти ядерні реакції,...) - це енергія в центрі маси кадру; в будь-якому іншому кадрі є початкова кінетична енергія, яка також повинна бути присутня в кінцевому стані завдяки збереженню імпульсу. Припустимо, що конкретний протон у пучку LHC ніколи не зазнає зіткнення з протоном з протилежного променя, а замість цього витрачається даремно, скидаючи в промінь. Скажімо, це зіткнення відбувається з протоном в атомі водню, залишеному чиїмось відбитком пальця. Знайдіть швидкості двох протонів у їхньому загальному центрі маси.

Q5

Кожен супутник GPS знаходиться на орбіті з радіусом$26,600\: km$, з орбітальним періодом в половину сидеричного дня, даючи йому швидкість$3.88\: km/s$. Атомний годинник на борту такого супутника налаштований на$10.22999999543\: MHz$, який обраний так, що коли супутник знаходиться безпосередньо над головою, ефект розширення часу (поперечний доплерівський зсув), в поєднанні з загально-релятивістським ефектом, обумовленим гравітацією, призводить до частоти точно$10.23\: MHz$. (GPS почався як військовий проект, і легенда свідчить, що верхня латунь, підозріла до божевільних речей відносності, вимагала, щоб супутники були оснащені програмним перемикачем, щоб вимкнути виправлення, на всякий випадок фізики помилялися.) Існують коливання, що накладаються на ці статичні ефекти внаслідок поздовжніх доплерівських зрушень, коли супутники наближаються і відступають від даного спостерігача на землі.

1. Обчисліть максимальну частоту зсуву доплера для гіпотетичного спостерігача в космічному просторі, до якого безпосередньо наближається супутник по його орбіті.
2. Насправді найбільша можлива поздовжня складова швидкості значно менша, ніж це завдяки геометрії. Використовуйте розмір землі для визначення цієї швидкості і відповідну максимальну частоту.

Q6

Переконайтеся безпосередньо, використовуючи геометрію малюнка нижче, що для$v = 3/5$, коефіцієнт доплерівського зсуву є$D = 2$. (Не просто підключіть$v = 3/5$ до формули$D =\sqrt{\frac{1 + v}{1-v}}$.)

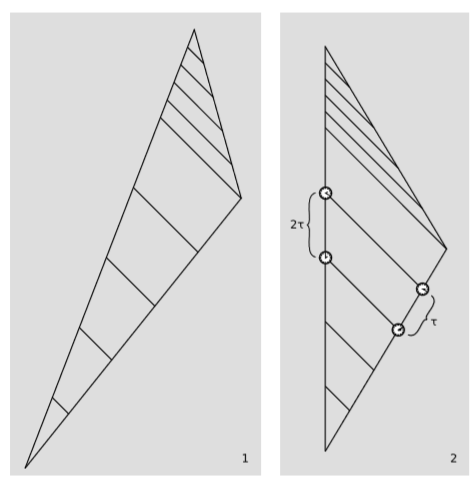
Q7

Узагальнити числовий розрахунок задачі Q6 для підтвердження загального результату$D =\sqrt{\frac{1 + v}{1-v}}$.

Q8

Розгорніть релятивістське рівняння для поздовжнього доплерівського зсуву світла$D(v)$ в ряді Тейлора та знайдіть перші два незникаючі члени. Покажіть, що ці два терміни погоджуються з нерелятивістським виразом, так що будь-який релятивістський ефект має вищий порядок в$v$.

Q9

Доведіть, як стверджується в розділі 3.5, що ми повинні мати,$a \cdot v = 0$ якщо швидкість чотири вектора залишається належним чином нормалізовані.

Q10

У прикладі 3.5.1 описано рух об'єкта, що має постійне власне прискорення$a$, світову лінію$t = \frac{1}{a} \sinh a\tau$ і$x = \frac{1}{a} \cosh a\tau$ координати Мінковського певного спостерігача.

1. Доведіть наступні результати для$γ$ і для (три-) швидкості і (три-) прискорення вимірюється цим спостерігачем. $$\gamma =\cosh a\tau \\ v = \tanh a\tau \\ \text{acceleration} = a\cosh ^{-3}a\tau$$ Робити розрахунки просто взявши першу і другу похідні позиції щодо часу. Ви знайдете наступні факти корисними: $$1-\tanh ^2 = \cosh ^{-2}\\ \frac{\mathrm{d} }{\mathrm{d} x} \tanh = \cosh ^{-2}x$$
2. Інтерпретувати результати в межі великих$τ$.

Q11

У прикладі 3.5.1 описано рух об'єкта, що має постійне власне прискорення$a$, світову лінію$t = \frac{1}{a} \sinh a\tau$ і$x = \frac{1}{a} \cosh a\tau$ координати Мінковського певного спостерігача. Знайдіть відповідні швидкості і прискорення чотири-вектори.

Q12

Виходячи з результатів завдання Q11, повторіть задачу Q10a, використовуючи методи розділу 3.7. Вам буде корисно це знати$1-\tanh ^2 = \cosh ^{-2}$.

Q13

$v$Дозволяти бути спрямованим на майбутнє, правильно нормованим вектором швидкості. Порівняйте значення$v\cdot v$ в$+---$ підписі, використаному в цій книзі, з його значенням в підписі$-+ ++$.

Q14

1. Доведіть відношення$\frac{\mathrm{d} \gamma }{\mathrm{d} t} = \gamma ^3 a_o\cdot v_o$, в особливому випадку, коли рух є лінійним.
2. Узагальнити результат до$3 + 1$ розмірів.

Q15

Вивести особистість$a_o = \frac{1}{(o\cdot v)^2}\left [ P_o a - (o\cdot a)v_a \right ]$.

Q16

Рекапітулюючи геометрію на малюнку нижче, нехай$W$ буде плавна, схожа на час$E$ світова лінія$W$, подія не на, і$r$ вектор від$E$ до точки на$W$, параметризований належним часом$τ$. Визначте належну відстань$l$ між$E$ і точкою на$W$ як$l^2 = -(P_v r)^2$, де квадрат вказує внутрішній добуток вектора з собою, а знак мінус тому, що ми використовуємо$+---$ підпис. Покажіть$\frac{\mathrm{d} l^2}{\mathrm{d} \tau } = 2(r\cdot v)(r\cdot a)(v\cdot v)$, що там, де кінцевий фактор є лише підписом залежним знаком. Чи має це сенс, коли$W$ інерційний? Наведіть приклад, коли похідна зникає, оскільки перший множник дорівнює нулю, і інший приклад, коли другий фактор - це той, який зникає (але$a \neq 0$).

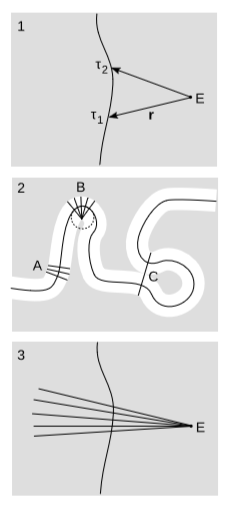
Q17

Розглянемо спостерігача, що$O$ рухається вздовж світової лінії$W$ з рухом постійного прискорення, визначеним у прикладі 3.5.1. У розділі 3.9 ми дали координати певної події$E$, яка ніколи не була «зараз», як описано нашим спостерігачем. Мета цієї проблеми полягає в тому, щоб проаналізувати це більш витончений і координатно-інваріантний спосіб. $P$Дозволяти точка на$W$, нехай$B$ буде подія, описана в розділі 3.9, і нехай$x = \overrightarrow{BP}$$h = \overrightarrow{BE}$, і$r = \overrightarrow{EP}$.

1. Показати те$W$, що, яке спочатку було описано в певному наборі координат, можна замість того, щоб визначити той факт, що$x\cdot v = 0$ для кожної точки на$W$.
2. Покажіть,$h$ що якщо timelike, то ніколи не$r\cdot v$ дорівнює нулю.