Skip to main content
LibreTexts - Ukrayinska

2.E: Основи (вправи)

  1. Last updated
  2. Save as PDF
  • Page ID
    77260

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Q1

    Розділ 2.5 дає аргумент, що просторово-часова область є релятивістським інваріантом. Чи є цей аргумент справедливим і для галілейської відносності?

    Q2

    Розділ 2.5 дає аргумент, що просторово-часова область є релятивістським інваріантом.

    1. Узагальнити це від\(1+1\) розмірів до\(3+1\).
    2. Використовуйте цей результат, щоб довести, що немає ефекту релятивістської довжини кон-тяги вздовж осі, перпендикулярної швидкості.

    Q3

    Мета цієї проблеми полягає в тому, щоб знайти, як напрямок фізичного об'єкта, такого як палиця, змінюється під час перетворення Лоренца. Частина b задачі Q2 показує, що релятивістське скорочення довжини відбувається тільки уздовж осі, паралельної руху. Узагальнення\(1 + 1\) - розмірного перетворення Лоренца в\(2 + 1\) розміри тому складається просто з збільшення рівняння 1.4.1 в розділі 1.4 с\(y'=y\). Припустимо, що палиця, у власному кадрі відпочинку, має один кінець зі світовою лінією,\((\tau , 0, 0)\) а інший з\((\tau , p, q)\), де\(\tau\) є належний час палиці. Назвіть ці кінці\(A\) і\(B\). Іншими словами, у нас є палиця, яка йде від початку до координат\((p, q)\) в\((x, y)\) площині. Застосуйте перетворення Лоренца для прискорення зі швидкістю\(v\) у напрямку x та знайдіть рівняння світових ліній кінців палиці в нових\((t', x', y')\) координатах. Відповідно до поняття одночасності цього нового кадру, знайдіть координати,\(B\) коли\(A\) знаходиться в\((t', x', y')= (0, 0, 0)\).

    1. В особливому випадку\(q \neq 0\), коли, відновити\(1 + 1\) - вимірний результат для скорочення довжини, наведеного в розділі 1.3.
    2. Повертаючись до загального випадку\(q \neq 0\), де, розглянемо кут,\(\theta\) який паличка робить з\(x\) віссю, і пов'язаний кут,\(\theta ' \) який вона робить з\(x'\) віссю в новому кадрі. Покажіть, що\(tan(\theta ') = \gamma tan(\theta)\)

    Q4

    У розділі 2.2 обговорюється ідея про те, що двовимірна помилка, що живе на поверхні сфери, може сказати, що її простір вигнутий. На малюнку 2.2.2 в розділі 2.2 показаний один із способів розповіді, шляхом виявлення шляху- залежності паралельного транспорту. Іншою методикою було б пошук порушень теореми Піфагора. На малюнку 2.E.1 нижче, 1 - діаграма, що ілюструє доказ теореми Піфагора в Елементах Евкліда (розділ 2.2/2.3). Ця діаграма однаково дійсна, якщо сторінка згорнута на циліндр, 2, або сформована в хвилясту рифлену форму, 3. Ці види кривизни, яких можна досягти без розриву або м'яття поверхні, не є реальними для клопа. Вони є просто побічними ефектами візуалізації його двовимірного Всесвіту так, ніби вона була вбудована в гіпотетичний третій вимір - який не існує в жодному сенсі, який емпірично піддається перевірці помилки. З криволінійних поверхонь на малюнку лише сфера, 4, має кривизну, яку може виміряти помилка; діаграму не можна оштукатурити на сферу без складання або різання та наклеювання. Якби двовимірна істота жила на поверхні конуса, чи скаже це, що його простір вигнутий, чи ні? А як щодо форми сідла?

    рис. 2.E.1.png
    Малюнок 2.E.1

    Q5

    Розбіжність паралельного транспорту, показану на малюнку 2.2.2 в розділі 2.2, також можна інтерпретувати як міру кутового дефекту трикутника\(d\), тобто величину,\(S - \pi\) на яку сума його внутрішніх кутів\(S\) перевищує евклідову величину.

    1. Малюнок пропонує простий спосіб перевірки того, що кутовий дефект трикутника, вписаного на сферу, залежить від площі. На ній зображений великий рівносторонній трикутник, який був розсічений на чотири менших трикутника, кожен з яких також приблизно рівносторонній. Доведіть\(D = 4d\), що, де\(D\) кутовий дефект великого\(d\) трикутника і значення для одного з чотирьох менших.
    2. Враховуючи, що пропорційність площі\(d = kA\) тримається в цілому, знайдіть якийсь трикутник на сфері радіуса, площа\(R\) якого і кутовий дефект легко обчислити, і використовувати його для фіксації константи пропорційності\(k\).
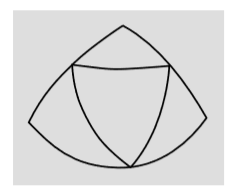
    рис. 2.e.2.png
    Малюнок 2.E.2

    Зауваження: Істота, яка жила на сфері, могла виміряти\(d\) і\(A\) для якогось трикутника і зробити висновок\(R\), що є мірою кривизни. Пропорційність ефекту площі трикутника також має на увазі, що наслідки кривизни стають незначними на досить малих масштабах. Аналогія в теорії відносності полягає в тому, що спеціальна відносність є дійсним наближенням до загальної відносності в областях простору, які є досить малими, так що кривизна простору-часу стає незначною.