2.2: Площинність

Last updated

Oct 27, 2022
Save as PDF
- 2.1: Причинність
- 2.3: Додаткові постулати

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Вивчення поняття паралельного транспорту
Площинність простору/часу

провал паралелізму

У Постулаті P1 ми неявно припустили, що з урахуванням двох точок існує певний вектор, що з'єднує їх. Це аналогічно евклідовому постулату про те, що дві точки визначають лінію. Для розуміння давайте подумаємо про те, як евклідова версія цього припущення могла зазнати невдачі. Евклідова геометрія - це лише приблизний опис земної поверхні, наприклад, і саме тому плоскі карти завжди тягнуть за собою спотворення реальних форм. Спотворення можуть бути незначними на карті Коннектикуту, але серйозними для карти всього світу. Тобто земна куля тільки локально евклідова. На сферичній поверхні відповідним об'єктом, який грає роль «лінії», є велике коло, рис $\PageIndex{1}$ . Лінії довготи є прикладами великих кіл, і оскільки всі вони збігаються на полюсах, ми бачимо, що дві точки не визначають лінію в неевклідовій геометрії.

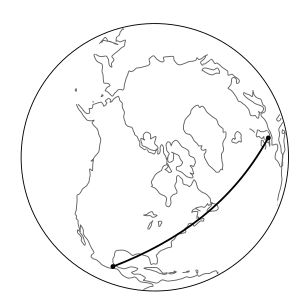
2.2.1.PNG — Малюнок $\PageIndex{1}$ : Літак, що летить з Мехіко в Лондон, йде найкоротшим шляхом, який є відрізком великого кола. Шляху екстремальної довжини між двома точками називають геодезичним.

Двовимірна помилка, що живе на поверхні сфери, не зможе сказати, що сфера була вбудована в третій вимір, але все одно може виявити кривизну поверхні. Це може сказати, що постулати Евкліда були помилковими на великих дистанційних масштабах. Метод, який має кращий аналог у просторовічасі, показаний на малюнку $\PageIndex{2}$ : транспортування вектора з однієї точки в іншу залежить від шляху, по якому він транспортувався. Цей ефект є нашим визначенням кривизни.

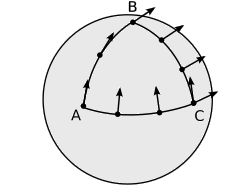
Малюнок $\PageIndex{2}$ : Транспортування вектора вздовж контуру $\overrightarrow{AC}$ дає інший результат, ніж виконання його вздовж шляху ABC.

Паралельний транспорт

Особливий вид транспорту, який ми маємо на увазі тут, називається паралельним транспортом. Коли я йду з вітальні на кухню, несучи механічний гіроскоп, я паралельно транспортую космічний вектор, позначений напрямком його осі. $\PageIndex{3}$ На малюнку показано, що паралельний транспорт також може бути визначений для часових векторів, і що паралельний транспорт можна визначити в простору-часі, використовуючи лише інерційний рух, годинник та перетин світових ліній. Спостерігачі на борту двох космічних кораблів використовують годинник для того, щоб перевірити паралельність своїх світових ліній (вектори $\overrightarrow{AB}$ та $\overrightarrow{CD}$ , які мають однакову довжину, виміряну належним часом, що минув на борту кораблів). Спостерігач $\overrightarrow{AB}$ знімає годинник до спостерігача $\overrightarrow{CD}$ , а годинник налаштовані так, що, проходячи повз одного, вони автоматично записують показання один одного. Вектори паралельні, якщо запис пізніше виявляє $\overrightarrow{AD}$ та $\overrightarrow{BC}$ перетинається в їх середніх точках, як вимірюється належним часом, записаним на годиннику.

2.2.2_d.png — Малюнок $\PageIndex{3}$ : Паралельний транспорт.

Спеціальна відносність вимагає плоского простору/часу

Прихованим у ряді плям у главі 1 було наступне припущення.

Постулат 2 (P2): Площинність простору-часу

Паралельно-транспортування вектора з однієї точки в іншу дає результат, незалежний від шляху, по якому він транспортувався.

Властивість P2 є лише приблизно вірною, як явно показав супутник Gravity Probe B, запущений у 2004 році. Зонд ніс чотири гіроскопи, виготовлені з кварцу, які були найдосконалішими сферами, коли-небудь виготовленими, варіюючись від сферичності не більше ніж на $40$ атоми. Через рік і близько $5000$ орбіт навколо землі було виявлено, що гіроскопи змінили свою орієнтацію щодо далеких зірок приблизно на $3 \times 10^{-6}$ радіани (малюнок $\PageIndex{4}$ ). Це порушення Р2, але таке, яке було дуже мало і важко виявити. Результат був добре узгоджений з прогнозами загальної відносності, яка описує гравітацію як кривизну простору-часу. Малість ефекту говорить нам про те, що гравітаційне поле землі не настільки велике, щоб повністю знешкодити спеціальну відносність як опис сусідньої області просторучасу.

Одне з основних припущень загальної відносності полягає в тому, що в досить невеликій області простору-часу завжди є хорошим наближенням припустити P2, так що загальна відносність локально така ж, як спеціальна відносність. В експерименті Gravity Probe B ефект був невеликим і важко виявити, і це стало причиною того, що ефект накопичувався на великій кількості орбіт, що охоплюють велику область простору-часу. Задача Q5 в розділі вправ досліджує більш кількісно, як розмір ефектів кривизни змінюється залежно від розміру області.

2.2.2_e.png — Рисунок $\PageIndex{4}$ : Кут прецесії як функція часу, виміряний чотирма гіроскопами на борту гравітаційного зонда B.