Skip to main content
LibreTexts - Ukrayinska

2.5: Лемма - Просторово-часова область інваріантна

  1. Last updated
  2. Save as PDF
  • Page ID
    77259

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    • Довести з аксіом Р1 - Р6, що площа в\(x - t\) площині інваріантна

    У цьому розділі з аксіом Р1-Р6 доведено, що площа в\(x - t\) площині є інваріантною, тобто вона не змінюється між рамками відліку. Цей результат був використаний у розділі 1.3 для пошуку форми метрики простору-часу. Розглянемо цифру\(\PageIndex{1}\).

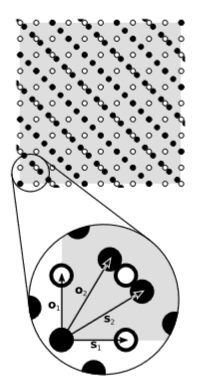
    рис. 2.5.1.png
    Малюнок\(\PageIndex{1}\): Площа є скаляром.

    Вектори\(\overrightarrow{o_1}\) і\(\overrightarrow{s_1}\) є ортогональними і мають однакову довжину, виміряну годинником і лінійкою (які калібруються в одиницях таких\(c = 1\), що, наприклад, секунди і світлові секунди). Квадратна решітка з білих горошок виходить з них шляхом багаторазового додавання. Припускаючи, що ця конструкція решітки можлива, ми неявно припускаємо постулат P2, площинність просторучасу.

    Такі ж властивості тримаються для векторів\(\overrightarrow{o_2}\) і\(\overrightarrow{s_2}\), які дають решітку чорних крапок. У міру необхідності дві решітки узгоджуються за своїми\(45\) -градусними діагоналями. Тепер в межах\(10 × 10\) частини білої решітки, показаної сірим відтінком, у нас є область\(100\). У тому ж регіоні ми підраховуємо близько\(100\) або\(101\) чорні точки — є певна неоднозначність через точки, які лежать на кордоні. Щільність білих і чорних крапок насправді точно рівна, як можна перевірити з будь-якою бажаною точністю, зробивши область досить великою. Іншими словами, діаграма намальована так, щоб площа збереглася, що ми збираємося показати потрібно. Якби це був спостерігач,\(2\) а не той,\(1\) хто малював діаграму, імовірно, вона вирішила б намалювати чорні точки у квадратній решітці та векторах\(\overrightarrow{o_2}\) та\(\overrightarrow{s_2}\) під прямим кутом. Для цього потрібні вектори\(\overrightarrow{o_2}\) і\(\overrightarrow{s_2}\) повинні бути відкриті під косим кутом, а біла решітка повинна бути неквадратною.

    Тепер припустимо, ми не зробили площа консервованої. Що робити, якщо регіон, що містить\(100\) білі точки, мав\(200\) чорні? Підрахунок точок - це те, як спостерігачі визначають область, тому, якщо це сталося, їм доведеться погодитися, що прискорення\(v\), від кадру\(1\) до кадру\(2\), подвоїло площу сірої області. Оскільки spacetime є плоским (P2) і однорідним (P3), можна взяти геометричну форму, вписану в певну область просторучасу, і переміщати, обертати або перевертати її. І за ізотропією простору (P3), приріст швидкості\(v\) такий же, як фліп просторового виміру з подальшим\(-v\) імпульсом та іншим перевертанням. Площа зберігається фліпом, тому ми виявляємо, що прискорення\(-v\), від кадру\(2\) до кадру\(1\), також подвоює площу. Таким чином,\(+v\) поштовх з подальшим підвищенням призведе до чотириразового\(-v\) збільшення площі. Але пара рівних і протилежних підсилень скасовує, так що це протиріччя. Ми робимо висновок, що якщо ці принципи симетрії дотримуються, то просторово-часова площа однакова для будь-яких двох спостерігачів, тому вона є інваріантною.

    Це може здатися надмірно незграбним, що ми використовували ідею підрахунку точок у вищезгаданому аргументі, але пам'ятайте, що наше основне використання цього результату полягає у отриманні форми метрики, і до того, як метрика була знайдена, у нас не було системи вимірювання відносності, тому ми мали лише дуже примітивні методи на нашому утилізація.