1.E: Просторовий час (вправи)

Q1

Космонавти в трьох різних космічних кораблів спілкуються один з одним. Ті, хто знаходиться на борту кораблів$A$ і$B$ погоджуються про швидкість, в яку проходить час, але вони не згодні з тими, що знаходяться на кораблі$C$.

1. Аліса на борту корабля$A$. Як вона описує рух власного корабля, в його рамках відліку?
2. Опишіть рух двох інших кораблів відповідно до Аліси.
3. Дайте опис по Бетті, чия рамка відліку - корабель$B$.
4. Зробіть те ж саме для Кеті, на борту корабля$C$.

Q2

Що відбувається в рівнянні для$\gamma$ when you put in a negative number for $v$? Explain what this means physically, and why it makes sense.

Q3

$1$Космічний зонд «Вояджер», запущений в 1977 році, рухається швидше відносно землі, ніж будь-який інший створений людиною об'єкт, зі швидкістю$17,000$ метрів в секунду.

1. Обчисліть зонди$\gamma$.
2. Протягом одного року на землі на зонді проходить трохи менше одного року. Наскільки менше? (Є$31$ мільйон секунд на рік.)

Q4

Земля обертається навколо Сонця, і тому скорочується релятивістично у напрямку його руху. Обчислити величину, на яку зменшується його діаметр в цьому напрямку.

Q5

На малюнку показані сім векторів зміщення в просторі/часі. Які з них являють собою просторовічасові інтервали, які рівні один одному?

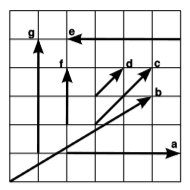
Q6

1. У евклідовій геометрії в трьох вимірах, припустимо, ми маємо два вектори,$a$ and $b$, which are unit vectors, i.e., $a \cdot a = 1$ and $b \cdot b = 1$. What is the range of possible values for the inner product $a \cdot b$?
2. Повторіть частину a для двох часових, орієнтованих на майбутнє одиничних векторів у$3 + 1$ dimensions.

Q7

Виражається в природних одиницях, перетворення Лоренца є

$$t' = \gamma t - v\gamma x' \\ x' = -v\gamma t + \gamma x$$

1. Вставити коефіцієнти$c$ to make it valid in units where \(c \neq 1\).
2. Покажіть, що в межі$c \rightarrow \infty$, вони мають кільце хіт Галілейська поведінка.

Q8

Ця проблема передбачає, що ви володієте деякими базовими знаннями з квантової фізики. Один із способів вираження принципу відповідності, застосованого до спеціальної відносності, полягає в тому$c \rightarrow \infty$, що в межі всі релятивістські вирази повинні перейти до своїх галілейських колег. Якою була б відповідна межа, якби ми хотіли відновити класичну механіку з квантової механіки?

Q9

У$3 + 1$ вимірах доведіть, що якщо$\overrightarrow{u}$ і$\overrightarrow{v}$ є ненульовими, майбутніми світлоподібними, а не паралельними один одному, то їх сума є майбутнім часом.

Q10

Доведіть, що якщо$\overrightarrow{u}$ і$\overrightarrow{v}$ ненульові, світлоподібні, і ортогональні один до одного, то вони паралельні, тобто$\overrightarrow{u} = c \overrightarrow{v}$ для деяких$c \neq 0$.

Q11

Швидкість, з якою порушення рухається уздовж струни під напругою,$\mu$ задається$v = \sqrt{\frac{T}{\mu}}$, де - маса на одиницю довжини, і$T$ є натягом.

1. Припустимо, струна має щільність$\rho$, а площа поперечного перерізу A. знайти вираз для максимального натягу, яке могло б існувати в струні без вироблення$v > c$, що неможливо відповідно до відносності. Висловіть свою відповідь з точки зору$\rho$, А, і$c$. Тлумачення полягає в тому, що відносність ставить межу на те, наскільки міцним може бути будь-який матеріал.
2. Кожна речовина має міцність на розрив, визначену як сила на одиницю площі, необхідну для її розриву, витягнувши її. Міцність на розрив вимірюється в одиницях$N/m^2$, що таке ж, як і паскаль ($Pa$), мкс одиниця тиску. Зробити числову оцінку максимальної міцності на розрив, дозволеної відносністю в тому випадку, коли мотузка зроблена зі звичайної матерії, з щільністю на тому ж порядку, що і у води. (Для порівняння, кевлар має міцність на розрив близько$4 \times 10^9\: Pa$, і є припущення, що волокна, виготовлені з вуглецевих нанотрубок, можуть мати значення настільки ж високими, як$6 \times 10^{10}\: Pa$.)
3. Чорна діра - це зірка, яка зруйнувалася і стала дуже щільною, так що її гравітація занадто сильна, щоб що-небудь коли-небудь втекти від неї. Наприклад, швидкість втечі з чорної діри більша$c$, тому снаряд не може бути вистрілений з неї. Багато людей, коли вони чують цей опис чорної діри з точки зору швидкості втечі, більшої$c$, ніж, дивуються, чому все ще не можна було б витягти об'єкт з чорної діри іншими способами, ніж запустити його як снаряд. Наприклад, припустимо, ми опускаємо космонавта в чорну діру на мотузці, а потім знову витягуємо його назад. Чому це може не спрацювати?

Q12

Вудилище на фігурі ідеально жорстке. На заході$A$, the hammer strikes one end of the rod. At event $B$, the other end moves. Since the rod is perfectly rigid, it can’t compress, so $A$ and $B$ are simultaneous. In frame $2$, $B$ happens before $A$. Did the motion at the right end змусити людину зліва прийняти рішення взяти в руки молоток і використовувати його?

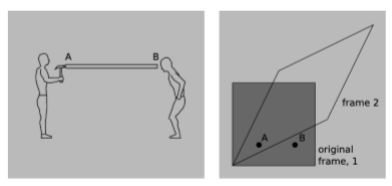
Q13

Використовуйте діаграму просторового часу, щоб вирішити наступний парадокс відносності. Відносність говорить про те, що в одному кадрі відліку подія$A$ could happen before event $B$, but in someone else’s frame $B$ would come before $A$. How can this be? Obviously the two people could meet up at $A$ and talk as they cruised past each other. Wouldn’t they have to agree on whether $B$ had already happened?

Q14

The grid represents spacetime in a certain frame of reference. Event $A$ is marked with a dot. Mark additional points satisfying the following criteria. (Pick points that lie at the intersections of the gridlines.)

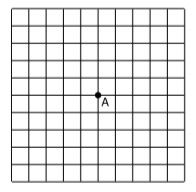
Точка$B$ is at the same location as $A$ in this frame of reference, and lies in its future.
$C$ is also in point $A$’s future, is not at the same location as $A$ in this frame, but is in the same location as $A$ according to some other frame of reference.
$D$ is simultaneous with $A$ in this frame of reference.
$E$ is not simultaneous with $A$ in this frame of reference, but is simultaneous with it according to some other frame.
$F$ lies in $A$’s past according to this frame of reference, but could not have caused $A$.
$G$ lies in $A$’s future according to this frame of reference, but is in its past according to some other frames.
$H$ lies in $A$’s future according to any frame of reference, not just this one.
$I$ is the departure of a spaceship, which arrives at $A$.
$J$ could have caused $A$, but could not have been the departure of a spaceship like $I$ that arrived later at $A$.

Q15

1. Враховуючи спостерігача, чия світова лінія знаходиться вздовж чотирьох-вектора$\overrightarrow{O}$, припустимо, ми хочемо визначити, чи$\overrightarrow{P}$ є якийсь інший чотиривекторний також можливою світовою лінією спостерігача. Покажіть, що знання ознак внутрішніх продуктів$\overrightarrow{O} \cdot \overrightarrow{P}$ і$\overrightarrow{P} \cdot \overrightarrow{P}$ необхідно і достатньо для цього визначення.
2. Припустимо, що$\overrightarrow{U}$ і$\overrightarrow{V}$ є обома спостерігачами-векторами. Що б означати фізично обчислювати$\overrightarrow{U} + overrightarrow{V}$?
3. Для векторів, описаних в частині b, визначте ознаки $$(\overrightarrow{U} + \overrightarrow{V}) \cdot (\overrightarrow{U} + \overrightarrow{V})$$ і $$(\overrightarrow{U} + \overrightarrow{V}) \cdot \overrightarrow{U}$$ шляхом їх множення. Інтерпретуйте результат фізично.

Q16

У розділі 1.5 ми довели зворотну нерівність Коші-Шварца для двох часових векторів, без будь-яких припущень щодо того, чи лежать вони в майбутньому чи минулих світлових конусах. Але припустимо, що ми встановили цей факт лише для двох векторів, які були спрямовані на майбутнє. Покажіть, що однакова нерівність тоді також доведеться утримувати незалежно від того, чи один або обидва вектори були спрямовані на минуле.

Q17

У випадку двох векторів, орієнтованих на майбутнє, завершіть доказ зворотної нерівності трикутника за допомогою методу, запропонованого в розділі 1.5.

Q18

У розділі 1.5 ми стверджували, що зворотна нерівність Коші-Шварца тримається для двох просторових векторів, які охоплюють світловий конус. Метою цієї задачі є доведення цього факту за допомогою наступного ескізу аргументу, наданого користувачем PhysicsForums martinbn. Припустимо, що просторові вектори$\overrightarrow{m}$ і$\overrightarrow{n}$ охоплюють світловий конус, так що ми можемо знайти деяке дійсне число$\alpha$ таких, що$p = \alpha m + n$ є lightlike. Обчислити$p^2$, і показати, що оскільки$\alpha$ є реальним, зворотна нерівність Коші-Шварца тримає.

КВАРТАЛ 19

Об'єкт, що стискається довжиною, має довжину$L = \frac{L_0}{\gamma}$ Джо диференціює це щодо часу та знахідок$\frac{dL}{dt} = −L_0v\gamma\frac{dv}{dt}$. Він міркує, що немає верхньої межі по величині$\frac{dv}{dt}$, а значить, якщо$v \neq 0$ кількість$\frac{dL}{dt}$ може бути як завгодно великим. Це означає, що якщо об'єкт прискорюється від спостерігача, його кінцевий край може мати$v > c$, що, як передбачається, заборонено відносністю. ОМГ! Чи правильні міркування Джо?