Skip to main content
LibreTexts - Ukrayinska

1.2: Координати Мінковського

  1. Last updated
  2. Save as PDF
  • Page ID
    77315

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    • Визначте координати Мінковського
    • Побудувати координати Мінковського на графічному папері

    Часто зручно називати точки у просторовічасі за допомогою координат, а певний тип іменування, обраний Ейнштейном та Мінковським, є типовим у спеціальній теорії відносності. Я буду посилатися на координати цієї системи як координати Мінковського, і вони є те, що я маю на увазі протягом цієї книги, коли я використовую літери, як\(t\) і\(x\) (або варіації\(x_0\), як\(t_0\), і т.д.) без подальшого пояснення. Щоб визначити координати Мінковського в\(1 + 1\) розмірах, нам потрібно вибрати:

    1. Подія, яку ми вважаємо походженням,\((t,x) = (0,0)\)
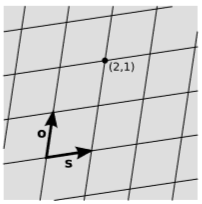
    2. Вектор-спостерігач\(o\)
    3. Сторона світової лінії спостерігача, яку ми будемо називати\(x\) позитивною стороною, і намалюємо праворуч на діаграмах.

    Спостерігач повинен бути інерційним, так що, неодноразово роблячи копії\(o\) і прокладаючи їх «кінчик до хвоста», ми отримуємо ланцюжок, яка лежить зверху світової лінії спостерігача і представляє галочки на годиннику спостерігача.

    Координати Мінковського використовують одиниці с\(c = 1\). Явно ми визначаємо унікальний вектор,\(s\) який є ортогональним до\(o\), вказує в позитивному напрямку і має довжину одного годинника. У практичному плані ортогональність може бути визначена синхронізацією Ейнштейна (приклад 1.1.4), а довжину, організувавши, що радіолокаційне відлуння рухається до кінчика\(s\) та назад у двох кліщах.

    рис. 1.2.1.png
    Ілюстрація\(\PageIndex{1}\): Герман Мінковський (18641909).

    Тепер ми будуємо графо-паперову решітку, фігуру\(\PageIndex{2}\), повторюючи вектори\(o\) і \(s\). Ця сітка визначає назву\((t,x)\) для кожної точки простору/часу. Загалом, ми живемо у Всесвіті з\(3\) просторовими розмірами або\(3 + 1\) розмірним простором часу, але координати легко дозволяють це узагальнення, замість цього вибираючи подію\((t_0, x_0, y_0, z_0) = (0, 0, 0, 0)\) як походження. Однак зауважте, що якщо цікаві явища відбуваються на одній лінії, то просторові частини системи координат завжди можна повернути так, що всі події відбуваються на\(x\) -осі, і ми можемо знову розглянути\(1 + 1\) простір. Це буде так для більшої частини книги, оскільки це дозволяє полегшити візуалізацію та математичний аналіз, а включення двох інших напрямків не особливо просвітлює в більшості випадків.

    рис. 1.2.2.png
    Малюнок\(\PageIndex{2}\): Набір координат Мінковського.