1.1: Три моделі простору-часу
- Page ID
- 77323
Цілі навчання
- Обговоріть три моделі простору-часу
- Аристотелівський простор-час
- Галілеєвий простор-час
- Простір-час Ейнштейна
«Тест першокласного інтелекту - це здатність тримати дві протилежні ідеї на увазі одночасно і все ще зберігати здатність функціонувати. » —Ф. Скотт Фіцджеральд
Час і простір разом складають простор. час, малюнок\(\PageIndex{1}\), етап, на якому розігрується фізика. До 1905 року фізики навчалися приймати дві взаємно суперечливі теорії простору-часу. Я буду називати ці погляди Аристотеля і Галілея, хоча мої колеги з тієї епохи були б ображені, щоб їх звинуватили в навіть частковому аристотеліанстві.
Аристотелівський простор-час
\(\PageIndex{2}\)На малюнку зображений спостерігач і два годинника, представлені за допомогою графічних умовностей рисунка\(\PageIndex{1}\) (3). Існування такого матеріального об'єкта в певному місці і часі являє собою подію, яку ми ідеалізуємо як точку, Рисунок\(\PageIndex{2}\) (2). Простір часу складається з безлічі всіх подій. З плином часу фізичний об'єкт простежує безперервну криву, сукупність подій, відомих в релятивістській мові як його світова лінія. Оскільки екрани паперу та комп'ютерів двовимірні, креслення представляють лише один вимір простору плюс один вимір часу, який у відносності ми називаємо «\(1+1\)розмірами». Реальний Всесвіт має три просторові виміри, тому реальний простор-час має\(3+1\) розміри. Більшість, але не всі, цікаві явища в особливій теорії відносності можна зрозуміти в\(1+1\) розмірах, тому по можливості в цій книзі я буду малювати\(1+1\) -мірні цифри без вибачень або пояснень.
Ставлення релятивіста полягає в тому, що події та відносини між подіями є первинними, тоді як координати, такі як\(x\) і\(t\) є вторинними і, можливо, не мають значення. Координати дозволяють нам прикріплювати мітки на кшталт (\(x,t\)) до точок, але це все одно, що Бог просить Адама назвати всіх птахів і тварин: тварини не дбали про імена. На малюнку\(\PageIndex{2}\) (3) показано використання векторів для позначення взаємозв'язків між точками. Вектор\(o\) - це спостерігач-вектор, що з'єднує дві точки на світовій лінії людини. Це вказує з минулого в майбутнє. Вектор s, що з'єднує два годинники, є вектором одночасності. Годинники раніше синхронізувалися пліч-о-пліч, і якщо ми припускаємо, що транспортування їх в окремі місця не порушує їх, то той факт, що обидва годинники читають дві хвилини після трьох годин, говорить нам про те, що дві події відбуваються одночасно.
Аристотельська модель просторучасу характеризується набором правил про те, які вектори є дійсними векторами спостерігача та одночасності. Ми вимагаємо, щоб кожен\(o\) вектор був паралельний кожному іншому, а також для\(s\) векторів. Але, як це зазвичай з векторами, ми дозволяємо малювати стрілку в будь-якому місці, не враховуючи різні місця, щоб мати якесь значення; тобто наша модель простору-часу не дозволяє різним регіонам мати різні властивості.
Коли Ейнштейн був студентом університету, ці правила (сформульовані по-різному) були тими, що його навчили використовувати при описі електрики та магнетизму. Пізніше він згадував, як уявляв себе на мотоциклі, їхав поруч зі світлою хвилею і намагався уявити, як його спостереження можна примирити з рівняннями Максвелла. Я не знаю, чи був він коли-небудь достатньо сміливим, щоб описати цю мрію своїм професорам, але якби він мав, їхня відповідь була б по суті, що його гіпотетичний\(o\) вектор був незаконним. Вважалося, що хороші\(o\) вектори представляли спостерігача в спокої відносно ефіру, гіпотетичного всепроникаючого середовища, коливання якого були електромагнітними хвилями. Як би нерозумно це не здавалося нам через сто років, насправді це було сильно підтверджено доказами. Величезна кількість експериментів перевірила достовірність рівнянь Максвелла, і було відомо, що якби рівняння Максвелла були дійсними в координатах (\(x,t\)), визначених спостерігачем\(o\), вони стануть недійсними при перетворенні на\((x', t') = (x + vt, t)\) координати, визначені спостерігачем\(o'\) в русі зі швидкістю\(v\) відносно\(o\).
Галілеєвий простор-час
Але вже було відомо, що модель Аристотеля помиляється при застосуванні до матеріальних предметів. Класична емпірична демонстрація цього факту прийшла приблизно в 1610 році з відкриттям Галілея чотирьох супутників, що обертаються навколо Юпітера, рис\(\PageIndex{4}\). Аристотелізм у стародавньому вигляді спочатку був придуманий як пояснення того, чому предмети завжди здавалося, осідають до природного стану спокою за словами спостерігача, що стоїть на земній поверхні. Але коли Юпітер літав через небо, його супутники кружляли навколо нього, не виявляючи природної тенденції відставати від нього, як паперовий стаканчик, викинутий у вікно автомобіля. Подібно до того, як спостерігач,\(o_1\) що стоїть на землі, вважав би землю в спокої,\(o_2\) зависаючи на повітряній кулі на вершині хмар Юпітера, сказав би, що Джовіанські хмари представляли однаково «природний» стан спокою.
Малюнок\(\PageIndex{4}\): Моделювання того, як Юпітер та його супутники можуть з'являтися з інтервалом у три години через телескоп. Оскільки ми бачимо кругові орбіти Місяця на краю, їх світові лінії виглядають синусоїдальними. За цей часовий проміжок, найпотаємніша місяць\(Io\), завершує півциклу.
Таким чином, ми привели до іншого, галілейського, набору правил для\(o\) і\(s\) векторів. Всі\(s\) вектори паралельні один одному, але будь-який вектор\(t\) не паралельний\(s\) вектору є дійсним\(o\) вектором. (Ми можемо вимагати, щоб він вказував на майбутнє, а не минуле, але закони Ньютона симетричні під час зміни часу, тому це не є суворо необхідним.)
Галілея просторучасу, на відміну від Аристотелівськогочасу, не має універсального поняття «те саме місце». Я можу поїхати до Геттісбурга, штат Пенсільванія, і стояти перед латунною дошкою, яка позначає місце знаменної битви Громадянської війни. Але чи справді я в одному місці? Спостерігач на іншій планеті сказав би, що наша планета рухалася через космос з 1863 року.
Паралелізм
Зауважте, що наш геометричний опис включає поняття паралелізму, але не кутової міри. Ми не знаємо і не хвилює, чи\(o\) є «кут» між a\(s\) і an\(90\) градуси. Один представляє відстань, а інший - проміжок часу, і ми не можемо визначити кут між відстанню і часом. Те ж саме було і в моделі Аристотеля; вектори на Fgure\(\PageIndex{3}\) були намальовані перпендикулярно один одному просто як умова, але будь-який інший кут міг бути використаний.
Парадокс близнюків Галілея
Аліса і Бетті - однакові близнюки. Бетті відправляється в космічну подорож, подорожуючи від землі вздовж вектора,\(o_1\) а потім обертаючись і повертаючись назад\(o_2\). Тим часом Аліса залишається на землі. Оскільки це експеримент із залученням матеріальних об'єктів, і умови подібні до тих, при яких відносність Галілея неодноразово перевірялася експериментом, ми очікуємо, що результати будуть узгоджуватися з твердженням галілейської відносності про те, що рух є відносним. Тому здається, що слід однаково справедливо вважати Бетті та космічний корабель, що весь час перебували у спокої, тоді як Аліса та планета Земля подорожували від космічного корабля,\(o_3\) а потім повернулися через\(o_4\). Але це не узгоджується з експериментальними результатами, які показують, що Бетті зазнає бурхливого прискорення у своїй точці повороту, тоді як Аліса та інші мешканці землі не відчувають такого ефекту.
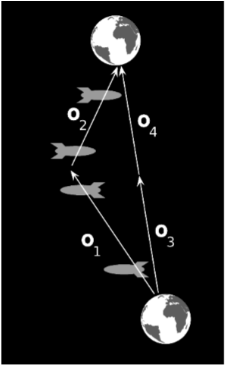
Парадокс вирішується, розуміючи, що Галілеєва відносність однозначно визначає, чи два вектори паралельні чи ні. Це правда, що ми могли б виправити систему відліку, в якій\(o_1\) представлений космічний корабель, який залишається в стані спокою, але\(o_2\) не паралельно\(o_1\), тому в цьому кадрі ми все ще маємо гарне пояснення того, чому Бетті відчуває прискорення: вона перейшла від спокою до руху. Незалежно від того, яку систему відліку ми вибираємо, і незалежно від того, чи ми навіть фіксуємо систему відліку,\(o_3\) і\(o_4\) паралельні один одному, і це пояснює, чому Аліса не відчуває ніякого ефекту.
Простір-час Ейнштейна
У нас є дві моделі просторучасу, жодна з яких не здатна описати всі спостерігаються нами явища. Через відносно грубий стан технології близько 1900 року, Ейнштейну потрібно значне розуміння, щоб зібрати фрагментарне тіло непрямих доказів і прийти до послідовної та правильної моделі простору-часу. Сьогодні докази є частиною повсякденного життя. Наприклад, кожен раз, коли ви використовуєте GPS-приймач, ви використовуєте теорію відносності Ейнштейна. Десь між 1905 і сьогодні технології стали досить хорошими, щоб дозволити концептуально прості експерименти, які студенти на початку\(20^{th}\) століття могли обговорювати лише в таких термінами, як «Уявіть, що ми могли б... »
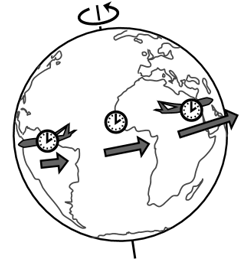
Хороша точка стрибка - 1971 рік. У тому році J.C. Hafele і R.E. Keating привезли атомні годинники на борту комерційних авіалайнерів, Фігуре\(\PageIndex{7}\), і поїхали по всьому світу, колись зі сходу на захід і один раз із заходу на схід. Хейфеле та Кітінг зауважили, що існує невідповідність між часом, виміряним годинниками, і часом, виміряним подібними годинниками, які залишилися вдома у Військово-морській обсерваторії США у Вашингтоні. Східний годинник втратив час, закінчуючись\(-59 \pm 10\) наносекундами, тоді як західний отримав\(273 \pm 7\) нс.
Ми звикли думати про час як про абсолютний і універсальний, тому тривожно виявити, що він може протікати з різною швидкістю для різних спостерігачів. Тим не менш, ефекти, які спостерігали Хафеле і Кітінг, були невеликими. Це має сенс: Галілейська відносність вже була ретельно перевірена для матеріальних об'єктів, таких як годинник, планети та літаки, тому нова теорія, як Ейнштейна, повинна була погодитися з Галілеєм на хороше наближення, в області застосовності теорії Галілея. Ця вимога зворотної сумісності відома як принцип відповідності.
Це також заспокоює, що вплив на час був невеликим порівняно з триденною тривалістю поїздок на літаку. Тому не було можливості для парадоксальних сценаріїв, таких як той, коли східний експериментатор приїхав назад до Вашингтона перед тим, як він поїхав, а потім переконався не їхати в поїздку. Теорія, яка підтримує такий впорядкований зв'язок між причиною та наслідком, як кажуть, задовольняє причинно-наслідковий зв'язок.
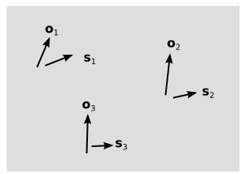
Хафеле та Кітінг тестували конкретні кількісні прогнози відносності, і вони перевіряли їх у межах смуг помилок свого експерименту. Давайте замість цього працюємо назад і перевіряємо емпіричні результати для підказок щодо того, як працює час. Розбіжності між годинниками говорять про те, що одночасність не є абсолютною: різні спостерігачі мають різні поняття одночасності, як це запропоновано на рис\(\PageIndex{9}\). Подібно до того, як Галілеєва відносність звільнила\(o\) вектори від обмеження бути паралельними один одному, Ейнштейн звільняє\(s\) вектори. Галілей зробив «те саме місце» в неоднозначну концепцію, тоді як Ейнштейн зробив те ж саме з «одночасним». Але оскільки конкретний спостерігач має методи синхронізації годинників (наприклад, синхронізація Ейнштейна, приклад\(\PageIndex{4}\)), визначення одночасності не є абсолютно довільним. Для кожного\(o\) вектора ми маємо відповідний\(s\) вектор, який представляє думку цього спостерігача щодо того, що являє собою одночасність. Оскільки угода на декартовому\(x - t\) графі полягає в тому, щоб намалювати осі під прямим кутом один до одного, ми називаємо таку пару векторів ортогональними, але слово не слід інтерпретувати буквально, оскільки ми не можемо визначити фактичний кут між часовим інтервалом і просторовим зміщенням.
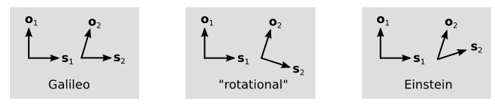
Які ж тоді правила ортогональності? На малюнку\(\PageIndex{10}\) показані три можливості. У кожному випадку ми маємо початкову пару векторів\(o_1\) і\(s_1\) що ми припускаємо, що є ортогональними, і ми потім малюємо нову пару\(o_2\) і\(s_2\) для другого спостерігача, який знаходиться в русі відносно першого. Справа Галілея, де\(s_2\) залишається паралельно\(s_1\), вже виключена. Другий випадок - той, в якому\(s\) обертається в тому ж напрямку, що і\(o\). Це заборонено причинністю, тому що якщо ми продовжуємо обертатися, ми могли б врешті-решт обертатися\(o\) на\(180\) градуси, тому, продовжуючи процес прискорення, ми могли б відправити спостерігача в стан, в якому її відчуття часу було скасовано. Нам залишається лише одна можливість для просторучасу Ейнштейна, який є тим, в якому обертання за годинниковою стрілкою\(o\) викликає обертання проти годинникової стрілки\(s\), як закриття пари ножиць.
Тепер існує межа того, наскільки далеко може пройти цей процес, інакше\(s\) і\(o\) врешті-решт ляже на тій же лінії. Але це неможливо, бо дійсний\(s\) вектор ніколи не може бути дійсним\(o\), ні\(o\) дійсним\(s\). Така можливість означатиме, що спостерігач описує дві різні точки на своїй власній світовій лінії як одночасні, але спостерігач, для якого не проходить часу, зовсім не є спостерігачем, оскільки спостереження передбачає збір даних, а потім можливість запам'ятати їх пізніше. Зроблено висновок, що існує діагональна лінія, яка утворює межу між множиною можливих\(s\) векторів і безліччю допустимих\(o\) векторів. Ця лінія має певний нахил, і зворотний цей нахил відповідає деякій швидкості, яка, мабуть, є універсальним і фіксованим властивістю простору-часу Ейнштейна. Цю швидкість ми називаємо\(c\), і принцип відповідності говорить нам, що вона\(c\) повинна бути дуже великою, тому що в іншому випадку Ейнштейнські, або «релятивістські» ефекти, такі як спотворення часу, були б великими навіть для руху на повсякденних швидкостях; в експерименті Хафель-Кітінга вони були досить малі, навіть на високій швидкості пасажирського літака.
Хоча\(c\) це велика кількість, коли виражається в метрах в секунду, для зручності в відносності ми завжди будемо вибирати одиниці такі, що\(c = 1\). Межа між\(o\) векторами\(s\) та векторами з'являється на діаграмах просторового часу у вигляді діагональної лінії в\(\pm 45\) градусах. У більш ніж одному просторовому вимірі ця межа утворює конус, фігуру\(\PageIndex{11}\), і з причин, які стануть більш чіткими в мить, цей конус називається світловим конусом. Вектори, що лежать всередині світлового конуса, називаються тимчасовими, ті, що зовні, як космічні, а ті, що знаходяться на самому конусі, як світлоподібні або нульові.
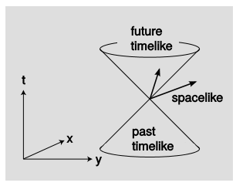
Важливою перевагою відносності Ейнштейна над Галілео є те, що вона сумісна з емпіричним спостереженням, що деякі явища подорожують з певною фіксованою швидкістю. Світло рухається з фіксованою швидкістю, як і інші явища, такі як гравітаційні хвилі (вперше безпосередньо виявлені в 2016 році). Так роблять всі безмасові частинки (підрозділ 4.3.4). Ця фіксована швидкість є\(c\), і всі спостерігачі погоджуються з нею. У 1905 році єдиним явищем, відомим для подорожі,\(c\) було світло, \(c\)тому його зазвичай описують як «швидкість світла», але з сучасної точки зору він функціонує більше як своєрідний коефіцієнт перетворення між нашими одиницями вимірювання часу та простору. Це властивість просторучасу, а не властивість світла.
Більш принципово,\(c\) це максимальна швидкість причинно-наслідкового впливу. Якби ми могли поширювати причину та наслідок, наприклад, передаючи сигнал, зі швидкістю більшою\(c\), то наступний аргумент показує, що ми порушуємо або причинність, або принцип, що рух є відносним. Якщо сигнал може поширюватися зі швидкістю більшою\(c\), то вектор, що \(r\)з'єднує причину та ефект, буде схожим на пробіл. Відкриваючи і закриваючи «ножиці» Фігури\(\PageIndex{10}\), ми завжди можемо знайти спостерігача\(o\), який вважає\(r\) вектором одночасності. Таким чином, якщо можливе поширення швидше, ніж світло, то миттєве поширення можливо, принаймні для деякого спостерігача. Оскільки рух є відносним, це повинно бути можливим для всіх спостерігачів, незалежно від їх стану руху. Тому будь-який spacelike вектор є одним, уздовж якого ми можемо посилати сигнал. Але додаючи два вектори, подібні до простору, ми можемо зробити вектор, що лежить в минулому часі, як світловий конус, тому, передаючи сигнал, ми могли б відправити повідомлення в минуле, порушуючи причинно-наслідковий зв'язок.
Інтерпретуючи цей аргумент, зверніть увагу, що ні відносність руху, ні причинність не є логічною необхідністю; вони обидва є лише узагальненнями, заснованими на сукупності доказів. Докладніше про причинно-наслідковий зв'язок та її невизначений емпіричний статус див. Розділ 2.1.
Кільцевий лазерний гіроскоп
Якщо ви літали в реактивному літаку, ви можете подякувати відносності за допомогу вам уникнути врізки в гору або океан. \(\PageIndex{12}\)На малюнку зображений стандартний шматок навігаційного обладнання, званий кільцевим лазерним гіроскопом. Промінь світла розбивається на дві частини, направляється по периметру приладу, і возз'єднується. Оскільки швидкість світла постійна, ми очікуємо, що дві частини повернуться разом одночасно. Якщо вони цього не роблять, це докази того, що пристрій обертається. Комп'ютер літака відчуває це і зазначає, скільки обертання накопичилося.

Без частоти - залежність
Відносність має тільки одну універсальну швидкість, тому вона вимагає, щоб всі світлові хвилі рухалися з однаковою швидкістю, незалежно від їх частоти і довжини хвилі. В даний час найкращі експериментальні випробування інваріантності швидкості світла щодо довжини хвилі походять від астрономічних спостережень гамма-сплеску, які є раптовими виливами високочастотного світла, які, як вважають, походять від вибуху наднової в іншій галактиці. Одне з таких спостережень, в 2009 році, виявило, що часи прибуття всіх різних частот у вибуху відрізнялися не більше ніж на\(2\) секунди із загального часу польоту близько десяти мільярдів років!
Поїзд Ейнштейна
\(\PageIndex{13}\)На малюнку показаний відомий експеримент думки, розроблений Ейнштейном. Поїзд рухається з постійною швидкістю вправо, коли болти блискавки вдаряються об землю біля її передньої і задньої частини. Аліса, стоячи на бруді в середній точці спалахів, зауважує, що світло від двох спалахів надходить одночасно, тому вона каже, що два удари, мабуть, відбулися одночасно. Боб, тим часом, сидить на борту поїзда, в його середині. Він проходить повз Алісу в той момент, коли Аліса пізніше з'ясовує, що спалахи сталися. Пізніше він отримує спалах\(2\), а потім спалах\(1\). Він робить висновок, що оскільки обидва спалаху пройшли половину довжини поїзда, спалах,\(2\) мабуть, стався першим. Як це можна змиритися з вірою Аліси в те, що спалахи були одночасними?
\(\PageIndex{14}\)На малюнку показана відповідна діаграма простору-часу. Здається парадоксальним, що Аліса і Боб розходяться в одночасності, але це тільки тому, що ми маємо вкорінене упередження на користь галілейської відносності. Метод Аліси визначення того, що\(1\) і\(2\) були одночасними, є дійсним, і відомий як синхронізація Ейнштейна. Пунктирна лінія, що\(2\) з'єднує\(1\) і є ортогональною до світової лінії Аліси. Але у Боба інша думка про те, що являє собою одночасність. Коса пунктирна лінія ортогональна його світовій лінії. За словами Боба,\(2\) сталося до часу, представленого цією лінією,\(1\) після.
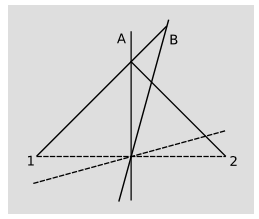
Приклад\(\PageIndex{4}\), звичайно, недоцільний, як описано, оскільки справжні поїзди не їздять зі швидкістю\(c\) десь поблизу бруду. Ми говоримо, що їх швидкості «нерелятивістські». Оскільки Ейнштейн придумав термін «відносність», а його версія відносності витіснила Галілея, немодифіковане слово зазвичай розуміється як позначення Ейнштейнської відносності. Фізик, який вивчає відносність Ейнштейна, є релятивістом. Матеріальний об'єкт, що рухається зі швидкістю, дуже близькою до,\(c\) описується як ультрарелятивістський. Часто чують мирян, що описують відносність з точки зору певних ефектів, які б трапилися «якби ви пішли зі швидкістю світла. Насправді, як ми побачимо в главі 3 та главі 4, неможливо прискорити матеріальні об'єкти\(c\), і в будь-якому випадку це не потрібно. Релятивістські ефекти існують на всіх швидкостях, але вони слабкі при малих швидкостях порівняно з\(c\).
Числове значення c
У цій книзі ми будемо використовувати одиниці, в яких\(c = 1\). Однак багатьох початківців турбує питання про те, чому\(c\) має особливе значення, яке він робить в даній системі одиниць, таких як СІ. З цим пов'язано питання про те, чи\(c\) може коли-небудь змінитися, так що вимірювання його сьогодні та вимірювання завтра дало б дещо інші результати. У системі одиниць, де\(c\) є одиниці, її значення є те, що це тільки через наш вибір одиниць, і немає значущого способу перевірити, чи змінюється вона.
Візьмемо СІ як приклад системи одиниць. SI спочатку був встановлений так, що лічильник і другий визначалися з точки зору властивостей нашої планети. Метр становив одну сорокамільйонну частину окружності землі, а другий був\(1/86,400\) середнього сонячного дня. Таким чином, коли ми виражаємо\(c\) як\(3.0 \times 10^8 m/s\), ми в основному вказуємо коефіцієнт, на який\(c\) перевищує швидкість, з якою точка на екваторі йде навколо центру землі (з додатковими коефіцієнтами перетворення\(40,000,000\) і\(86,400\) викинутих в). Оскільки властивості нашої планети є випадковістю формування Сонячної системи, немає фізичної теорії, яка могла б сказати нам, чому\(c\) має це значення в оригінальній французько-революційній версії СІ.
Базові одиниці СІ були переглянуті протягом століть. Сьогодні другий визначається з точки зору атомного стандарту, а вимірювач визначається як\(1/299,792,458\) світлова секунда. Тому \(c\)має певне значення точно\(299,792,458 m/s\). Знову ж таки, ми виявляємо, що числове значення не\(c\) має принципового значення; це лише питання визначення. Можна сформувати безодиничне співвідношення\(\alpha = e^2/\tilde{h} c \approx 1/137\), зване постійною тонкої структури. Його значення не залежить від нашого вибору одиниць, тому можна проводити експерименти, щоб шукати зміни його величини з плином часу, наприклад, порівнюючи спектр водню на землі зі спектром далеких зірок, світло яких зайняв мільярди років, щоб дістатися до нас. Навіть були висловлені претензії на те, що ці спостереження показують зміни, хоча це, здається, було помилкою. Якби така зміна відбулася, ми не змогли б однозначно приписувати це зміною,\(c\) а не зміною\(\tilde{h}\) або фундаментальним звинуваченням. Стандарти, що використовуються для визначення наших підрозділів, можуть змінюватися з часом. Підозрюється, що платино-іридієвий стандарт для кілограма в Парижі втратив близько\(50\) мкг маси за останнє століття. Навіть атомний стандарт, який використовується для визначення другого, може змінюватися через фізику поза нашими теперішніми знаннями. Зміна\(c\) може призвести до такої зміни, але будь-яка така зміна також може бути спричинена змінами інших фізичних констант, таких як інші, що відбуваються в постійній тонкій структурі. Такі питання більш детально розглядаються в розділі 9.6.
Обговорення питання\(\PageIndex{1}\)
Кулеметник в фігурці\(\PageIndex{15}\) розсилає бризки куль. Припустимо, що кулі стріляють в космічний простір, і що пройдені відстані складають трильйони миль (щоб людська фігура на схемі не масштабувалася). Після довгого часу кулі досягають точок, показаних крапками, які знаходяться однаково далеко від гармати. Їх прибуття в ці точки - це події\(A\) через\(E\), які відбуваються в різний час. Ланцюг ударів поширюється по всьому простору зі швидкістю, більшою ніж\(c\). Чи порушує це особливу відносність?

