1.5: Нерівності трикутника та Коші-Шварца
- Page ID
- 77329
Цілі навчання
- Обговоріть трикутник і Коші-Шварц
У евклідовій геометрії ми маємо інтуїтивно очевидний факт, що будь-яка сторона трикутника не більша за суму двох інших сторін. Це можна записати через вектори як\(|m + n| \leq |m| + |n|\). Тісно пов'язана з нею нерівність\(|m \cdot n| ≤ |m| |n|\), відома як нерівність Коші-Шварца, яку можна побачити тому\(m \cdot n = |m| |n| cos\theta\), що де\(\theta\) знаходиться кут між двома векторами.
Будь-яке доказ цих фактів в кінцевому рахунку залежить від припущення, що метрика має евклідовий підпис\(+ + +\) (або від еквівалентних припущень, таких як аксіоми Евкліда). Малюнок\(\PageIndex{1}\) показує, що за фізичними ознаками ми не очікуємо, що нерівності збережуться для векторів Мінковського в їх немодифікованих евклідових формах. Кількість |m + n| представляє належний час космічного корабля, який рухався інерційно разом із землею, в той\(|m| + |n|\) час як більший належний час переміщення космічного корабля.
З іншого боку, простір Мінковського має копії евклідового простору, побудовані в. Наприклад, ми знаємо, що всі знайомі евклідові факти повинні триматися в будь-якій площині одночасності, визначеної конкретним спостерігачем в даний момент часу, так як обмеження метрики до цієї площини має підпис\(---\), а відмінність між цим і\(+ + +\) підписом є довільним нотаційна конвенція. Підсумовуючи ці спостереження, ми очікуємо, що релятивістська версія трикутника і нерівностей Коші-Шварца буде розбита на випадки, деякі з яких такі ж, як у випадку Евкліда, а деякі з них різні.
Деякі нотаційні проблеми можуть бути заплутаними в наступному обговоренні. Ми дозволимо\(a^2\) означає\(a \cdot a\), що може бути не позитивним, а\(|a|\) вказує на позитивне дійсне число\(\mid a \cdot a\mid\). Я спробую конкретно вказати на будь-які рівняння, які вірні лише для\(+---\) підпису, а не для\(- + ++\), і висловити важливі кінцеві результати таким чином, який не залежить від цього вибору.
Два вектори, схожі на час
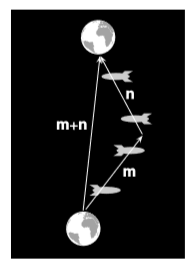
Простий і важливий випадок - це той випадок, в якому обидва\(m\) і\(n\) простежуються можливі світові лінії матеріальних об'єктів, як на малюнку\(\PageIndex{1}\). Тобто вони обидва повинні бути часовими векторами. Щоб побачити, яку форму має триматися нерівність Коші-Шварца, розбиваємо вектор\(n\) вниз на дві частини\(n = n_{\parallel} + n_{\perp}\), де\(n_{\parallel}\) паралельно\(m\) і\(n_{\perp}\) перпендикулярно. У нас тоді є\(|m · n| = |m · n_{\parallel} | = |m| |n_{\parallel} |\). Але\(n^2 = (n_{\parallel} + n_{perp} )^2 = n_{\parallel}^2 + 2n_{\parallel} \cdot n_{\perp} + n_{\perp} = n_{\parallel}^2 + n_{\perp}^2\), і так як\(n_{\parallel}\) це timeslike і\(n_{\perp}\) spaclike, у нас є (в\(+---\)\(n_{\parallel}^2 > 0\) підписі) і\(n_{\perp}^2 < 0\). Тому, незалежно від підпису\(\lvert n\lvert ≤ \lvert n_{\parallel}\lvert\), і ми маємо зворотну нерівність Коші-Шварца
\[|m \cdot n| \geq |m| |n| \quad \text{(valid for either + − −− or − + ++)}\]
Корисний спосіб інтерпретації розвороту порівняно з евклідовим випадком полягає в тому, що якщо вектори трапляються нормалізуватися таким чином\(|m| = |n| = 1\)\(m \cdot n = \gamma\), що, то де\(\gamma\) коефіцієнт Лоренца для спостерігача, чия світова лінія паралельна відносно світової лінії паралельно\(m\)\(n\) . Різниця від евклідової поведінки може бути зрозуміла як виникає з того факту, що тоді\(|cos\theta| ≤ 1\), коли ми завжди маємо\(\gamma \geq 1\).
Враховуючи фізичну мотивацію, представлену до цих пір, було б природно взяти обидва\(m\) і\(n\) лежати в майбутньому, а не в минулому світловому конусі, але ми ще не припускали, що це було так, і зворотна нерівність Коші-Шварца тримається незалежно від такого припущення. (Див. проблему Q16 для альтернативного способу побачити це.) Однак для того, щоб обговорити пов'язану нерівність трикутника, нам потрібно буде припустити, що обидва вектори спрямовані на майбутнє. Фізично це необхідно для того, щоб дати інтерпретацію, показану на малюнку ai, з якої ми вже зробили висновок, що нерівність трикутника повинна бути зворотна. Щоб перевірити це математично, ми можемо обчислити різницю\((m + n)^2 − (|m| + |n|)^2\) (задача 17).
Два просторові вектори, що не охоплюють світловий конус
Тепер припустимо, що\(m\) і обидва\(n\) космічні, і площина, яку вони охоплюють, не включає світловий конус. Діючи в межах цієї площини, ми ніколи не отримуємо ніяких часових або світлоподібних векторів, і тому неевклідова природа метрики нам ніколи не очевидна. Таким чином, геометрія цієї площини є евклідовою, тому в цьому випадку звичайні евклідові версії нерівностей Коші-Шварца та трикутника повинні триматися.
Приклад\(\PageIndex{1}\): No relativity required
Припустимо, що певний спостерігач встановлює Мінковський координати, і розглядає одиниці векторів\(\hat{x}\) і\(\hat{y}\) лежать уздовж\(y\) осей\(x\) і. \(x-y\)Площина, яку вони охоплюють, не включає світловий конус. Підключившись до координатної форми Мінковського метрики, ми виявляємо, що\(\hat{x} \cdot \hat{y} = 0\), як і очікувалося, оскільки геометрія\(x-y\) площини є евклідовою. Це задовольняє звичайну форму нерівності Коші-Шварца.
Два просторових вектори, що охоплюють світловий конус
Тепер розглянемо випадок, в координатах Мінковського, де\(m = (0, 5, 0, 0)\) і\(n = (4, 5, 0, 0)\). Ці вектори охоплюють\(t-x\) площину, геометрія якої не є евклідовою, і вони не задовольняють нерівності Евкліда Коші-Шварца, оскільки\(m \cdot n = -25\), тоді як\(|m| |n| = 15\). Два вектори цього типу завжди задовольнятимуть зворотній версії нерівності Коші-Шварца (задача Q18). Зворотний тримається в тому сенсі, що якщо два просторові вектори задовольняють сувору нерівність\(|m \cdot n| > |m| |n|\), то вони охоплюють світловий конус.
