1.4: Трансформація Лоренца

Last updated
Save as PDF

Page ID: 77316

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Вивчення трансформації Лоренца

Філософськи координати непотрібні, але вони зручні. Вони довільні, тому ми можемо переходити від одного набору до іншого. Наприклад, ми можемо змінити одиниці, що використовуються для вимірювання часу та положення, як у першій та другій панелям фігури\(\PageIndex{1}\). Нічого не змінюється щодо основних подій; лише мітки відрізняються. Третя панель показує зручну умовність, яку ми будемо використовувати для візуального зображення таких змін. Сірий прямокутник представляє вихідну сітку з першої панелі, а сітка чорних ліній представляє нову версію з другої панелі. Опущення сітки з сірого прямокутника полегшує візуальне декодування діаграми.

рис. 1.4.1.png — Малюнок\(\PageIndex{1}\): Дві події задаються як точки на графіку позиції та часу. Жанна д'Арк допомагає відновити Карла VII на престолі. У більш пізній час і на іншій посаді Жанна д'Арк засуджується до смертної кари.

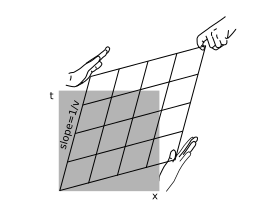
У спеціальній теорії відносності цікавить перетворення між координатами Мінковського спостерігачів, які перебувають у русі відносно один одного. Результат, показаний на малюнку\(\PageIndex{1}\), - це своєрідна розтяжка і згладжування діагоналей. Оскільки площа інваріантна, одна діагональ зростає на той самий коефіцієнт, за допомогою якого інша стискається. Ця зміна координат називається перетворенням Лоренца.

рис. 1.4.2.png — Малюнок\(\PageIndex{2}\): Перетворення Лоренца.

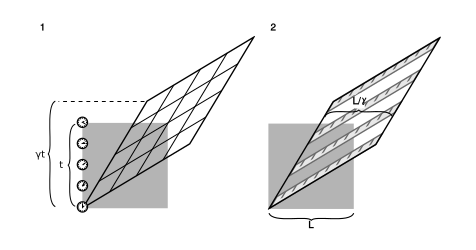
На малюнку\(\PageIndex{3}\) показано, як відбувається розширення часу та скорочення довжини на цій картині. Тут слід підкреслити, що перетворення Лоренца включає більше ефектів, ніж просто скорочення довжини та розширення часу. Багато новачків у відносності плутаються і приходять до помилкових висновків, намагаючись звести все до питання вставки коефіцієнтів\(\gamma\) в різні рівняння. Якби перетворення Лоренца склало не що інше, як скорочення довжини та розширення часу, це була б просто зміна одиниць, як та, що показана на малюнку\(\PageIndex{1}\).

рис. 1.4.3.png — Малюнок\(\PageIndex{3}\): на малюнку показано, як відбувається розширення часу та скорочення довжини на цій картині. Тут слід підкреслити, що перетворення Лоренца включає більше ефектів, ніж просто скорочення довжини.

Перетворення Лоренца можна позначити алгебраїчно:

\[t' = \gamma t - \nu\gamma x \\ x' = -\nu\gamma t + \gamma x \label{\(\PageIndex{1}\)}\]

Те, що це правильна релятивістська трансформація, можна переконатися, зазначивши, що

\(x = \pm t\)збережені лінії швидкості світла, і
детермінант дорівнює\(1\).

щоб площі збереглися. Як варіант, достатньо перевірити інваріантність просторово-часового інтервалу при цьому перетворенні.

Рівняння\(\PageIndex{1}\) обробляють простір і час ідеально симетрично, але це не слід сприймати як те, що має на увазі, що особлива відносність прекрасно втілює таку симетрію. Наприклад, я можу легко переглянути місце, в якому я був раніше, але я не можу повернутися назад у часі. І звичайно, ми маємо три виміри простору; наше використання\(1+1\) розмірів,\(3+1\) а не просто питання зручності на даний момент. Зауважте також, що немає точної аналогії між малюнком\(\PageIndex{3}\) (1), де годинник є точковим об'єктом, що трасує лінію через просторовий час, і фігурою\(\PageIndex{3}\) (2), де лінійка є розширене тіло, яке змітає паралельну стрічку.

Приклад\(\PageIndex{1}\): Observers agree on their relative speeds

Спостерігач\(A\) каже,\(B\) що спостерігач віддаляється від неї зі швидкістю\(v\); чи правда, як у галілейській відносності, що\(B\) вимірює ту саму швидкість для\(A\)?

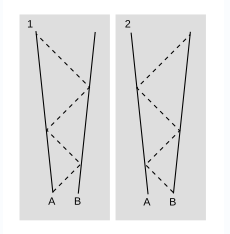
рис. 1.4.4.png — Малюнок\(\PageIndex{4}\): Спостерігачі та їх відносні швидкості

Так, це правда, але не зовсім очевидно. Один із способів перевірити цей факт - перевірити, чи перетворення Лоренца зі швидкостями\(v\) і\(-v\) є зворотними. Більш фізично прозоре обгрунтування показано на малюнку\(\PageIndex{4}\). На малюнку\(\PageIndex{4}\) (1)\(A\) визначає\(B’s\) швидкість відносно неї, посилаючи два зворотні сигнали зі швидкістю світла, і вимірюючи різницю між двома краями в обидва кінці. Оскільки простір однаковий у всіх напрямках, експериментальні дані абсолютно однакові, коли\(B\) проводиться вимірювання, цифра\(\PageIndex{4}\) (2), і тому\(B\) виводить однакову швидкість.

Приклад\(\PageIndex{2}\): Motion in the opposite direction

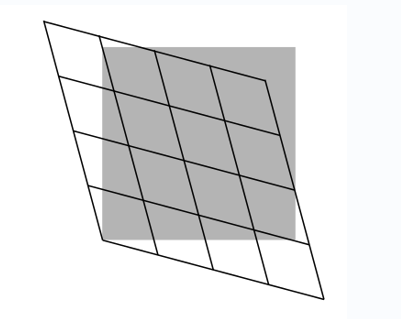
\(\PageIndex{5}\)На малюнку показаний випадок, коли спостерігач, кадр якого представлений сіткою, рухається вліво щодо того, чий кадр представлений сірим квадратом.

рис. 1.4.5.png — Малюнок\(\PageIndex{5}\): Рух у зворотному напрямку

Приклад\(\PageIndex{3}\): Other quadrants

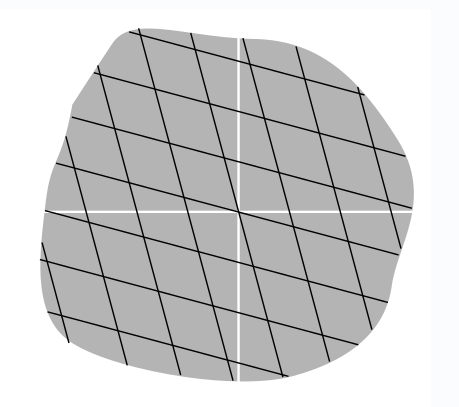
рис. 1.4.6.png — Малюнок\(\PageIndex{6}\): Інші квадранти

До цих пір я довільно вибирав, щоб намалювати тільки перший quad- рант кожної системи координат. \(\PageIndex{6}\)На малюнку показана область, яка включає всі чотири квадранти.

Приклад\(\PageIndex{4}\): A numerical example of invariance

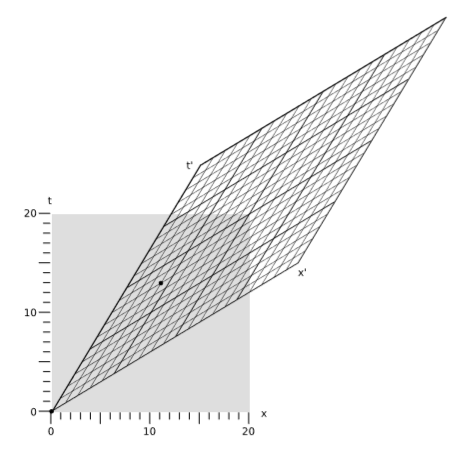
\(\PageIndex{7}\)На малюнку показані дві системи відліку в русі відносно один одного в\(v = \frac{3}{5}\). (Для цієї швидкості розтягування і розгойдування основних діагоналей обидва в рази\(2\)). Події позначені за координатами, які в кадрі, представленому квадратом, знаходяться

\[(t,x) = (0,0) \\ (t,x) = (13,11)\]

Інтервал між цими подіями становить\(13^2 - 11^2 = 48\). У кадрі, представленому паралелограмом, за координатами лежать ті ж дві події.

\[(t',x') = (0,0) \\ (t',x') = (8,4)\]

Розраховуючи інтервал за допомогою цих значень\(8^2 - 4^2 = 48\), виходить результат, який виходить таким же, як і в іншому кадрі.

рис. 1.4.7.png — Малюнок\(\PageIndex{7}\): Дві системи відліку в русі відносно один одного

Приклад\(\PageIndex{5}\): The garage paradox

Один з найвідоміших з усіх так званих парадоксів відносності пов'язаний з нашим неправильним почуттям, що одночасність чітко визначена. Ідея полягає в тому, що можна було б взяти шкільний автобус і загнати його на релятивістських швидкостях в гараж звичайного розміру, в який він нормально не помістився б. Через скорочення довжини автобус нібито поміститься в гаражі. Водій, однак, сприйматиме гараж як контракт і, таким чином, ще менш здатний утримувати автобус.

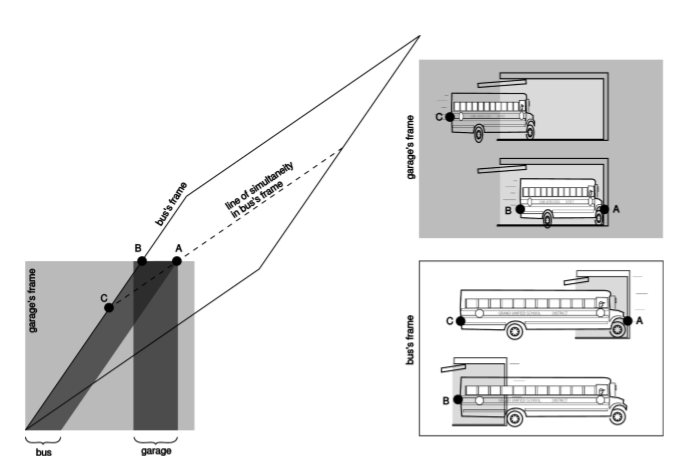
рис. 1.4.8.png — Малюнок\(\PageIndex{8}\): У рамці відліку гаража шина рухається, і може поміститися в гаражі за рахунок скорочення його довжини. У системі відліку автобуса гараж рухається, і не може утримувати автобус через його скорочення довжини.

Парадокс вирішується, коли ми визнаємо, що концепція примірки автобуса в гаражі «все відразу» містить приховане припущення, припущення, що має сенс запитати, чи може передня і задня частина автобуса одночасно перебувати в гаражі. Спостерігачі в різних системах відліку, що рухаються з високою відносною швидкістю, не обов'язково погоджуються, чи відбуваються речі одночасно. Як показано на малюнку ав. людина в рамі гаража може закрити двері в одну мить Б, він сприймає як одночасне з приходом переднього бампера А на задню стінку гаража, але водій не погодиться про одночасність цих двох подій, і сприймав би двері як зачинені довго. після того, як вона переорана через задню стінку.

Приклад\(\PageIndex{6}\): Shifting clocks

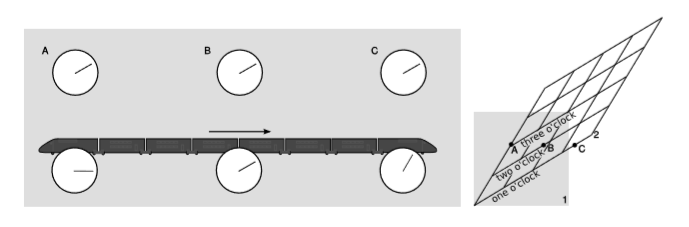
рис. 1.4.9.png — Малюнок\(\PageIndex{9}\): Переміщення годинника

Верхній ряд годин на малюнку\(\PageIndex{9}\) розташовані в трьох різних місцях. Вони були синхронізовані в системі відліку землі, представленої папером. Ця синхронізація здійснюється шляхом обміну світловими сигналами (синхронізація Ейнштейна). Наприклад, якщо передній і задній годинник надсилають спалахи світла, коли вони думають, що це\(2\) година, той, що посередині, отримає їх обидва одночасно. Подія\(A\) - це та, при якій задній годинник\(A\) читає\(2\) годину тощо.

Нижній ряд годин знаходяться на борту поїзда, і були синхронізовані аналогічним чином. З причин, розглянутих у прикладі 1.1.4 у розділі 1.1, їх синхронізація відрізняється від синхронізації наземних годинників. Посилаючись на діаграму перетворення Лоренца, показану праворуч, ми бачимо, що в кадрі поїзда\(2\),\(C\) відбувається спочатку, потім\(B\), потім\(A\).

Це приклад тлумачення терміна\(t' = \dots - \nu\gamma x\) в трансформації Лоренца (ур. \(\PageIndex{1}\)). Оскільки події відбуваються по-різному\(x’s\), кожен зміщується в часі щодо наступного, відповідно до годинників, синхронізованих в кадрі 2 (\(t'\), поїзд).

Приклад\(\PageIndex{7}\): Deja vu?

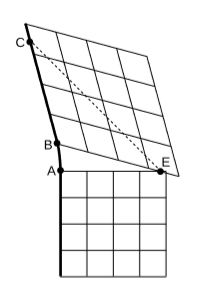
рис. 1.4.10.png — Малюнок\(\PageIndex{10}\): Дежавю

Сітки, які ми малювали, - це прості умовності, такі ж складні та довільні, як плаття в дворі Людовика XIV. Вони походять від геодезичного процесу, який, можливо, доведеться планувати заздалегідь і результати якого ми, можливо, не зможемо побачити пізніше. Темна лінія на малюнку\(\PageIndex{10}\) - це світова лінія спостерігача\(O\), який деякий час рухається інерційно, розганяється вліво, а потім знову рухається інерційно. Праворуч наклеєні дві координатні сітки, адаптовані до двох інерційних відрізків. На заході\(E\) Буш краде вибори 2000 року, і це зображено як одночасне як з подією, так\(A\) і з подією\(B\). Чи бідний О бачить, що це трапляється двічі? Ні, навіть якщо погані новини передаються сигналом, що рухається зі швидкістю світла (пунктирною лінією),\(O\) отримує його тільки один раз, на подію\(C\).

Єдина проблема тут - поганий вибір етикеток, що призводить\(E\) до того, що вони мають більше однієї етикетки. Щось подібне відбувається в кадрі постійного прискорення, розділ 7.1,

Багато помилок початківців у відносності обертаються навколо набору нерозглянутих упереджень про те, що означає спостерігати за речами. Один уявляє, що такі ефекти, як скорочення довжини та розширення часу, - це те, що насправді бачить спостерігач, і, можливо, цей процес бачення миттєвий. Або хтось думає про координати Мінковського так, ніби вони були результатом простого і автоматичного процесу сприйняття спостерігачем. Це таке мислення, яке змусить повірити,\(\PageIndex{7}\) що приклад божевільний або парадоксальний.

рис. 1.4.11.png — Малюнок\(\PageIndex{11}\): Координати Мінковського є результатом складного процесу геодезії.

Як інший приклад, не слід уявляти, що скорочення довжини палиці\(\frac{1}{\gamma}\) - це те, що насправді бачить спостерігач, дивлячись на палицю. На оптичні спостереження впливають, наприклад, нерівні часи, прийняті для поширення світла від кінців палиці до ока. Моделювання цього типу ефекту намальовано в прикладі 1.3.3.

Скорочення довжини, розширення часу, залежність від одночасності спостерігача та координати Мінковського - все це складні результати трудомісткого процесу збору та аналізу даних, отриманих такими методами, як синхронізація Ейнштейна, які вимагають таких дій, як консультація атомних годин або обмін сигнали між різними точками зі швидкістю світла. Малюнок\(\PageIndex{11}\) окреслює такий процес мультяшним способом. Флот ракетних кораблів, що перевозять геодезистів, відправляється з Землі і розкинувся по великій області космосу. Геодезисти дивляться через свої теодоліти на зображення, які утворюються світловими променями (пунктирними лініями), що надійшли після подорожі з кінцевою швидкістю c Такі світлові промені несуть стару, несвіжу інформацію про різні події. Вибухнула ядерна війна. Рок-н-рольна музика прибула на Сатурн. Отримані дані потім передаються різними способами (пасажирський голуб, кодоване Морсом радіо, паперова пошта) і консолідуються в геодезичному бюро. В офісі працівники за довгим рядом парт хрумтять цифри і виробляють діаграму координат Мінковського з подіями, позначеними в.