1.4: замовлена геометрія

Last updated
Save as PDF

Page ID: 77671

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Давайте спробуємо помістити те, що ми дізналися, в загальний геометричний контекст.

Знайома Евкліда геометрія двовимірного простору має наступні аксіоми, ⁶ які виражаються в терміні операцій, які можуть бути здійснені за допомогою компаса і немаркованого прямокутника:

E1 Дві точки визначають лінію.
Відрізки лінії E2 можуть бути розширені.
E3 Унікальне коло може бути побудовано з урахуванням будь-якої точки як його центру і будь-якого відрізка лінії як його радіус.
E4 Всі прямі кути рівні один одному.
E5 Паралельний постулат: З огляду на лінію і точку, яка не знаходиться на лінії, через точку можна провести не більше однієї лінії і паралельно заданій лінії. ⁷

Примітка

Це форма, відома як аксіома Playfair, а не версія постулату, спочатку надана Евклідом.

Сучасний стиль в математиці полягає в тому, щоб розглядати цей тип аксіоматичної системи як самодостатню пісочницю, з аксіомами, і будь-якими теоремами, доведеними з них, будучи істинними чи хибними лише по відношенню один до одного. Евклід і його сучасники, однак, вважали їх емпіричними фактами про фізичну реальність. Наприклад, п'ятий постулат вони вважали менш очевидним, ніж перші чотири, тому що для того, щоб фізично переконатися, що дві лінії паралельні, теоретично доведеться продовжити їх на нескінченну відстань і переконатися, що вони ніколи не перетинаються. У перших 28 теоремах про Стихії Евклід повністю обмежується пропозиціями, які можна довести, грунтуючись на більш безпечних перших чотирьох постулатах. Більш загальна геометрія, визначена пропуском паралельного постулату, відома як абсолютна геометрія.

Яка геометрія, ймовірно, може бути застосована до загальної теорії відносності? Ми відразу бачимо, що евклідова геометрія, або навіть абсолютна геометрія, була б занадто спеціалізованою. Ми маємо на увазі опис подій, які є точками як в просторі, так і в часі. Обмежуючись для легкості візуалізації одним виміром вартістю простору, ми, безумовно, можемо побудувати площину, описану координатами (t, x), але накладення постулатів Евкліда на цю площину призводить до фізичної нісенітниці. Простір і час фізично відрізняються один від одного. Але постулати 3 і 4 описують геометрію, в якій відстані, виміряні по непаралельних осях, можна порівняти, і фігури можуть вільно обертатися, не впливаючи на істинність або неправдивість висловлювань про них; це підходить лише для фізичного опису різних космічних напрямків, як у (x, y) площині, дві осі якої не відрізняються.

Нам потрібно викинути за борт більшу частину спеціалізованого апарату евклідової геометрії. Після того, як ми позбавили нашу геометрію до мінімуму, ми можемо повернутися назад і створити інший набір обладнання, яке буде краще підходить для відносності.

Урізана геометрія, яку ми хочемо, називається впорядкованою геометрією, і була розроблена Моріцем Пашем приблизно в 1882 році. Як припускає притча про Алісу і Бетті, впорядкована геометрія не має жодної глобальної, всеохоплюючої системи вимірювання. Коли Бетті відправляється в свою подорож, вона простежує певний шлях через простір подій, а Аліса, залишаючись вдома, простежує інший. Незважаючи на те, що події відбуваються в причинно-наслідковому порядку уздовж кожного з цих шляхів, ми не очікуємо, що зможемо виміряти час уздовж шляхів A і B, і вони вийдуть однаковими. Так працює впорядкована геометрія: точки можна ставити в певному порядку уздовж будь-якої конкретної лінії, але не по різних лініях. З чотирьох примітивних понять, що використовуються в E1-E5 Евкліда — точка, лінія, коло та кут — у впорядкованій геометрії актуальні лише неметричні поняття точки (тобто події) та прямої. У геометрії без вимірювання немає поняття вимірювання відстані (отже, немає циркулів або кіл) або вимірювання кутів. Позначення [ABC] вказує на те, що подія B лежить на відрізку лінії, що з'єднує A і C, і знаходиться строго між ними.

Аксіоми впорядкованої геометрії такі: ⁸

O1 Дві події визначають лінію.
Відрізки лінії O2 можуть бути розширені: задані A і B, є принаймні одна подія така, що [ABC] є істинним.
Лінії O3 не обертаються навколо: якщо [ABC] вірно, то [BCA] є помилковим.
O4 Міжостість: Для будь-яких трьох різних подій A, B та C, що лежать на одній лінії, ми можемо визначити, чи знаходиться B між A та C (і за твердженням 3 цей порядок є унікальним, за винятком можливого загального розвороту для формування [CBA]).

Примітка

Малюнок 1.4.1.png — Малюнок 1.4.1 - Аксіоми О2 (зліва) і О3 (праворуч).

Аксіоми узагальнені для зручного ознайомлення. Це має бути неформальний, читабельний підсумок системи, підібраний до того ж рівня нещільності, що і E1-E5 Евкліда. Сучасні математики виявили, що такі системи насправді потребують трохи більше технічних механізмів, щоб бути абсолютно суворими, тому, якщо ви подивитеся на аксіоматизацію впорядкованої геометрії або сучасну аксіоматизацію евклідової геометрії, ви, як правило, знайдете набагато більш довгий список аксіом, ніж ті. представлений тут. Аксіоми, які я опускаю, піклуються про такі деталі, як переконатися, що у Всесвіті є більше двох точок, і що криві не можуть прорізати один одного, не перетинаючись. Класична, красиво написана книга на ці теми є H.S.M. Coxeter's Вступ до геометрії, який є «вступним» в тому сенсі, що це така книга, яку математика коледжу може використовувати в першому курсі верхнього дивізіону в геометрії.

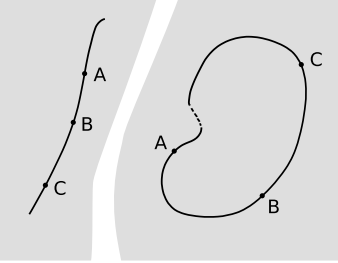
O1-O2 висловлюють ті ж ідеї, що і E1-E2 Евкліда. Не всі лінії в системі будуть фізично відповідати ланцюгам причинно-наслідкового зв'язку; ми могли б мати відрізок лінії, який описує знімок сталевого ланцюга, а O3-O4 потім сказати, що порядок ланок чітко визначено. Але O3 і O4 також мають чітке фізичне значення для ліній, що описують причинно-наслідковий зв'язок. O3 забороняє парадокси подорожей у часі, як повернення у часі та вбивство нашої власної бабусі в дитинстві; Цифра вище ілюструє, чому порушення O3 називають закритою кривою, схожою на час. O4 каже, що події гарантовано матимуть чітко визначений причинно-наслідковий порядок, лише якщо вони лежать на одній лінії. Це зовсім відрізняється від ставлення, вираженого в знаменитому висловлюванні Ньютона: «Абсолютне, істинне і математичне час, само по собі, і від власної природи тече однаково без урахування нічого зовнішнього...»

Якщо ви стурбовані жорсткою економією системи геометрії без будь-якого поняття вимірювання, ви можете бути більш злякані, дізнавшись, що навіть така слабка система, як впорядкована геометрія, робить деякі твердження, які є занадто сильними, щоб бути повністю правильними як основа відносності. Наприклад, якщо спостерігач потрапить в чорну діру, то в якийсь момент він досягне центральної точки нескінченної щільності, званої сингулярністю. У цей момент його причинно-наслідковий ланцюг припиняється, порушуючи\ O2). Це також відкрите питання, чи насправді заборона O3 на часові петлі має загальну відносність; це грайливо названа гіпотеза захисту хронології Стівена Хокінга. Ми також побачимо, що в цілому відносність O1 майже завжди вірна, але є винятки.

Малюнок 1.4.2.png — Малюнок 1.4.2 - Стівен Хокінг (1942-).