1.24: Молекулярні вібрації
- Page ID
- 17560
Коливальний рух у двоатомних молекулах часто обговорюється в контексті простого гармонічного осцилятора в квантовій механіці. Двоатомна молекула має лише єдиний зв'язок, який може вібрувати; ми говоримо, що вона має єдиний вібраційний режим. Як ви могли очікувати, коливальні рухи багатоатомних молекул набагато складніші, ніж ті, що знаходяться в двоатомних. По-перше, є більше зв'язків, які можуть вібрувати; а по-друге, крім коливань розтягування, єдиного типу вібрації, можливого в двоатомному, ми також можемо мати згинальні і крутильні коливальні режими. Оскільки зміна однієї довжини зв'язку в багатоатомній часто впливає на довжину сусідніх зв'язків, ми не можемо розглядати коливальний рух кожного зв'язку в ізоляції; натомість ми говоримо про нормальні режими, що включають узгоджений рух груп зв'язків. Як простий приклад, нормальні режими лінійної триатомної молекули наведені нижче.

Як тільки ми дізнаємося симетрію молекули за її рівноважною структурою, теорія груп дозволяє нам передбачити коливальні рухи, які вона зазнає, використовуючи точно ті самі інструменти, які ми використовували вище для дослідження молекулярних орбіталів. Кожен коливальний режим перетворюється як одне з нескорочуваних уявлень точкової групи молекули. Перш ніж перейти до прикладу, ми швидко розглянемо, як визначити кількість коливальних режимів в молекулі.
Молекулярні ступені свободи — визначення кількості нормальних коливальних режимів
Атом може зазнавати тільки поступальний рух, і тому має три ступені свободи, відповідні руху вздовж\(x\), \(y\), and \(z\) Cartesian axes. Translational motion in any arbitrary direction can always be expressed in terms of components along these three axes. When atoms combine to form molecules, each atom still has three degrees of freedom, so the molecule as a whole has \(3N\) degrees of freedom, where \(N\) is the number of atoms in the molecule. However, the fact that each atom in a molecule is bonded to one or more neighboring atoms severely hinders its translational motion, and also ties its motion to that of the atoms to which it is attached. For these reasons, while it is entirely possible to describe molecular motions in terms of the translational motions of individual atoms (we will come back to this in the next section), we are often more interested in the motions of the molecule as a whole. These may be divided into three types: translational; rotational and vibrational.
Так само, як і для окремого атома, молекула в цілому має три ступені поступальної свободи, залишаючи\(3N - 3\) degrees of freedom in rotation and vibration.
Кількість обертальних ступенів свободи залежить від будови молекули. Загалом, існує три можливі обертальні ступені свободи, що відповідають обертанню про\(x\), \(y\), and \(z\) Cartesian axes. A non-linear polyatomic molecule does indeed have three rotational degrees of freedom, leaving \(3N - 6\) degrees of freedom in vibration (i.e \(3N - 6\) vibrational modes). In a linear molecule, the situation is a little different. It is generally accepted that to be classified as a true rotation, a motion must change the position of one or more of the atoms. If we define the \(z\) axis as the molecular axis, we see that spinning the molecule about the axis does not move any of the atoms from their original position, so this motion is not truly a rotation. Consequently, a linear molecule has only two degrees of rotational freedom, corresponding to rotations about the \(x\) and \(y\) axis. This type of molecule has \(3N - 5\) degrees of freedom left for vibration, or \(3N - 5\) vibrational modes.
Підсумовуючи:
- Лінійна молекула має\(3N - 5\) vibrational modes
- Нелінійна молекула має\(3N - 6\) vibrational modes.
Визначення симетрії молекулярних рухів
Вище ми згадували, що процедура визначення нормальних коливальних мод багатоатомної молекули дуже схожа на ту, яка використовувалася в попередніх розділах для побудови молекулярних орбіталей. Насправді, практично єдиною відмінністю між цими двома додатками теорії груп є вибір базової множини.
Як ми вже встановили, рухи молекули можуть бути описані з точки зору рухів кожного атома вздовж\(x\), \(y\) and \(z\) axis. Consequently, it probably won’t come as too much of a surprise to discover that a very useful basis for describing molecular motions comprises a set of \(\begin{pmatrix} x, y, z \end{pmatrix}\) axes centered on each atom. This basis is usually known as the \(\textit{3N}\) Cartesian basis (since there are \(3N\) Cartesian axes, \(3\) axes for each of the \(N\) atoms in the molecule). Note that each molecule will have a different \(3N\) Cartesian basis, just as every molecule has a different atomic orbital basis.
Нашим першим завданням при дослідженні рухів конкретної молекули є визначення символів матричних представників для\(3N\) Cartesian basis under each of the symmetry operations in the molecular point group. We will use the \(H_2O\) molecule, which has \(C_{2v}\) symmetry, as an example.
\(H_2O\) has three atoms, so the \(3N\) Cartesian basis will have \(9\) elements. The basis vectors are shown in the diagram below.
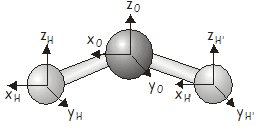
Одним із способів визначення символів було б побудувати всі представники матриці та взяти їх сліди. Хоча ви можете спробувати цей підхід, якщо ви хочете отримати певну практику в побудові представників матриці, є простіший спосіб. Нагадаємо, що ми також можемо визначити характер представника матриці під певною операцією симетрії, пройшовши базисні функції і застосувавши такі правила:
- Додайте\(1\) до символу, якщо базова функція незмінна операцією симетрії;
- Додати\(-1\) до символу, якщо базисна функція змінює знак під операцією симетрії;
- Додайте\(0\) до символу, якщо базова функція рухається при застосуванні операції симетрії.
Для\(H_2O\), this gives us the following characters for the \(3N\) Cartesian basis (check that you can obtain this result using the rules above and the basis vectors as drawn in the figure):
\[\begin{array}{lcccc} \text{Operation:} & E & C_2 & \sigma_v(xz) & \sigma_v'(yz) \\ \chi_{3N}: & 9 & -1 & 3 & 1 \end{array} \tag{24.1}\]
Є ще більш швидкий спосіб опрацювати персонажів\(3N\) Cartesian basis if you have a character table in front of you. The character for the Cartesian basis is simply the sum of the characters for the \(x\), \(y\), and \(z\) (or \(T_x\), \(T_y\), and \(T_z\)) functions listed in the character table. To get the character for the \(\textit{3N}\) Cartesian basis, simply multiply this by the number of atoms in the molecule that are unshifted by the symmetry operation.
The\(C_{2v}\) character table is shown below.
\[\begin{array}{l|cccc|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & h = 4 \\ \hline A_1 & 1 & 1 & 1 & 1 & z, x^2, y^2, z^2 \\ A_2 & 1 & 1 & -1 & -1 & xy, R_z \\ B_1 & 1 & -1 & 1 & -1 & x, xz, R_y \\ B_2 & 1 & -1 & -1 & 1 & y, yz, R_x \\ \hline \end{array} \tag{24.2}\]
\(x\) transforms as \(B_1\), \(y\) as \(B_2\), and \(z\) as \(A_1\), so the characters for the Cartesian basis are
\[\begin{array}{lcccc} \text{Operation:} & E & C_2 & \sigma_v(xz) & \sigma_v'(yz) \\ \chi_{3N}: & 3 & -1 & 1 & 1 \end{array} \tag{24.3}\]
Ми множимо кожен з них на кількість незміщених атомів (\(3\) for the identity operation, \(1\) for \(C_2\), \(3\) for \(\sigma_v\) і\(1\) for \(\sigma_v'\)), щоб отримати символи для\(3N\) Cartesian basis.
\[\begin{array}{lcccc} \chi_{3N}: & 9 & -1 & 3 & 1 \end{array} \tag{24.4}\]
Заспокійливо, ми отримуємо ті ж символи, що і раніше. Який з трьох методів ви використовуєте, щоб дістатися до цього моменту - вирішувати вам.
Тепер у нас є символи для молекулярних рухів (описаних в\(3N\) Cartesian basis) under each symmetry operation. At this point, we want to separate these characters into contributions from translation, rotation, and vibration. This turns out to be a very straightforward task. We can read the characters for the translational and rotational modes directly from the character table, and we obtain the characters for the vibrations simply by subtracting these from the \(3N\) Cartesian characters we’ve just determined. The characters for the translations are the same as those for \(\chi_{Cart}\). Знаходимо символи для обертань, складаючи разом символи для\(R_x\), \(R_y\), and \(R_z\) from the character table (or just \(R_x\) and \(R_y\) if the molecule is linear). For \(H_2O\), we have:
\[\begin{array}{lcccc} \text{Operation:} & E & C_2 & \sigma_v(xz) & \sigma_v'(yz) \\ \chi_{3N}: & 9 & -1 & 3 & 1 \\ \chi_{\text{Trans}}: & 3 & -1 & 1 & 1 \\ \chi_{\text{Rot}}: & 3 & -1 & -1 & -1 \\ \chi_{\text{Vib}} = \chi_{3N} - \chi_{\text{Trans}} - \chi_{\text{Rot}}: & 3 & 1 & 3 & 1 \end{array} \tag{24.5}\]
Символи в останньому рядку - це суми символів для всіх молекулярних коливань. Ми можемо дізнатися симетрії окремих коливань, використовуючи рівняння зменшення (Рівняння (15.20)) для визначення внеску з кожного незвідного подання.
У багатьох випадках вам навіть не потрібно буде використовувати рівняння, і ви можете з'ясувати, які нескорочувані уявлення сприяють лише оглядом таблиці символів. У даному випадку єдиною комбінацією нескорочуваних уявлень, здатних дати необхідні значення для\(\chi_{\text{Vib}}\) є\(2A_1 + B_1\). As an exercise, you should make sure you are also able to obtain this result using the reduction equation.
Поки що все це може здатися трохи абстрактним, і ви, мабуть, хочете знати, що таке вібрації\(H_2O\) actually look like. For a molecule with only three atoms, it is fairly easy to identify the possible vibrational modes and to assign them to the appropriate irreducible representation.
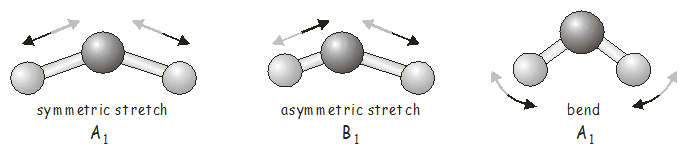
Для більшої молекули проблема може стати набагато складнішою, і в цьому випадку ми можемо генерувати SALC\(3N\) Cartesian basis, which will tell us the atomic displacements associated with each vibrational mode. We will do this now for \(H_2O\).
Атомні переміщення з використанням декартової основи 3N
Як і раніше, ми генеруємо SALC кожної симетрії шляхом застосування відповідного оператора проекції до кожної з базисних функцій (або в даному випадку базисних векторів)\(f_i\) in turn.
\[\phi_i = \sum_g \chi_k(g) g f_i \tag{24.6}\]
У цьому випадку ми маємо\(9\) basis vectors, which we will label \(x_H\), \(y_H\), \(z_H\), \(x_O\), \(y_O\), \(z_O\), \(x_{H'}\), \(y_{H'}\), \(z_{H'}\), describing the displacements of the two \(H\) atoms and the \(O\) atom along Cartesian axes. For the SALCs of \(A_1\) symmetry, applying the projection operator to each basis vector in turn gives (check that you can obtain this result):
\[\begin{array}{rclll} \phi_1(x_H) & = & x_H - x_{H'} + x_H - x_{H'} & = & 2x_H - 2x_{H'} \\ \phi_2(y_H) & = & y_H - y_{H'} - y_H + y_{H'} & = & 0 \\ \phi_3(z_H) & = & z_H + z_{H'} + z_H + z_{H'} & = & 2z_H + 2z_{H'} \\ \phi_4(x_O) & = & x_O - x_O + x_O - x_O & = & 0 \\ \phi_5(y_O) & = & y_O - y_O - y_O + y_O & = & 0 \\ \phi_6(z_O) & = & z_O + z_O + z_O + z_O & = & 4z_O \\ \phi_7(x_{H'}) & = & x_{H'} - x_H + x_{H'} - x_H & = & 2x_{H'} - 2x_H \\ \phi_8(y_{H'}) & = & y_{H'} - y_H - y_{H'} + y_H & = & 0 \\ \phi_9(z_{H'}) & = & z_{H'} + z_H + z_{H'} + z_H & = & 2z_{H'} + 2z_H \end{array} \tag{24.7}\]
Ми бачимо, що рух, характерний для\(A_1\) vibration (which we have identified as the symmetric stretch and the bending vibration) may be summarized as follows:
- \(2(x_H - x_{H'})\)- два атома водню рухаються в протилежних напрямках уздовж\(x\) осі.
- \(2(z_H + z_{H'})\)- два атома водню рухаються в одному напрямку вздовж\(z\) осі.
- \(4z_O\)- атом кисню рухається уздовж\(z\) осі.
- Немає руху жодного з атомів у\(y\) напрямку.
Асиметрична стрейч має\(B_1\) symmetry, and applying the projection operator in this case gives:
\[\begin{array}{rclll} \phi_1(x_H) & = & x_H + x_{H'} + x_H + x_{H'} & = & 2x_H + 2x_{H'} \\ \phi_2(y_H) & = & y_H + y_{H'} - y_H - y_{H'} & = & 0 \\ \phi_3(z_H) & = & z_H - z_{H'} + z_H - z_{H'} & = & 2z_H - 2z_{H'} \\ \phi_4(x_O) & = & x_O + x_O + x_O + x_O & = & 4x_O \\ \phi_5(y_O) & = & y_O + y_O - y_O - y_O & = & 0 \\ \phi_6(z_O) & = & z_O - z_O + z_O - z_O & = & 0 \\ \phi_7(x_{H'}) & = & x_{H'} + x_H + x_{H'} + x_H & = & 2x_{H'} + 2x_H \\ \phi_8(y_{H'}) & = & y_{H'} + y_H - y_{H'} - y_H & = & 0 \\ \phi_(z_{H'}) & = & z_{H'} - z_H + z_{H'} - z_H & = & 2z_{H'} - 2z_H \end{array} \tag{24.8}\]
У цьому коливальному режимі два\(H\) atoms move in the same direction along the \(x\) axis and in opposite directions along the \(z\) axis.
Зараз ми показали, як теорія груп може бути використана разом з\(3N\) Cartesian basis to identify the symmetries of the translational, rotational and vibrational modes of motion of a molecule, and also to determine the atomic displacements associated with each vibrational mode.
Молекулярні коливання з використанням внутрішніх координат
Хоча було досить просто досліджувати атомні переміщення, пов'язані з кожним коливальним режимом\(H_2O\) using the \(3N\) Cartesian basis, this procedure becomes more complicated for larger molecules. Also, we are often more interested in how bond lengths and angles change in a vibration, rather than in the Cartesian displacements of the individual atoms. If we are only interested in looking at molecular vibrations, we can use a different procedure from that described above, and start from a basis of internal coordinates. Internal coordinates are simply a set of bond lengths and bond angles, which we can use as a basis for generating representations and, eventually, SALCs. Since bond lengths and angles do not change during translational or rotational motion, no information will be obtained on these types of motion.
Для\(H_2O\), the three internal coordinates of interest are the two \(OH\) bond lengths, which we will label \(r\) and \(r'\), and the \(HOH\) bond angle, which we will label \(\theta\) . Якби ми хотіли, ми могли б розділити нашу основу на дві різні основи, одну, що складається лише з довжин зв'язків, щоб описати вібрації розтягування, і одну, що складається лише з кутів зв'язку, щоб описати вібрації згинання. Однак нинішній приклад досить простий, щоб розглядати всі основні функції разом.
Як завжди, нашим першим кроком є опрацювання символів представників матриці для цієї основи під кожну операцію симетрії. Наслідки різних перетворень на обраній нами основі та характери відповідних представників:
\[\begin{array}{lc} E(r, r', \theta) = (r, r', \theta) & \chi(E) = 3 \\ C_2(r, r', \theta) = (r', r, \theta) & \chi(C_2) = 1 \\ \sigma_v(xz)(r, r', \theta) = (r, r', \theta) & \chi(\sigma_v) = 3 \\ \sigma_v'(yz)(r, r', \theta) = (r', r, \theta) & \chi(\sigma_v') = 1 \end{array} \tag{24.9}\]
Це ті ж символи, що ми знайшли перед використанням\(3N\) Cartesian basis, and as before, we can see by inspection of the character table that the representation may be reduced down to the sum of irreducible representations \(2A_1 + B_1\). We can now work out the symmetry adapted linear combinations of our new basis set to see how the bond lengths and angle change as \(H_2O\) vibrates in each of the three vibrational modes.
Знову ж таки, ми будемо використовувати оператор проекції,\(\phi_i = \Sigma_g \chi_k(g) g f_i\) застосований до кожної базової функції по черзі.
По-перше,\(A_1\) vibrations:
\[\begin{array}{rclll} \phi_1(r) & = & r + r' + r + r' & = & 2(r + r') \\ \phi_2(r') & = & r' + r + r' + r & = & 2(r' + r) \\ \phi_3(\theta) & = & \theta + \theta + \theta + \theta & = & 4\theta \end{array} \tag{24.10}\]
З цих SALC ми можемо ідентифікувати\(\phi_1\) (і\(\phi_2\), що ідентично) з симетричним розтягуванням, при якому обидві довжини зв'язку змінюються по фазі один з одним, і\(\phi_3\) з вигином.
Тепер для\(B_1\) vibration:
\[\begin{array}{rclll} \phi_4(r) & = & r - r' + r - r' & = & 2(r - r') \\ \phi_5(r') & = & r' - r + r' - r & = & 2(r' - r) \\ \phi_6(\theta) & = & \theta - \theta + \theta - \theta & = & 0 \end{array} \tag{24.11}\]
\(\phi_4\) and \(\phi_5\)не є лінійно незалежними, і будь-який з них може бути обраний для опису асиметричної розтяжки, при якій одна зв'язок подовжується, а інша вкорочується.
Примітка: При використанні внутрішніх координат важливо, щоб всі координати в основі були лінійно незалежними. Якщо це так, то кількість внутрішніх координат в основі буде такою ж, як і кількість коливальних режимів (\(3N - 5\) or \(3N - 6\), depending on whether the molecule is linear or non-linear). This requirement is satisfied in the \(H_2O\) example above. For a less straightforward example, consider the methane molecule, \(CH_4\). It might appear that we could choose a basis made up of the four \(C\)-\(H\) bond lengths and the six \(H\)-\(C\)-\(H\) bond angles. However, this would give us \(10\) basis functions, and \(CH_4\) has only \(9\) vibrational modes. This is due to the fact that the bond angles are not all independent of each other. It can be tricky to come up with the appropriate internal coordinate basis to describe all of the molecular motions, but all is not lost. Even if you can’t work out the appropriate bond angles to choose, you can always take a basis of bond lengths to investigate the stretching vibrations of a molecule. If you want to know the symmetries of the bending vibrations, you can use the \(3N\) Cartesian basis method to determine the symmetries of all of the vibrational modes and compare these with the stretching mode symmetries to identify the bending modes.
