1.9: Матриці перетворення

Last updated
Save as PDF

Page ID: 17548

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Матриці можуть бути використані для відображення одного набору координат або функцій на інший набір. Матриці, що використовуються для цієї мети, називаються матрицями перетворення. У теорії груп ми можемо використовувати матриці перетворення для виконання різних операцій симетрії, розглянутих на початку курсу. Як простий приклад, ми дослідимо матриці, які ми використовували б для виконання деяких з цих операцій симетрії над вектором\(\begin{pmatrix} x, y \end{pmatrix}\).

Операція ідентичності

Операція ідентичності залишає вектор без змін, і, як ви вже можете підозрювати, відповідною матрицею є матриця ідентичності.

\[\begin{pmatrix} x, y \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} x, y \end{pmatrix} \label{9.1}\]

Відображення в площині

Найпростіший приклад матриці відображення відповідає відображенню вектора\(\begin{pmatrix} x, y \end{pmatrix}\) in either the \(x\) or \(y\) axes. Reflection in the \(x\) axis maps \(y\) to \(-y\), while reflection in the \(y\) axis maps \(x\) to \(-x\). The appropriate matrix is very like the identity matrix but with a change in sign for the appropriate element. Reflection in the \(x\) axis transforms the vector \(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} x, -y \end{pmatrix}\), and the appropriate matrix is

\[\begin{pmatrix} x, y \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = \begin{pmatrix} x, -y \end{pmatrix} \label{9.2}\]

альт — Малюнок\(\PageIndex{1}\): Відображення по осі x

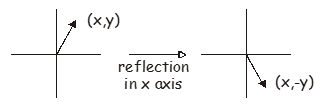
Відображення по осі y перетворює вектор\(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} -x, y \end{pmatrix}\), and the appropriate matrix is

\[\begin{pmatrix} x, y \end{pmatrix} \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} -x, y \end{pmatrix} \label{9.3}\]

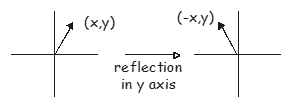
Більш загально матриці можуть використовуватися для представлення відображень у будь-якій площині (або лінії в 2D). Наприклад, відображення по осі 45°, показане під картами

\(\begin{pmatrix} x, y \end{pmatrix}\) onto \(\begin{pmatrix} -y, -x \end{pmatrix}\).

\[\begin{pmatrix} x, y \end{pmatrix} \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix} = \begin{pmatrix} -y, -x \end{pmatrix} \label{9.4}\]

Обертання навколо осі

У двох вимірах відповідна матриця для представлення повороту на кут\(\theta\) щодо початку

\[R(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \label{9.5}\]

У трьох вимірах обертання про\(x\), \(y\) and \(z\) axes acting on a vector \(\begin{pmatrix} x, y, z \end{pmatrix}\) are represented by the following matrices.

\[R_{x}(\theta) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{pmatrix} \label{9.6a}\]

\[R_{y}(\theta) = \begin{pmatrix} \cos\theta & 0 & -\sin\theta \\ 0 & 1 & 0 \\ \sin\theta & 0 & \cos\theta \end{pmatrix} \label{9.6b}\]

\[R_{z}(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \label{9.6c}\]