1.8: Огляд матриць

Визначення

\(n \times m\)Матриця - це двовимірний масив чисел з\(n\) рядками і\(m\) стовпцями. Цілі числа\(n\) і\(m\) називаються розмірами матриці. Якщо\(n = m\) тоді матриця квадратна. Числа в матриці відомі як елементи матриці (або просто елементи) і зазвичай даються індекси для позначення їх положення в матриці, наприклад, елемент\(a_{ij}\) буде займати\(i^{th}\) рядок і\(j^{th}\) стовпець матриці. Наприклад:

\[M = \left(\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right) \label{8.1}\]

являє собою\(3 \times 3\) матрицю з\(a_{11}=1\),\(a_{12}=2\),\(a_{21}=4\) і\(a_{13}=3\) т.д.

У квадратній матриці діагональними елементами вважаються ті, для яких\(i\) =\(j\) (числа\(1\)\(5\), і\(9\) в наведеному вище прикладі). Недіагональні елементи - це ті\(2\), для яких\(i \neq j\) (\(3\)\(4\),\(6\),\(7\),, і\(8\) в наведеному вище прикладі). Якщо всі позадіагональні елементи рівні нулю, то маємо діагональну матрицю. Пізніше ми побачимо, що діагональні матриці мають значне значення в теорії груп.

Одинична матриця або ідентифікаційна матриця (зазвичай дається символом\(I\)) - це діагональна матриця, в якій всі діагональні елементи рівні\(1\). Одинична матриця, що діє на іншу матрицю, не має ефекту — вона така ж, як операція ідентичності в теорії груп і аналогічна множенню числа на\(1\) в повсякденній арифметиці.

\(A^T\)Транспонування матриці\(A\) - це матриця, яка є результатом зміни між усіма рядками та стовпцями. Симетрична матриця така ж, як і її транспонування (\(A^T=A\)тобто\(a_{ij} = a_{ji}\) для всіх значень\(i\) і\(j\)). Транспонування матриці\(M\) вище (яка не є симетричною)

\[M^{T} = \left(\begin{array}{ccc} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{array}\right) \label{8.2}\]

Сума діагональних елементів в квадратній матриці називається слідом (або символом) матриці (для наведеної вище матриці слід\(\chi = 1 + 5 + 9 = 15\)). Сліди матриць, що представляють операції симетрії, будуть мати велике значення в теорії груп.

Вектор - це всього лише окремий випадок матриці, в якій одна з вимірів дорівнює\(1\). \(n \times 1\)Матриця - це вектор-стовпчик;\(1 \times m\) матриця - вектор-рядок. Компоненти вектора зазвичай позначаються лише одним індексом. Одиничний вектор має один елемент рівний,\(1\) а інші рівні нулю (він збігається з одним рядком або стовпцем ідентифікаційної матриці). Ми можемо розширити ідею далі, щоб сказати, що одне число - це матриця (або вектор) розмірності\(1 \times 1\).

Матрична алгебра

1. Дві матриці з однаковими розмірами можуть бути додані або віднімані шляхом додавання або віднімання елементів, що займають однакову позицію в кожній матриці. напр.

\[A = \begin{pmatrix} 1 & 0 & 2 \\ 2 & 2 &1 \\ 3 & 2 & 0 \end{pmatrix} \label{8.3}\]

\[B = \begin{pmatrix} 2 & 0 & -2 \\ 1 & 0 & 1 \\ 1 & -1 & 0 \end{pmatrix} \label{8.4}\]

\[A + B = \begin{pmatrix} 3 & 0 & 0 \\ 3 & 2 & 2 \\ 4 & 1 & 0 \end{pmatrix} \label{8.5}\]

\[A - B = \begin{pmatrix} -1 & 0 & 4 \\ 1 & 2 & 0 \\ 2 & 3 & 0 \end{pmatrix} \label{8.6}\]

2. Матрицю можна помножити на константу шляхом множення кожного елемента на константу.

\[4B = \left(\begin{array}{ccc} 8 & 0 & -8 \\ 4 & 0 & 4 \\ 4 & -4 & 0 \end{array}\right) \label{8.7}\]

\[3A = \left(\begin{array}{ccc} 3 & 0 & 6 \\ 6 & 6 & 3 \\ 9 & 6 & 0 \end{array}\right) \label{8.8}\]

3. Дві матриці можна помножити разом за умови, що кількість стовпців першої матриці збігається з кількістю рядків другої матриці, тобто\(n \times m\) матрицю можна помножити на\(m \times l\) матрицю. Отримана матриця матиме розміри\(n \times l\). Щоб знайти елемент\(a_{ij}\) в матриці добутку, беремо точковий добуток рядка\(i\) першої матриці і\(j\) стовпця другої матриці (тобто множимо послідовні елементи разом з рядка\(i\) першої матриці і стовпчика\(j\) другої матриці) і складаємо їх. разом тобто\(c_{ij}\) =\(\Sigma_k\)\(a_{ik}\)\(b_{jk}\) напр. у\(3 \times 3\) матрицях\(A\) і\(B\) використовується в наведених вище прикладах, перший елемент у матриці\(C = AB\) добутку\(c_{11}\) =\(a_{11}\)\(b_{11}\) +\(a_{12}\)\(b_{21}\) +\(a_{13}\)\(b_{31}\)

\[AB = \begin{pmatrix} 1 & 0 & 2 \\ 2 & 2 & 1 \\ 3 & 2 & 0 \end{pmatrix} \begin{pmatrix} 2 & 0 & -2 \\ 1 & 0 & 1 \\ 1 & -1 & 0 \end{pmatrix} = \begin{pmatrix} 4 & -2 & -2 \\ 7 & -1 & -2 \\ 8 & 0 & -4 \end{pmatrix} \label{8.9}\]

Прикладом матриці множення вектора є

\[A\textbf{v} = \begin{pmatrix} 1 & 0 & 2 \\ 2 & 2 & 1 \\ 3 & 2 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 7 \\ 9 \\ 7 \end{pmatrix} \label{8.10}\]

Множення матриць, як правило, не є комутативним, властивістю, яка відображає поведінку, знайдену раніше для операцій симетрії всередині групи точок.

Прямі продукти

Прямий добуток двох матриць (з урахуванням символу\(\otimes\)) - особливий тип матричного добутку, який генерує матрицю вищої розмірності, якщо обидві матриці мають розмірність більше одиниці. Найпростіше продемонструвати, як побудувати прямий добуток двох матриць\(A\) і\(B\) на прикладі:

\[ \begin{align} A \otimes B &= \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \otimes \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} \\[4pt] &= \begin{pmatrix} a_{11}B & a_{12}B \\ a_{21}B & a_{22}B \end{pmatrix} \\[4pt] &= \begin{pmatrix} a_{11}b_{11} & a_{11}b_{12} & a_{12}b_{11} & a_{12}b_{12} \\ a_{11}b_{21} & a_{11}b_{22} & a_{12}b_{21} & a_{12}b_{22} \\ a_{21}b_{11} & a_{21}b_{12} & a_{22}b_{11} & a_{22}b_{21} \\ a_{21}b_{21} & a_{21}b_{22} & a_{22}b_{21} & a_{22}b_{22} \end{pmatrix} \label{8.11} \end{align} \]

Хоча це може здатися дещо дивною операцією для здійснення, прямі продукти виростають багато в теорії груп.

Зворотні матриці та детермінанти

Якщо дві квадратні матриці\(A\) і\(B\) помножити разом, щоб дати ідентичність матриці I (тобто\(AB = I\)), то кажуть,\(B\) що це зворотна\(A\) (записана\(A^{-1}\)). Якщо\(B\) є зворотним,\(A\) то також\(A\) є зворотним\(B\). Нагадаємо, що однією з умов, що накладаються на операції симетрії в групі, є те, що кожна операція повинна мати зворотну. За аналогією випливає, що будь-які матриці, які ми використовуємо для представлення елементів симетрії, також повинні мати зворотні. Виходить, що квадратна матриця має зворотну тільки в тому випадку, якщо її детермінант ненульовий. З цієї причини (та інших, які стануть очевидними пізніше, коли нам потрібно вирішити рівняння за участю матриць) нам потрібно трохи дізнатися про матричні детермінанти та їх властивості.

Для кожної квадратної матриці існує унікальна функція всіх елементів, яка дає одне число, яке називається детермінантою. Спочатку, мабуть, не буде особливо очевидно, чому це число має бути корисним, але матричні детермінанти мають велике значення як в чистій математиці, так і в ряді областей науки. Історично склалося, що детермінанти насправді були навколо перед матрицями. Вони виникли спочатку як властивість системи лінійних рівнянь, яка «визначала», чи має система унікальне рішення. Як ми побачимо пізніше, коли така система рівнянь переформується як матричне рівняння, ця властивість переноситься в матричний детермінант.

Існує два різних визначення детермінанти, одне геометричне і одне алгебраїчне. У геометричній інтерпретації числа в кожному рядку\(n \times n\) матриці розглядаються як координати в\(n\) -мірному просторі. В одновимірній матриці (тобто число) існує лише одна координата, а детермінант можна інтерпретувати як (підписану) довжину вектора від початку до цієї точки. Для\(2 \times 2\) матриці ми маємо дві координати в площині, а визначник - це (підписана) площа паралелограма, яка включає ці дві точки та початок. Для\(3 \times 3\) матриці визначником є (підписаний) об'єм паралелепіпеда, який включає три точки (у тривимірному просторі), визначені матрицею та початком. Це проілюстровано нижче. Ідея поширюється на більш високі розміри аналогічним чином. Отже, у певному сенсі детермінант пов'язаний з розміром матриці.

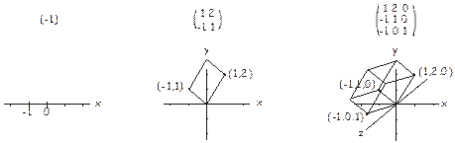
Алгебраїчне визначення детермінанти\(nxn\) матриці - це сума над усіма можливими добутками (перестановками) n елементів, взятих з різних рядків і стовпців. Кількість членів у сумі дорівнює\(n!\) кількості можливих перестановок\(n\) значень (тобто\(2\) для\(2 \times 2\) матриці,\(6\) для\(3 \times 3\) матриці тощо). Кожному члену в сумі дається позитивний або негативний знак в залежності від того, парне чи непарне число інверсій перестановок у творі. Інверсія перестановки - це всього лише пара елементів, які вийшли з ладу, коли описані їх індексами. Наприклад, для набору з чотирьох елементів\(\begin{pmatrix} a_1, a_2, a_3, a_4 \end{pmatrix}\) перестановка\(a_1 a_2 a_3 a_4\) має всі елементи в їх правильному порядку (тобто в порядку збільшення індексу). Однак перестановка\(a_2 a_4 a_1 a_3\) містить інверсії перестановки\(a_2 a_1\),\(a_4 a_1\),\(a_4 a_3\).

Наприклад, для двовимірної матриці

\[\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \label{8.12}\]

де індекси позначають позиції рядків і стовпців елементів,\(2\) можливі продукти/перестановки за участю елементів з різних рядків і стовпців,\(a_{11}\)\(a_{22}\) і\(a_{12}\)\(a_{21}\). У другому семестрі існує інверсія перестановки за участю індексів стовпців\(2\) і\(1\) (інверсії перестановки за участю індексів рядків і стовпців слід шукати окремо), тому цей термін приймає негативний знак, а детермінант\(a_{11}\)\(a_{22}\) -\(a_{12}\)\(a_{21}\).

Для\(3 \times 3\) матриці

\[\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \label{8.13}\]

можливі комбінації елементів з різних рядків і стовпців разом зі знаком з числа перестановок, необхідних для розміщення їх індексів в числовому порядку, такі:

\[\begin{array}{rl}a_{11} a_{22} a_{33} & (0 \: \text{inversions}) \\ -a_{11} a_{23} a_{32} & (1 \: \text{inversion -} \: 3>2 \: \text{in the column indices}) \\ -a_{12} a_{21} a_{33} & (1 \: \text{inversion -} \: 2>1 \: \text{in the column indices}) \\ a_{12} a_{23} a_{31} & (2 \: \text{inversions -} \: 2>1 \: \text{and} \: 3>1 \: \text{in the column indices}) \\ a_{13} a_{21} a_{32} & (2 \: \text{inversions -} \: 3>1 \: \text{and} \: 3>2 \: \text{in the column indices}) \\ -a_{13} a_{22} a_{31} & (3 \: \text{inversions -} \: 3>2, 3>1, \: \text{and} \: 2>1 \: \text{in the column indices}) \end{array} \label{8.14}\]

а детермінант - це просто сума цих термінів.

Це все може здатися трохи складним, але на практиці існує досить систематична процедура обчислення детермінант. Визначник\(A\) матриці зазвичай пишеться det (\(A\)) або |\(a\) |.

Для\(2 \times 2\) матриці

\[A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}; det(A) = |A| = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc \label{8.15}\]

Для\(3 \times 3\) матриці

\[B = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}; det(B) = a\begin{vmatrix} e & f \\ h & i \end{vmatrix} - b\begin{vmatrix} d & f \\ g & i \end{vmatrix} + c\begin{vmatrix} d & e \\ g & h \end{vmatrix} \label{8.16}\]

Для\(4x4\) матриці

\[C = \begin{pmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{pmatrix}; det(C) = a\begin{vmatrix} f & g & h \\ j & k & l \\ n & o & p \end{vmatrix} - b\begin{vmatrix} e & g & h \\ i & k & l \\ m & o & p \end{vmatrix} + c\begin{vmatrix} e & f & h \\ i & j & l \\ m & n & p \end{vmatrix} - d\begin{vmatrix} e & f & g \\ i & j & k \\ m & n & o \end{vmatrix} \label{8.17}\]

і так далі в більш високих розмірах. Зауважте, що підматриці у наведеному вище\(3 \times 3\) прикладі - це лише матриці, сформовані з початкової матриці\(B\), які не містять елементів з того ж рядка чи стовпця, що й коефіцієнти попереднього множення з першого рядка.

Матричні детермінанти мають ряд важливих властивостей:

1. Визначником матриці ідентичності є\(1\).

\[e.g. \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} = \begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} = 1 \label{8.18}\]

2. Детермінант матриці такий же, як і визначник її транспонування, тобто det (\(a\)) = det (\(A^{T}\))

\[e.g. \begin{vmatrix} a & b \\ c & d \end{vmatrix} = \begin{vmatrix} a & c \\ b & d \end{vmatrix} \label{8.19}\]

3. Знак визначника зміни, коли будь-які два рядки або будь-які два стовпці змінюються місцями

\[e.g. \begin{vmatrix} a & b \\ c & d \end{vmatrix} = -\begin{vmatrix} b & a \\ d & c \end{vmatrix} = -\begin{vmatrix} c & d \\ a & b \end{vmatrix} = \begin{vmatrix} d & c \\ b & a \end{vmatrix} \label{8.20}\]

4. Визначник дорівнює нулю, якщо будь-який рядок або стовпчик повністю дорівнює нулю, або якщо будь-які два рядки або стовпці рівні або кратні один одному.

\[e.g. \begin{vmatrix} 1 & 2 \\ 0 & 0 \end{vmatrix} = 0, \begin{vmatrix} 1 & 2 \\ 2 & 4 \end{vmatrix} = 0 \label{8.21}\]

5. Визначник не змінюється шляхом додавання будь-якої лінійної комбінації рядків (або стовпців) до іншого рядка (або стовпця).
6. Визначник добутку двох матриць такий же, як добуток детермінант двох матриць, тобто det (\(AB\)) = det () det (\(A\)) det (\(B\)).

Вимога, що для того, щоб матриця мала зворотну, вона повинна мати ненульовий детермінант, випливає з властивості vi). Як уже згадувалося раніше, добуток матриці та її зворотний видає матрицю ідентичності I. Тому ми маємо:

\[\begin{array}{rcl} det(A^{-1} A) = det(A^{-1}) det(A) & = & det(I) \\ det(A^{-1}) & = & det(I)/det(A) = 1/det(A) \end{array} \label{8.22}\]

Звідси випливає, що матриця\(A\) може мати обернену лише тоді, коли її детермінант ненульовий, інакше визначник її зворотного буде невизначений.