1.10: Матричні зображення груп

Тепер ми готові інтегрувати те, що ми щойно дізналися про матриці, з груповою теорією. Операції симетрії в групі можуть бути представлені набором матриць перетворення\(\Gamma\)\((g)\), по одній для кожного елемента симетрії\(g\). Кожна окрема матриця називається представником відповідної операції симетрії, а повний набір матриць називається матричним представленням групи. Представники матриць діють на деякому обраному базовому наборі функцій, а фактичні матриці, що складають дане уявлення, залежатимуть від обраної основи. Тоді подання, як кажуть, охоплює обрану основу. У наведених вище прикладах ми розглядали вплив деяких простих матриць перетворення на довільний вектор\(\begin{pmatrix} x, y \end{pmatrix}\). Таким чином, основою була пара одиничних векторів, що вказують в\(y\) напрямках\(x\) і. У більшості прикладів, які ми розглянемо в цьому курсі, ми будемо використовувати набори атомних орбіталів як базові функції для матричних уявлень. Не хвилюйтеся, якщо ці ідеї зараз здадуться трохи абстрактними - вони повинні стати зрозумілішими в наступному розділі, коли ми розглянемо деякі приклади.

Перш ніж продовжувати далі, ми повинні перевірити, чи матричне представлення групи відповідає всім правилам, викладеним у формальному математичному визначенні групи.

1. Перше правило полягає в тому, що група повинна включати операцію ідентичності\(E\) (операція «нічого не робити»). Вище ми показали, що матричний представник операції ідентичності - це просто матриця ідентичності. Як наслідок, кожне представлення матриці включає відповідну матрицю ідентичності.
2. Друге правило полягає в тому, що комбінація будь-якої пари елементів також повинна бути елементом групи (властивістю group). Якщо помножити разом будь-які два представника матриці, ми повинні отримати нову матрицю, яка є представником іншої операції симетрії групи. Фактично, матричні представники розмножуються разом, щоб дати нових представників точно так само, як операції симетрії об'єднуються відповідно до таблиці множення груп. Наприклад, у\(C_{3v}\) точковій групі ми показали, що комбінована операція симетрії\(C_3\)\(\sigma_v\) еквівалентна \(\sigma_v''\). У матричному поданні групи, якщо матричні представники\(C_3\) і \(\sigma_v\)множаться разом, то результат буде представником \(\sigma_v''\).
3. Третє правило стверджує, що кожна операція повинна мати зворотну, яка також є членом групи. Комбінований ефект від проведення операції та її зворотний такий же, як і операція ідентичності. Досить легко показати, що матричні представники задовольняють цьому критерію. Наприклад, зворотне відображення - це інше відображення, ідентичне першому. Отже, у матричному терміні ми очікуємо, що матриця відображення є власною зворотною, і що дві однакові матриці відображення, помножені разом, дадуть матрицю ідентичності. Це виявляється правдою, і можна перевірити, використовуючи будь-яку з матриць відображення в прикладах вище. Обернена матриця обертання - це інша матриця обертання, що відповідає обертанню протилежного сенсу до першої.
4. Заключне правило говорить, що правило поєднання елементів симетрії в групі має бути асоціативним. Це автоматично задовольняється правилами множення матриць.

Приклад: матричне уявлення\(C_{3v}\) точкової групи (молекули аміаку)

Перше, що нам потрібно зробити, перш ніж ми зможемо побудувати матричне уявлення, це вибрати основу. Для\(NH_3\), we will select a basis \(\begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix}\) that consists of the valence s orbitals on the nitrogen and the three hydrogen atoms. We need to consider what happens to this basis when it is acted on by each of the symmetry operations in the \(C_{3v}\) point group, and determine the matrices that would be required to produce the same effect. The basis set and the symmetry operations in the \(C_{3v}\) point group are summarized in the figure below.

Наслідки операцій симетрії на обраній нами основі такі:

\[\begin{array}{ll} E & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \rightarrow \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \\ C_3^+ & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \rightarrow \begin{pmatrix} s_N, s_2, s_3, s_1 \end{pmatrix} \\ C_3^- & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \rightarrow \begin{pmatrix} s_N, s_3, s_1, s_2 \end{pmatrix} \\ \sigma_v & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \rightarrow \begin{pmatrix} s_N, s_1, s_3, s_2 \end{pmatrix} \\ \sigma_v' & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \rightarrow \begin{pmatrix} s_N, s_2, s_1, s_3 \end{pmatrix} \\ \sigma_v'' & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \rightarrow \begin{pmatrix} s_N, s_3, s_2, s_1 \end{pmatrix} \end{array} \label{10.1}\]

За допомогою огляду матрицями, які здійснюють однакові перетворення, є:

\[\begin{array}{ll} \Gamma(E) & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \\ \Gamma(C_3^+) & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} = \begin{pmatrix} s_N, s_2, s_3, s_1 \end{pmatrix} \\ \Gamma(C_3^-) & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{pmatrix} = \begin{pmatrix} s_N, s_3, s_1, s_2 \end{pmatrix} \\ \Gamma(\sigma_v) & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} = \begin{pmatrix} s_N, s_1, s_3, s_2 \end{pmatrix} \\ \Gamma(\sigma_v') & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} s_N, s_2, s_1, s_3 \end{pmatrix} \\ \Gamma(\sigma_v'') & \begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix} = \begin{pmatrix} s_N, s_3, s_2, s_1 \end{pmatrix} \end{array} \label{10.2}\]

Таким чином, ці шість матриць утворюють уявлення для\(C_{3v}\) point group in the \(\begin{pmatrix} s_N, s_1, s_2, s_3 \end{pmatrix}\) basis. They множення разом відповідно до таблиці групового множення і задовольняють всім вимогам до математичної групи.

Ми написали вектори, що представляють нашу основу у вигляді рядкових векторів. Це важливо. Якби ми писали їх як вектори стовпців, відповідні матриці перетворення були б транспозами матриць вище, і не відтворювали б таблицю групового множення (спробуйте це як вправу, якщо вам потрібно переконати себе).

Приклад: матричне зображення\(C_{2v}\) точкової групи (алліловий радикал)

У цьому прикладі ми візьмемо за основу a\(p\) orbital on each carbon atom \(\begin{pmatrix} p_1, p_2, p_3 \end{pmatrix}\).

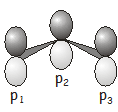
Зверніть увагу, що\(p\) orbitals are perpendicular to the plane of the carbon atoms (this may seem obvious, but if you’re visualizing the basis incorrectly it will shortly cause you a not inconsiderable amount of confusion). The symmetry operations in the \(C_{2v}\) point group, and their effect on the three \(p\) orbitals, are as follows:

\[\begin{array}{ll} E & \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \rightarrow \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \\ C_2 & \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \rightarrow \begin{pmatrix} -p_3, -p_2, -p_1 \end{pmatrix} \\ \sigma_v & \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \rightarrow \begin{pmatrix} -p_1, -p_2, -p_3 \end{pmatrix} \\ \sigma_v' & \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \rightarrow \begin{pmatrix} p_3, p_2, p_1 \end{pmatrix} \end{array} \label{10.3}\]

Матриці, які здійснюють перетворення, є

\[\begin{array}{ll} \Gamma(E) & \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \\ \Gamma(C_2) & \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \begin{pmatrix} 0 & 0 & -1 \\ 0 & -1 & 0 \\ -1 & 0 & 0 \end{pmatrix} = \begin{pmatrix} -p_3, -p_2, -p_1 \end{pmatrix} \\ \Gamma(\sigma_v) & \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} = \begin{pmatrix} -p_1, -p_2, -p_3 \end{pmatrix} \\ \Gamma(\sigma_v') & \begin{pmatrix} p_1, p_2, p_3 \end{pmatrix} \begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix} = \begin{pmatrix} p_3, p_2, p_1 \end{pmatrix} \end{array} \label{10.4}\]