3.2: Певний інтеграл
- Page ID
- 60249
Відстань від швидкості
Припустимо, автомобіль їде по прямій дорозі з постійною швидкістю 40 миль на годину протягом двох годин. Див. Графік його швидкості нижче. Як далеко це зайшло?
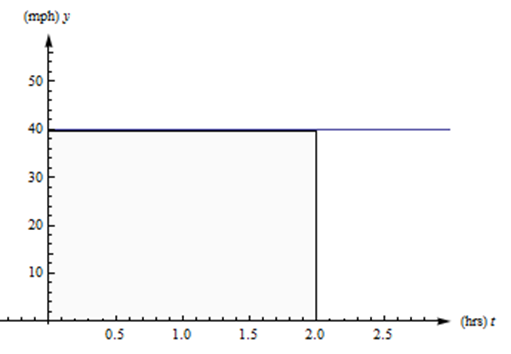
Рішення
Ми всі пам'ятаємо відстань =\( \cdot \) час швидкості, так що це легко. Автомобіль поїхав (40 миль/год)\( \cdot \) (2 години) = 80 миль.
Тепер припустимо, що автомобіль їде так, що його швидкість стабільно зростає від 0 до 40 миль на годину, протягом двох годин. (Просто будьте вдячні, що ви не застрягли за цією машиною на шосе.) Дивіться графік його швидкості нижче. Як далеко зайшов цей автомобіль?
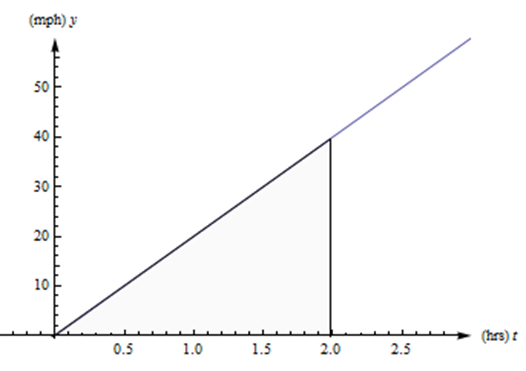
Рішення
Проблема з нашим старим надійним відстанню = співвідношення\( \cdot \) часу швидкості полягає в тому, що він працює лише в тому випадку, якщо швидкість постійна. Якщо швидкість змінюється, немає хорошого способу використовувати цю формулу.
Але подивіться на графік з останнього прикладу ще раз. Зверніть увагу, що відстань =\( \cdot \) час швидкості також описує область між графіком швидкості і\(t\) -віссю, між\(t = 0\)\(t = 2\) годинами. Швидкість - це висота прямокутника, час - довжина прямокутника, а відстань - площа прямокутника. Таким чином ми можемо розширити нашу просту формулу для обробки більш складних швидкостей: І саме так ми можемо відповісти на другий приклад.
Відстань, яку проїжджає автомобіль, - це область між його графіком швидкості,\(t\) -віссю,\(t = 0\) і\(t = 2\). Цей регіон є трикутником, тому його площа\[\frac{1}{2}bh = \frac{1}{2}(2 \text{ hours})(40 \text{ miles per hour}) = 40 \text{ miles}.\nonumber \] Таким чином, автомобіль проїжджає 40 миль під час своєї дратівливої поїздки.
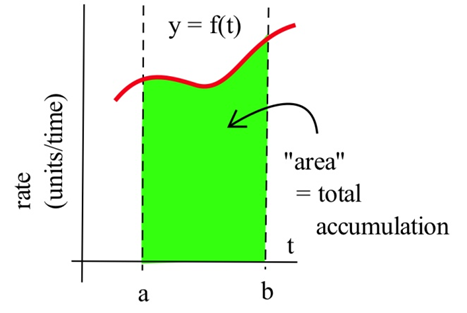
У наших прикладах відстань/швидкості функція представляла швидкість руху (милі на годину), а площа представляла загальну пройдену відстань. Цей принцип працює в більш загальному плані:
Для функцій, що представляють інші темпи, такі як виробництво заводу (велосипеди на день) або потік води в річці (галони в хвилину) або рух через міст (автомобілі в хвилину), або поширення хвороби (щойно хворі люди на тиждень), площа все одно буде представляти загальну кількість чогось.
На графіку нижче показана швидкість потоку (кубічні фути в секунду) води в річці Скайкоміш в містечку Голдбар у штаті Вашингтон.
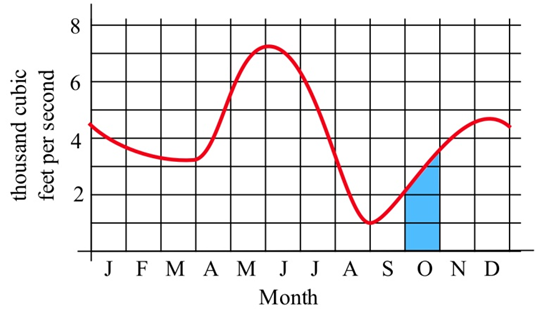
Рішення
Площа затіненої області являє собою загальний обсяг (кубічні фути або\( \text{ft}^3 \)) води, що протікає повз місто протягом жовтня місяця. Ми можемо наблизити цю область до наближення загальної води, думаючи про затінену область як прямокутник з трикутником зверху.
\[ \begin{align*} \text{Total water } & = \text{ total area}\\ & \approx \text{ area of rectangle }+\text{ area of the "triangle"} \\ & \approx \left(2000 \frac{\text{ft}^3}{\text{s}}\right)\left(30 \text{ days}\right)+\frac{1}{2}\left(1500\frac{\text{ft}^3}{\text{s}}\right)\left(30\text{ days}\right) \\ & = \left(2570\frac{\text{ft}^3}{\text{s}}\right)\left(30\text{ days}\right) \end{align*} \nonumber \]
Зауважте, що нам потрібно перетворити одиниці, щоб зрозуміти наш результат:\[ \begin{align*} \text{Total water } & \approx \left(2570\frac{\text{ft}^3}{\text{s}}\right)\left(30\text{ days}\right) \\ & = \left(2570\frac{\text{ft}^3}{\text{s}}\right)\left(2,\!592,\!000\text{ sec}\right) \\ & \approx 7.128\cdot 10^9\text{ ft}^3 \end{align*} \nonumber \]
Близько 7 мільярдів кубічних футів води протікали повз Goldbar в жовтні.
Наближення з прямокутниками
Як ми наближаємо площу, якщо крива швидкості, ну, крива
? Ми могли б використовувати прямокутники і трикутники, як ми робили в останньому прикладі. Але виявляється корисніше (і простіше) просто використовувати прямокутники. Чим більше прямокутників ми використовуємо, тим краще наше наближення.
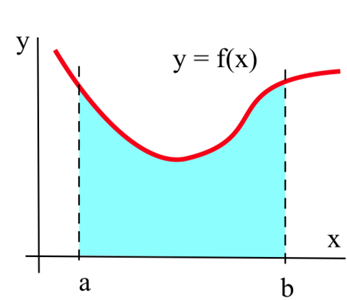
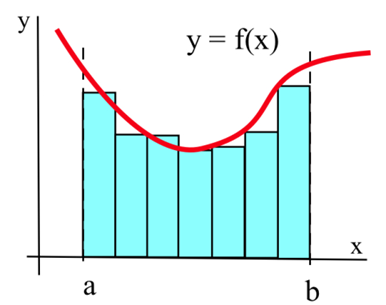
Припустимо, ми хочемо обчислити площу між графіком позитивної функції\(f\) і\(x\) -віссю на інтервалі\([a, b]\) (на графіку вище). Метод Рімана Сума полягає у побудові декількох прямокутників з основами на інтервалі\([a, b]\) та сторонам, які доходять до графіка\(f\) (див. Нижче). Потім площі прямокутників можна обчислити та скласти разом, щоб отримати число, яке називається Riemann Sum of\(f\) on\([a, b]\). Площа області, утвореної прямокутниками, - це наближення потрібної нам площі.
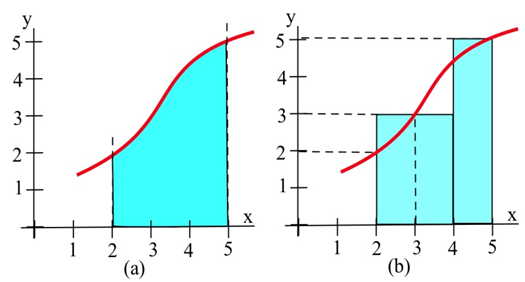
Наблизимо площу на графіку зліва між графом\(f\) і\(x\) -віссю на інтервалі [2, 5] шляхом підсумовування площ прямокутників на графіку праворуч.
Рішення
Загальна площа прямокутників дорівнює\[(2)(3) + (1)(5) = 11\text{ units}^2.\nonumber \]
\(A\)Дозволяти область обмежена графіком\(f(x) = \frac{1}{x}\),\(x\) -вісь, і вертикальні лінії в\(x = 1\) і\(x = 5\). Ми не можемо точно знайти область (з тим, що ми знаємо зараз), але ми можемо наблизити її за допомогою прямокутників.
Коли ми робимо наші прямокутники, у нас є багато варіантів. Ми могли б вибрати будь-які (не перекриваються) прямокутники, чиї днища лежать в інтервалі на осі х, і чиї вершини перетинаються з кривою десь. Але найпростіше вибрати прямокутники, які (а) мають однакову ширину і (б) беруть свої висоти від функції на одному краю. Нижче наведені графіки, що показують два способи використання чотирьох прямокутників для наближення цієї області. На першому графіку ми використовували ліві кінцеві точки; висота кожного прямокутника походить від значення функції на її лівому краю. На другому графіку на наступній сторінці ми використовували праві кінцеві точки.
Ліві кінцеві точки: Площа приблизно дорівнює сумі площ прямокутників. Кожен прямокутник отримує свою висоту від функції,\( f(x)=\frac{1}{x} \) а кожен прямокутник має ширину 1.
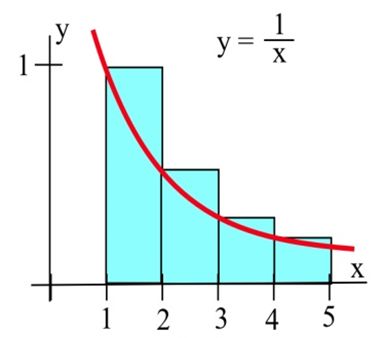
Ви можете знайти площу кожного прямокутника, використовуючи область =\( \cdot \) ширина висоти. Таким чином, загальна площа прямокутників, ліва оцінка площі під кривою, є\[f(1)\cdot 1+f(2)\cdot 1+f(3)\cdot 1+f(4)\cdot 1=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{25}{12}\approx 2.08.\nonumber \]
Зверніть увагу, що оскільки ця функція зменшується, всі ліві прямокутники кінцевої точки стирчать над потрібною областю - використання лівих кінцевих точок переоцінює площу.
Правосторонні кінцеві точки: правою оцінкою площі є\[f(2)\cdot 1+f(3)\cdot 1+f(4)\cdot 1+f(5)\cdot 1=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\frac{77}{60}\approx 1.28.\nonumber \]
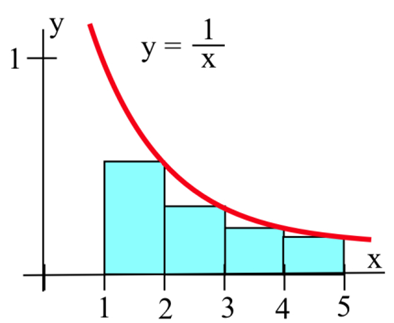
Всі праві прямокутники лежать повністю під кривою, тому ця оцінка буде заниженою.
Ми бачимо, що справжня площа насправді знаходиться між цими двома оцінками. Таким чином, ми могли б взяти їх середнє:\[\text{Average}=\frac{\frac{25}{12}+\frac{77}{60}}{2}=\frac{101}{60}\approx 1.68\nonumber \]
Загалом, середнє значення лівої і правої оцінок буде ближче до реальної площі, ніж будь-яка індивідуальна оцінка.
Наша оцінка площі під кривою становить близько 1,68. (Фактична площа становить близько 1,61.)
Цей аплет дозволить вам побачити, як змінюється наближення, якщо ви використовуєте більше прямокутників; змініть повзунок положення
, щоб перемикатися між лівими кінцевими точками, правими кінцевими точками та середніми точками:
Якби ми хотіли отримати кращу відповідь, ми могли б використовувати ще більше і навіть більш вузькі прямокутники. Але є межа тому, скільки роботи ми хочемо зробити вручну. На практиці вибирайте керовану кількість прямокутників. У нас будуть кращі методи, щоб отримати більш точні відповіді найближчим часом.
Ці суми площ прямокутників називаються сумами Рімана. Ви можете побачити стенографічне позначення, яке використовується, коли люди говорять про суми. Ми не будемо багато використовувати його в цій книзі, але ви повинні знати, що це означає.
Ріман Сум
Сума Рімана для функції\(f(x)\) за інтервал\([a, b]\) - це сума площ прямокутників, яка наближає площу під кривою. Почніть з поділу інтервалу\([a, b]\) на\(n\) підінтервали; кожен підінтервал буде основою одного прямокутника. Зазвичай робимо всі прямокутники однакової ширини\( \Delta x \). Висота кожного прямокутника походить від функції, оціненої в певний момент його підінтервалу. Тоді сума Рімана є\[f(x_1)\Delta x+f(x_2)\Delta x+f(x_3)\Delta x+\dots +f(x_n)\Delta x\nonumber \] або, враховуючи\( \Delta x \),\[\Delta x\left(f(x_1)+f(x_2)+f(x_3)+\dots +f(x_n)\right).\nonumber \]
Позначення сигми
Прописна грецька буква Sigma\( \sum \) використовується для позначення суми
. Позначення сигми - це спосіб компактно представляти суму багатьох подібних термінів, таких як сума Рімана.
Використовуючи позначення Sigma, можна записати суму Рімана\[\sum\limits_{i=1}^n f\left(x_i\right)\Delta x.\nonumber \]
Це читається вголос як сума, яка\(i\) переходить від 1 до\(n\) з\(f\)\(x\) sub\(i\) разів Дельта\(x\).
\(i\)
Це лічильник або індекс, як ви могли бачити в класі програмування.
Визначення визначеного інтеграла
Оскільки площа під кривою настільки важлива, вона має особливий словниковий запас і позначення.
Певним інтегралом позитивної функції\(f(x)\) протягом інтервалу\([a, b]\) є площа між\(f\),\(x\) -вісь,\(x = a\) і\(x = b\).
Певним інтегралом позитивної функції\(f(x)\) від\(a\) до\(b\) є площа під кривою між\(a\) і\(b\).
Якщо\(f(t)\) являє собою позитивну швидкість (в\(y\) -одиницях на\(t\) -одиниці), то певний інтеграл\(f(t)\) від\(a\) до\(b\) - це загальна\(y\) -одиниці, які накопичуються між\(t = a\) і\(t = b\).
Позначення для визначеного інтеграла
Записується певний інтеграл\(f(x)\)\(b\) від\(a\) до\[\int_a^b f(x)\, dx.\nonumber \]
\( \int \)Символ називається інтегральним знаком; він являє собою витягнуту букву S, що стоїть за сумою
. (\( \int \)Відповідає\( \sum \) від суми Рімана)
\(dx\)На кінці повинні бути включені! The\(dx\) розповідає, що таке змінна — у цьому прикладі змінна є\(x\). (\(dx\)Відповідає\( \Delta x \) від суми Рімана)
Функція\(f\) називається integrand.
\(a\)І\(b\) називаються межами інтеграції.
Форми дієслова
Ми інтегруємо, або знаходимо певний інтеграл функції. Цей процес називається інтеграцією.
Формальне алгебраїчне визначення
\[\int_a^b f(x)\, dx =\lim\limits_{n\to\infty}\sum\limits_{i=1}^n f(x_i)\Delta x.\nonumber \]
Практичне визначення
Певний інтеграл можна наблизити сумою Рімана (діливши площу на прямокутники, де висота кожного прямокутника виходить від функції, обчислюючи площу кожного прямокутника і складаючи їх вгору). Чим більше прямокутників ми використовуємо, тим вужчі прямокутники, тим краще буде наше наближення.
Забігаючи вперед
Незабаром ми матимемо методи обчислення точних значень деяких визначених інтегралів з формул. У багатьох випадках, в тому числі, коли функція дається вам у вигляді таблиці або графіка, вам все одно потрібно буде наблизити певний інтеграл прямокутниками.
На графіку нижче показано\(y = r(t)\), кількість телефонних дзвінків, здійснених за годину у вівторок. Приблизно скільки дзвінків було здійснено між 9 вечора та 11 вечора? Висловіть це як певний інтеграл і наближене з сумою Рімана.
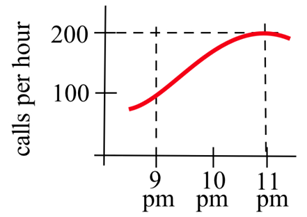
Рішення
Ми знаємо, що накопичені дзвінки будуть областю під цим графіком швидкості протягом цього двогодинного періоду, певним інтегралом цієї ставки від\(t = 9\) до\(t = 11\).
Загальна кількість дзвінків буде\( \int\limits_9^{11} r(t)\,dt \).
Вгорі тут крива, тому ми не можемо отримати точну відповідь. Але ми можемо наблизити площу за допомогою прямокутників. Давайте виберемо чотири прямокутники та ліві кінцеві точки:
\[\int\limits_9^{11} r(t)\,dt \approx 0.5(100+150+180+195)=312.5\nonumber \]
Одиниці викликів на годину\( \cdot \) годин = дзвінки. За нашими оцінками, близько 312 дзвінків було здійснено між 9 вечора та 11 вечора. Це занижена оцінка чи завищена оцінка?
Опишіть площу між графіком\(f(x) = \frac{1}{x}\),\(x\) -віссю та вертикальними лініями при\(x = 1\) і\(x = 5\) як певний інтеграл.
Рішення
Це та сама площа, яку ми оцінювали приблизно 1,68 раніше. Тепер ми можемо використовувати позначення певного інтеграла для його опису. Наша оцінка\( \int\limits_1^5 \frac{1}{x}\, dx \) склала 1,68. Справжнє значення\( \int\limits_1^5 \frac{1}{x}\, dx \) становить близько 1,61.
Використовуючи уявлення про площу, визначте величину\( \int\limits_1^3 1+x \,dx \).
Рішення
\( \int\limits_1^3 1+x \,dx \)являє собою площу між графіком\(f(x) = 1+x\),\(x\) -віссю та вертикальними лініями в 1 і 3.
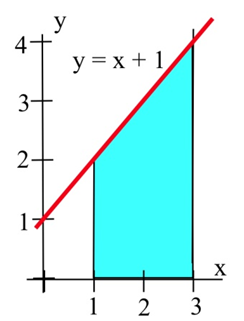
Так як цю область можна розбити на прямокутник і трикутник, ми можемо знайти площу точно. Площа дорівнює\[ 4 + \frac{1}{2}(2)(2) = 6 \text{ units}^2.\nonumber \]
У таблиці наведені темпи приросту населення Беррітауна за кілька років. Скористайтеся цією таблицею для оцінки загального приросту населення з 1970 по 2000 рік:
| Рік,\( t \) | 1970 | 1980 | 1990 | 2000 |
| Темпи приросту населення\( R(t) \) в тисячах людей на рік | 1.5 | 1.9 | 2.2 | 2.4 |
Рішення
Певний інтеграл цієї норми дасть сумарну зміну чисельності населення за тридцятирічний період. У нас є лише кілька частин інформації, тому ми можемо лише оцінити. Незважаючи на те, що ми ще не зробили графік, ми все ще наближаємо область під кривою швидкості, використовуючи прямокутники. Наскільки широкі прямокутники? Ми маємо інформацію кожні 10 років, тому прямокутники мають ширину 10 років. Скільки прямокутників? Будьте обережні тут — це тридцятирічний проміжок, тому є три прямокутника.
- Використання лівих кінцевих точок: (1.5) (10) + (1.9) (10) + (2.2) (10) = 56
- Використання правих кінцевих точок: (1.9) (10) + (2.2) (10) + (2.4) (10) = 65
Беручи середнє з цих двох:\[\frac{56+65}{2}=60.5\nonumber \]
Наша найкраща оцінка загального приросту населення з 1970 по 2000 рік становить 60,5 тис. осіб.
Підписана область
Можливо, ви помітили, що до цього моменту ми наполягали на тому, що integrand (функція, яку ми інтегруємо) бути позитивним. Це тому, що ми говорили про область, яка завжди позитивна.
Якщо висота
(від функції) є від'ємним числом, то множення її на ширину не дає нам фактичної площі, це дає нам область з негативним знаком.
Але виявляється корисно подумати про можливість негативної області. Ми розширимо нашу ідею певного інтеграла зараз, щоб включити integrands, які не завжди можуть бути позитивними. Висоти
прямокутників, значення з функції, тепер не завжди можуть бути позитивними.
Певний інтеграл функції\(f(x)\) за інтервал\([a, b]\) є знаковою областю між\(f\),\(x\) -віссю,\(x = a\) і\(x = b\).
Певний інтеграл функції\(f(x)\) від\(a\) до\(b\) - це підписана область під кривою між\(a\) і\(b\).
Якщо функція позитивна, підписана область є позитивною, як і раніше (і ми можемо назвати її областю.)
Якщо функція опускається нижче\(x\) -осі, області областей нижче\(x\) -осі надходять з негативним знаком. У цьому випадку ми не можемо назвати це просто областю.
Ці негативні області віднімають від певного інтеграла.
\( \int\limits_a^b f(x) \,dx = \)(Площа вище\( x \) -осі)\( - \) (Площа нижче\( x \) -осі)
Якщо\(f(t)\) являє собою позитивну швидкість (в\(y\) -одиницях на\(t\) -одиниці), то певний інтеграл\(f\) від\(a\) до\(b\) - це загальна\(y\) -одиниці, які накопичуються між\(t = a\) і\(t = b\).
Якщо\(f(t)\) являє собою будь-яку ставку (в\(y\) -одиницях на\(t\) -одиниці), то певний інтеграл\(f\) від\(a\) до\(b\) - це чисті\(y\) -одиниці, які накопичуються між\(t = a\) і\(t = b\).
Знайти певний інтеграл\(f(x) = –2\) на інтервалі [1,4].
Рішення
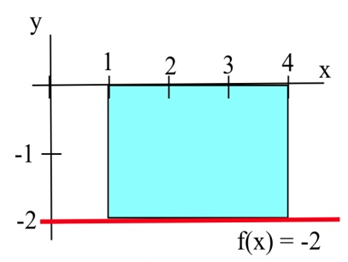
\(\int\limits_1^4 -2\,dx\)це підписана область області, показана праворуч. Область лежить нижче\( x \) -осі, тому область, 6, входить з негативним знаком. Таким чином, певний інтеграл є\(\int\limits_1^4 -2\,dx =-6\).
Негативні ставки свідчать про те, що сума зменшується. Наприклад, якщо\(f(t)\) швидкість руху автомобіля в позитивному напрямку по прямій в часі\(t\) (милі/год), то негативні значення\(f\) вказують на те, що автомобіль рухається в негативному напрямку, назад. Певним інтегралом\(f\) є зміна положення автомобіля протягом часового проміжку. Якщо швидкість позитивна, накопичується позитивна відстань. Якщо швидкість негативна, то відстань в негативному напрямку накопичується.
Це вірно з будь-якою нормою. Наприклад, якщо\(f(t)\) швидкість зміни населення (людини/рік) для міста, то негативні значення вказували\(f\) б на те, що населення міста стає менше, а певним інтегралом (тепер негативним числом) буде зміна чисельності населення, зменшення, протягом часовий інтервал.
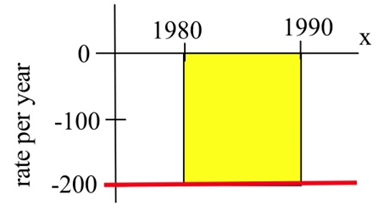
У 1980 році навколо озера гніздяться 12 000 качок, а швидкість зміни популяції (у качок на рік) показана на малюнку нижче. Напишіть певний інтеграл, щоб представити загальну зміну популяції качок з 1980 по 1990 рік та оцініть чисельність населення в 1990 році.
Рішення
Зміна чисельності населення це:\[ \begin{align*} \int\limits_{1980}^{1990} f(t) \,dt & = -(\text{area between \( f \) and axis}) \\ & \approx -(200\text{ ducks/year})\cdot (10\text{ years}) \\ & = -2000\text{ ducks} \end{align*} \nonumber \]
Тоді (популяція качок 1990) = (1980 популяція) + (зміна з 1980 на 1990) = (12 000) + (-2000) = 10000 качок.
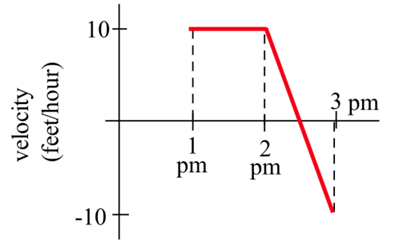
Помилка починається з місця розташування\(x = 12\) на\(x\) -осі о 1 годині вечора йде вздовж осі зі швидкістю,\(v(x)\) показаною на графіку. Як далеко клоп проїжджає між 13:00 і 15:00, і де помилка о 3 годині вечора?
Рішення
Зверніть увагу, що швидкість позитивна з 1 до 2:30, потім стає негативною. Отже, помилка рухається в позитивному напрямку від 1 до 2:30, потім обертається і рухається назад до того місця, де вона почалася. Площа під кривою швидкості від 1 до 2:30 показує загальну відстань, пройдену жуком у позитивному напрямку; помилка перемістилася на 12,5 футів у позитивному напрямку. Площа між кривою швидкості та віссю x, між 2:30 та 3, показує загальну відстань, пройдену жуком у негативному напрямку, назад до будинку; помилка пройшла 2,5 футів у негативному напрямку. Певний інтеграл кривої швидкості\(\int\limits_1^3 v(t) \,dt\), показує чисту зміну відстані:\[\int\limits_1^3 v(t) \,dt = 12.5-2.5=10.\nonumber \]
Помилка виявилася на 10 футів далі в позитивному напрямку, ніж він почав. О 3 годині вечора клоп знаходиться в\(x = 22\).
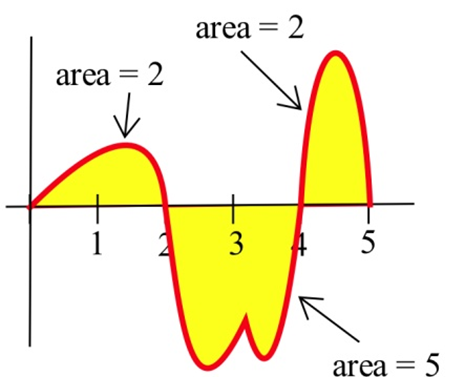
Використовуйте графік нижче, щоб обчислити\( \int\limits_0^2 f(x) \,dx \)\( \int\limits_2^4 f(x) \,dx \),,\( \int\limits_4^5 f(x) \,dx \), і\( \int\limits_0^5 f(x) \,dx \).
Рішення
Використання заданих областей,\( \int\limits_0^2 f(x) \,dx = 2 \),\( \int\limits_2^4 f(x) \,dx = -5 \)\( \int\limits_4^5 f(x) \,dx = 2 \), і\( \int\limits_0^5 f(x) \,dx = \) (область вище)\( - \) (область нижче)\( = (2+2) - (5) = -1\).
Апроксимація з технологією
Якщо ваша функція задана у вигляді графіка або таблиці, вам все одно доведеться наблизити певні інтеграли, використовуючи області, як правило, прямокутників. Але якщо ваша функція дана у вигляді формули, ви можете звернутися до технології, щоб отримати кращу приблизну відповідь. Наприклад, більшість графічних калькуляторів мають якийсь інструмент числового інтеграції вбудований. Ви також можете знайти багато онлайн-інструментів, які можуть це зробити; введіть числову інтеграцію в будь-яку пошукову систему, щоб побачити вибір з них.
Більшість інструментів числового інтегрування використовують прямокутники для оцінки підписаної площі, так само, як і вручну. Але вони використовують набагато більше прямокутників, ніж у вас вистачило б терпіння, тому вони отримують кращу відповідь. Деякі з них використовують системи комп'ютерної алгебри для пошуку точних відповідей; ми дізнаємося, як це зробити самі пізніше в цьому розділі.
Коли ви звернетеся до техніки, щоб знайти значення певного інтеграла, будьте уважні. Далеко не кожен інструмент зможе дати вам правильну відповідь на кожен інтеграл. Спочатку ви повинні скласти оцінку відповіді, щоб ви могли судити, чи має сенс відповідь, яку ви отримаєте.
Використовуйте технологію, щоб наблизити певний інтеграл\( \int\limits_1^5 \frac{1}{x} \,dx \). (Це той самий певний інтеграл, який ми наближали з прямокутниками раніше.)
Рішення
Ми могли б використовувати наступну команду в GeoGebra, щоб наблизити цей інтеграл:
Інтегральна [1/х, 1, 5]
Або натисніть це посилання, щоб побачити, як оцінити цей інтеграл за допомогою Wolfram|Alpha.
Використовуйте технологію, щоб наблизити певний інтеграл\( \int\limits_1^2 e^{x^2+x} \,dx \).
Рішення
Функція тут позитивна, тому тут повинна бути якась область під кривою. Існує не алгебраїчний спосіб знайти точну відповідь, тому деякі програми можуть просто повернути оригінальний інтеграл, а не намагатися наблизити його.
Ми могли б використовувати наступну команду в GeoGebra, щоб наблизити цей інтеграл:
Інтеграл [e^ (х ^ 2+ х), 1, 2]
Або натисніть це посилання, щоб побачити, як наблизити цей інтеграл за допомогою Wolfram|Alpha. Хоча це виглядає як Wolfram|Alpha може оцінити інтеграл, функція Ерфі
, яку вона показує у своїй відповіді, насправді визначається з точки зору іншого інтеграла, тому вона досі не знайшла алгебраїчної відповіді.
Накопичення в реальному житті
Ми вже бачили, що площа
під графіком може представляти величини, одиниці яких не є звичайними геометричними одиницями квадратних метрів або квадратних футів. Наприклад, якщо\(t\) є мірою часу в секундах і\(f(t)\) є швидкістю з одиницями фути/секунду, то певний інтеграл має одиниці (фути/секунди)\( \cdot \) (секунди) = фути.
Загалом, одиницями для певного інтеграла\( \int\limits_a^b f(x)\,dx \) є (\(y\)-одиниці)\( \cdot \) (\(x\)-одиниці). Швидка перевірка агрегатів може допомогти уникнути помилок при налаштуванні застосованої проблеми.
У попередніх прикладах ми розглядали функцію, яка представляла швидкість руху (милі на годину); у цьому випадку площа представляла загальну пройдену відстань. Для функцій, що представляють інші темпи, такі як виробництво заводу (велосипеди на день) або потік води в річці (галони в хвилину) або рух через міст (автомобілі в хвилину), або поширення хвороби (щойно хворі люди на тиждень), площа все одно буде представляти загальну кількість чогось.
\(MR(q)\)Припустимо, граничний дохід в доларах/товар для продажу\(q\) предметів. Що\( \int\limits_0^{150} MR(q) \,dq \) являє собою?
Рішення
\( \int\limits_0^{150} MR(q) \,dq \)має одиниці (долари/елемент)\( \cdot \) (items) = долари, і являє собою накопичені долари для продажу від 0 до 150 предметів. Тобто загальний дохід від продажу 150 найменувань.\( \int\limits_0^{150} MR(q) \,dq = TR(150) \)
Припустимо\(r(t)\), в сантиметрах на рік уявляє, як змінюється діаметр дерева з часом. Що\( \int\limits_{T_1}^{T_2} r(t) \,dt \) являє собою?
Рішення
\( \int\limits_{T_1}^{T_2} r(t) \,dt \)має одиниці (сантиметри на рік)\( \cdot \) (років) = сантиметри, і являє собою накопичений зріст діаметра дерева від\(T_1\) до\(T_2\). \( \int\limits_{T_1}^{T_2} r(t) \,dt \)Тобто відбувається зміна діаметра дерева за цей проміжок часу.
