3.4: Антипохідні формул
- Page ID
- 60263
Тепер ми можемо скласти ідеї областей та антипохідних, щоб отримати спосіб оцінки певних інтегралів, який є точним і часто легким. Щоб оцінити певний інтеграл\( \int\limits_a^b f(t)\, dt \), ми можемо знайти будь-яке антипохідне\(F(t)\)\(f(t)\) і оцінити\(F(b) - F(a)\). Проблема знаходження точного значення певного інтеграла зводиться до знаходження деякого (будь-якого)\(F\) антипохідного цілого і подальшої оцінки\(F(b) - F(a)\). Навіть знайти одне антидериватив може бути важко, і ми будемо дотримуватися функцій, які мають легкі антипохідні.
Будівельні блоки
Антидиференціація йде назад через похідний процес. Отже, найпростіші антидеривативні правила - це просто зворотні версії найпростіших похідних правил. Нагадаємо з глави 2:
У чому випливає,\(f\) і\(g\) диференційовані функції\(x\).
Постійне множинне правило
\[ \frac{d}{dx}\left( kf\right)=kf'\nonumber \]
Правило суми та різниці
\[\frac{d}{dx}\left(f\pm g\right)=f' \pm g'\nonumber \]
Правило влади
\[\frac{d}{dx}\left(x^n\right)=nx^{n-1}\nonumber \]
Особливі випадки:\[\frac{d}{dx}\left(k\right)=0 \quad \text{(Because \( k=kx^0 \).)}\nonumber \]\[\frac{d}{dx}\left(x\right)=1 \quad \text{(Because \( x=x^1 \).)}\nonumber \]
Експоненціальні функції
\[\frac{d}{dx}\left(e^x\right)=e^x\nonumber \]\[\frac{d}{dx}\left(a^x\right)=\ln(a)\,a^x\nonumber \]
Натуральний логарифм
\[\frac{d}{dx}\left(\ln(x)\right)=\frac{1}{x}\nonumber \]
Думати над цими основними правилами було те, як ми придумали антипохідні\(2x\) і\( e^x \) раніше.
Відповідні правила для антипохідних наступні — кожне з антидеривативних правил просто переписує похідне правило. Всі ці антипохідні можна перевірити шляхом диференціації.
Є одна несподіванка —\(\frac{1}{x}\) антипохідне насправді не просто\(\ln(x)\), це\(\ln|x|\). Це добре - антидериватив має домен, який відповідає домену\(\frac{1}{x}\), який більше, ніж домен\(\ln(x)\), тому нам не доведеться турбуватися про те, чи є наші\(x\) позитивні чи негативні. Але ми повинні бути обережними, щоб включити ці абсолютні значення - інакше ми могли б закінчитися проблемами домену.
У чому випливає,\(f\) і\(g\) знаходяться диференційовані функції\(x\)\( k \), і\( n \), і\( C \) є константами.
Постійне множинне правило
\[ \int k\cdot f(x)\, dx=k\cdot\int f(x)\, dx\nonumber \]
Правило суми та різниці
\[\int \left(f(x)\pm g(x)\right)\, dx=\int f(x)\, dx \pm \int g(x)\, dx\nonumber \]
Правило влади
\[ \int x^n \, dx = \frac{x^{n+1}}{n+1}+C, \text{ provided that } n\neq -1\nonumber \]
Особливий випадок:\[ \int k\, dx =kx+C \quad \text{(Because \( k=kx^0 \).)}\nonumber \] (Інший спеціальний випадок (\( n=-1 \)) охоплюється далі.)
Натуральний логарифм
\[\int x^{-1}\, dx =\int\frac{1}{x}\, dx = \ln|x|+C\nonumber \]
Експоненціальні функції
\[ \int e^x\, dx=e^x +C \nonumber \]\[ \int a^x\, dx = \frac{a^x}{\ln(a)}+C \nonumber \]
Знайдіть антипохідне від\( y=3x^7-15\sqrt{x}+\frac{14}{x^2} \).
Рішення
\[ \begin{align*} \int\left( 3x^7-15\sqrt{x}+\frac{14}{x^2} \right)\, dx & = \int\left( 3x^7-15x^{1/2}+14x^{-2} \right)\, dx \\ & = 3\frac{x^8}{8}-15\frac{x^{3/2}}{3/2}+14\frac{x^{-1}}{-1}+C \\ & = \frac{3}{8}x^8-10x^{3/2}-14x^{-1}+C \end{align*} \nonumber \]
Знайти\( \int\left(e^x+12-\frac{16}{x}\right)\, dx \).
Рішення
\[ \int\left(e^x+12-\frac{16}{x}\right)\, dx =e^x+12x-16\ln|x|+C\nonumber \]
Знайти\(F(x)\) так, щоб\( F'(x)=e^x \) і\( F(0)=10 \).
Рішення
Цього разу ми шукаємо певну антипохідну; нам потрібно знайти саме потрібну константу. Почнемо з пошуку антидериватива:\[ \int e^x\, dx=e^x+C \nonumber \]
Отже, ми знаємо\( F(x)=e^x+\text{(some constant)} \), що, тепер нам просто потрібно знайти, який з них. Для цього ми використаємо іншу частину інформації (початкова умова):\[ \begin{align*} F(x) & = e^x+C \\ F(0) & = e^0+C=1+C=10 \\ C & = 9 \end{align*} \nonumber \]
Особлива константа, яка нам потрібна, - 9; таким чином,\( F(x)=e^x+9 \).
Причина, по якій ми зараз дивимося на антипохідні, полягає в тому, щоб ми могли точно оцінити певні інтеграли. Нагадаємо фундаментальну теорему числення:
Якщо\(F(x)\) є функцією де\(F'(x) = f(x)\), то
\[ \int\limits_a^b f(x)\, dx = F(b)-F(a) \nonumber \]
Якщо ми можемо знайти антипохідне для integrand, ми можемо використовувати це для оцінки певного інтеграла. Оцінка\(F(b) - F(a)\) представлена у вигляді\( \left.F(x)\right]_a^b \) або\( \left.F(x)\right|_a^b \).
\( \int\limits_1^3 x\, dx \)Оцінювати можна двома способами:
- Шляхом замальовки графіка\(y = x\) і геометрично знаходячи площу.
- За допомогою знаходження антидериватива\(F(x)\) цілісного і оцінюючи\(F(3)-F(1)\).
Рішення
- Графік\(y = x \) показаний нижче, а затінена область, що відповідає інтегралу, має площу 4.
- Одне\(x\) антипохідне є\( F(x)=\frac{1}{2}x^2 \), і\[ \begin{align*} \int\limits_1^3 x\, dx & = \left[\frac{1}{2}x^2\right]_1^3 \\ & = \left(\frac{1}{2}(3)^2\right) - \left(\frac{1}{2}(1)^2\right) \\ & = \frac{9}{2}-\frac{1}{2} \\ & = 4. \end{align*} \nonumber \] Зверніть увагу, що ця відповідь узгоджується з відповіддю, яку ми отримали геометрично.
Якщо ми використовували інше антипохідне від х, скажімо\( F(x)=\frac{1}{2}x^2+7 \), то\[ \begin{align*} \int\limits_1^3 x\, dx & = \left[\frac{1}{2}x^2+7\right]_1^3 \\ & = \left(\frac{1}{2}(3)^2+7\right) - \left(\frac{1}{2}(1)^2+7\right) \\ & = \frac{9}{2}+7-\frac{1}{2}-7 \\ & = 4. \end{align*} \nonumber \]
Загалом, незалежно від константи, яку ми вибираємо, віднімається під час оцінки, тому ми могли б також завжди вибрати найпростіший, де константа дорівнює 0.
Знайдіть площу між графіком\(y = 3x^2\) і горизонтальною віссю для\(x\) між 1 і 2.
Рішення
Це\[ \int\limits_1^2 3x^2\, dx = \left.x^3\right|_1^2 = 2^3-1^3 = 7. \nonumber \]
Робот був запрограмований так, що коли він почне рухатися, його швидкість через\(t\) секунди становитиме\( 3t^2 \) фути/секунду.
- Як далеко проїде робот протягом перших 4 секунд руху?
- Як далеко робот проїде протягом наступних 4 секунд руху?
Рішення
- Відстань протягом перших 4 секунд буде областю під графіком швидкості, від\(t = 0\) до\(t = 4\).
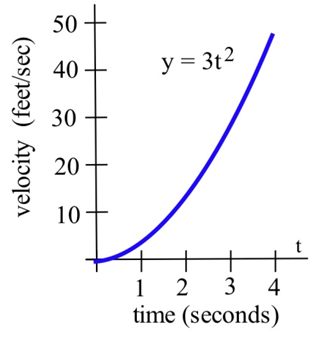
Ця область є певним інтегралом\( \int\limits_0^4 3t^2\, dt \). Антипохідне від\( 3t^2 \) є\( t^3 \), так\( \int\limits_0^4 3t^2\, dt =\left. t^3 \right]_0^4 =4^3-0^3 = 64\) ноги.
- \( \int\limits_4^8 3t^2\, dt =\left. t^3 \right]_4^8=8^3-4^3 =512 - 64 = 448\)стопи.
Припустимо, що через\(t\) хвилини після покладання 1000 бактерій на тарілку Петрі швидкість росту популяції становить\(6t\) бактерії в хвилину.
- Скільки нових бактерій додається в популяцію протягом перших 7 хвилин?
- Яка загальна чисельність населення через 7 хвилин?
Рішення
- Кількість нових бактерій - це площа під графіком швидкості росту, а одна антипохідна\(6t\) - це\(3t^2\).
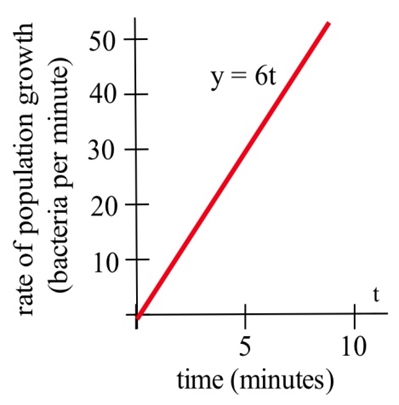
Так\[\text{new bacteria}=\int\limits_0^7 6t\, dt= \left. 3t^2\right|_0^7=3(7)^2-3(0)^2=147\nonumber \]
- Нова популяція = (стара популяція) + (нові бактерії) = 1000 + 147 = 1147 бактерій.
Компанія визначає їх граничні витрати на виробництво, в доларах за одиницю, є\( MC(x)=\frac{4}{\sqrt{x}}+2 \) при виробництві\(x\) тисячі найменувань. Знайдіть витрати на збільшення виробництва з 4 тисяч найменувань до 5 тисяч найменувань.
Рішення
Пам'ятайте, що гранична вартість - це швидкість зміни вартості, і тому фундаментальна теорема говорить нам про це\( \int\limits_a^b MC(x)\, dx = \int\limits_a^b C'(x)\, dx = C(b)-C(a) \). Іншими словами, інтеграл граничної вартості дасть нам чисту зміну вартості. Щоб знайти вартість збільшення виробництва з 4 тис. найменувань до 5 тисяч найменувань, нам потрібно інтегрувати\( \int\limits_4^5 MC(x)\, dx\).
Ми можемо написати граничну вартість як\( MC(x)=4x^{-1/2}+2 \). Потім ми можемо використовувати основні правила, щоб знайти антидериватив:\[ C(x)=4\frac{x^{1/2}}{1/2}+2x=8\sqrt{x}+2x.\nonumber \]
Використовуючи це,\[ \begin{align*} \text{Net change in cost } & = \int\limits_4^5 \left(4x^{-1/2}+2\right)\, dx \\ & = \left[ 8\sqrt{x}+2x \right]_4^5 \\ & = \left( 8\sqrt{5}+2(5) \right)-\left( 8\sqrt{4}+2(4) \right) \\ & \approx 3.889 \end{align*} \nonumber \]
Це обійдеться в 3,889 тисячі доларів, щоб збільшити виробництво з 4 тисяч найменувань до 5 тисяч найменувань. (Остаточна відповідь буде краще написана як $3889.)
