3.1: Прелюдія до інтеграла

Last updated
Save as PDF

Page ID: 60273

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Попередні глави стосувалися диференціального числення. Ми почали з простого геометричного уявлення про нахил дотичної лінії до кривої, розвинули її в комбінацію теорії про похідні та їх властивості, методів обчислення похідних та застосувань похідних. У цій главі розглядається інтегральне числення і починається з простої геометричної ідеї площі. Ця ідея буде розвинена в іншу комбінацію теорії, прийомів і додатків.

Ідея попереднього обчислення - Площа прямокутника

Якщо ви подивитеся на внутрішню обкладинку майже будь-якої традиційної математичної книги, ви знайдете купу формул площі та об'єму — площа квадрата, площа трапеції, об'єм правого кругового конуса тощо. Деякі з цих формул досить складні. Але ви все одно не знайдете формулу для площі шматочка головоломки або об'єму яйця. Є багато речей, для яких немає формули. Тим не менш, ми все ще можемо захотіти знайти їх області.

Одна з причин, чому області настільки корисні, полягає в тому, що вони можуть представляти величини, відмінні від простих геометричних фігур. Якщо одиницями для кожної сторони прямокутника є метри, то площа матиме одиниці\(meters \cdot meters = square \ meters = \text{m}^2\). Але якщо одиницями основи прямокутника є години, а одиниці висоти - милі/годину, то одиниці площі прямокутника є\(hours \cdot (miles/hour) = miles\) мірою відстані. Аналогічно, якщо базовими одиницями є сантиметри, а одиниці висоти - грами, то одиниці площі - грам-сантиметри, міра роботи.

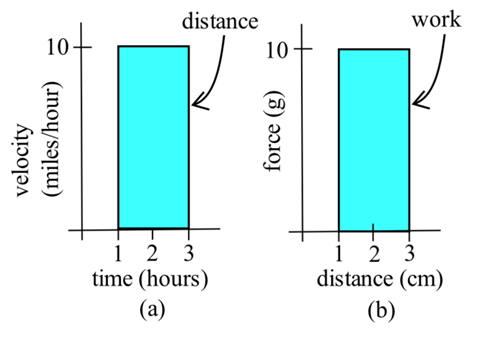
Основна форма, яку ми будемо використовувати, - це прямокутник; площа прямокутника - це\( \cdot \) висота основи. Ви також повинні знати формули площі для трикутників\( A=\frac{1}{2}bh \), і для кіл,\( A=\pi r^2 \).