16.9: Глава 16 Огляд вправ

Last updated

Oct 27, 2022
Save as PDF
- 16.8E: Вправи для розділу 16.8
- 17: Диференціальні рівняння другого порядку

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Правда чи брехня? Обгрунтуйте свою відповідь доказом або контрприкладом.

1. $\vecs F(x,y) = x^2 y\,\mathbf{\hat i} + y^2 x\,\mathbf{\hat j}$ Векторне поле консервативне.

Відповідь: Помилковий

2. Для векторного поля $\vecs F(x,y) = P(x,y)\,\mathbf{\hat i} + Q(x,y)\,\mathbf{\hat j}$ , якщо $P_y(x,y) = Q_z(x,y)$ у відкритому регіоні $D$ , то $\displaystyle \int_{\partial D} P \,dx + Q \, dy = 0.$

3. Розбіжність векторного поля є векторним полем.

Відповідь: Помилковий

4. Якщо $curl \, \vecs F = \vecs 0$ , то $\vecs F$ є консервативним векторним полем.

Намалюйте наступні векторні поля.

5. $\vecs F(x,y) = \dfrac{1}{2}\,\mathbf{\hat i} + 2x\,\mathbf{\hat j}$

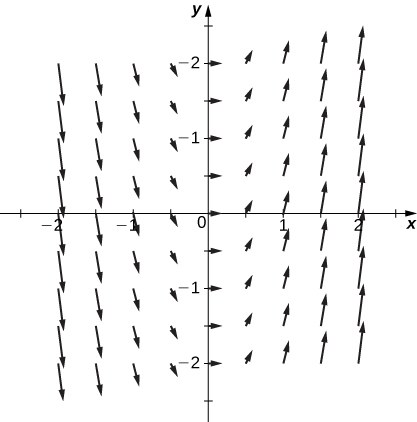
Відповідь: $Векторне поле у двох вимірах. Всі квадранти показані. Стрілки тим більше, чим далі від осі y вони стають. Вони вказують вгору і вправо для позитивних значень x і вниз і праворуч для від'ємних значень x. Чим далі від осі y вони знаходяться, тим крутіше нахил у них.$

Template:ContribOpenStaxCalc