16.7: Теорема Стокса

Цілі навчання

• Поясніть значення теореми Стокса.
• Використовуйте теорему Стокса для оцінки лінійного інтеграла.
• Використовуйте теорему Стокса для обчислення поверхневого інтеграла.
• Використовуйте теорему Стокса для обчислення завитка.

У цьому розділі ми вивчаємо теорему Стокса, більш вимірне узагальнення теореми Гріна. Ця теорема, як фундаментальна теорема для лінійних інтегралів та теорема Гріна, є узагальненням фундаментальної теореми числення до вищих вимірів. Теорема Стокса пов'язує векторний інтеграл поверхні над поверхнею$S$ у просторі з лінійним інтегралом навколо кордону$S$. Тому так само, як теореми перед ним, теорема Стокса може бути використана для зведення інтеграла над геометричним об'єктом$S$ до інтеграла через межу$S$. Окрім того, що дозволяє нам перекладати між лінійними інтегралами та поверхневими інтегралами, теорема Стокса з'єднує поняття завитка та циркуляції. Крім того, теорема має застосування в механіці рідини та електромагнетизмі. Ми використовуємо теорему Стокса для отримання закону Фарадея, важливого результату за участю електричних полів.

Теорема Стокса

Теорема Стокса говорить, що ми можемо обчислити потік$curl \,\vecs{F}$ по всій поверхні$S$, знаючи інформацію тільки про значення$\vecs{F}$ вздовж кордону$S$. І навпаки, ми можемо обчислити лінійний інтеграл векторного поля$\vecs{F}$ вздовж межі поверхні$S$ шляхом перекладу в подвійний інтеграл завитка$\vecs{F}$ над$S$.

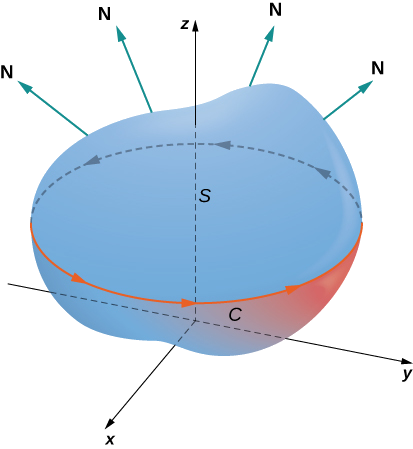
$S$Дозволяти орієнтовану гладку поверхню з одиничним нормальним вектором$\vecs{N}$. Крім того, припустимо, що межа$S$ є простою замкнутою кривою$C$. Орієнтація$S$ індукує позитивну орієнтацію,$C$ якщо, коли ви ходите в позитивному напрямку навколо$C$ з головою, спрямованою у напрямку$\vecs{N}$, поверхня завжди знаходиться зліва від вас. Маючи це визначення на місці, ми можемо констатувати теорему Стокса.

Теорема$\PageIndex{1}$: Stokes’ Theorem

$S$Дозволяти бути кусково гладкою орієнтованою поверхнею з межею, яка є простою замкнутою кривою$C$ з позитивною орієнтацією (рис.$\PageIndex{1}$). Якщо$\vecs{F}$ векторне поле з компонентними функціями, які мають неперервні часткові похідні на відкритій області$S$, що містять, то

$$\int_C \vecs{F} \cdot d \vecs{r} = \iint_S curl \, \vecs{F} \cdot d\vecs S. \label{Stokes1}$$

Рисунок$\PageIndex{1}$: Теорема Стокса пов'язує інтеграл потоку над поверхнею з лінійним інтегралом навколо межі поверхні. Зверніть увагу, що орієнтація кривої позитивна.

Припустимо$S$, поверхня - це плоска область в$xy$ -площині з орієнтацією вгору. Тоді одиничним нормальним вектором є$\vecs{k}$ і поверхневий інтеграл

$$\iint_S curl \, \vecs{F} \cdot d\vecs{S} \nonumber$$

насправді є подвійним інтегралом

$$\iint_S curl \, \vecs{F} \cdot \vecs{k} \, dA. \nonumber$$

У цьому особливому випадку теорема Стокса дає

$$\int_C \vecs{F} \cdot d\vecs{r} = \iint_S curl \, \vecs{F} \cdot \vecs{k} \, dA. \nonumber$$

Однак це форма потоку теореми Гріна, яка показує нам, що теорема Гріна є окремим випадком теореми Стокса. Теорема Гріна може обробляти тільки поверхні в площині, але теорема Стокса може обробляти поверхні в площині або в просторі.

Повне доказ теореми Стокса виходить за рамки цього тексту. Ми дивимося на інтуїтивне пояснення істинності теореми, а потім бачимо доказ теореми в особливому випадку, що поверхня$S$ є частиною графіка функції$S$, і, межі$S$, і всі$\vecs{F}$ вони досить ручні.

Доказ

Спочатку розглянемо неформальне доказ теореми. Цей доказ не є суворим, але він покликаний дати загальне відчуття того, чому теорема вірна. $S$Дозволяти бути поверхнею і нехай$D$ буде невеликий шматок поверхні так, що$D$ не поділяють жодних точок з межею$S$. Ми вибираємо$D$, щоб бути досить маленьким, щоб його можна було наблизити орієнтованим квадратом$E$. Нехай$D$ успадковує його орієнтацію від$S$, і дати таку$E$ ж орієнтацію. Цей квадрат має чотири сторони; позначають їх$E_l, \, E_r, \, E_u$, а$E_d$ для лівої, правої, вгору і вниз сторін відповідно. На квадраті ми можемо використовувати форму потоку теореми Гріна:

$$\int_{E_l+E_d+E_r+E_u} \vecs{F} \cdot d \vecs{r} = \iint_E curl \, \vecs{F} \cdot \vecs{N} \, d \vecs{S} = \iint_E curl \, \vecs{F} \cdot d\vecs{S}. \nonumber$$

Для наближення потоку по всій поверхні складаємо значення флюсу на малих квадратах, що наближають дрібні шматочки поверхні (рис.$\PageIndex{2}$).

Малюнок$\PageIndex{2}$: Подрібніть поверхню на дрібні шматочки. Шматочки повинні бути досить маленькими, щоб їх можна було наблизити квадратом.

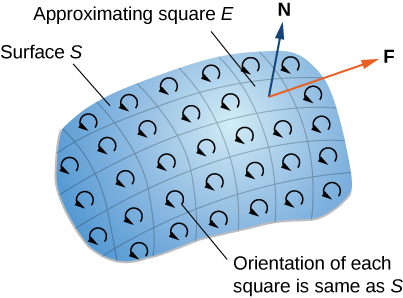
За теоремою Гріна потік через кожен наближений квадрат є лінійним інтегралом над його межею. $F$Дозволяти бути наближений квадрат з орієнтацією, успадкованою від$S$ і з правого боку$E_l$ (так$F$ знаходиться зліва від$E$). Нехай$F_r$ позначають праву сторону$F$; потім,$E_l = - F_r$. Іншими словами, права сторона$F$ - це та ж крива, що і ліва сторона$E$, просто орієнтована в протилежному напрямку. Тому,

$$\int_{E_l} \vecs F \cdot d\vecs r = - \int_{F_r} \vecs F \cdot d\vecs r. \nonumber$$

Коли ми складаємо всі потоки по всіх квадратах, апроксимуючи поверхню$S$, лінійні інтеграли

$$\int_{E_l} \vecs{F} \cdot d \vecs{r} \nonumber$$

і

$$\int_{F_r} \vecs{F} \cdot d\vecs{r} \nonumber$$

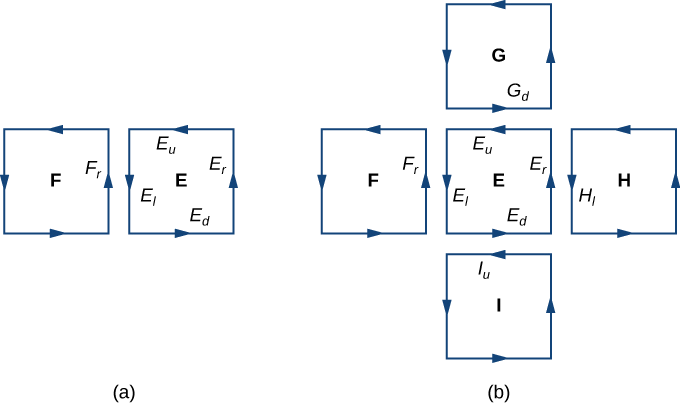
скасувати один одного. Те ж саме стосується лінійних інтегралів над іншими трьома сторонами$E$. Ці три лінійні інтеграли скасовуються з лінійним інтегралом нижньої сторони квадрата вище$E$, лінійним інтегралом над лівою стороною квадрата праворуч та лінійним інтегралом над верхньою стороною квадрата нижче$E$ (рис.$\PageIndex{3}$).$E$ Після того, як все це скасування відбувається над усіма апроксимуючими квадратами, єдиними лінійними інтегралами, які виживають, є лінійні інтеграли по сторонам, що наближають межу$S$. Отже, сума всіх потоків (яка, за теоремою Гріна, є сумою всіх лінійних інтегралів навколо кордонів наближених квадратів) може бути наближена прямим інтегралом через межу$S$. У межі, коли площі наближених квадратів йдуть до нуля, це наближення довільно наближається до потоку.

Малюнок$\PageIndex{3}$: (а) Лінійний інтеграл вздовж$E_l$ скасовує інтеграл лінії вздовж$F_r$ тому, що$E_l = - F_r$. (b) Лінійний інтеграл уздовж будь-якої зі сторін$E$ скасовується з лінійним інтегралом уздовж сторони сусіднього наближення квадрата.

Давайте тепер розглянемо суворе доказ теореми в особливому випадку, що$S$ є графіком функції$z = f(x,y)$, де$x$ і$y$ варіюються над обмеженою, просто пов'язаною областю$D$ скінченної площі (рис.$\PageIndex{4}$). Крім того, припустимо, що$f$ має неперервні часткові похідні другого порядку. Нехай$C$ позначають межу$S$ і нехай$C'$ позначають межу$D$. Потім,$D$ є «тінь»$S$ в площині і$C'$ є «тінню»$C$. Припустимо,$S$ що орієнтована вгору. Орієнтація проти годинникової стрілки позитивна, як і орієнтація проти годинникової стрілки$C'$.$C$ $\vecs F(x,y,z) = \langle P,Q,R \rangle$Дозволяти векторне поле з компонентними функціями, які мають неперервні часткові похідні.

Малюнок$\PageIndex{4}$:$D$ є «тінь», або проекція,$S$ в площині і$C'$ є проекцією$C$.

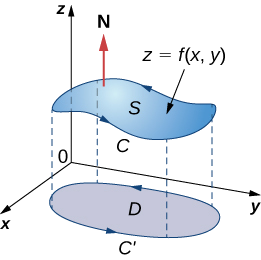
Беремо стандартну параметризацію$S \, : \, x = x, \, y = y, \, z = g(x,y)$. Дотичні вектори є$\vecs t_x = \langle 1,0,g_x \rangle$ і$\vecs t_y = \langle 0,1,g_y \rangle$, і тому$\vecs t_x \times \vecs t_y = \langle -g_x, \, -g_y, \, 1 \rangle$.

$$\iint_S curl \, \vecs{F} \cdot d\vecs{S} = \iint_D [- (R_y - Q_z)z_x - (P_z - R_x)z_y + (Q_x - P_y)] \, dA, \nonumber$$

де часткові похідні оцінюються на$(x,y,g(x,y))$, що робить ціле залежне від$x$ і$y$ тільки. $\langle x (t), \, y(t) \rangle, \, a \leq t \leq b$Припустимо, це параметризація$C'$. Потім проводиться параметризація$C$ іс$\langle x (t), \, y(t), \, g(x(t), \, y(t))\rangle, \, a \leq t \leq b$. Озброївшись цими параметризаціями, правилом Ланцюга та теоремою Гріна, і маючи на увазі$P$, що$Q$ і$R$ всі функції$x$ і$y$, ми можемо оцінити лінійний інтеграл

$$\begin{align*} \int_C \vecs{F} \cdot d \vecs{r} &= \int_a^b (Px'(t) + Qy'(t) + Rz'(t)) \, dt \\[4pt] &= \int_a^b \left[Px'(t) + Qy'(t) + R\left(\dfrac{\partial z}{\partial x} \dfrac{dx}{dt} + \dfrac{\partial z}{\partial y} \dfrac{dy}{dt}\right) \right] dt \\[4pt] &= \int_a^b \left[ \left(P + R \dfrac{\partial z}{\partial x} \right) x' (t) + \left(Q + R \dfrac{\partial z}{\partial y} \right) y'(t) \right] dt \\[4pt] &= \int_{C'} \left(P + R \dfrac{\partial z}{\partial x} \right)\, dx + \left(Q + R \dfrac{\partial z}{\partial y} \right) \, dy \\[4pt] &= \iint_D \left[ \dfrac{\partial}{\partial x} \left( Q + R \dfrac{\partial z}{\partial y} \right) - \dfrac{\partial}{\partial y} \left(P + R \dfrac{\partial z}{\partial x} \right) \right] \, dA \\[4pt] &=\iint_D \left(\dfrac{\partial Q}{\partial x} + \dfrac{\partial Q}{\partial z} \dfrac{\partial z}{\partial x} + \dfrac{\partial R}{\partial x} \dfrac{\partial z}{\partial y} + \dfrac{\partial R}{\partial z}\dfrac{\partial z}{\partial x} \dfrac{\partial z}{\partial y} + R \dfrac{\partial^2 z}{\partial x \partial y} \right) - \left(\dfrac{\partial P}{\partial y} + \dfrac{\partial P}{\partial z} \dfrac{\partial z}{\partial y} + \dfrac{\partial R}{\partial z} \dfrac{\partial z}{\partial y} \dfrac{\partial z}{\partial x} + R \dfrac{\partial^2 z}{\partial y \partial x} \right) \end{align*} \nonumber$$

За теоремою Клеро,

$$\dfrac{\partial^2 z}{\partial x \partial y} = \dfrac{\partial^2 z}{\partial y \partial x} \nonumber$$

Тому чотири терміни зникають з цього подвійного інтеграла, і ми залишаємося з

$$\iint_D [- (R_y - Q_z)Z_x - (P_z - R_x) z_y + (Q_x - P_y)] \, dA, \nonumber$$

який дорівнює

$$\iint_S curl \, \vecs{F} \cdot d\vecs{S}. \nonumber$$

$\Box$

Показано, що теорема Стокса є істинною у випадку функції з областю, яка є просто зв'язаною областю скінченної площі. Ми можемо швидко підтвердити цю теорему для іншого важливого випадку: коли$\vecs{F}$ векторне поле є консервативним полем. Якщо$\vecs{F}$ консервативний, то локон$\vecs{F}$ дорівнює нулю, тому

$$\iint_S curl \, \vecs{F} \cdot d\vecs{S} = 0. \nonumber$$

Оскільки межа$S$ - замкнута крива, інтеграл

$$\int_C \vecs{F} \cdot d\vecs{r}. \nonumber$$

також дорівнює нулю.

Приклад$\PageIndex{1}$: Verifying Stokes’ Theorem for a Specific Case

Переконайтеся, що теорема Стокса вірна для векторного поля$\vecs{F}(x,y) = \langle -z,x,0 \rangle$ та поверхні$S$, де$S$ є півкуля, орієнтована назовні, з параметризацією,$\vecs r(\phi, \theta) = \langle \sin \phi \, \cos \theta, \, \sin \phi \, \sin \theta, \, \cos \phi \rangle, \, 0 \leq \theta \leq \pi, \, 0 \leq \phi \leq \pi$ як показано на малюнку$\PageIndex{5}$.

Рисунок$\PageIndex{5}$: Перевірка теореми Стокса для півкулі в векторному полі.

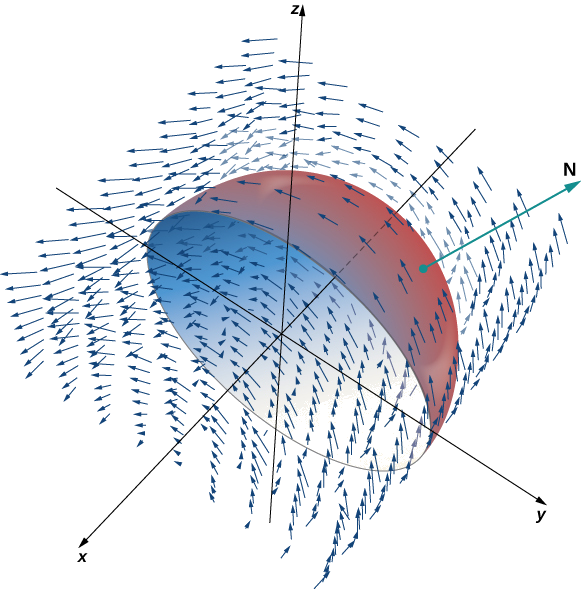
Рішення

$C$Дозволяти межа$S$. Зверніть увагу, що$C$ це коло радіусом 1, центрований у початковій точці, що сидить у площині$y = 0$. Це коло має параметризацію$\langle \cos t, \, 0, \, \sin t \rangle, \, 0 \leq t \leq 2\pi$. Рівняння для скалярних поверхневих інтегралів

$$\begin{align*} \int_C \vecs{F} \cdot d \vecs{r} &= \int_0^{2\pi} \langle -\sin t, \, \cos t, \, 0 \rangle \cdot \langle - \sin t, \, 0, \, \cos t \rangle \, dt \\[4pt] &= \int_0^{2\pi} \sin^2 t \, dt \\[4pt] &= \pi. \end{align*}$$

За рівнянням для векторних лінійних інтегралів,

$$\begin{align*} \iint_S \, curl \, \vecs{F} \cdot d\vecs S &= \iint_D curl \, \vecs{F} (\vecs r (\phi,\theta)) \cdot ( \vecs t_{\phi} \times \vecs t_{\theta}) \, dA \\[4pt] &= \iint_D \langle 0, -1, 1 \rangle \cdot \langle \cos \theta \, \sin^2 \phi, \, \sin \theta \, \sin^2 \phi, \, \sin \phi \, \cos \phi \rangle \, dA \\[4pt] &= \int_0^{\pi} \int_0^{\pi} (\sin \phi \, \cos \phi - \sin \theta \, \sin^2 \phi ) \, d\phi d\theta \\[4pt] &= \dfrac{\pi}{2} \int_0^{\pi} \sin \theta \, d\theta \\[4pt] &= \pi.\end{align*}$$

Тому ми перевірили теорему Стокса для цього прикладу.

Вправа$\PageIndex{1}$

Переконайтеся, що теорема Стокса вірна для векторного поля$\vecs{F}(x,y,z) = \langle y,x,-z \rangle$ та поверхні$S$, де$S$ знаходиться орієнтована вгору частина графа$f(x,y) = x^2 y$ над трикутником у$xy$ -площині з вершинами$(0,0), \, (2,0)$, і$(0,2)$.

Підказка

Розрахуйте подвійний інтеграл і лінійний інтеграл окремо.

Відповідь

Обидва інтеграли дають$-\dfrac{136}{45}$:

Застосування теореми Стокса

Теорема Стокса перекладається між інтегралом потоку поверхні$S$ до прямої інтегральної навколо кордону$S$. Тому теорема дозволяє обчислити поверхневі інтеграли або лінійні інтеграли, що зазвичай було б досить складно шляхом перекладу лінійного інтеграла в поверхневий інтеграл або навпаки. Зараз ми вивчимо кілька прикладів кожного виду перекладу.

Приклад$\PageIndex{2}$: Calculating a Surface Integral

Обчислити інтеграл поверхні

$$\iint_S curl \, \vecs{F} \cdot d\vecs S, \nonumber$$

де$S$ - поверхня, орієнтована назовні, на малюнку$\PageIndex{6}$ і$\vecs{F} = \langle z,\, 2xy, \, x + y \rangle$.

Малюнок$\PageIndex{6}$: Складна поверхня у векторному полі.

Рішення

Зверніть увагу, що для розрахунку

$$\iint_S curl \, \vecs F \cdot d\vecs S \nonumber$$

без використання теореми Стокса нам знадобиться рівняння для скалярних поверхневих інтегралів. Використання цього рівняння вимагає параметризації$S$. Поверхня$S$ досить складна, що знайти параметризацію було б вкрай складно. Тому методи, які ми вивчили в попередніх розділах, не корисні для цієї проблеми. Замість цього ми використовуємо теорему Стокса, зазначивши, що$C$ межа поверхні є лише єдиним колом з радіусом 1.

Завиток$\vecs{F}$ є$\langle 1,1,2y \rangle$. За теоремою Стокса,

$$\iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r, \nonumber$$

де$C$ має параметризацію$\langle \cos t, \, \sin t, \, 1 \rangle, 0 \leq t \leq 2\pi$. За рівнянням для векторних лінійних інтегралів,

$$\begin{align*} \iint_S curl \, F \cdot d\vecs S &= \int_C \vecs{F} \cdot d \vecs{r} \\[4pt] &= \int_0^2 \langle 1, \, \sin t \, \cos t, \, \cos t + \sin t \rangle \cdot \langle - \sin t, \, \cos t, \, 0 \rangle \, dt \\[4pt] &= \int_0^{2\pi} ( - \sin t + 2 \, \sin t \, \cos^2 t ) \, dt \\[4pt] &= \left[ \cos t - \dfrac{2 \, \cos^3 t}{3} \right]_0^{2\pi} \\[4pt] &= \cos (2\pi) - \dfrac{2 \, \cos^3 (2\pi)}{3} - \left(\cos (0) - \dfrac{2 \, \cos^3 (0)}{3} \right) \\[4pt] &= 0. \end{align*} \nonumber$$

Дивовижний наслідок теореми Стокса полягає в тому, що якщо$S'$ будь-яка інша гладка поверхня з межею$C$ і такою ж орієнтацією$S$, як, то $$\iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r = 0 \nonumber$$ тому, що теорема Стокса говорить, що поверхневий інтеграл залежить тільки від лінійного інтеграла навколо кордону.

У прикладі$\PageIndex{2}$ ми обчислили поверхневий інтеграл просто за допомогою інформації про межу поверхні. Загалом, нехай$S_1$ і$S_2$ будуть гладкі поверхні з однаковою межею$C$ і однаковою орієнтацією. За теоремою Стокса,

$$\iint_{S_1} curl \, \vecs{F} \cdot d\vecs{S} = \int_C \vecs{F} \cdot d\vecs{r} = \iint_{S_2} curl \, \vecs{F} \cdot d\vecs{S}. \label{20}$$

Тому, якщо

$$\iint_{S_1} curl \, \vecs{F} \cdot d\vecs{S} \nonumber$$

важко обчислити, але

$$\iint_{S_2} curl \, \vecs{F} \cdot d\vecs S \nonumber$$

легко обчислити, теорема Стокса дозволяє обчислити більш легкий поверхневий інтеграл. У$\PageIndex{2}$ прикладі ми могли б обчислити

$$\iint_S curl \, \vecs{F} \cdot d \vecs{S} \nonumber$$

шляхом розрахунку

$$\iint_{S'} curl \, \vecs{F} \cdot d\vecs{S}, \nonumber$$

де$\vecs{S}'$ - диск, укладений граничною кривою$C$ (набагато простіша поверхня, з якою можна працювати).

Рівняння\ ref {20} показує, що інтеграли потоку векторних полів завитків незалежні від поверхні так само, як лінійні інтеграли градієнтних полів не залежать від шляху. Нагадаємо,$\vecs{F}$ що якщо двовимірне консервативне векторне поле, визначене на просто пов'язаній області,$f$ є потенційною функцією для$\vecs{F}$, і$C$ є кривою в області$\vecs{F}$, то

$$\int_C \vecs{F} \cdot d\vecs{r} \nonumber$$

залежить тільки від кінцевих точок$C$. Тому якщо будь-яка$C'$ інша крива з тією ж початковою точкою і кінцевою точкою, що і$C$ (тобто$C'$ має ту ж орієнтацію, що і$C$), то

$$\int_C \vecs{F} \cdot d\vecs{r} = \int_{C'} \vecs{F} \cdot d\vecs{r} \nonumber$$

Іншими словами, значення інтеграла залежить тільки від межі шляху; воно насправді не залежить від самого шляху.

Аналогічно, припустимо, що$S$ і$S'$ є поверхнями з однаковою межею і однаковою орієнтацією, і припустимо, що$\vecs{G}$ це тривимірне векторне поле, яке можна записати як завиток іншого векторного поля$\vecs{F}$ (так що$\vecs{F}$ це як «потенційне поле»$\vecs{G}$). За рівнянням\ ref {20},

$$\begin{align*} \iint_S \vecs G \cdot d\vecs S = \iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r = \iint_{S'} curl \, \vecs F \cdot d\vecs S = \iint_{S'} \vecs G \cdot d\vecs S.\end{align*} \nonumber$$

Тому інтеграл потоку$\vecs{G}$ не залежить від поверхні, тільки від кордону поверхні. Інтеграли потоку векторних полів, які можна записати як завиток векторного поля, незалежні від поверхні так само, як лінійні інтеграли векторних полів, які можна записати як градієнт скалярної функції, не залежать від шляху.

Вправа$\PageIndex{1}$

Використовуйте теорему Стокса для обчислення інтеграла поверхні, $$\iint_S curl \, \vecs{F} \cdot d\vecs{S}, \nonumber$$ де$\vecs{F} = \langle x,y,z \rangle$ і$S$ є поверхнею, як показано на наступному малюнку.

Підказка

Параметризувати межу$S$ and translate to a line integral.

Answer

$-\pi$

Example $\PageIndex{3}$: Calculating a Line Integral

Calculate the line integral

$$\int_C \vecs{F} \cdot d\vecs{r}, \nonumber$$

where $\vecs{F} = \langle xy, \, x^2 + y^2 + z^2, \, yz \rangle$ and $C$ is the boundary of the parallelogram with vertices $(0,0,1), \, (0,1,0), \, (2,0,-1)$, and $(2,1,-2)$.

Solution

To calculate the line integral directly, we need to parameterize each side of the parallelogram separately, calculate four separate line integrals, and add the result. This is not overly complicated, but it is time-consuming.

By contrast, let’s calculate the line integral using Stokes’ theorem. Let $S$ denote the surface of the parallelogram. Note that $S$ is the portion of the graph of $z = 1 - x - y$ for $(x,y)$ varying over the rectangular region with vertices $(0,0), \, (0,1), \, (2,0)$, and $(2,1)$ in the $xy$-plane. Therefore, a parameterization of $S$ is $\langle x,y, \, 1 - x - y \rangle, \, 0 \leq x \leq 2, \, 0 \leq y \leq 1$. The curl of $\vecs{F}$ is $\langle -z, \, 0, \, x \rangle$,and Stokes’ theorem and the equation for scalar surface integrals

$$\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &= \iint_S curl \, \vecs{F} \cdot d\vecs{S} \\[4pt] &= \int_0^2 \int_0^1 curl \, \vecs{F} (x,y) \cdot (\vecs t_x \times \vecs t_y) \, dy\, dx \\[4pt] &= \int_0^2 \int_0^1 \langle - (1 - x - y), \, 0, \, x \rangle \cdot ( \langle 1, \, 0, -1 \rangle \times \langle 0, \, 1, \, -1 \rangle ) \, dy \,dx \\[4pt] &= \int_0^2 \int_0^1 \langle x + y - 1, \, 0, \, x \rangle \cdot \langle 1, 1, 1 \rangle \, dy \, dx \\[4pt] &= \int_0^2 \int_0^1 2x + y - 1 \, dy \, dx \\[4pt] &= 3.\end{align*} \nonumber$$

Exercise $\PageIndex{3}$

Use Stokes’ theorem to calculate line integral

$$\int_C \vecs{F} \cdot d\vecs{r}, \nonumber$$

where $\vecs{F} = \langle z,x,y \rangle$ and $C$ is the boundary of a triangle with vertices $(0,0,1), \, (3,0,-2)$, and $(0,1,2)$.

Hint

This triangle lies in plane $z = 1 - x + y$.

Answer

$\dfrac{3}{2}$

Interpretation of Curl

In addition to translating between line integrals and flux integrals, Stokes’ theorem can be used to justify the physical interpretation of curl that we have learned. Here we investigate the relationship between curl and circulation, and we use Stokes’ theorem to state Faraday’s law—an important law in electricity and magnetism that relates the curl of an electric field to the rate of change of a magnetic field.

Recall that if $C$ is a closed curve and $\vecs{F}$ is a vector field defined on $C$, then the circulation of $\vecs{F}$ around $C$ is line integral

$$\int_C \vecs{F} \cdot d\vecs{r}. \nonumber$$

If $\vecs{F}$ represents the velocity field of a fluid in space, then the circulation measures the tendency of the fluid to move in the direction of $C$.

Let $\vecs{F}$ be a continuous vector field and let $D_{\tau}$ be a small disk of radius $r$ with center $P_0$ (Figure $\PageIndex{7}$). If $D_{\tau}$ is small enough, then $(curl \, \vecs{F})(P) \approx (curl \, \vecs F)(P_0)$ for all points $P$ in $D_{\tau}$ because the curl is continuous. Let $C_{\tau}$ be the boundary circle of $D_{\tau}$: By Stokes’ theorem,

$$\int_{C_{\tau}} \vecs{F} \cdot d\vecs{r} = \iint_{D_{\tau}} curl \, \vecs{F} \cdot \vecs{N} \, d\vecs S \approx \iint_{D_{\tau}} (curl \, \vecs{F})(P_0) \cdot \vecs{N} (P_0) \, d\vecs S. \nonumber$$

Figure $\PageIndex{7}$: Disk $D_{\tau}$ is a small disk in a continuous vector field.

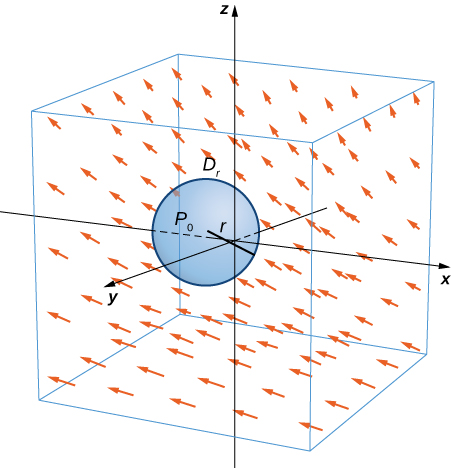
The quantity $(curl \, \vecs F)(P_0) \cdot \vecs N (P_0)$ is constant, and therefore

$$\iint_{D_{\tau}} (curl \, \vecs F)(P_0) \cdot \vecs N (P_0) \, d\vecs S = \pi r^2 [(curl \, \vecs F)(P_0) \cdot \vecs N (P_0)]. \nonumber$$

Thus

$$\int_{C_{\tau}} \vecs F \cdot d\vecs r \approx \pi r^2 [ (curl \, \vecs F)(P_0) \cdot \vecs N (P_0)], \nonumber$$

and the approximation gets arbitrarily close as the radius shrinks to zero. Therefore Stokes’ theorem implies that

$$(curl \, \vecs F)(P_0) \cdot \vecs N (P_0) = \lim_{r\rightarrow 0^+} \dfrac{1}{\pi r^2} \int_{C_{\tau}} \vecs F \cdot d\vecs r. \nonumber$$

This equation relates the curl of a vector field to the circulation. Since the area of the disk is $\pi r^2$, this equation says we can view the curl (in the limit) as the circulation per unit area. Recall that if $\vecs F$ is the velocity field of a fluid, then circulation $$\oint_{C_{\tau}} \vecs F \cdot d\vecs r = \oint_{C_{\tau}} \vecs F \cdot \vecs T \, ds \nonumber$$ is a measure of the tendency of the fluid to move around $C_{\tau}$: The reason for this is that $\vecs F \cdot \vecs T$ is a component of $\vecs F$ in the direction of $\vecs T$, and the closer the direction of $\vecs F$ is to $\vecs T$, the larger the value of $\vecs F \cdot \vecs T$ (remember that if $\vecs a$ and $\vecs b$ are vectors and $\vecs b$ is fixed, then the dot product $\vecs a \cdot \vecs b$ is maximal when $\vecs a$ points in the same direction as $\vecs b$). Therefore, if $\vecs F$ is the velocity field of a fluid, then $curl \, \vecs F \cdot \vecs N$ is a measure of how the fluid rotates about axis $\vecs N$. The effect of the curl is largest about the axis that points in the direction of $\vecs N$, because in this case $curl \, \vecs F \cdot \vecs N$ is as large as possible.

To see this effect in a more concrete fashion, imagine placing a tiny paddlewheel at point $P_0$ (Figure $\PageIndex{8}$). The paddlewheel achieves its maximum speed when the axis of the wheel points in the direction of curl $\vecs F$. This justifies the interpretation of the curl we have learned: curl is a measure of the rotation in the vector field about the axis that points in the direction of the normal vector $\vecs N$, and Stokes’ theorem justifies this interpretation.

Figure $\PageIndex{8}$: To visualize curl at a point, imagine placing a tiny paddlewheel at that point in the vector field.

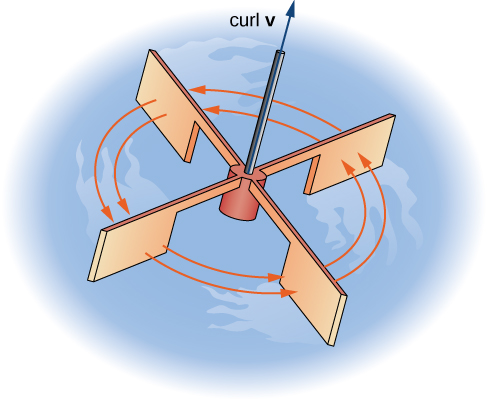
Now that we have learned about Stokes’ theorem, we can discuss applications in the area of electromagnetism. In particular, we examine how we can use Stokes’ theorem to translate between two equivalent forms of Faraday’s law. Before stating the two forms of Faraday’s law, we need some background terminology.

Let $C$ be a closed curve that models a thin wire. In the context of electric fields, the wire may be moving over time, so we write $C(t)$ to represent the wire. At a given time $t$, curve $C(t)$ may be different from original curve $C$ because of the movement of the wire, but we assume that $C(t)$ is a closed curve for all times $t$. Let $D(t)$ be a surface with $C(t)$ as its boundary, and orient $C(t)$ so that $D(t)$ has positive orientation. Suppose that $C(t)$is in a magnetic field $\vecs B(t)$ that can also change over time. In other words, $\vecs{B}$ has the form

$$\vecs B(x,y,z) = \langle P(x,y,z), \, Q(x,y,z), \, R(x,y,z) \rangle, \nonumber$$

where $P$, $Q$, and $R$ can all vary continuously over time. We can produce current along the wire by changing field $\vecs B(t)$ (this is a consequence of Ampere’s law). Flux $\displaystyle \phi (t) = \iint_{D(t)} \vecs B(t) \cdot d\vecs S$ creates electric field $\vecs E(t)$ that does work. The integral form of Faraday’s law states that

$$Work = \int_{C(t)} \vecs E(t) \cdot d\vecs r = - \dfrac{\partial \phi}{\partial t}. \nonumber$$

In other words, the work done by $\vecs{E}$ is the line integral around the boundary, which is also equal to the rate of change of the flux with respect to time. The differential form of Faraday’s law states that

$$curl \, \vecs{E} = - \dfrac{\partial \vecs B}{\partial t}. \nonumber$$

Using Stokes’ theorem, we can show that the differential form of Faraday’s law is a consequence of the integral form. By Stokes’ theorem, we can convert the line integral in the integral form into surface integral

$$-\dfrac{\partial \phi}{\partial t} = \int_{C(t)} \vecs E(t) \cdot d\vecs r = \iint_{D(t)} curl \,\vecs E(t) \cdot d\vecs S. \nonumber$$

Since $$\phi (t) = \iint_{D(t)} B(t) \cdot d\vecs S, \nonumber$$ then as long as the integration of the surface does not vary with time we also have

$$- \dfrac{\partial \phi}{\partial t} = \iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S. \nonumber$$

Therefore,

$$\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \,\vecs E \cdot d\vecs S. \nonumber$$

To derive the differential form of Faraday’s law, we would like to conclude that $curl \,\vecs E = -\dfrac{\partial \vecs B}{\partial t}$: In general, the equation

$$\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \,\vecs E \cdot d\vecs S \nonumber$$

is not enough to conclude that $curl \, \vecs E = -\dfrac{\partial \vecs B}{\partial t}$: The integral symbols do not simply “cancel out,” leaving equality of the integrands. To see why the integral symbol does not just cancel out in general, consider the two single-variable integrals $\displaystyle \int_0^1 x \, dx$ and $\displaystyle \int_0^1 f(x)\, dx$, where

$$f(x) = \begin{cases}1, &\text{if } 0 \leq x \leq 1/2 \\ 0, & \text{if } 1/2 \leq x \leq 1. \end{cases} \nonumber$$

Both of these integrals equal $\dfrac{1}{2}$, so $\displaystyle \int_0^1 x \, dx = \int_0^1 f(x) \, dx$.

However, $x \neq f(x)$. Analogously, with our equation $$\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \, \vecs E \cdot d\vecs S, \nonumber$$ we cannot simply conclude that $curl \, \vecs E = -\dfrac{\partial \vecs B}{\partial t}$ just because their integrals are equal. However, in our context, equation

$$\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \, \vecs E \cdot d\vecs S \nonumber$$

is true for any region, however small (this is in contrast to the single-variable integrals just discussed). If $\vecs F$ and $\vecs G$ are three-dimensional vector fields such that

$$\iint_S \vecs F \cdot d\vecs S = \iint_S \vecs G \cdot d\vecs S \nonumber$$

for any surface $S$, then it is possible to show that $\vecs F = \vecs G$ by shrinking the area of $S$ to zero by taking a limit (the smaller the area of $S$, the closer the value of $\displaystyle \iint_S \vecs F \cdot d\vecs S$ to the value of $\vecs F$ at a point inside $S$). Therefore, we can let area $D(t)$ shrink to zero by taking a limit and obtain the differential form of Faraday’s law:

$$curl \,\vecs E = - \dfrac{\partial \vecs B}{\partial t}. \nonumber$$

In the context of electric fields, the curl of the electric field can be interpreted as the negative of the rate of change of the corresponding magnetic field with respect to time.

Example $\PageIndex{4}$: Using Faraday’s Law

Calculate the curl of electric field $\vecs{E}$ if the corresponding magnetic field is constant field $\vecs B(t) = \langle 1, -4, 2 \rangle$.

Solution

Since the magnetic field does not change with respect to time, $-\dfrac{\partial \vecs B}{\partial t} = \vecs 0$. By Faraday’s law, the curl of the electric field is therefore also zero.

Analysis

A consequence of Faraday’s law is that the curl of the electric field corresponding to a constant magnetic field is always zero.

Exercise $\PageIndex{4}$

Calculate the curl of electric field $\vecs{E}$ if the corresponding magnetic field is $\vecs B(t) = \langle tx, \, ty, \, -2tz \rangle, \, 0 \leq t < \infty.$

Hint

• Use the differential form of Faraday’s law.
• Notice that the curl of the electric field does not change over time, although the magnetic field does change over time.

Answer

$curl \, \vecs{E} = \langle x, \, y, \, -2z \rangle$

Key Concepts

• Stokes’ theorem relates a flux integral over a surface to a line integral around the boundary of the surface. Stokes’ theorem is a higher dimensional version of Green’s theorem, and therefore is another version of the Fundamental Theorem of Calculus in higher dimensions.
• Stokes’ theorem can be used to transform a difficult surface integral into an easier line integral, or a difficult line integral into an easier surface integral.
• Through Stokes’ theorem, line integrals can be evaluated using the simplest surface with boundary $C$.
• Faraday’s law relates the curl of an electric field to the rate of change of the corresponding magnetic field. Stokes’ theorem can be used to derive Faraday’s law.

Key Equations

• Stokes’ theorem

$$\int_C \vecs{F} \cdot d\vecs{r} = \iint_S curl \, \vecs{F} \cdot d\vecs{S} \nonumber$$

Glossary

Stokes’ theorem

relates the flux integral over a surface $S$ to a line integral around the boundary $C$ of the surface $S$

surface independent

flux integrals of curl vector fields are surface independent if their evaluation does not depend on the surface but only on the boundary of the surface