16.3: Консервативні векторні поля

Цілі навчання

• Опишіть прості та замкнуті криві; визначте зв'язані та просто з'єднані області.
• Поясніть, як знайти потенційну функцію для консервативного векторного поля.
• Використовуйте фундаментальну теорему для лінійних інтегралів для оцінки лінійного інтеграла у векторному полі.
• Поясніть, як перевірити векторне поле, щоб визначити, чи є воно консервативним.

У цьому розділі ми продовжуємо вивчення консервативних векторних полів. Досліджується фундаментальна теорема для лінійних інтегралів, яка є корисним узагальненням фундаментальної теореми числення до лінійних інтегралів консервативних векторних полів. Ми також виявляємо, як перевірити, чи є дане векторне поле консервативним, і визначити, як побудувати потенційну функцію для векторного поля, відомого як консервативне.

Криві та регіони

Перш ніж продовжити дослідження консервативних векторних полів, потрібні деякі геометричні визначення. Теореми в наступних розділах покладаються на інтеграцію над певними видами кривих і регіонів, тому ми розробляємо визначення цих кривих і регіонів тут. Спочатку ми визначаємо два спеціальні види кривих: замкнуті криві та прості криві. Як ми дізналися, замкнута крива - це та, яка починається і закінчується в одній точці. Проста крива - це та, яка не перетинається сама. Крива, яка є одночасно замкнутою і простою, - це проста замкнута крива (рис.\(\PageIndex{1}\)).

Малюнок\(\PageIndex{1}\). Типи кривих, які є простими або не простими і замкнутими або не закритими.

ВИЗНАЧЕННЯ: Закриті криві

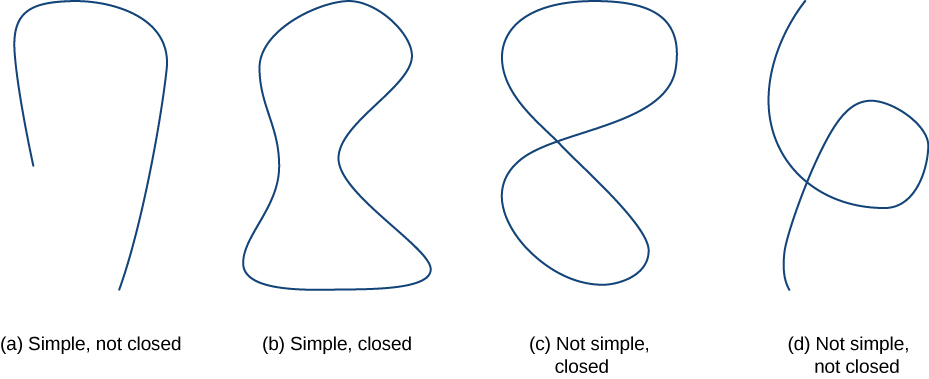
Крива\(C\) - це замкнута крива, якщо є\(a≤t≤b\) параметризація\(\vecs r(t)\),\(C\) такої, що параметризація проходить криву рівно один раз і\(\vecs r(a)=\vecs r(b)\). Крива\(C\) - це проста крива, якщо\(C\) не перетинається сама. \(C\)Тобто просто, якщо існує параметризація\(\vecs r(t)\),\(C\) таких,\(a≤t≤b\) що\(\vecs r\) один до одного закінчився\((a,b)\). Це можливо для\(\vecs r(a)=\vecs r(b)\), означає, що проста крива також замкнута.

Приклад\(\PageIndex{1}\): Determining Whether a Curve Is Simple and Closed

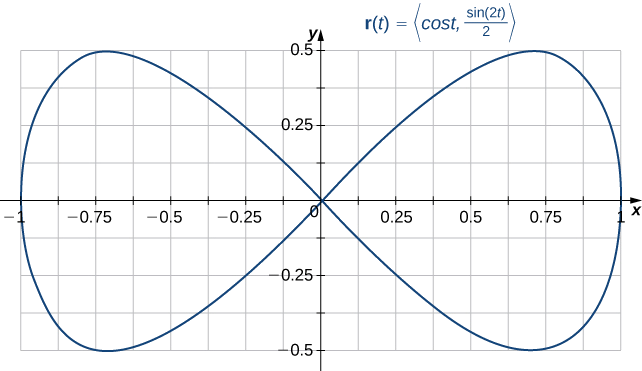
Крива з параметризацією\(\vecs{r}(t)=\left\langle\cos t,\frac{\sin(2t)}{2}\right\rangle\),\(0≤t≤2\pi\) проста замкнута крива?

Рішення

Зверніть увагу, що\(\vecs{r}(0)=⟨1,0⟩=\vecs r(2\pi)\); отже, крива замкнута. Однак крива не проста. Щоб переконатися в цьому, зверніть увагу на те\(\vecs{r}\left(\frac{\pi}{2}\right)=⟨0,0⟩=\vecs{r}\left(\frac{3\pi}{2}\right)\), що, і тому крива перетинає себе біля початку (рис.\(\PageIndex{2}\)).

Малюнок\(\PageIndex{2}\) . Крива, яка замкнута, але не проста.

Вправа\(\PageIndex{1}\)

Чи крива, задана параметризацією\(\vecs{r}(t)=⟨2\cos t,3\sin t⟩\)\(0≤t≤6\pi\), проста замкнута крива?

Підказка

Намалюйте криву.

Відповідь

Так

Багато теорем у цій главі пов'язують інтеграл над областю до інтегралу над межею області, де межа області є простою замкнутою кривою або об'єднанням простих замкнутих кривих. Щоб розробити ці теореми, нам потрібні два геометричні визначення регіонів: пов'язаної області та просто пов'язаної області. З'єднаний регіон - це той, в якому є шлях у регіоні, який з'єднує будь-які дві точки, що знаходяться в межах цього регіону. Просто з'єднана область - це зв'язана область, яка не має в ній отворів. Ці два поняття, поряд з поняттям простої замкнутої кривої, дозволяють викласти кілька узагальнень фундаментальної теореми числення пізніше в розділі. Ці два визначення дійсні для регіонів у будь-якій кількості вимірів, але ми стосуємося лише регіонів у двох-трьох вимірах.

ВИЗНАЧЕННЯ: підключені регіони

Область D є з'єднаною областю, якщо для будь-яких двох точок\(P_1\) і є шлях від\(P_1\) до\(P_2\) з слідом\(P_2\), що міститься повністю всередині D. Область D - це просто зв'язана область, якщо D з'єднана для будь-якої простої замкнутої кривої C, яка лежить всередині D, а крива C може безперервно скорочуватися до точки, залишаючись повністю всередині D. У двох вимірах область просто з'єднується, якщо вона підключена і не має отворів.

Всі просто підключені регіони з'єднані, але не всі підключені регіони просто з'єднуються (рис.\(\PageIndex{3}\)).

Малюнок\(\PageIndex{3}\): Не всі підключені регіони просто з'єднані. (a) Просто з'єднані області не мають отворів. (b) З'єднані області, які не просто з'єднані, можуть мати отвори, але ви все ще можете знайти шлях у регіоні між будь-якими двома точками. (c) Регіон, який не пов'язаний, має деякі точки, які не можуть бути з'єднані шляхом у регіоні.

Вправа\(\PageIndex{2}\)

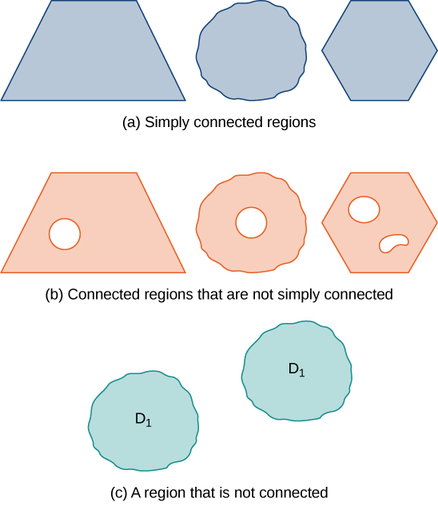
Чи пов'язаний регіон на зображенні нижче? Регіон просто пов'язаний?

Підказка

Розглянемо визначення.

Відповідь

Регіон на малюнку пов'язаний. Регіон на малюнку не просто пов'язаний.

Фундаментальна теорема для лінійних інтегралів

Тепер, коли ми розуміємо деякі основні криві та області, давайте узагальнимо фундаментальну теорему числення до лінійних інтегралів. Нагадаємо, що фундаментальна теорема обчислення говорить, що якщо функція\(f\) має антипохідну\(F\), то інтеграл\(f\) від\(a\) до\(b\) залежить тільки від значень\(F\) at\(a\) і at\(b\) —тобто,

\[\int_a^bf(x)\,dx=F(b)−F(a). \nonumber \]

Якщо розглядати градієнт як похідну, то така ж теорема тримає і для векторних лінійних інтегралів. Ми показуємо, як це працює на мотиваційному прикладі.

Приклад\(\PageIndex{2}\): Evaluating a Line Integral and the Antiderivatives of the Endpoints

Нехай\(\vecs{F}(x,y)=⟨2x,4y⟩\). Обчисліть\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), де C - відрізок лінії від\((0,0)\) до\((2,2)\) (рис.\(\PageIndex{4}\)).

Рішення

Використовуємо для розрахунку метод з попереднього розділу\(\int_C \vecs{F} \cdot d\vecs{r}\). Крива С може бути параметризована\(\vecs{r}(t)=⟨2t,2t⟩\),\(0≤t≤1\). Потім,\(\vecs{F}(\vecs r(t))=⟨4t,8t⟩\) і\(\vecs r′(t)=⟨2,2⟩\), з чого випливає, що

\[\begin{align*} \int_C \vecs{F}·d\vecs{r} &=\int_0^1⟨4t,8t⟩·⟨2,2⟩dt \\[4pt] &=\int_0^1(8t+16t)dt=\int_0^1 24tdt\\[4pt] &={\big[12t^2\big]}_0^1=12. \end{align*}\]

Малюнок\(\PageIndex{4}\): Значення лінійного інтеграла\(\int_C \vecs{F} \cdot d\vecs{r}\) залежить тільки від значення потенційної функції\(\vecs{F}\) в кінцевих точках кривої.

Зверніть увагу\(\vecs{F}=\vecs \nabla f\), що, де\(f(x,y)=x^2+2y^2\). Якщо розглядати градієнт як похідну, то\(f\) є «антидеривативом» від\(\vecs{F}\). У випадку однозмінних інтегралів інтеграл похідної\(g′(x)\) дорівнює\(g(b)−g(a)\), де a - початкова точка інтервалу інтегрування, а b - кінцева точка. Якщо векторні лінійні інтеграли працюють як однозмінні інтеграли, то ми очікуємо\(f(P_1)−f(P_0)\),\(P_1\) що інтеграл\(\vecs{F}\) буде, де кінцева точка кривої інтеграції і\(P_0\) є початковою точкою. Зверніть увагу, що це так для цього прикладу:

\[\int_C \vecs{F} \cdot d\vecs{r}=\int_C \vecs \nabla f \cdot d\vecs{r}=12 \nonumber \]

і

\[f(2,2)−f(0,0)=4+8−0=12. \nonumber \]

Іншими словами, інтеграл «похідної» можна обчислити, оцінюючи «антидериватив» в кінцевих точках кривої і віднімаючи, так само, як і для однозмінних інтегралів.

Наступна теорема говорить, що за певних умов те, що сталося в попередньому прикладі, стосується будь-якого градієнтного поля. Ця ж теорема тримає і для векторних лінійних інтегралів, які ми називаємо фундаментальною теоремою для лінійних інтегралів.

Теорема: ФУНДАМЕНТАЛЬНА ТЕОРЕМА ДЛЯ ЛІНІЙНИХ ІНТЕГРАЛІВ

Нехай С - кусково-плавна крива з параметризацією\(\vecs r(t)\),\(a≤t≤b\). \(f\)Дозволяти бути функцією двох або трьох змінних з частковими похідними першого порядку, які існують і є неперервними на C. Потім,

\[\int_C \vecs \nabla f \cdot d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \label{FunTheLine} \]

Доказ

По-перше,

\[\int_C \vecs \nabla f \cdot d \vecs{r}=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)\,dt. \nonumber \]

За правилом ланцюга,

\[\dfrac{d}{dt}(f( \vecs r(t))= \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t) \nonumber \]

Тому, за фундаментальною теоремою обчислення,

\[\begin{align*} \int_C \vecs \nabla f \cdot d \vecs{r} &=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)dt \\[4pt] &=\int_a^b\dfrac{d}{dt}(f( \vecs r(t))dt \\[4pt] &={\big[f( \vecs r(t))\big]}_{t=a}^{t=b}\\[4pt] &=f( \vecs r(b))−f( \vecs r(a)). \end{align*}\]

\(\square\)

Ми знаємо, що якщо\(\vecs{F}\) це консервативне векторне поле, є потенційна функція\(f\) така, що\( \vecs \nabla f= \vecs F\). Тому

\[\int_C \vecs F·d\vecs r=\int_C\vecs \nabla f·d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \nonumber \]

Іншими словами, так само, як і у випадку з фундаментальною теоремою обчислення, обчислення лінійного інтеграла\(\int_C \vecs F·d\vecs{r}\), де\(\vecs{F}\) консервативний, є двоетапним процесом:

1. Знайти потенційну функцію («антидериватив»)\(f\) для\(\vecs{F}\) і
2. Обчислити значення в кінцевих\(f\) точках\(C\) і обчислити їх різницю\(f(\vecs r(b))−f(\vecs r(a))\).

Майте на увазі, однак, існує одна головна відмінність між фундаментальною теоремою числення та фундаментальною теоремою для лінійних інтегралів:
функція однієї змінної, яка є безперервною, повинна мати антипохідну. Однак векторне поле, навіть якщо воно є безперервним, не повинно мати потенційну функцію.

Приклад\(\PageIndex{3}\): Applying the Fundamental Theorem

Обчислити інтеграл\(\int_C \vecs{F} \cdot d\vecs{r}\),\(C\) де\(\vecs{F}(x,y,z)=⟨2x\ln y,\dfrac{x^2}{y}+z^2,2yz⟩\) і - крива з параметризацією\(\vecs{r}(t)=⟨t^2,t,t⟩\),\(1≤t≤e\)

1. без використання фундаментальної теореми лінійних інтегралів і
2. з використанням фундаментальної теореми лінійних інтегралів.

Рішення

1. Спочатку обчислимо інтеграл без фундаментальної теореми для лінійних інтегралів і замість цього використаємо метод, який ми дізналися в попередньому розділі:

\[\begin{align*} \int_C \vecs{F} \cdot dr &=\int_1^e\vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt\\[4pt] &=\int_1^e⟨2t^2\ln t,\dfrac{t^4}{t}+t^2,2t^2⟩ \cdot ⟨2t,1,1⟩\,dt\\[4pt] &=\int_1^e(4t^3\ln t+t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t \,dt+\int_1^e(t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t\,dt+{\Big[\dfrac{t^4}{4}+t^3\Big]}_1^e \\[4pt] &=\int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{1}{4} −1 \\[4pt] &= \int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{5}{4}\end{align*}\]

Інтегральна\(\displaystyle \int_1^e t^3\ln t\,dt\) вимагає інтеграції частинами. Нехай\(u=\ln t\) і\(dv=t^3\). Потім\(u=\ln t\),\(dv=t^3\)

і

\[du=\dfrac{1}{t}\,dt, \;\;v=\dfrac{t^4}{4}.\nonumber \]

Тому

\[\begin{align*} \int_1^e t^3\ln t\,dt &={\Big[\dfrac{t^4}{4}\ln t\Big]}_1^e−\dfrac{1}{4}\int_1^e t^3\,dt \\[4pt] &=\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right). \end{align*}\]

Таким чином,

\[\begin{align*} \int_C \vecs F \cdot d\vecs{r} &= 4\int_1^e t^3\ln t\, dt\quad +\quad \dfrac{e^4}{4}+e^3 − \dfrac{5}{4} \\[4pt] &=4\left(\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right)\right)+\dfrac{e^4}{4}+e^3−\dfrac{5}{4}\\[4pt] &=e^4−\dfrac{e^4}{4}+\dfrac{1}{4}+\dfrac{e^4}{4}+e^3−\dfrac{5}{4} \\[4pt] &=e^4+e^3−1. \end{align*}\]

2. Враховуючи, що\(f(x,y,z)=x^2\ln y+yz^2\) є потенційною функцією для\(\vecs F\), давайте використаємо фундаментальну теорему для лінійних інтегралів для обчислення інтеграла. Зауважте, що

\[\begin{align*} \int_C \vecs F \cdot d\vecs{r} &=\int_C \vecs \nabla f \cdot d\vecs{r} \\[4pt] &=f(\vecs r(e))−f(\vecs r(1)) \\[4pt] &=f(e^2,e,e)−f(1,1,1)\\[4pt] &=e^4+e^3−1. \end{align*}\]

Цей розрахунок набагато простіший, ніж розрахунок, який ми зробили в (а). Поки у нас є потенційна функція, обчислення лінійного інтеграла за допомогою Фундаментальної теореми для лінійних інтегралів набагато простіше, ніж обчислення без теореми.

Приклад\(\PageIndex{3}\) ілюструє приємну особливість фундаментальної теореми лінійних інтегралів: вона дозволяє нам легше обчислити багато векторних лінійних інтегралів. Поки у нас є потенційна функція, обчислення лінійного інтеграла - це лише питання оцінки потенційної функції в кінцевих точках та віднімання.

Вправа\(\PageIndex{3}\)

Враховуючи, що\(f(x,y)={(x−1)}^2y+{(y+1)}^2x\) є потенційною функцією для\(\vecs F(x,y)=⟨2xy−2y+{(y+1)}^2,{(x−1)}^2+2yx+2x⟩\), обчислити інтеграл\(\int_C \vecs F·d\vecs r\), де\(C\) нижня половина одиничного кола орієнтована проти годинникової стрілки.

Підказка

Фундаментальна теорема для лінійних інтервалів говорить, що цей інтеграл залежить тільки від значення\(f\) в кінцевих точках\(C\).

Відповідь

2

Фундаментальна теорема для лінійних інтегралів має два важливі наслідки. Перший наслідок полягає в тому, що якщо\(\vecs{F}\) консервативний і\(C\) є замкнутою кривою, то циркуляція\(\vecs{F}\) вздовж\(C\) дорівнює нулю - тобто\(\int_C \vecs F·d\vecs r=0\). Щоб зрозуміти, чому це правда, нехай\(f\) буде потенційна функція для\(\vecs{F}\). Оскільки\(C\) це замкнута крива,\(\vecs r(b)\) кінцева точка\(C\) є такою ж, як початкова\(\vecs r(a)\)\(C\) - тобто\(\vecs r(a)=\vecs r(b)\). Тому, за фундаментальною теоремою для лінійних інтегралів,

\[\begin{align} \oint_C \vecs F·d\vecs r &=\oint_C \vecs \nabla f·d\vecs r\\[4pt] &=f(\vecs r(b))−f(\vecs r(a)) \\[4pt] &=f(\vecs r(b))−f(\vecs r(b)) \\[4pt] &=0. \end{align} \nonumber \]

Нагадаємо, що причина консервативного векторного поля\(\vecs{F}\) називається «консервативним», полягає в тому, що такі векторні поля моделюють сили, в яких зберігається енергія. Ми показали, що гравітація є прикладом такої сили. Якщо розглядати векторне поле\(\vecs{F}\) в\(\oint_C \vecs F·d\vecs r\) інтегралі як гравітаційне поле, то рівняння\(\oint_C \vecs{F}·d\vecs{r}=0\) слід. Якщо частинка рухається по шляху, який починається і закінчується в одному і тому ж місці, то робота, виконана гравітацією над частинкою, дорівнює нулю.

Другим важливим наслідком фундаментальної теореми для лінійних інтегралів (Equation\ ref {FuntheLine}) є те, що лінійні інтеграли консервативних векторних полів не залежать від шляху, тобто вони залежать лише від кінцевих точок заданої кривої і не залежать від шляху між кінцевими точками.

ВИЗНАЧЕННЯ: Шляхи Незалежності

\(\vecs{F}\)Дозволяти векторне поле з доменом\(D\); він не залежить від шляху (або шляху незалежний), якщо

\[\int_{C_1} \vecs{F}·d\vecs{r}=\int_{C_2} \vecs{F}·d\vecs{r} \nonumber \]

для будь-яких шляхів\(C_1\) і\(C_2\) в\(D\) з однаковими початковими і кінцевими точками.

Друге наслідок викладено формально в наступній теоремі.

Теорема: КОНСЕРВАТИВНІ ПОЛЯ

Якщо\(\vecs{F}\) є консервативним векторним полем,\(\vecs{F}\) то не залежить від шляху.

Доказ

\(D\)Дозволяти позначити область\(\vecs{F}\) і нехай\(C_1\) і\(C_2\) бути два шляхи в\(D\) з однаковими початковими і кінцевими точками (рис.\(\PageIndex{5}\)). Викликати початкову точку\(P_1\) і кінцеву точку\(P_2\). \(\vecs{F}\)Оскільки консервативний, існує потенційна функція\(f\) для\(\vecs{F}\). За фундаментальною теоремою для лінійних інтегралів

\[\int_{C_1} \vecs{F}·d\vecs{r}=f(P_2)−f(P_1)=\int_{C_2} \vecs{F}·d\vecs{r}. \nonumber \]

Тому\(\int_{C_1}\vecs F·d\vecs r=\int_{C_2}\vecs F·d\vecs r\) і\(\vecs{F}\) є незалежним від шляху.

\(\square\)

Щоб уявити, що означає незалежність шляху, уявіть трьох туристів, що піднімаються з базового табору на вершину гори. Мандрівний 1 проходить крутий маршрут прямо з табору на вершину. Hiker 2 проходить звивистий маршрут, який не крутий від табору до вершини. Мандрівний 3 починається з крутого маршруту, але на півдорозі до вершини вирішує, що це занадто важко для нього. Тому він повертається в табір і йде некрутою стежкою на вершину. Всі троє туристів подорожують стежками в гравітаційному полі. Оскільки гравітація - це сила, в якій зберігається енергія, гравітаційне поле консервативне. За незалежністю шляху, загальний обсяг робіт, виконаних гравітацією на кожного з туристів, однаковий, тому що всі вони починалися в одному і тому ж місці і закінчувалися на одному місці. Робота, яку виконують туристи, включає інші фактори, такі як тертя та рух м'язів, тому загальна кількість енергії, яку кожен витрачає, не однакова, але чиста енергія, витрачена проти сили тяжіння, однакова для всіх трьох туристів.

Малюнок\(\PageIndex{4}\): Векторне поле консервативне, а отже, не залежить від шляху.

Ми показали, що якщо\(\vecs{F}\) консервативний,\(\vecs{F}\) то незалежний від шляху. Виходить, що якщо домен\(\vecs{F}\) відкритий і підключений, то зворотне теж вірно. Тобто, якщо\(\vecs{F}\) не залежить від шляху, а область відкрита і пов'язана,\(\vecs{F}\) то консервативна.\(\vecs{F}\) Тому множина консервативних векторних полів на відкритих і зв'язаних областях є саме сукупністю векторних полів, незалежних від шляху.

Теорема: ТЕСТ НА НЕЗАЛЕЖНІСТЬ ШЛЯХУ ДЛЯ КОНСЕРВАТИВНИХ ПОЛІВ

Якщо\(\vecs{F}\) це безперервне векторне поле, яке не залежить від шляху, а область\(D\)\(\vecs{F}\) відкритого і пов'язаного,\(\vecs{F}\) то консервативне.

Доказ

Доведено теорему для векторних полів в\(ℝ^2\). Доказ для векторних полів в\(ℝ^3\) аналогічний. Щоб показати,\(\vecs F=⟨P,Q⟩\) що консервативно, ми повинні знайти потенційну функцію\(f\) для\(\vecs{F}\). З цією метою, нехай\(X\) бути фіксованою точкою в\(D\). Для будь-якої точки\((x,y)\) в\(D\),\(C\) нехай шлях від\(X\) до\((x,y)\). Визначте\(f(x,y)\) по\(f(x,y)=\int_C \vecs F·d\vecs r\). (Зауважте, що це визначення має\(f\) сенс лише тому\(\vecs{F}\), що не залежить від шляху. \(\vecs{F}\)Якби не був незалежний від шляху, то можна було б знайти інший шлях\(C′\) від\(X\) до\((x,y)\) такого\(\int_C \vecs F·d\vecs r≠\int_C \vecs F·d\vecs r\), що, і в такому випадку не\(f(x,y)\) буде функцією.) Ми хочемо показати, що\(f\) має властивість\(\vecs \nabla f=\vecs F\).

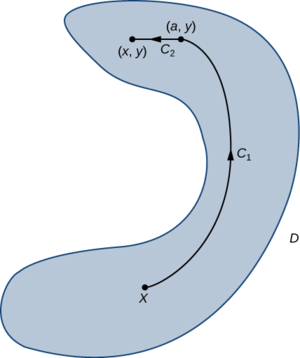
Оскільки домен\(D\) відкритий, можна знайти диск з центром\((x,y)\) таким чином, щоб диск містився повністю всередині\(D\). \(a<x\)Дозволяти\((a,y)\) з бути точкою в цьому диску. \(C\)Дозволяти шлях від\(X\) до\((x,y)\), що складається з двох частин:\(C_1\) і\(C_2\). Перший шматок - це будь-який шлях від\(C\) до\(C_1\),\((a,y)\) який залишається всередині\(D\);\(C_2\) це відрізок горизонтальної лінії від\((a,y)\) до\((x,y)\) (Рисунок\(\PageIndex{6}\)). Тоді

\[f(x,y)=\int_{C_1} \vecs F·d\vecs r+\int_{C_2}\vecs F \cdot d\vecs r.\nonumber \]

Перший інтеграл не залежить від\(x\), тому

\[f_x(x,y)=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r. \nonumber \]

Якщо ми параметризуємо\(C_2\) по\(\vecs r(t)=⟨t,y⟩\)\(a≤t≤x\), то

\[\begin{align*} f_x(x,y) &=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \dfrac{d}{dt}(⟨t,y⟩)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot ⟨1,0⟩\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt.\\[4pt] \end{align*}\]

За фундаментальною теоремою обчислення (частина 1)

\[f_x(x,y)=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt=P(x,y).\nonumber \]

Малюнок\(\PageIndex{6}\). Тут\(C_1\) є будь-який шлях від\(C\) до,\((a,y)\) який залишається всередині\(D\), і\(C_2\) горизонтальний відрізок лінії від\((a,y)\) до\((x,y)\).

Подібний аргумент, що використовує відрізок вертикальної лінії, а не горизонтальний відрізок лінії показує, що\(f_y(x,y)=Q(x,y)\).

Тому\(\vecs \nabla f=\vecs F\) і\(\vecs{F}\) є консервативним.

\(\square\)

Ми витратили багато часу на обговорення та доведення теорем вище, але ми можемо їх узагальнити просто: векторне поле\(\vecs F\) на відкритій та пов'язаній області консервативне тоді і лише тоді, коли воно не залежить від шляху. Це важливо знати, оскільки консервативні векторні поля надзвичайно важливі в додатках, і ці теореми дають нам інший спосіб перегляду того, що означає бути консервативним, використовуючи незалежність шляху.

Приклад\(\PageIndex{4}\): Showing That a Vector Field Is Not Conservative

Використовуйте незалежність шляху, щоб показати, що векторне поле не\(\vecs F(x,y)=⟨x^2y,y+5⟩\) є консервативним.

Рішення

Ми можемо вказати, що\(\vecs{F}\) це не консервативно, показавши, що\(\vecs{F}\) це не шлях незалежний. Ми робимо це, даючи два різні шляхи,\(C_1\) і\(C_2\), що обидва починаються\((0,0)\) і закінчуються\((1,1)\), і все ж\(\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r\).

\(C_1\)Дозволяти крива з параметризацією\(\vecs r_1(t)=⟨t,\,t⟩\),\(0≤t≤1\) і\(C_2\) нехай крива з параметризацією\(\vecs r_2(t)=⟨t,\,t^2⟩\),\(0≤t≤1\) (рис\(\PageIndex{7}\).). Тоді

\[\begin{align*} \int_{C_1} \vecs{F}·d\vecs r &=\int_0^1 \vecs F(\vecs r_1(t))·\vecs r_1′(t)\,dt \\[4pt] &=\int_0^1⟨t^3,t+5⟩·⟨1,1⟩\,dt=\int_0^1(t^3+t+5)\,dt\\[4pt] &={\Big[\dfrac{t^4}{4}+\dfrac{t^2}{2}+5t\Big]}_0^1=\dfrac{23}{4} \end{align*}\]

і

\[\begin{align*} \int_{C_2}\vecs F·d\vecs r &=\int_0^1 \vecs F(\vecs r_2(t))·\vecs r_2′(t)\,dt \\[4pt] &=\int_0^1⟨t^4,t^2+5⟩·⟨1,2t⟩\,dt=\int_0^1(t^4+2t^3+10t)\,dt \\[4pt] &={\Big[\dfrac{t^5}{5}+\dfrac{t^4}{2}+5t^2\Big]}_0^1=\dfrac{57}{10}. \end{align*}\]

Так як\(\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r\), значення прямої інтеграла\(\vecs{F}\) залежить від шляху між двома заданими точками. Тому не\(\vecs{F}\) є незалежним від шляху, і не\(\vecs{F}\) є консервативним.

Малюнок\(\PageIndex{7}\):\(C_2\) Криві\(C_1\) і обидва орієнтовані зліва направо.

Вправа\(\PageIndex{4}\)

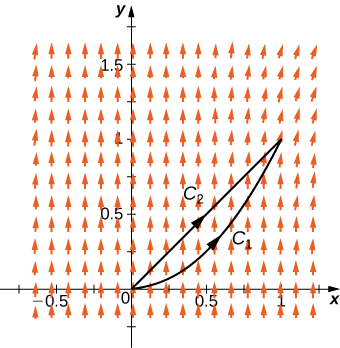
Показати, що не\(\vecs{F}(x,y)=⟨xy,\,x^2y^2⟩\) є незалежним від шляху, враховуючи відрізок лінії від\((0,0)\) до\((0,2)\) і фрагмент графіка\(y=\dfrac{x^2}{2}\), який йде від\((0,0)\) до\((0,2)\).

Підказка

Обчисліть відповідні лінійні інтеграли.

Відповідь

Якщо\(C_1\) і\(C_2\) представляють дві криві, то\[\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r. \nonumber \]

Консервативні векторні поля та потенційні функції

Як ми дізналися, фундаментальна теорема для лінійних інтегралів говорить,\(\vecs{F}\) що якщо консервативне, то обчислення\(\int_C \vecs F·d\vecs r\) має два кроки: по-перше, знайти потенційну функцію\(f\) для\(\vecs{F}\) і, по-друге\(f(P_1)−f(P_0)\), обчислити, де\(P_1\) кінцева точка\(C\) і\(P_0\) є відправною точкою. Щоб використовувати цю теорему для консервативного поля\(\vecs{F}\), ми повинні вміти знайти потенційну функцію\(f\) для\(\vecs{F}\). Тому ми повинні відповісти на наступне питання: З огляду на консервативне векторне поле\(\vecs{F}\), як знайти функцію\(f\) таку, що\(\vecs \nabla f=\vecs{F}\)? Перш ніж дати загальний метод знаходження потенційної функції, мотивуємо метод прикладом.

Приклад\(\PageIndex{5}\): Finding a Potential Function

Знайдіть потенційну функцію для\(\vecs F(x,y)=⟨2xy^3,3x^2y^2+\cos(y)⟩\), тим самим показуючи,\(\vecs{F}\) що консервативна.

Рішення

Припустимо, що\(f(x,y)\) це потенційна функція для\(\vecs{F}\). Потім\(\vecs \nabla f=\vecs F\), і тому

\[f_x(x,y)=2xy^3 \; \; \text{and} \;\; f_y(x,y)=3x^2y^2+\cos y. \nonumber \]

Інтеграція рівняння\(f_x(x,y)=2xy^3\) щодо\(x\) дає рівняння

\[f(x,y)=x^2y^3+h(y). \nonumber \]

Зверніть увагу, що оскільки ми інтегруємо функцію з двома змінними щодо\(x\), ми повинні додати константу інтеграції, яка є постійною щодо\(x\), але все ще може бути функцією\(y\). Рівняння\(f(x,y)=x^2y^3+h(y)\) можна підтвердити, взявши часткову похідну щодо\(x\):

\[\dfrac{∂f}{∂x}=\dfrac{∂}{∂x}(x^2y^3)+\dfrac{∂}{∂x}(h(y))=2xy^3+0=2xy^3. \nonumber \]

Оскільки\(f\) є потенційною функцією для\(\vecs{F}\),

\[f_y(x,y)=3x^2y^2+\cos(y), \nonumber \]

і тому

\[3x^2y^2+g′(y)=3x^2y^2+\cos(y). \nonumber \]

Це означає\(h′(y)=\cos y\), що, так\(h(y)=\sin y+C\). Тому будь-яка функція форми\(f(x,y)=x^2y^3+\sin(y)+C\) є потенційною функцією. Беручи, зокрема,\(C=0\) дає потенційну функцію\(f(x,y)=x^2y^3+\sin(y)\).

Щоб перевірити, що\(f\) це потенційна функція, зауважте, що\(\vecs \nabla f(x,y)=⟨2xy^3,3x^2y^2+\cos y⟩=\vecs F\).

Вправа\(\PageIndex{5}\)

Знайдіть потенційну функцію для\(\vecs{F}(x,y)=⟨e^xy^3+y,3e^xy^2+x⟩\).

Підказка

Дотримуйтесь інструкцій, описаних у прикладі\(\PageIndex{5}\).

Відповідь

\(f(x,y)=e^xy^3+xy\)

Логіка попереднього прикладу поширюється на знаходження потенційної функції для будь-якого консервативного векторного поля в\(ℝ^2\). Таким чином, ми маємо наступну стратегію вирішення проблем пошуку потенційних функцій:

СТРАТЕГІЯ ВИРІШЕННЯ ЗАДАЧ: ПОШУК ПОТЕНЦІЙНОЇ ФУНКЦІЇ КОНСЕРВАТИВНОГО ВЕКТОРНОГО ПОЛЯ\(\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩\)

1. \(P\)Інтегрувати по відношенню до\(x\). Це призводить до функції форми\(g(x,y)+h(y)\), де\(h(y)\) невідомо.
2. Візьміть часткову\(g(x,y)+h(y)\) похідну по відношенню до\(y\), яка призводить до функції\(gy(x,y)+h′(y)\).
3. Використовуйте рівняння\(gy(x,y)+h′(y)=Q(x,y)\), щоб знайти\(h′(y)\).
4. Інтегруйте\(h′(y)\), щоб знайти\(h(y)\).
5. Будь-яка функція форми\(f(x,y)=g(x,y)+h(y)+C\), де\(C\) константа, є потенційною функцією для\(\vecs{F}\).

Ми можемо адаптувати цю стратегію, щоб знайти потенційні функції для векторних полів у\(ℝ^3\), як показано в наступному прикладі.

Приклад\(\PageIndex{6}\): Finding a Potential Function in \(ℝ^3\)

Знайдіть потенційну функцію для\(F(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩\), тим самим показуючи,\(\vecs{F}\) що консервативна.

Рішення

Припустимо, що\(f\) це потенційна функція. Тоді,\(\vecs \nabla f= \vecs{F}\) і тому\(f_x(x,y,z)=2xy\). Інтеграція цього рівняння щодо\(x\) дає рівняння\(f(x,y,z)=x^2y+g(y,z)\) для деякої функції\(g\). Зверніть увагу, що в цьому випадку константа інтеграції щодо\(x\) є функцією\(y\) і\(z\).

Оскільки\(f\) є потенційною функцією,

\[x^2+2yz^3=f_y(x,y,z)=x^2+g_y(y,z). \nonumber \]

Тому

\[g_y(y,z)=2yz^3. \nonumber \]

Інтеграція цієї функції щодо\(y\) врожайності

\[g(y,z)=y^2z^3+h(z) \nonumber \]

для якоїсь функції\(h(z)\)\(z\) поодинці. (Зверніть увагу, що, тому що ми знаємо, що\(g\) це функція тільки\(y\) і\(z\), нам не потрібно писати\(g(y,z)=y^2z^3+h(x,z)\).) Тому

\[f(x,y,z)=x^2y+g(y,z)=x^2y+y^2z^3+h(z). \nonumber \]

Щоб знайти\(f\), нам тепер залишається тільки знайти\(h\). Оскільки\(f\) є потенційною функцією,

\[3y^2z^2+2z=g_z(y,z)=3y^2z^2+h′(z). \nonumber \]

Це означає\(h′(z)=2z\), що, так\(h(z)=z^2+C\). Дозволяючи\(C=0\) дає потенційну функцію

\[f(x,y,z)=x^2y+y^2z^3+z^2. \nonumber \]

Щоб перевірити, що\(f\) це потенційна функція, зауважте, що\(\vecs \nabla f(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩=\vecs F(x,y,z)\).

Вправа\(\PageIndex{6}\)

Знайдіть потенційну функцію для\(\vecs{F}(x,y,z)=⟨12x^2,\cos y\cos z,1−\sin y\sin z⟩\).

Підказка

Наступний приклад\(\PageIndex{6}\), почніть з інтеграції щодо\(x\).

Відповідь

\(f(x,y,z)=4x^3+\sin y\cos z+z\)

Ми можемо застосувати процес знаходження потенційної функції до гравітаційної сили. Нагадаємо, що, якщо об'єкт має одиничну масу і знаходиться біля початку, то гравітаційна сила в\(ℝ^2\) тому, що об'єкт чинить на інший об'єкт одиничної маси в точці,\((x,y)\) задається векторним полем

\(\vecs F(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle\),

де\(G\) - універсальна гравітаційна константа. У наступному прикладі ми будуємо потенційну функцію для\(\vecs{F}\), тим самим підтверджуючи те, що ми вже знаємо: що гравітація консервативна.

Приклад\(\PageIndex{7}\): Finding a Potential Function

Знайдіть потенційну функцію\(f\) для\(\vecs{F}(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle\).

Рішення

Припустимо, що\(f\) це потенційна функція. Тоді,\(\vecs \nabla f= \vecs{F}\) і тому

\[f_x(x,y)=\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }.\nonumber \]

Щоб інтегрувати цю функцію щодо\(x\), ми можемо використовувати\(u\) -підстановку. Якщо\(u=x^2+y^2\), то\(\dfrac{du}{2}=x\,dx\), так

\[\begin{align*} \int \dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }\,dx &=\int \dfrac{−G}{2u^{3/2}} \,du \\[4pt] &=\dfrac{G}{\sqrt{u}}+h(y) \\[4pt] &=\dfrac{G}{\sqrt{x^2+y^2}}+h(y) \end{align*}\]

для якоїсь функції\(h(y)\). Тому

\[f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y).\nonumber \]

Оскільки\(f\) є потенційною функцією для\(\vecs{F}\),

\[f_y(x,y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }\nonumber \].

Так як\(f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y)\),\(f_y(x,y)\) також дорівнює\(\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)\).

Тому

\[\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }, \nonumber \]

що означає, що\(h′(y)=0\). Таким чином, ми можемо\(h(y)\) прийняти будь константа; зокрема, ми можемо дозволити\(h(y)=0\). Функція

\[f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2} } \nonumber \]

є потенційною функцією для гравітаційного поля\(\vecs{F}\). Щоб підтвердити, що\(f\) це потенційна функція, зауважте, що

\[\begin{align*} \vecs\nabla f(x,y) &=⟨−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} } (2x),−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} }(2y)⟩ \\[4pt] &=⟨\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }⟩\\[4pt] &=\vecs F(x,y). \end{align*}\]

Вправа\(\PageIndex{7}\)

Знайдіть потенційну функцію\(f\) для тривимірної гравітаційної сили\(\vecs{F}(x,y,z)=\left\langle\dfrac{−Gx}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gz}{ {(x^2+y^2+z^2)}^{3/2} }\right\rangle\).

Підказка

Дотримуйтесь стратегії вирішення проблем.

Відповідь

\(f(x,y,z)=\dfrac{G}{\sqrt{x^2+y^2+z^2}}\)

Тестування векторного поля

До цих пір ми працювали з векторними полями, які, як ми знаємо, є консервативними, але якщо нам не кажуть, що векторне поле консервативне, нам потрібно мати можливість перевірити, чи є воно консервативним. Нагадаємо, що якщо\(\vecs{F}\) консервативний, то\(\vecs{F}\) має перехресну часткову властивість (див. Перехресне часткове властивість консервативних векторних полів). Тобто якщо\(\vecs F=⟨P,Q,R⟩\) консервативний, то\(P_y=Q_x\)\(P_z=R_x\), і\(Q_z=R_y\). Отже, якщо\(\vecs{F}\) має перехресне часткове властивість, то\(\vecs{F}\) консервативна? Якщо домен\(\vecs{F}\) відкритий і просто підключений, то відповідь - так.

Теорема: КРОС-ЧАСТКОВИЙ ТЕСТ ДЛЯ КОНСЕРВАТИВНИХ ПОЛІВ

Якщо\(\vecs{F}=⟨P,Q,R⟩\) є векторним полем на відкритій, просто пов'язаної області\(D\) і\(P_y=Q_x\)\(P_z=R_x\), і\(Q_z=R_y\) по всьому\(D\),\(\vecs{F}\) то консервативне.

Хоча доказ цієї теореми виходить за рамки тексту, ми можемо виявити її силу на деяких прикладах. Пізніше ми бачимо, чому необхідно, щоб регіон був просто підключений.

Об'єднавши цю теорему з перехресним частинним властивістю, можна визначити, чи є задане векторне поле консервативним:

Теорема: КРОС-ЧАСТКОВА ВЛАСТИВІСТЬ КОНСЕРВАТИВНИХ ПОЛІВ

\(\vecs{F}=⟨P,Q,R⟩\)Дозволяти векторне поле на відкритій, просто пов'язаної області\(D\). Потім\(P_y=Q_x\)\(P_z=R_x\), і\(Q_z=R_y\) протягом того,\(D\) якщо і тільки\(\vecs{F}\) консервативний.

Версія цієї теореми в також\(ℝ^2\) вірна. Якщо\(\vecs F(x,y)=⟨P,Q⟩\) є векторним полем на відкритому, просто підключеному домені в\(ℝ^2\),\(\vecs F\) то консервативне, якщо і тільки якщо\(P_y=Q_x\).

Приклад\(\PageIndex{8}\): Determining Whether a Vector Field Is Conservative

Визначте, чи\(\vecs F(x,y,z)=⟨xy^2z,x^2yz,z^2⟩\) є векторне поле консервативним.

Рішення

Зверніть увагу, що домен\(\vecs{F}\) є все\(ℝ^2\) і\(ℝ^3\) просто підключений. Тому ми можемо використовувати перехресну часткову властивість консервативних векторних полів, щоб визначити, чи\(\vecs{F}\) є консервативним. Нехай

\[P(x,y,z)=xy^2z \nonumber \]

\[Q(x,y,z)=x^2yz \nonumber \]

і

\[R(x,y,z)=z^2.\nonumber \]

Оскільки\(Q_z(x,y,z)=x^2y\) і\(R_y(x,y,z)=0\), векторне поле не консервативне.

Приклад\(\PageIndex{9}\): Determining Whether a Vector Field Is Conservative

Визначити\(\vecs{F}(x,y)=⟨x\ln (y), \,\dfrac{x^2}{2y}⟩\) векторне поле консервативно.

Рішення

Зверніть увагу, що домен\(\vecs{F}\) - це частина,\(ℝ^2\) в якій\(y>0\). Таким чином, домен\(\vecs{F}\) є частиною площини над\(x\) -віссю, і цей домен просто пов'язаний (в цій області немає дірок і ця область пов'язана). Тому ми можемо використовувати перехресну часткову властивість консервативних векторних полів, щоб визначити, чи\(\vecs{F}\) є консервативним. Нехай

\[P(x,y)=x\ln (y) \;\; \text{and} \;\;\ Q(x,y)=\dfrac{x^2}{2y}. \nonumber \]

Тоді\(P_y(x,y)=\dfrac{x}{y}=Q_x(x,y)\) і таким чином\(\vecs{F}\) є консервативним.

Вправа\(\PageIndex{8}\)

Визначте, чи\(\vecs{F}(x,y)=⟨\sin x\cos y,\,\cos x\sin y⟩\) є консервативним.

Підказка

Використовуйте перехресну часткову властивість консервативних векторних полів з попереднього розділу.

Відповідь

Він консервативний.

При використанні перехресної часткової властивості консервативних векторних полів важливо пам'ятати, що теорема є інструментом, і, як і будь-який інструмент, вона може бути застосована тільки за правильних умов. У випадку перехресної часткової властивості консервативних векторних полів теорема може бути застосована тільки в тому випадку, якщо область векторного поля просто пов'язана.

Щоб побачити, що може піти не так при неправильному застосуванні теореми, розглянемо векторне поле з Прикладу\(\PageIndex{4}\):

\[\vecs F(x,y)=\dfrac{y}{x^2+y^2}\,\hat{\mathbf i}+\dfrac{−x}{x^2+y^2}\,\hat{\mathbf j}. \nonumber \]

Це векторне поле задовольняє перехресно-часткову властивість, так як

\[\dfrac{∂}{∂y}\left(\dfrac{y}{x^2+y^2}\right)=\dfrac{(x^2+y^2)−y(2y)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2} \nonumber \]

і

\[\dfrac{∂}{∂x}\left(\dfrac{−x}{x^2+y^2}\right)=\dfrac{−(x^2+y^2)+x(2x)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2}. \nonumber \]

Оскільки\(\vecs{F}\) задовольняє перехресну часткову властивість, ми можемо спокуситися зробити висновок, що\(\vecs{F}\) це консервативне. Однак не\(\vecs{F}\) є консервативним. Щоб переконатися в цьому, нехай

\[\vecs r(t)=⟨\cos t,\sin t⟩,\;\; 0≤t≤\pi \nonumber \]

бути параметризації верхньої половини одиниці окружності, орієнтованої проти годинникової стрілки (позначають це\(C_1\)) і нехай

\[\vecs s(t)=⟨\cos t,−\sin t⟩,\;\; 0≤t≤\pi \nonumber \]

бути параметризацією нижньої половини одиничного кола, орієнтованого за годинниковою стрілкою (позначають це\(C_2\)). Зверніть увагу, що\(C_1\) і\(C_2\) мають однакову початкову точку і кінцеву точку. З тих пір\({\sin}^2 t+{\cos}^2 t=1\),

\[\vecs F(\vecs r(t)) \cdot \vecs r′(t)=⟨\sin(t),−\cos(t)⟩ \cdot ⟨−\sin(t), \cos(t)⟩=−1 \nonumber \]

і

\[\vecs F(\vecs s(t))·\vecs s′(t)=⟨−\sin t,−\cos t⟩·⟨−\sin t,−\cos t⟩={\sin}^2 t+{\cos}^2t=1. \nonumber \]

Тому

\[\int_{C_1} \vecs F·d\vecs r=\int_0^{\pi}−1\,dt=−\pi \nonumber \]

і

\[\int_{C_2}\vecs F·d\vecs r=\int_0^{\pi} 1\,dt=\pi. \nonumber \]

Таким чином,\(C_1\) і\(C_2\) мають однакову початкову точку і кінцеву точку, але\(\int_{C_1} \vecs F·d\vecs r≠\int_{C_2} \vecs F·d\vecs r\). Тому не\(\vecs{F}\) є незалежним від шляху і не\(\vecs{F}\) є консервативним.

Підводячи підсумок:\(\vecs{F}\) задовольняє перехресне часткове властивість і все ж не\(\vecs{F}\) є консервативним. Що пішло не так? Чи суперечить це Перехресна часткова властивість консервативних векторних полів? Проблема полягає в тому, що домен\(\vecs{F}\) є все,\(ℝ^2\) крім походження. Іншими словами, домен\(\vecs{F}\) має дірку на початку, і тому домен не просто пов'язаний. Оскільки домен не просто пов'язаний, перехресна часткова властивість консервативних векторних полів не застосовується до\(\vecs{F}\).

Закриваємо цей розділ, розглядаючи приклад корисності фундаментальної теореми для лінійних інтегралів. Тепер, коли ми можемо перевірити, чи є векторне поле консервативним, ми завжди можемо вирішити, чи фундаментальна теорема для лінійних інтегралів може бути використана для обчислення інтеграла векторної лінії. Якщо нас просять обчислити інтеграл форми\(\int_C \vecs F·d\vecs r\), то першим нашим питанням має бути: Чи\(\vecs{F}\) консервативний? Якщо відповідь так, то ми повинні знайти потенційну функцію і використовувати фундаментальну теорему для лінійних інтегралів для обчислення інтеграла. Якщо відповідь ні, то фундаментальна теорема для лінійних інтегралів не може нам допомогти, і ми повинні використовувати інші методи, такі як використання методу з попереднього розділу (використовуючи\(\vecs F(\vecs r(t))\) і\(\vecs r'(t)\)).

Приклад\(\PageIndex{10}\): Using the Fundamental Theorem for Line Integrals

Обчислити\(C\) лінійний інтеграл\(\int_C \vecs F·d\vecs r\), де\(\vecs F(x,y,z)=⟨2xe^yz+e^xz,\,x^2e^yz,\,x^2e^y+e^x⟩\) і - будь-яка плавна крива, яка йде від початку до\((1,1,1)\).

Рішення

Перш ніж намагатися обчислити інтеграл, нам потрібно визначити, чи\(\vecs{F}\) є консервативним і чи просто\(\vecs{F}\) пов'язана область. Домен\(\vecs{F}\) - це все\(ℝ^3\), що пов'язано і не має отворів. Тому домен з\(\vecs{F}\) просто підключений. Нехай

\[P(x,y,z)=2xe^yz+e^xz, \;\; Q(x,y,z)=x^2e^yz, \;\; \text{and} \;\; R(x,y,z)=x^2e^y+e^x \nonumber \]

так що\(\vecs{F}(x,y,z)=⟨P,Q,R⟩\). Оскільки домен просто\(\vecs{F}\) пов'язаний, ми можемо перевірити перехресні частки, щоб визначити, чи\(\vecs{F}\) є консервативним. Зауважте, що

\[\begin{align*} P_y(x,y,z) &=2xe^yz=Q_x(x,y,z) \\[4pt]P_z(x,y,z) &=2xe^y+e^x=R_x(x,y,z) \\[4pt] Q_z(x,y,z) &=x^2e^y=R_y(x,y,z).\end{align*}\]

Тому\(\vecs{F}\) є консервативним.

Для оцінки з\(\int_C \vecs F·d\vecs r\) використанням фундаментальної теореми для лінійних інтегралів нам потрібно знайти потенційну функцію\(f\) для\(\vecs{F}\). \(f\)Дозволяти бути потенційною функцією для\(\vecs{F}\). Потім\(\vecs \nabla f=\vecs F\), і тому\(f_x(x,y,z)=2xe^yz+e^xz\). Інтеграція цього рівняння\(f(x,y,z)=x^2e^yz+e^xz+h(y,z)\) щодо\(x\) дає деяку функцію\(h\). Диференціювання цього рівняння щодо\(y\) дає\(x^2e^yz+h_y(y,z)=Q(x,y,z)=x^2e^yz\), що випливає\(h_y(y,z)=0\). Тому\(h\) є функцією\(z\) тільки, і\(f(x,y,z)=x^2e^yz+e^xz+h(z)\). Щоб знайти\(h\), зверніть увагу, що\(f_z=x^2e^y+e^x+h′(z)=R=x^2e^y+e^x\). Тому\(h′(z)=0\) і ми можемо взяти\(h(z)=0\). Потенційна функція для\(\vecs{F}\) є\(f(x,y,z)=x^2e^yz+e^xz\).

Тепер, коли у нас є потенційна функція, ми можемо використовувати фундаментальну теорему для лінійних інтегралів для оцінки інтеграла. За теоремою

\[\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \vecs \nabla f·d\vecs r\\[4pt] &=f(1,1,1)−f(0,0,0)\\[4pt] &=2e. \end{align*}\]

Аналіз

Зверніть увагу, що якби ми не визнали, що\(\vecs{F}\) є консервативним, нам довелося б параметризувати\(C\) та використовувати метод з попереднього розділу. Оскільки крива\(C\) невідома, використання фундаментальної теореми для лінійних інтегралів набагато простіше.

Вправа\(\PageIndex{9}\)

Обчислити інтеграл\(\int_C \vecs F·d\vecs r\), де\(\vecs{F}(x,y)=⟨\sin x\sin y, 5−\cos x\cos y⟩\) і\(C\) є півколом з початковою\((0,\pi)\) і кінцевою точкою\((0,−\pi)\).

Підказка

Використовуйте фундаментальну теорему для лінійних інтегралів.

Відповідь

\(−10\pi\)

Приклад\(\PageIndex{11}\): Work Done on a Particle

\(\vecs F(x,y)=⟨2xy^2,2x^2y⟩\)Дозволяти бути силовим полем. Припустимо, що частка починає свій рух біля початку і закінчує свій рух в будь-якій точці площини, яка не знаходиться на\(x\) -осі або\(y\) -осі. Крім того, рух частинки можна моделювати за допомогою плавної параметризації. Показати, що\(\vecs{F}\) робить позитивну роботу над частинкою.

Рішення

Ми показуємо, що\(\vecs{F}\) робить позитивну роботу над частинкою, показуючи, що\(\vecs{F}\) є консервативним, а потім за допомогою фундаментальної теореми для лінійних інтегралів.

Щоб показати,\(\vecs{F}\) що консервативно, припустимо,\(f(x,y)\) були потенційна функція для\(\vecs{F}\). Потім,\(\vecs \nabla f(x,y)=\vecs F(x,y)=⟨2xy^2,2x^2y⟩\) а значить\(f_x(x,y)=2xy^2\) і\(f_y(x,y)=2x^2y\). Рівняння\(fx(x,y)=2xy^2\) має на увазі це\(f(x,y)=x^2y^2+h(y)\). Виведення обох сторін щодо\(y\) врожайності\(f_y(x,y)=2x^2y+h′(y)\). Тому\(h′(y)=0\) і ми можемо взяти\(h(y)=0\).

Якщо\(f(x,y)=x^2y^2\), то зверніть увагу\(\vecs \nabla f(x,y)=⟨2xy^2,2x^2y⟩=\vecs F\), що, а значить\(f\) є потенційною функцією для\(\vecs{F}\).

\((a,b)\)Дозволяти точка, в якій частка зупиняється рух, і нехай\(C\) позначають криву, яка моделює рух частинки. Робота, виконана\(\vecs{F}\) над частинкою, є\(\int_C \vecs{F}·d\vecs{r}\). За фундаментальною теоремою для лінійних інтегралів

\[\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \nabla f·d\vecs r \\[4pt] &=f(a,b)−f(0,0)\\[4pt] &=a^2b^2. \end{align*}\]

Так як\(a≠0\) і\(b≠0\), за припущенням,\(a^2b^2>0\). \(\int_C \vecs F·d\vecs r>0\)Тому і\(\vecs{F}\) робить позитивну роботу над частинкою.

Аналіз

Зверніть увагу, що ця проблема була б набагато складнішою без використання фундаментальної теореми для лінійних інтегралів. Щоб застосувати вивчені нами інструменти, нам потрібно було б дати криву параметризацію та використовувати метод з попереднього розділу. Оскільки шлях руху\(C\) може бути настільки екзотичним, наскільки ми хочемо (поки він гладкий), параметризувати рух частинки може бути дуже важко.

Вправа\(\PageIndex{10}\)

Нехай\(\vecs{F}(x,y)=⟨4x^3y^4,4x^4y^3⟩\), і припустимо, що частка рухається від точки\((4,4)\) до\((1,1)\) уздовж будь-якої плавної кривої. Робиться робота над частинкою позитивною, негативною або нульовою?\(\vecs{F}\)

Підказка

Використовуйте фундаментальну теорему для лінійних інтегралів.

Відповідь

Негативний

Ключові концепції

• Теореми в цьому розділі вимагають кривих, які є замкнутими, простими або обома, і областей, які з'єднані або просто з'єднані.
• Лінійний інтеграл консервативного векторного поля можна обчислити за допомогою Фундаментальної теореми для лінійних інтегралів. Ця теорема є узагальненням фундаментальної теореми числення у вищих вимірах. Використання цієї теореми зазвичай полегшує обчислення лінійного інтеграла.
• Консервативні поля не залежать від шляху. Лінійний інтеграл консервативного поля залежить тільки від значення потенційної функції в кінцевих точках доменної кривої.
• Задане векторне поле\(\vecs{F}\), ми можемо перевірити, чи\(\vecs{F}\) є консервативним, використовуючи перехресну часткову властивість. Якщо\(\vecs{F}\) має перехресне часткове властивість і домен просто пов'язаний, то\(\vecs{F}\) консервативний (і, таким чином, має потенційну функцію). Якщо\(\vecs{F}\) консервативний, ми можемо знайти потенційну функцію, використовуючи Стратегію вирішення проблем.
• Циркуляція консервативного векторного поля на просто пов'язаній області по замкнутій кривій дорівнює нулю.

Ключові рівняння

• Фундаментальна теорема для лінійних інтегралів
  \(\displaystyle \int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a))\)
• Циркуляція консервативного поля над кривою С, що охоплює просто пов'язану область
  \(\displaystyle \oint_C \vecs \nabla f·d\vecs r=0\)

Глосарій

замкнута крива

крива, яка починається і закінчується в одній точці

підключений регіон

область, в якій будь-які дві точки можуть бути з'єднані шляхом з трасою, що міститься повністю всередині області

Фундаментальна теорема для лінійних інтегралів

значення лінійного інтеграла\(\displaystyle \int_C\vecs ∇f⋅d\vecs r\) залежить тільки від значення\(f\) в кінцевих точках\(C: \displaystyle \int_C \vecs ∇f⋅d\vecs r=f(\vecs r(b))−f(\vecs r(a))\)

незалежність шляху

векторне поле\(\vecs{F}\) має незалежність від шляху, якщо\(\displaystyle \int_{C_1} \vecs F⋅d\vecs r=\displaystyle \int_{C_2} \vecs F⋅d\vecs r\) для будь-яких кривих\(C_1\) і\(C_2\) в області\(\vecs{F}\) з однаковими початковими точками і кінцевими точками

проста крива

крива, яка не перетинається

просто підключений регіон

область, яка пов'язана і має властивість, що будь-яка замкнута крива, яка повністю лежить всередині області, охоплює точки, які повністю знаходяться всередині області