16.6: Поверхневі інтеграли
- Page ID
- 62259
- Знайдіть параметричні зображення циліндра, конуса та сфери.
- Опишіть поверхневий інтеграл скалярно-значної функції над параметричною поверхнею.
- Використовуйте інтеграл поверхні для обчислення площі даної поверхні.
- Поясніть значення орієнтованої поверхні, наводячи приклад.
- Опишіть поверхневий інтеграл векторного поля.
- Використовуйте поверхневі інтеграли для вирішення прикладних задач.
Ми бачили, що лінійний інтеграл є інтегралом над шляхом в площині або в просторі. Однак, якщо ми хочемо інтегрувати над поверхнею (двовимірним об'єктом), а не шляхом (одновимірним об'єктом) у просторі, то нам потрібен новий вид інтеграла, який може обробляти інтеграцію над об'єктами у вищих вимірах. Ми можемо розширити концепцію лінійного інтеграла до поверхневого інтеграла, щоб дозволити нам виконати цю інтеграцію.
Поверхневі інтеграли важливі з тих же причин, що і лінійні інтеграли важливі. Вони мають багато застосувань до фізики та техніки, і вони дозволяють нам розробляти вищі розмірні версії Фундаментальної теореми обчислення. Зокрема, поверхневі інтеграли дозволяють узагальнити теорему Гріна до більш високих вимірів, і вони з'являються в деяких важливих теоремах, які ми обговорюємо в наступних розділах.
Параметричні поверхні
Поверхневий інтеграл схожий на лінійний інтеграл, за винятком того, що інтеграція виконується над поверхнею, а не контуром. У цьому сенсі поверхневі інтеграли розширюються при вивченні лінійних інтегралів. Подібно до лінійних інтегралів, існує два види поверхневих інтегралів: поверхневий інтеграл скалярно-значної функції та поверхневий інтеграл векторного поля.
Однак, перш ніж ми зможемо інтегруватися над поверхнею, нам потрібно розглянути саму поверхню. Нагадаємо, що для обчислення скалярного або векторного інтеграла\(C\) прямої над кривою спочатку потрібно параметризувати\(C\). Аналогічним чином, щоб обчислити поверхневий інтеграл над поверхнею\(S\), нам потрібно параметризувати\(S\). Тобто нам потрібна робоча концепція параметризованої поверхні (або параметричної поверхні), так само, як у нас вже є поняття параметризованої кривої.
Параметризована поверхня дається описом форми
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
Зверніть увагу, що ця параметризація включає два параметри\(v\),\(u\) і, оскільки поверхня двовимірна, і тому для простеження поверхні потрібні дві змінні. Параметри\(u\) і\(v\) змінюються в області, яка називається доменом параметру, або простором параметрів —множина точок у\(uv\) -plane, на яку можна замінити\(\vecs r\). Кожен вибір\(u\) і\(v\) в області параметрів дає точку на поверхні, так само як кожен вибір параметра\(t\) дає точку на параметризованій кривій. Вся поверхня створюється шляхом здійснення всіх можливих варіантів\(u\) і\(v\) над доменом параметрів.
Задано параметризацію поверхні
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
область параметра параметризації - це множина точок у\(uv\) -площині, на які можна підставити\(\vecs r\).
Опишіть поверхню,\(S\) параметризовану
\[\vecs{r}(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, -\infty < u < \infty, \, -\infty < v < \infty. \nonumber \]
Рішення
Щоб отримати уявлення про форму поверхні, спочатку намічаємо деякі точки. Оскільки параметр domain - це все\(\mathbb{R}^2\), ми можемо вибрати будь-яке значення для u та v і побудувати відповідну точку. Якщо\(u = v = 0\), то\(\vecs r(0,0) = \langle 1,0,0 \rangle\), так точка (1, 0, 0) знаходиться на\(S\). Аналогічно точки\(\vecs r(\pi, 2) = (-1,0,2)\) і\(\vecs r \left(\dfrac{\pi}{2}, 4\right) = (0,1,4)\) знаходяться на\(S\).
Хоча побудова точок може дати нам уявлення про форму поверхні, нам зазвичай потрібно досить багато точок, щоб побачити форму. Оскільки для побудови десятків або сотень балів потрібно багато часу, ми використовуємо іншу стратегію. Для візуалізації\(S\) ми візуалізуємо дві сім'ї кривих, які лежать на\(S\). У першому сімействі кривих ми тримаємо\(u\) постійною; у другому сімействі кривих ми тримаємо\(v\) постійною. Це дозволяє побудувати «скелет» поверхні, тим самим отримуючи уявлення про її формі.
- Припустимо, що\(u\) це константа\(K\). Потім крива, промальована параметризацією є\(\langle \cos K, \, \sin K, \, v \rangle \), яка дає вертикальну лінію, яка проходить через точку\((\cos K, \sin K, v \rangle\) в\(xy\) -площині.
- Припустимо, що\(v\) це константа\(K\). Потім крива, промальована параметризацією\(\langle \cos u, \, \sin u, \, K \rangle \), є, що дає коло в площині\(z = K\) з радіусом 1 і центром\((0, 0, K)\).
Якщо\(u\) утримується постійною, то отримуємо вертикальні лінії; якщо\(v\) утримується постійною, то отримуємо кола радіуса 1 по центру навколо вертикальної лінії, яка йде через початок. Тому поверхня, промальована параметризацією, - циліндрична\(x^2 + y^2 = 1\) (рис.\(\PageIndex{1}\)).
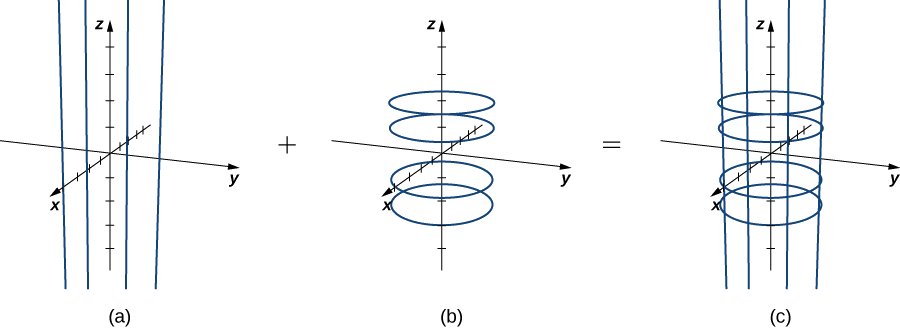
Зверніть увагу, що якщо\(x = \cos u\) і\(y = \sin u\), то\(x^2 + y^2 = 1\), так точки з S дійсно лежать на циліндрі. І навпаки, кожна точка на циліндрі міститься в якомусь колі\(\langle \cos u, \, \sin u, \, k \rangle \) для деяких\(k\), а тому кожна точка на циліндрі міститься в параметризованої поверхні (рис.\(\PageIndex{2}\)).
Аналіз
Зверніть увагу, що якщо ми змінимо домен параметра, ми могли б отримати іншу поверхню. Наприклад, якщо ми обмежили домен\(0 \leq u \leq \pi, \, -\infty < v < 6\), то поверхня буде півциліндра висотою 6.
Опишіть поверхню з параметризацією
\[\vecs{r} (u,v) = \langle 2 \, \cos u, \, 2 \, \sin u, \, v \rangle, \, 0 \leq u \leq 2\pi, \, -\infty < v < \infty \nonumber \]
- Підказка
-
Тримайте\(u\) і\(v\) постійно, і подивіться, які криві результату.
- Відповідь
-
Циліндр\(x^2 + y^2 = 4\)
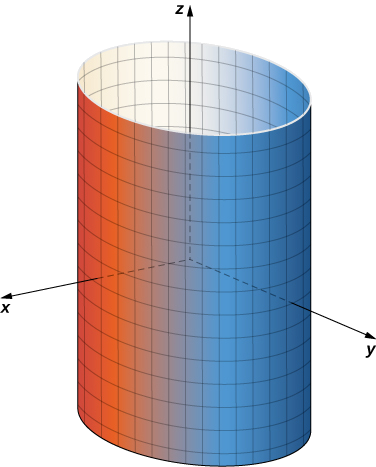
Дайте параметризацію конуса,\(x^2 + y^2 = z^2\) що лежить на площині або над нею\(z = -2\).
Рішення
Горизонтальний перетин конуса по висоті\(z = u\) - коло\(x^2 + y^2 = u^2\). Тому точка на конусі на висоті\(u\) має координати\((u \, \cos v, \, u \, \sin v, \, u)\) для кута\(v\). Значить, параметризація конуса є\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle \). Так як нас цікавить не весь конус, а тільки ділянка на площині або над\(z = -2\) нею, область параметра задається\(-2 < u < \infty, \, 0 \leq v < 2\pi\) (рис.\(\PageIndex{4}\)).
Дайте параметризацію для ділянки конуса,\(x^2 + y^2 = z^2\) що лежить в першому октанті.
- Підказка
-
Розглянемо область параметра для цієї поверхні.
- Відповідь
-
\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, 0 < u < \infty, \, 0 \leq v < \dfrac{\pi}{2}\)
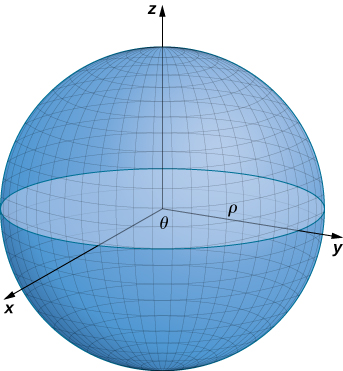
Ми обговорили параметризації різних поверхонь, але окремого обговорення потребують два важливих типи поверхонь: сфери та графіки двозмінних функцій. Для параметризації сфери найпростіше використовувати сферичні координати. Сфера радіуса,\(\rho\) центрована на початку, задається параметризацією
\(\vecs r(\phi,\theta) = \langle \rho \, \cos \theta \, \sin \phi, \, \rho \, \sin \theta \, \sin \phi, \, \rho \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi.\)
Ідея цієї параметризації полягає в тому, що,\(\phi\) коли змітає вниз від позитивної\(z\) -осі, коло радіуса\(\rho \, \sin \phi\) простежується шляхом\(\theta\) запуску від 0 до\(2\pi\). Щоб переконатися в цьому, нехай\(\phi\) буде виправлено. Тоді
\ [\ begin {align*} x^2 + y^2 &= (\ rho\,\ cos\ тета\,\ sin\ phi) ^2 + (\ rho\,\ тета\,\ sin\ phi) ^2\\ [4pt]
&=\ rho^2\ sin^2\ phi (\ cos^2\ тета +\ sin^2\ тета)\\ pt]
&=\ rho^2\,\ sin^2\ phi\\ [4pt]
&= (\ rho\,\ sin\ phi) ^2. \ end {вирівнювати*}\]
Це призводить до отримання потрібного кола (рис.\(\PageIndex{5}\)).
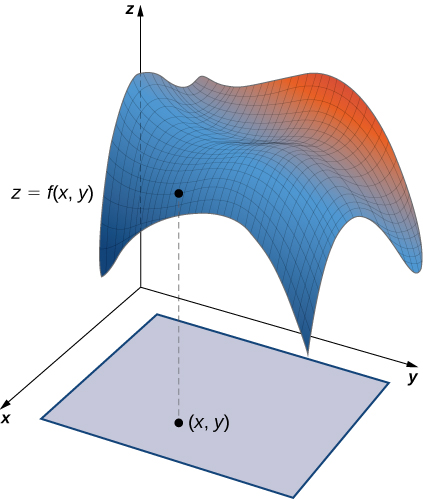
Нарешті, щоб параметризувати графік двозмінної функції, ми спочатку дозволимо\(z = f(x,y)\) бути функцією двох змінних. Найпростіша параметризація графа\(f\) є\(\vecs r(x,y) = \langle x,y,f(x,y) \rangle\), де\(x\) і\(y\) варіюються по області\(f\) (рис.\(\PageIndex{6}\)). Наприклад, графік\(f(x,y) = x^2 y\) може бути параметризований тим\(\vecs r(x,y) = \langle x,y,x^2y \rangle\), де параметри\(x\) і\(y\) змінюються по області\(f\). Якщо ми дбаємо лише про шматок графіка\(f\) - скажімо, шматок графіка над прямокутником\([ 1,3] \times [2,5]\) - то ми можемо обмежити область параметра, щоб дати цей шматок поверхні:
\[\vecs r(x,y) = \langle x,y,x^2y \rangle, \, 1 \leq x \leq 3, \, 2 \leq y \leq 5. \nonumber \]
Аналогічно, якщо\(S\) це поверхня, задана рівнянням\(x = g(y,z)\) або рівнянням\(y = h(x,z)\), то параметризація\(S\) є\(\vecs r(y,z) = \langle g(y,z), \, y,z\rangle\) або\(\vecs r(x,z) = \langle x,h(x,z), z\rangle\), відповідно. Наприклад, графік параболоїда\(2y = x^2 + z^2\) можна параметризувати по\(\vecs r(x,y) = \left\langle x, \dfrac{x^2+z^2}{2}, z \right\rangle, \, 0 \leq x < \infty, \, 0 \leq z < \infty\). Зверніть увагу, що нам не потрібно варіюватися по всій області\(y\) тому, що\(x\) і\(z\) знаходяться в квадраті.
Давайте тепер узагальнимо поняття гладкості і регулярності до параметричної поверхні. Нагадаємо, що крива параметризація\(\vecs r(t), \, a \leq t \leq b\) є регулярною (або гладкою), якщо\(\vecs r'(t) \neq \vecs 0\) для всіх\(t\) в\([a,b]\). Для кривої ця умова гарантує, що зображення\(\vecs r\) дійсно є кривою, а не просто точкою. Для прикладу розглянемо параметризацію кривої\(\vecs r(t) = \langle 1,2\rangle, \, 0 \leq t \leq 5\). Зображення цієї параметризації просто точка\((1,2)\), яка не є кривою. Зауважте також, що\(\vecs r'(t) = \vecs 0\). Той факт, що похідна є нульовим вектором вказує на те, що ми насправді не дивимося на криву.
Аналогічно, ми хотіли б поняття регулярності (або гладкості) для поверхонь, так що параметризація поверхні дійсно простежує поверхню. Для мотивації визначення закономірності параметризації поверхні розглянемо параметризацію
\[\vecs r(u,v) = \langle 0, \, \cos v, \, 1 \rangle, \, 0 \leq u \leq 1, \, 0 \leq v \leq \pi. \nonumber \]
Хоча ця параметризація, здається, є параметризацією поверхні, зверніть увагу, що зображення насправді є лінією (рис.\(\PageIndex{7}\)). Як ми могли уникнути таких параметризацій? Параметризації, які не дають реальної поверхні? Зверніть увагу, що\(\vecs r_u = \langle 0,0,0 \rangle\) і\(\vecs r_v = \langle 0, -\sin v, 0\rangle\), і відповідний перехресний добуток дорівнює нулю. Аналогом умови\(\vecs r'(t) = \vecs 0\) є те, що не\(\vecs r_u \times \vecs r_v\) дорівнює нулю для точки\((u,v)\) в області параметрів, яка є регулярною параметризацією.
Параметризація\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) - це регулярна параметризація, якщо не\(\vecs r_u \times \vecs r_v\) дорівнює нулю для точки\((u,v)\) в області параметрів.
Якщо параметризація\(\vec{r}\) регулярна, то зображення\(\vec{r}\) є двовимірним об'єктом, як і повинна бути поверхня. Протягом цієї глави передбачається, що параметризації\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) є регулярними.
Нагадаємо, що крива параметризація\(\vecs r(t), \, a \leq t \leq b\) плавна, якщо\(\vecs r'(t)\) є безперервною і\(\vecs r'(t) \neq \vecs 0\) для всіх\(t\) в\([a,b]\). Неофіційно параметризація кривої плавна, якщо отримана крива не має гострих кутів. Визначення параметризації гладкої поверхні аналогічно. Неофіційно параметризація поверхні є гладкою, якщо отримана поверхня не має гострих кутів.
Параметризація поверхні\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) є гладкою, якщо вектор не\(\vecs r_u \times \vecs r_v\) дорівнює нулю для будь-якого вибору\(u\) і\(v\) в області параметрів.
Поверхня також може бути кусково гладкою, якщо вона має гладкі грані, але також має місця, де спрямованих похідних не існує.
Яка з фігур на малюнку\(\PageIndex{8}\) гладка?

Рішення
Поверхня на малюнку\(\PageIndex{8a}\) може бути параметризована
\[\vecs r(u,v) = \langle (2 + \cos v) \cos u, \, (2 + \cos v) \sin u, \, \sin v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v < 2\pi \nonumber \]
(ми можемо використовувати технологію для перевірки). Зверніть увагу, що вектори
\[\vecs r_u = \langle - (2 + \cos v)\sin u, \, (2 + \cos v) \cos u, 0 \rangle \nonumber \]
і
\[\vecs r_v = \langle -\sin v \, \cos u, \, - \sin v \, \sin u, \, \cos v \rangle \nonumber \]
існує для будь-якого вибору\(u\) і\(v\) в області параметрів, і
\[ \begin{align*} \vecs r_u \times \vecs r_v &= \begin{vmatrix} \mathbf{\hat{i}}& \mathbf{\hat{j}}& \mathbf{\hat{k}} \\ -(2 + \cos v)\sin u & (2 + \cos v)\cos u & 0\\ -\sin v \, \cos u & - \sin v \, \sin u & \cos v \end{vmatrix} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [2 + \cos v) \sin u \, \cos v] \mathbf{\hat{j}} + [(2 + \cos v)\sin v \, \sin^2 u + (2 + \cos v) \sin v \, \cos^2 u]\mathbf{\hat{k}} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [(2 + \cos v) \sin u \, \cos v]\mathbf{\hat{j}} + [(2 + \cos v)\sin v ] \mathbf{\hat{k}}. \end{align*}\]
\(\mathbf{\hat{k}}\)Складова цього вектора дорівнює нулю, тільки якщо\(v = 0\) або\(v = \pi\). Якщо\(v = 0\) або\(v = \pi\), то єдиним вибором для\(u\) цього є нульовий\(\mathbf{\hat{j}}\) компонент\(u = 0\) або\(u = \pi\). Але, ці варіанти не\(u\) роблять\(\mathbf{\hat{i}}\) компонент нульовим. Тому не\(\vecs r_u \times \vecs r_v\) дорівнює нулю для будь-якого вибору\(u\) і\(v\) в області параметрів, а параметризація проходить плавно. Зверніть увагу, що відповідна поверхня не має гострих кутів.
У піраміді на малюнку\(\PageIndex{8b}\) різкість кутів гарантує, що спрямовані похідні не існують у цих місцях. Тому піраміда не має плавної параметризації. Однак піраміда складається з чотирьох гладких граней, і при цьому ця поверхня кусково гладка.
Чи\(\vecs r(u,v) = \langle u^{2v}, v + 1, \, \sin u \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3\) гладка параметризація поверхні?
- Підказка
-
Дослідіть перехресний твір\(\vecs r_u \times \vecs r_v\).
- Відповідь
-
Так
Площа поверхні параметричної поверхні
Наша мета - визначити поверхневий інтеграл, і в якості першого кроку ми розглянули, як параметризувати поверхню. Другий крок - визначення площі поверхні параметричної поверхні. Позначення, необхідні для розробки цього визначення, використовуються протягом всієї іншої частини цієї глави.
\(S\)Дозволяти поверхню з параметризацією\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) над деяким параметром області\(D\). Ми припускаємо, що поверхнева параметризація\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) є безперервно диференційованою, тобто кожна компонентна функція має неперервні часткові похідні. Припустімо, для простоти, що\(D\) це прямокутник (хоча наступний матеріал може бути розширено для обробки непрямокутних доменів параметрів). \(D\)Розділіть прямокутник на підпрямокутники\(D_{ij}\) з горизонтальною шириною\(\Delta u\) і вертикальною довжиною\(\Delta v\). Припустимо, що i коливається від 1 до m, а j коливається від 1 до n так, що\(D\) підрозділяється на mn прямокутників. Це\(D\) поділ на підпрямокутники дає відповідне поділ поверхні\(S\) на шматки\(S_{ij}\). Виберіть точку\(P_{ij}\) в кожному шматку\(S_{ij}\). Точка\(P_{ij}\) відповідає точці\((u_i, v_j)\) в області параметра.
Зверніть увагу, що ми можемо сформувати сітку з лініями, паралельними\(u\) -осі та\(v\) -осі в\(uv\) -площині. Ці лінії сітки відповідають набору кривих сітки на поверхні\(S\), які параметризуються\(\vecs r(u,v)\). Без втрати спільності припустимо, що\(P_{ij}\) знаходиться в куті дві криві сітки, як на рис\(\PageIndex{9}\). Якщо ми думаємо про\(\vecs r\) відображення від\(uv\) -plane до\(\mathbb{R}^3\), криві сітки є зображенням ліній сітки під\(\vecs r\). Щоб бути точним, розглянемо лінії сітки, які проходять через точку\((u_i, v_j)\). Один рядок\(x = u_i, \, y = v\) задається, інший задається\(x = u, \, y = v_j\). У першій лінії сітки горизонтальна складова утримується постійною, що дає вертикальну лінію\((u_i, v_j)\). У другій лінії сітки вертикальна складова утримується постійною, даючи горизонтальну лінію наскрізь\((u_i, v_j)\). Відповідні криві сітки є\(\vecs r(u_i, v)\) і,\((u, v_j)\) і ці криві перетинаються в точці\(P_{ij}\).
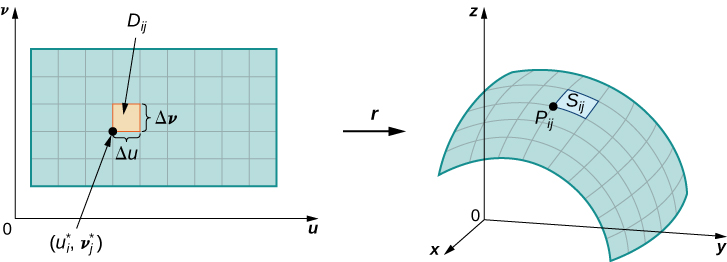
Тепер розглянемо вектори, дотичні до цих кривих сітки. Для кривої\(\vecs r(u_i,v)\) сітки вектор дотичної точки\(P_{ij}\) дорівнює
\[\vecs t_v (P_{ij}) = \vecs r_v (u_i,v_j) = \langle x_v (u_i,v_j), \, y_v(u_i,v_j), \, z_v (u_i,v_j) \rangle. \nonumber \]
Для кривої\(\vecs r(u, v_j)\) сітки вектор дотичної точки\(P_{ij}\) дорівнює
\[\vecs t_u (P_{ij}) = \vecs r_u (u_i,v_j) = \langle x_u (u_i,v_j), \, y_u(u_i,v_j), \, z_u (u_i,v_j) \rangle. \nonumber \]
Якщо вектор\(\vecs N = \vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})\) існує і не дорівнює нулю, то дотична площина при\(P_{ij}\) існує (рис.\(\PageIndex{10}\)). Якщо шматок\(S_{ij}\) досить малий, то дотична площина в точці\(P_{ij}\) є хорошим наближенням шматка\(S_{ij}\).
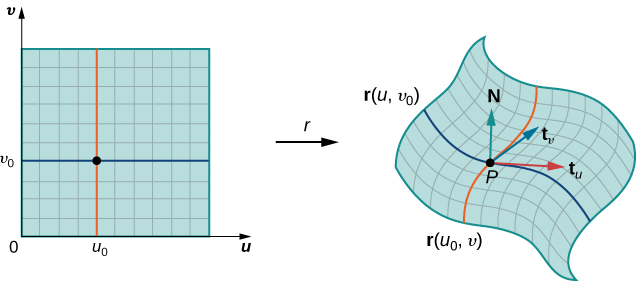
Дотична площина в\(P_{ij}\) містить вектори\(\vecs t_u(P_{ij})\)\(\vecs t_v(P_{ij})\) і, отже, паралелограм, що охоплюється\(\vecs t_u(P_{ij})\) і\(\vecs t_v(P_{ij})\) знаходиться в дотичній площині. Оскільки вихідний прямокутник у\(uv\) -площині, що відповідає\(S_{ij}\) має ширину\(\Delta u\) та довжину\(\Delta v\), паралелограм, який ми використовуємо для наближення,\(S_{ij}\) є паралелограмом, що охоплюється\(\Delta u \vecs t_u(P_{ij})\) і\(\Delta v \vecs t_v(P_{ij})\). Іншими словами, ми масштабуємо дотичні вектори за константами\(\Delta u\) і\(\Delta v\) відповідаємо масштабу вихідного поділу прямокутників в області параметрів. Тому площа паралелограма, яка використовується для наближення площі,\(S_{ij}\) дорівнює
\[\Delta S_{ij} \approx ||(\Delta u \vecs t_u (P_{ij})) \times (\Delta v \vecs t_v (P_{ij})) || = ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij}) || \Delta u \,\Delta v. \nonumber \]
Зміна точки\(P_{ij}\) над усіма шматками\(S_{ij}\) і попереднє наближення призводить до наступного визначення площі поверхні параметричної поверхні (рис.\(\PageIndex{11}\)).
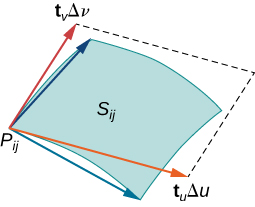
Нехай\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) з параметром домену\(D\) буде плавна параметризація поверхні\(S\). Крім того, припустимо,\(S\) що простежується лише один раз, коли\((u,v)\) змінюється\(D\). Площа поверхні\(S\) є
\[\iint_D ||\vecs t_u \times \vecs t_v || \,dA, \label{equation1} \]
де\(\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\)
і
\[\vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
Обчисліть площу бічної поверхні (площа «боку», не включаючи підставу) правого круглого конуса висотою h і радіусом r.
Рішення
Перш ніж обчислити площу поверхні цього конуса за допомогою Equation\ ref {equation1}, нам потрібна параметризація. Ми припускаємо, що цей\(\mathbb{R}^3\) конус знаходиться в з його вершиною біля початку (рис.\(\PageIndex{12}\)). Для отримання параметризації,\(\alpha\) нехай кут, який змітається, починаючи з позитивного z -осі і закінчуючи на конусі, і нехай\(k = \tan \alpha\). Для значення висоти\(v\) з радіус кола\(0 \leq v \leq h\), утвореного перетином конуса з площиною,\(z = v\) дорівнює\(kv\). Тому параметризація цього конуса полягає в
\[\vecs s(u,v) = \langle kv \, \cos u, \, kv \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h. \nonumber \]
Ідея цієї параметризації полягає в тому, що для фіксованого\(v\) -значення коло змітається, дозволяючи\(u\) варіювати коло на висоті\(v\) та радіусі\(kv\). У міру\(v\) збільшення параметризація змітає «стопку» кіл, в результаті чого виходить потрібний конус.
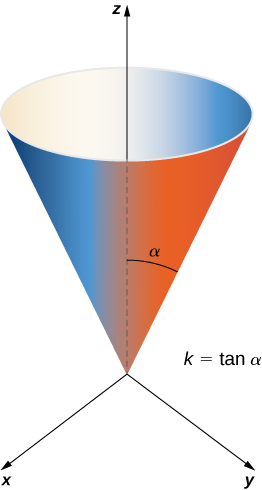
З параметризацією в руці ми можемо обчислити площу поверхні конуса за допомогою Equation\ ref {equation1}. Дотичними векторами є\(\vecs t_u = \langle - kv \, \sin u, \, kv \, \cos u, \, 0 \rangle\) і\(\vecs t_v = \langle k \, \cos u, \, k \, \sin u, \, 1 \rangle\). Тому,
\[ \begin{align*} \vecs t_u \times \vecs t_v &= \begin{vmatrix} \mathbf{\hat{i}} & \mathbf{\hat{j}} & \mathbf{\hat{k}} \\ -kv \sin u & kv \cos u & 0 \\ k \cos u & k \sin u & 1 \end{vmatrix} \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \, \sin^2 u - k^2 v \, \cos^2 u \rangle \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, - k^2 v \rangle. \end{align*}\]
Величина цього вектора дорівнює
\[ \begin{align*} ||\langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \rangle || &= \sqrt{k^2 v^2 \cos^2 u + k^2 v^2 \sin^2 u + k^4v^2} \\[4pt] &= \sqrt{k^2v^2 + k^4v^2} \\[4pt] &= kv\sqrt{1 + k^2}. \end{align*}\]
За рівнянням\ ref {equation1} площа поверхні конуса дорівнює
\[ \begin{align*}\iint_D ||\vecs t_u \times \vecs t_v|| \, dA &= \int_0^h \int_0^{2\pi} kv \sqrt{1 + k^2} \,du\, dv \\[4pt] &= 2\pi k \sqrt{1 + k^2} \int_0^h v \,dv \\[4pt] &= 2 \pi k \sqrt{1 + k^2} \left[\dfrac{v^2}{2}\right]_0^h \\[4pt] \\[4pt] &= \pi k h^2 \sqrt{1 + k^2}. \end{align*}\]
З тих пір\(k = \tan \alpha = r/h\),
\[ \begin{align*} \pi k h^2 \sqrt{1 + k^2} &= \pi \dfrac{r}{h}h^2 \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] &= \pi r h \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] \\[4pt] &= \pi r \sqrt{h^2 + h^2 \left(\dfrac{r^2}{h^2}\right) } \\[4pt] &= \pi r \sqrt{h^2 + r^2}. \end{align*}\]
Тому площа бічної поверхні конуса дорівнює\(\pi r \sqrt{h^2 + r^2}\).
АналізПлоща поверхні правого кругового конуса з радіусом\(r\) і висотою зазвичай\(h\) задається як\(\pi r^2 + \pi r \sqrt{h^2 + r^2}\). Причиною цього є те, що кругла основа включається як частина конуса, і тому площа підстави\(\pi r^2\) додається до площі бічної поверхні\(\pi r \sqrt{h^2 + r^2}\), яку ми знайшли.
Знайти площу поверхні поверхні з параметризацією\(\vecs r(u,v) = \langle u + v, \, u^2, \, 2v \rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 2\).
- Підказка
-
Використовуйте рівняння\ ref {equation1}.
- Відповідь
-
\(\≈ 43.02\)
Покажіть, що площа поверхні сфери\(x^2 + y^2 + z^2 = r^2\) є\(4 \pi r^2\).
Рішення
Сфера має параметризацію
\(r \, \cos \theta \, \sin \phi, \, r \, \sin \theta \, \sin \phi, \, r \, \cos \phi \rangle, \, 0 \leq \theta < 2\pi, \, 0 \leq \phi \leq \pi.\)
Дотичні вектори
\(\vecs t_{\theta} = \langle -r \, \sin \theta \, \sin \phi, \, r \, \cos \theta \, \sin \phi, \, 0 \rangle\)
і
\(\vecs t_{\phi} = \langle r \, \cos \theta \, \cos \phi, \, r \, \sin \theta \, \cos \phi, \, -r \, \sin \phi \rangle.\)
Тому,
\[ \begin{align*}\vecs t_{\phi} \times \vecs t_{\theta} &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin^2 \theta \, \sin \phi \, \cos \phi + r^2 \cos^2 \theta \, \sin \phi \, \cos \phi \rangle \\[4pt] &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin \phi \, \cos \phi \rangle. \end{align*}\]
Тепер,
\[ \begin{align*}||\vecs t_{\phi} \times \vecs t_{\theta} || &= \sqrt{r^4\sin^4\phi \, \cos^2 \theta + r^4 \sin^4 \phi \, \sin^2 \theta + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= \sqrt{r^4 \sin^4 \phi + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= r^2 \sqrt{\sin^2 \phi} \\[4pt] &= r \, \sin \phi.\end{align*}\]
Зверніть увагу, що\(\sin \phi \geq 0\) на області параметра тому що\(0 \leq \phi < \pi\), і це виправдовує рівняння\(\sqrt{\sin^2 \phi} = \sin \phi\). Площа поверхні сфери дорівнює
\[\int_0^{2\pi} \int_0^{\pi} r^2 \sin \phi \, d\phi \,d\theta = r^2 \int_0^{2\pi} 2 \, d\theta = 4\pi r^2. \nonumber \]
Отримано звичну формулу для площі поверхні сфери з використанням поверхневих інтегралів.
Показати, що площа поверхні циліндра\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\) є\(2\pi rh\). Зверніть увагу, що цей циліндр не включає верхній і нижній кола.
- Підказка
-
Скористайтеся стандартною параметризацією циліндра і дотримуйтесь попереднього прикладу.
- Відповідь
-
При стандартній параметризації циліндра Equation\ ref {equation1} показує, що площа поверхні дорівнює\(2 \pi rh\).
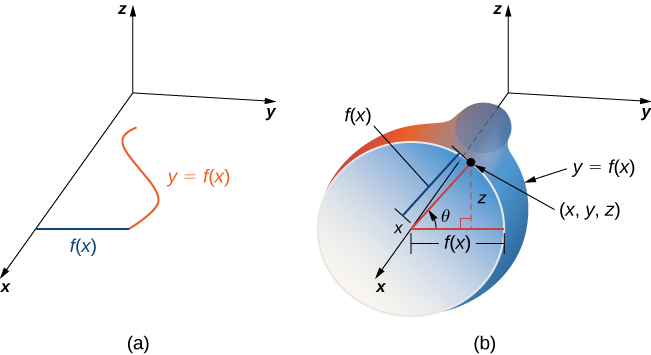
Окрім параметризації поверхонь, заданих рівняннями або стандартними геометричними формами, такими як конуси та сфери, ми також можемо параметризувати поверхні обертання. Тому ми можемо обчислити площу поверхні обертання за допомогою тих же прийомів. \(y = f(x) \geq 0\)Дозволяти позитивна однозмінна функція на області\(a \leq x \leq b\) і\(S\) нехай поверхню, отримана обертанням\(f\) навколо\(x\) -осі (рис.\(\PageIndex{13}\)). \(\theta\)Дозволяти буде кут повороту. Потім,\(S\) можуть бути параметризовані з\(\theta\) параметрами\(x\) і
\[\vecs r(x, \theta) = \langle x, f(x) \, \cos \theta, \, f(x) \sin \theta \rangle, \, a \leq x \leq b, \, 0 \leq x \leq 2\pi. \nonumber \]
Знайдіть площу поверхні обертання, отриманої при обертанні\(y = x^2, \, 0 \leq x \leq b\) навколо осі х (рис.\(\PageIndex{14}\)).
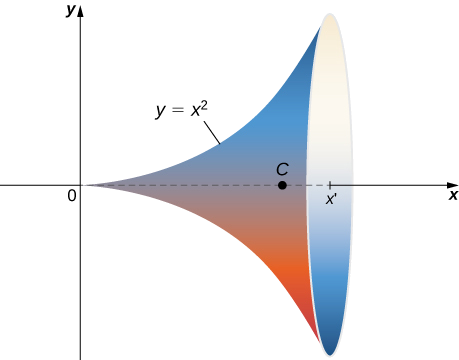
Рішення
Ця поверхня має параметризацію\(\vecs r(x, \theta) = \langle x, \, x^2 \cos \theta, \, x^2 \sin \theta \rangle, \, 0 \leq x \leq b, \, 0 \leq x < 2\pi.\)
Дотичними векторами є\( \vecs t_x = \langle 1, \, 2x \, \cos \theta, \, 2x \, \sin \theta \rangle\) і\(\vecs t_{\theta} = \langle 0, \, -x^2 \sin \theta, \, -x^2 \cos \theta \rangle\).
Тому,
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \langle 2x^3 \cos^2 \theta + 2x^3 \sin^2 \theta, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \\[4pt] &= \langle 2x^3, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \end{align*}\]
і
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \sqrt{4x^6 + x^4\cos^2 \theta + x^4 \sin^2 \theta} \\[4pt] &= \sqrt{4x^6 + x^4} \\[4pt] &= x^2 \sqrt{4x^2 + 1} \end{align*}\]
Площа поверхні обертання дорівнює
\ [\ почати {align*}\ int_0^b\ int_0^ {2\ pi} x^2\ sqrt {4x^2 + 1}\, d\ тета\, дх &= 2\ пі\ int_0^b x^2\ sqrt {4x^2 + 1}\, dx\\ [4pt]
&= 2\ пі\ ліворуч [\ dfrac {1} {64}\ ліворуч (2\ sqrt {4x^2 + 1} (8x^3+ x)\,\ sinh^ {-1} (2x)\ праворуч)\ праворуч] _0^b\\ [4pt]
&= 2\ пі\ ліворуч [\ dfrac {1} {64}\ ліворуч (2) \ sqrt {4b^2+ 1} (8b^3+ b)\,\ sinh^ {-1} (2b)\ праворуч)\ праворуч]. \ end {вирівнювати*}\]
Використовуйте Equation\ ref {equation1}, щоб знайти площу поверхні обертання, отриманої при обертанні кривої\(y = \sin x, \, 0 \leq x \leq \pi\) навколо\(x\) -осі.
- Підказка
-
Використовуйте параметризацію поверхонь обертання, наведену перед прикладом\(\PageIndex{7}\).
- Відповідь
-
\(2\pi (\sqrt{2} + \sinh^{-1} (1))\)
Поверхневий інтеграл скалярно-значної функції
Тепер, коли ми можемо параметризувати поверхні і ми можемо обчислити їх площу поверхні, ми можемо визначити поверхневі інтеграли. Спочатку розглянемо поверхневий інтеграл скалярно-значної функції. Неформально поверхневий інтеграл скалярно-значної функції є аналогом скалярного лінійного інтеграла в одному вищому вимірі. Область інтегрування скалярного лінійного інтеграла - параметризована крива (одновимірний об'єкт); областю інтеграції скалярного поверхневого інтеграла є параметризована поверхня (двовимірний об'єкт). Тому визначення поверхневого інтеграла слід за визначенням лінійного інтеграла досить тісно. Для скалярних лінійних інтегралів ми розрізали криву області на крихітні шматочки, обрали точку в кожному фрагменті, обчислили функцію в цій точці і взяли межу відповідної суми Рімана. Для скалярних поверхневих інтегралів ми подрібнюємо область області (більше не крива) на крихітні шматочки і продовжуємо таким же чином.
\(S\)Дозволяти бути кусково гладка поверхня з параметризації\(\vecs{r}(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle \) з параметром області\(D\) і нехай\(f(x,y,z)\) бути функція з доменом, який містить\(S\). Наразі припустимо, що домен параметра\(D\) є прямокутником, але ми можемо розширити основну логіку того, як ми перейдемо до будь-якого домену параметрів (вибір прямокутника просто для того, щоб зробити позначення більш керованим). \(D\)Розділіть прямокутник на підпрямокутники\(D_{ij}\) з горизонтальною шириною\(\Delta u\) і вертикальною довжиною\(\Delta v\). Припустимо, що\(i\) коливається від\(1\) до\(m\) і\(j\) коливається від\(1\) до\(n\) так, що\(D\) підрозділяється на\(mn\) прямокутники. Це\(D\) поділ на підпрямокутники дає відповідне\(S\) поділ на шматки\(S_{ij}\). Виберіть точку\(P_{ij}\) в кожному фрагменті,\(S_{ij}\) оцініть\(P_{ij}\) на\(f\), і помножте на площу,\(S_{ij}\) щоб сформувати суму Рімана
\[\sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \, \Delta S_{ij}. \nonumber \]
Щоб визначити поверхневий інтеграл скалярно-значної функції, ми дозволимо областям шматочків\(S\) скорочуватися до нуля, взявши межу.
Поверхневий інтеграл скалярно-значної функції на\(f\) над кусково-гладкою\(S\) поверхнею
\[\iint_S f(x,y,z) dA = \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}. \nonumber \]
Знову ж таки, зверніть увагу на подібність між цим визначенням і визначенням скалярного лінійного інтеграла. При визначенні лінійного інтеграла ми рубаємо криву на шматки, оцінюємо функцію в точці кожного шматка і дозволяємо довжині шматочків зменшитися до нуля, взявши межу відповідної суми Рімана. При визначенні поверхневого інтеграла ми рубаємо поверхню на шматки, оцінюємо функцію в точці кожного шматка і дозволяємо площі шматочків зменшитися до нуля, взявши межу відповідної суми Рімана. Таким чином, поверхневий інтеграл схожий на лінійний інтеграл, але в одному вищому вимірі.
Визначення скалярного лінійного інтеграла можна розширити на області параметрів, які не є прямокутниками, використовуючи ту саму логіку, яка використовувалася раніше. Основна ідея полягає в тому, щоб подрібнити домен параметра на дрібні шматочки, вибрати точку вибірки в кожному шматку і так далі. Точна форма кожного фрагмента в області зразка стає неактуальною, оскільки ділянки частин зменшуються до нуля.
Скалярні поверхневі інтеграли важко обчислити з визначення, як і скалярні лінійні інтеграли. Щоб розробити метод, який полегшує обчислення поверхневих інтегралів, ми наближаємо ділянки поверхні\(\Delta S_{ij}\) невеликими шматочками дотичної площини, як ми це робили в попередньому підрозділі. Нагадаємо визначення векторів\(\vecs t_u\) і\(\vecs t_v\):
\[\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\, \text{and} \, \vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
З матеріалу, який ми вже вивчили, ми знаємо, що
\[\Delta S_{ij} \approx ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})|| \,\Delta u \,\Delta v. \nonumber \]
Тому,
\[\iint_S f(x,y,z) \,dS \approx \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij})|| \vecs t_u(P_{ij}) \times \vecs t_v(P_{ij}) ||\,\Delta u \,\Delta v. \nonumber \]
Це наближення стає довільно близьким до того\(\displaystyle \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}\), як ми збільшуємо кількість штук,\(S_{ij}\) відпускаючи\(m\) і\(n\) йдемо до нескінченності. Тому ми маємо наступне рівняння для обчислення скалярних поверхневих інтегралів:
\[\iint_S f(x,y,z)\,dS = \iint_D f(\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA. \label{scalar surface integrals} \]
Рівняння\ ref {скалярні поверхневі інтеграли} дозволяє обчислити поверхневий інтеграл шляхом перетворення його в подвійний інтеграл. Це рівняння для поверхневих інтегралів аналогічно рівнянню для лінійних інтегралів:
\[\iint_C f(x,y,z)\,ds = \int_a^b f(\vecs r(t))||\vecs r'(t)||\,dt. \nonumber \]
При цьому вектор\(\vecs t_u \times \vecs t_v\) перпендикулярний поверхні, тоді як вектор\(\vecs r'(t)\) - по дотичній до кривої.
Обчислити інтеграл поверхні
\[\iint_S 5 \, dS, \nonumber \]
де\(S\) поверхня з параметризацією\(\vecs r(u,v) = \langle u, \, u^2, \, v \rangle\) для\(0 \leq u \leq 2\) і\(0 \leq v \leq u\).
Рішення
Зверніть увагу, що цей параметр домену\(D\) є трикутником, і тому домен параметра не є прямокутним. Це не є проблемою, оскільки Equation\ ref {скалярні поверхневі інтеграли} не встановлює жодних обмежень на форму області параметрів.
Щоб використати Equation\ ref {скалярні поверхневі інтеграли} для обчислення поверхневого інтеграла, спочатку знайдемо вектори\(\vecs t_u\) і\(\vecs t_v\). Зверніть увагу, що\(\vecs t_u = \langle 1, 2u, 0 \rangle\) і\(\vecs t_v = \langle 0,0,1 \rangle\). Тому,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \nonumber \\ 1 & 2u & 0 \nonumber \\ 0 & 0 & 1 \end{vmatrix} = \langle 2u, \, -1, \, 0 \rangle\ \nonumber \]
і
\[||\vecs t_u \times \vecs t_v|| = \sqrt{1 + 4u^2}. \nonumber \]
За рівнянням\ ref {скалярні поверхневі інтеграли},
\ [\ почати {вирівнювати*}\ iInt_S 5\, dS &= 5\ iInt_D\ sqrt {1 + 4u^2}\, Да\\
&= 5\ int_0^2\ int_0^u\ sqrt {1 + 4u^2}\, dv\, du = 5\ int_0^2 u\ sqrt {1 + 4u^2}\, ду\\
&= 5\ ліворуч [\ dfrac {(1+4u^2) ^ {3/2}} {3}\ праворуч] _0^2\\
&=\ dfrac {5 (17^ {3/2} -1)} {3}\ приблизно 115. 15. \ end {вирівнювати*}\]
Обчислити поверхневий інтеграл\(S\),\[\iint_S (x + y^2) \, dS, \nonumber \] де знаходиться циліндр\(x^2 + y^2 = 4, \, 0 \leq z \leq 3\) (рис.\(\PageIndex{15}\)).
Рішення
Для розрахунку поверхневого інтеграла нам спочатку знадобиться параметризація циліндра. А параметризація - це\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, 0 \leq u \leq 2\pi, \, 0 \leq v \leq 3.\)
Дотичними векторами є\(\vecs t_u = \langle \sin u, \, \cos u, \, 0 \rangle\) і\(\vecs t_v = \langle 0,0,1 \rangle\). Потім,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ -\sin u & \cos u & 0 \\ 0 & 0 & 1 \end{vmatrix} = \langle \cos u, \, \sin u, \, 0 \rangle \nonumber \]
і\(||\vecs t_u \times \vecs t_v || = \sqrt{\cos^2 u + \sin^2 u} = 1\). За рівнянням\ ref {скалярні поверхневі інтеграли},
\ [\ почати {вирівнювати*}\ iInt_s f (x, y, z) dS &=\ iInt_D f (\ векс r (u, v)) ||\ векс t_u\ times\ vecs t_v||\, Да\\
&=\ int_0^3\ int_0^ {2\ pi} (\ cos u +\ sin^2 u)\ du\, дв\\
&=\ int_0^3\ ліворуч [\ sin u +\ dfrac {u} {2} -\ dfrac {\ sin (2u)} {4}\ праворуч] _0^ {2\ pi}\, dv\\
&= \ int_0^3\ пі\, дв = 3\ пі. \ end {вирівнювати*}\]
Обчисліть,\[\iint_S (x^2 - z) \,dS, \nonumber \] де\(S\) знаходиться поверхня з параметризацією\(\vecs r(u,v) = \langle v, \, u^2 + v^2, \, 1 \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3.\)
- Підказка
-
Використовуйте Equation\ ref {скалярні поверхневі інтеграли}.
- Відповідь
-
24
Обчисліть інтеграл поверхні,\[\iint_S f(x,y,z)\,dS, \nonumber \] де\(f(x,y,z) = z^2\) і\(S\) є поверхнею, яка складається з шматка сфери\(x^2 + y^2 + z^2 = 4\), який лежить на площині або над нею,\(z = 1\) і диска, який укладений площиною перетину\(z = 1\) і заданою сферою (рис.\(\PageIndex{16}\)).
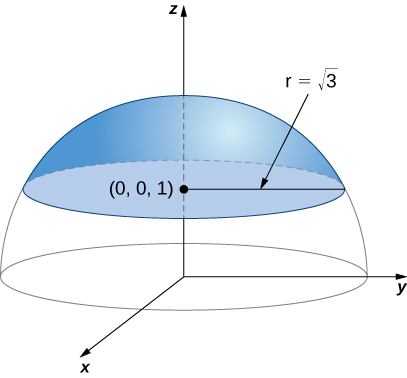
Рішення
Зверніть увагу, що\(S\) це не гладко, але є кусково гладким;\(S\) може бути записано як об'єднання його основи\(S_1\) та сферичної вершини\(S_2\), і обидва\(S_1\) і\(S_2\) гладкі. Тому, щоб розрахувати
\[\iint_S z^2 dS, \nonumber \]
ми пишемо цей інтеграл як
\[\iint_{S_1} z^2 \,dS + \iint_{S_2} z^2 \,dS \nonumber \]
і обчислюємо інтеграли
\[\iint_{S_1} z^2 \,dS \nonumber \]
і
\[\iint_{S_2}Z^2 \,dS. \nonumber \]
Для початку обчислимо\(\displaystyle \iint_{S_1} z^2 \,dS.\) Для обчислення цього інтеграла нам потрібна параметризація\(S_1\). Ця поверхня являє собою диск в площині по\(z = 1\) центру\((0,0,1)\). Щоб параметризувати цей диск, нам потрібно знати його радіус. Оскільки диск утворюється там, де площина\(z = 1\) перетинає сферу\(x^2 + y^2 + z^2 = 4\), ми можемо\(z = 1\) підставити в рівняння\(x^2 + y^2 + z^2 = 4\):
\[x^2 + y^2 + 1 = 4 \Rightarrow x^2 + y^2 = 3. \nonumber \]
Тому радіус диска є\(\sqrt{3}\) і параметризація\(S_1\) є\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, 1 \rangle, \, 0 \leq u \leq \sqrt{3}, \, 0 \leq v \leq 2\pi\). Дотичні вектори є\(\vecs t_u = \langle \cos v, \, \sin v, \, 0 \rangle \) і\(\vecs t_v = \langle -u \, \sin v, \, u \, \cos v, \, 0 \rangle\), і таким чином
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \cos v & \sin v & 0 \\ -u\sin v & u\cos v& 0 \end{vmatrix} = \langle 0, \, 0, u \, \cos^2 v + u \, \sin^2 v \rangle = \langle 0, 0, u \rangle. \nonumber \]
Величина цього вектора дорівнює\(u\). Тому,
\ [\ почати {align*}\ iint_ {S_1} z^2\, dS &=\ int_0^ {\ sqrt {3}}\ int_0^ {2\ pi} f (r (u, v)) ||t_u\ times t_v||\, dv\, du\\
&=\ int_0^ {\ sqrt {3}\ int__0^ {2\ пі} у\, дв\, ду\\
&= 2\ пі\ int_0^ {\ sqrt {3}} u\, ду\\
&= 2\ пі\ sqrt {3}. \ end {вирівнювати*}\]
Тепер обчислюємо
\[\iint_{S_2} \,dS. \nonumber \]
Щоб обчислити цей інтеграл, нам знадобиться параметризація\(S_2\). Параметризація повної сфери\(x^2 + y^2 + z^2 = 4\) є
\[\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, 0 \leq \phi \leq \pi. \nonumber \]
Оскільки ми беремо лише шматок сфери на площині або над\(z = 1\) нею, ми повинні обмежити область\(\phi\). Щоб побачити, наскільки далеко цей кут змітає, зверніть увагу, що кут може розташовуватися в прямокутному трикутнику, як показано на малюнку\(\PageIndex{17}\) (\(\sqrt{3}\)походить від того, що основою\(S\) є диск з радіусом\(\sqrt{3}\)). Тому тангенс\(\phi\) є\(\sqrt{3}\), що має на увазі, що\(\phi\) є\(\pi / 6\). Тепер у нас є параметризація\(S_2\):
\(\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi / 3.\)
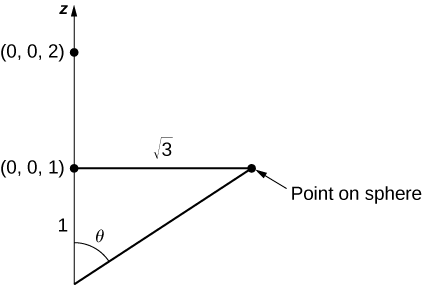
Дотичні вектори є\(\vecs t_{\phi} = \langle 2 \, \cos \theta \, \cos \phi, \, 2 \, \sin \theta \,\cos \phi, \, -2 \, \sin \phi \rangle\) і\(\vecs t_{\theta} = \langle - 2 \sin \theta \sin \phi, \, u\cos \theta \sin \phi, \, 0 \rangle\), і таким чином
\ [\ почати {вирівнювати*}\ vecs t_ {\ phi}\ раз\ vecs t_ {\ тета} &=\ почати {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\ nonномер\\ 2\ cos\ тета\ cos\ cos\ phi & 2\ sin\ тета\ cos\ phi & -2\ sin\ phi\\ -2\ sin\ тета\ sin\ sin\ phi & 2\ cos\ тета\ sin\ phi & 0\ end {vmatrix}\\ [4 pt]
&=\ лангле 4\,\ cos\ тета\,\ sin^2\ фі,\, 4\,\ sin\ тета\,\ sin^2\ фі,\, 4\,\ cos\ theta\,\ cos\ phi\,\ sin\ phi\,\ sin\ phi\ [4 pt]
=\ ланголь 4\,\ cos\ тета\,\ sin^2\ фі,\, 4\,\ sin\ тета\,\ sin^2\ фі,\, 4\,\ cos\ фі\,\ sin\ phi\ rangle. \ end {вирівнювати*}\]
Величина цього вектора дорівнює
\ [\ почати {вирівнювати*}\ векс t_ {\ phi}\ раз\ векс t_ {\ тета} &=\ sqrt {16\,\ cos^2\ тета\,\ sin^4\ phi + 16\,\ sin^2\ theta\,\ sin^4\ phi + 16\,\ cos^2\ phi\,\ sin^2\ phi}\ [pt 4]
&= 4\ sqrt {\ sin^4\ phi +\ cos^2\ phi\,\ sin^2\ phi}. \ end {вирівнювати*}\]
Тому,
\ [\ begin {align*}\ iint_ {S_2} z\, dS &=\ int_0^ {\ pi/6}\ int_0^ {2\ pi} f (\ векс r (\ фі,\ тета)) ||\ векс t_ {\ phi}\ times\ vecs t_ {\ тета} ||, d\ тета\, d\ phi\\
&=\ int_0^ {\ pi/6}\ int_0^ {2\ pi} 16\,\ cos^2\ phi\ sqrt {\ sin^4\ phi +\ cos^2\ phi\,\ sin^2\ phi}\, d\ тета\, d\ фі\\
&= 32\ пі\ int_0^ {\ pi/6}\ cos^2\ фі\ sqrt {\ sin^4\ phi +\ cos^2\ phi\,\ sin^2\ phi}\, d\ phi\\
&= 32\ пі\ int_0^ {\ pi/6}\ cos^2\ phi\,\ sin\ phi\ sqrt {\ sin^2\ phi\\ cos^2\ phi}\, d\ фі\\
&= 32\ пі\ int_0^ {\ pi/6}\ cos^2\ фі\,\ грін\ фі\, д\ фі\\
& = 32\ пі\ ліворуч [-\ dfrac {\ cos^3\ phi} {3}\ праворуч] _0^ {\ pi/6}\
&= 32\ пі\ ліворуч [\ dfrac {1} {3} -\ dfrac {\ sqrt {3}} {8}\ праворуч] =\ dfrac {32\ pi} {3} - 4\ sqrt {3}}. \ end {вирівнювати*}\]
Так як
\[\iint_S z^2 \,dS = \iint_{S_1}z^2 \,dS + \iint_{S_2}z^2 \,dS, \nonumber \]
у нас є
\[\iint_S z^2 \,dS = (2\pi - 4) \sqrt{3} + \dfrac{32\pi}{3}. \nonumber \]
Аналіз
У цьому прикладі ми розбили поверхневий інтеграл над кусковою поверхнею при додаванні поверхневих інтегралів над гладкими підповерхнями. У цьому прикладі було лише дві гладкі підповерхні, але ця техніка поширюється на скінченно багато гладких підповерхонь.
Обчисліть лінійний інтеграл\(x^2 + y^2 = 1, \, 0 \leq z \leq 2\),\(\displaystyle \iint_S (x - y) \, dS,\) де\(S\) знаходиться циліндр, включаючи круглий верх і низ.
- Підказка
-
Розбийте інтеграл на три окремих поверхневих інтеграла.
- Відповідь
-
0
Скалярні поверхневі інтеграли мають кілька реальних застосувань. Нагадаємо, що скалярні лінійні інтеграли можуть бути використані для обчислення маси дроту з урахуванням його функції щільності. Аналогічним чином ми можемо використовувати скалярні поверхневі інтеграли для обчислення маси аркуша, враховуючи його функцію щільності. Якщо тонкий лист металу має форму поверхні,\(S\) а щільність листа в точці\((x,y,z)\) дорівнює,\(\rho(x,y,z)\) то маса\(m\) листа
\[\displaystyle m = \iint_S \rho (x,y,z) \,dS. \label{mass} \]
Плоский лист металу має форму поверхні\(z = 1 + x + 2y\), яка лежить над прямокутником\(0 \leq x \leq 4\) і\(0 \leq y \leq 2\). Якщо щільність листа задана\(\rho (x,y,z) = x^2 yz\), яка маса листа?
Рішення
\(S\)Дозволяти поверхню, яка описує аркуш. Потім маса листа задається\(\displaystyle m = \iint_S x^2 yx \, dS.\) для обчислення цього поверхневого інтеграла, нам спочатку потрібна параметризація\(S\). Оскільки\(S\) задається функцією\(f(x,y) = 1 + x + 2y\), параметризація\(S\) є\(\vecs r(x,y) = \langle x, \, y, \, 1 + x + 2y \rangle, \, 0 \leq x \leq 4, \, 0 \leq y \leq 2\).
Дотичними векторами є\(\vecs t_x = \langle 1,0,1 \rangle\) і\(\vecs t_y = \langle 1,0,2 \rangle\). Тому\(\vecs t_x + \vecs t_y = \langle -1,-2,1 \rangle\) і\(||\vecs t_x \times \vecs t_y|| = \sqrt{6}\).
За визначенням лінійного інтеграла (Розділ 16.2),\ [\ begin {align*} m &=\ iInt_s x^2 yz\, dS\\ [4pt]
&=\ sqrt {6}\ int_0^4\ int_0^2 x^2 y (1 + x + 2y)\, dy\, dx\\ [4pt]
&=\ sqrt {6] &=\ sqrt {6}\ int_0^4\ dfrac {22x^2} {3} + 2x^3\, дх\\ [4pt]
&=\ dfrac {2560\ sqrt { 6}} {9}\ приблизно 696,74. \ end {вирівнювати*}\]
Шматок металу має форму, яка моделюється\(z = x^2 + y^2, \, 0 \leq z \leq 4,\) параболоїдом і щільність металу задається\(\rho (x,y,z) = z + 1\). Знайдіть масу шматка металу.
- Підказка
-
Маса аркуша задається рівнянням\ ref {mass}. Корисна параметризація параболоїду була дана в попередньому прикладі.
- Відповідь
-
\(38.401 \pi \approx 120.640\)
Орієнтація поверхні
Нагадаємо, що коли ми визначили скалярний лінійний інтеграл, нам не потрібно було турбуватися про орієнтацію кривої інтеграції. Те ж саме було і для скалярних поверхневих інтегралів: нам не потрібно було турбуватися про «орієнтацію» поверхні інтеграції.
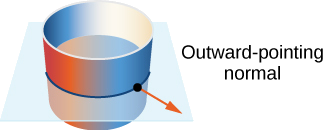
З іншого боку, коли ми визначали векторні лінійні інтеграли, крива інтеграції потребувала орієнтації. Тобто нам знадобилося поняття орієнтованої кривої, щоб визначити векторний інтеграл прямої без двозначності. Аналогічно, коли ми визначаємо поверхневий інтеграл векторного поля, нам потрібно поняття орієнтованої поверхні. Орієнтованій поверхні надається орієнтація «вгору» або «вниз» або, у випадку таких поверхонь, як сфера або циліндр, орієнтація «назовні» або «всередину».
Нехай S буде гладкою поверхнею. Для будь-якої точки\((x,y,z)\) на\(S\), ми можемо визначити два одиничні нормальні вектори\(\vecs N\) і\(-\vecs N\). Якщо є можливість вибрати одиницю нормального вектора\(\vecs N\) в кожній точці\((x,y,z)\) на\(S\) так, що\(\vecs N\) змінюється безперервно\(S\), то\(S\) є «орієнтованим». Такий вибір одиничного вектора нормалі в кожній точці дає орієнтацію поверхні\(S\). Якщо ви думаєте про нормальне поле як про опис потоку води, то сторона поверхні, до якої стікає вода, є «негативною» стороною, а сторона поверхні, на якій стікає вода, є «позитивною» стороною. Неофіційно вибір орієнтації дає «\(S\)зовнішню» сторону і «внутрішню» сторону (або «вгору» і «вниз» сторону), так само як вибір орієнтації кривої дає криві напрямки «вперед» і «назад».
Закриті поверхні, такі як сфери, орієнтовані: якщо ми виберемо зовнішній вектор нормалі в кожній точці на поверхні сфери, то одиничні нормальні вектори безперервно змінюються. Це називається позитивною орієнтацією замкнутої поверхні (рис.\(\PageIndex{18}\)). Ми також могли б вибрати внутрішній нормальний вектор у кожній точці, щоб дати орієнтацію «всередину», яка є негативною орієнтацією поверхні.
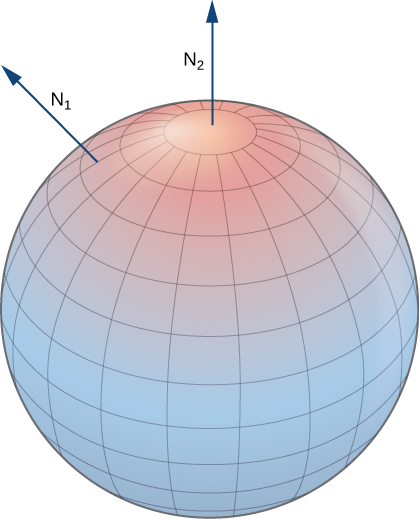
Частина графіка будь-якої гладкої функції\(z = f(x,y)\) також орієнтується. Якщо ми виберемо одиничний нормальний вектор, який вказує «над» поверхнею в кожній точці, то одиничні нормальні вектори безперервно змінюються по поверхні. Ми також могли б вибрати одиничний нормальний вектор, який вказує «нижче» поверхні в кожній точці. Щоб отримати таку орієнтацію, параметризуємо граф стандартним способом:\(\vecs r(x,y) = \langle x,\, y, \, f(x,y)\rangle\), де\(x\) і\(y\) варіюємо по області\(f\).\(f\) Тоді,\(\vecs t_x = \langle 1,0,f_x \rangle\) і\(\vecs t_y = \langle 0,1,f_y \rangle \), отже, перехресний твір\(\vecs t_x \times \vecs t_y\) (який є нормальним до поверхні в будь-якій точці на поверхні) є\(\langle -f_x, \, -f_y, \, 1 \rangle \) Оскільки\(z\) -компонент цього вектора один, відповідний одиничний нормальний вектор вказує «вгору», а висхідна сторона поверхні вибирається на бути «позитивною» стороною.
\(S\)Дозволяти бути гладкою орієнтованої поверхнею з параметризацією\(\vecs r(u,v)\). Для кожної точки\(\vecs r(a,b)\) на поверхні вектори\(\vecs t_u\) і\(\vecs t_v\) лежать в дотичній площині в цій точці. Вектор\(\vecs t_u \times \vecs t_v\) є нормальним до дотичної площини в\(\vecs r(a,b)\) і, отже, є нормальним до\(S\) цієї точки. Тому вибір одиниці нормального вектора
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
дає орієнтацію поверхні\(S\).
Дайте орієнтацію циліндра\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\).
Рішення
Ця поверхня має параметризацію\(\vecs r(u,v) = \langle r \, \cos u, \, r \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h.\)
Дотичними векторами є\(\vecs t_u = \langle -r \, \sin u, \, r \, \cos u, \, 0 \rangle \) і\(\vecs t_v = \langle 0,0,1 \rangle\). Щоб отримати орієнтацію поверхні, обчислюємо одиничний вектор нормалі
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
У цьому випадку\(\vecs t_u \times \vecs t_v = \langle r \, \cos u, \, r \, \sin u, \, 0 \rangle\) і тому
\[||\vecs t_u \times \vecs t_v|| = \sqrt{r^2 \cos^2 u + r^2 \sin^2 u} = r. \nonumber \]
Орієнтація циліндра
\[\vecs N(u,v) = \dfrac{\langle r \, \cos u, \, r \, \sin u, \, 0 \rangle }{r} = \langle \cos u, \, \sin u, \, 0 \rangle. \nonumber \]
Зверніть увагу, що всі вектори паралельні\(xy\) -площині, що має бути у випадку з векторами, які є нормальними до циліндра. Крім того, всі вектори вказують назовні, і тому це зовнішня орієнтація циліндра (рис.\(\PageIndex{19}\)).
Дайте «вгору» орієнтацію графіка\(f(x,y) = xy\).
- Підказка
-
Параметризуйте поверхню і використовуйте той факт, що поверхня є графіком функції.
- Відповідь
-
\[\vecs{N}(x,y) = \left\langle \dfrac{-y}{\sqrt{1+x^2+y^2}}, \, \dfrac{-x}{\sqrt{1+x^2+y^2}}, \, \dfrac{1}{\sqrt{1+x^2+y^2}} \right\rangle \nonumber \]
Оскільки кожна крива має напрямок «вперед» і «назад» (або, в разі замкнутої кривої, напрямок за годинниковою стрілкою і проти годинникової стрілки), то можна дати орієнтацію будь-якій кривій. Отже, можна думати про кожну криву як орієнтовану криву. Однак це не стосується поверхонь. Деякі поверхні не можуть бути орієнтовані; такі поверхні називаються неорієнтованими. По суті, поверхня може бути орієнтована, якщо поверхня має «внутрішню» сторону і «зовнішню» сторону, або «вгору» і «вниз» сторону. Деякі поверхні скручуються таким чином, що немає чітко визначеного поняття «внутрішньої» або «зовнішньої» сторони.
Класичним прикладом неорієнтованої поверхні є смуга Мебіуса. Для створення смуги Мебіуса візьміть прямокутну смужку паперу, дайте аркушу паперу наполовину скручування, а кінці склейте між собою (рис.\(\PageIndex{20}\)). Через напівскручування в смузі поверхня не має «зовнішньої» сторони або «внутрішньої» сторони. Якщо ви уявляєте, що ви розміщуєте нормальний вектор в точці на смузі і маючи вектор рухатися весь шлях навколо смуги, то (через напівскручування) вектор вказує в протилежному напрямку, коли він повертається у вихідне положення. Тому смужка дійсно має тільки одну сторону.

Оскільки деякі поверхні є неорієнтованими, неможливо визначити інтеграл векторної поверхні на всіх кусково-гладких поверхнях. Це на відміну від векторних лінійних інтегралів, які можуть бути визначені на будь-якій кусково-гладкій кривій.
Поверхневий інтеграл векторного поля
Маючи ідею орієнтованих поверхонь на місці, ми тепер готові визначити поверхневий інтеграл векторного поля. Визначення аналогічно визначенню потоку векторного поля вздовж плоської кривої. Нагадаємо, що якщо\(\vecs{F}\) є двовимірним векторним полем і\(C\) являє собою площину кривої, то при визначенні потоку\(\vecs{F}\) вздовж\(C\) беруть участь рубання на дрібні\(C\) шматочки, вибір точки всередині кожного шматка, і обчислення\(\vecs{F} \cdot \vecs{N}\) в точці (де\(\vecs{N}\) знаходиться одиниця нормального вектора в точці). Визначення поверхневого інтеграла векторного поля триває таким же чином, за винятком того, що тепер ми рубаємо поверхню\(S\) на дрібні шматочки, вибираємо точку в малому (двовимірному) шматочку і обчислюємо\(\vecs{F} \cdot \vecs{N}\) в точці.
Щоб помістити це визначення в реальній обстановці, нехай\(S\) бути орієнтованою поверхнею з одиничним нормальним вектором\(\vecs{N}\). \(\vecs{v}\)Дозволяти поле швидкості рідини, що протікає через\(S\), і припустимо, що рідина має щільність\(\rho(x,y,z)\) Уявіть\(S\), що рідина протікає через, але повністю проникна, так що вона не\(S\) перешкоджає потоку рідини (рис.\(\PageIndex{21}\)). Масовий потік рідини - це швидкість масової витрати на одиницю площі. Масовий потік вимірюється в масі в одиницю часу на одиницю площі. Як ми могли обчислити масовий потік рідини поперек\(S\)?
Швидкість потоку, виміряна в масі в одиницю часу на одиницю площі, становить\(\rho \vecs N\). Щоб розрахувати потік маси поперек\(S\), порубати\(S\) на невеликі шматочки\(S_{ij}\). Якщо\(S_{ij}\) досить малий, то він може бути наближений дотичною площиною в якомусь\(P\) точці\(S_{ij}\). Таким чином, одиничний нормальний вектор в\(P\) може бути використаний для наближення\(\vecs N(x,y,z)\) по всій частині,\(S_{ij}\) оскільки нормальний вектор до площини не змінюється, коли ми рухаємося по площині. Складова вектора\(\rho v\) при Р в напрямку\(\vecs{N}\) знаходиться\(\rho \vecs v \cdot \vecs N\) в\(P\). Оскільки\(S_{ij}\) він невеликий, точковий добуток\(\rho v \cdot N\) змінюється дуже мало, оскільки ми варіюємось,\(S_{ij}\) і тому\(\rho \vecs v \cdot \vecs N\) можна сприймати як приблизно постійний поперек\(S_{ij}\). Щоб наблизити масу рідини за одиницю часу, що протікає поперек\(S_{ij}\) (а не тільки локально в точці\(P\)), нам потрібно\((\rho \vecs v \cdot \vecs N) (P)\) помножити на площу\(S_{ij}\). Тому маса рідини за одиницю часу, що протікає\(S_{ij}\) в напрямку,\(\vecs{N}\) може бути наближена\((\rho \vecs v \cdot \vecs N)\Delta S_{ij}\) куди\(\vecs{N}\),\(\rho\) і\(\vecs{v}\) всі оцінюються на\(P\) (рис.\(\PageIndex{22}\)). Це аналогічно потоку двовимірного векторного поля\(\vecs{F}\) по площині кривої\(C\), в якому ми наблизили потік через невеликий шматочок\(C\) з виразом\((\vecs{F} \cdot \vecs{N}) \,\Delta s\). Щоб наблизити потік маси поперек\(S\), сформуйте суму
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
У міру того, як шматочки\(S_{ij}\) стають менше, сума
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij} \nonumber \]
потрапляє довільно близько до потоку маси. Тому потік маси становить
\[\iint_s \rho \vecs v \cdot \vecs N \, dS = \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
Це поверхневий інтеграл векторного поля. Дозволення векторного поля\(\rho \vecs{v}\) довільним векторним полем\(\vecs{F}\) призводить до наступного визначення.
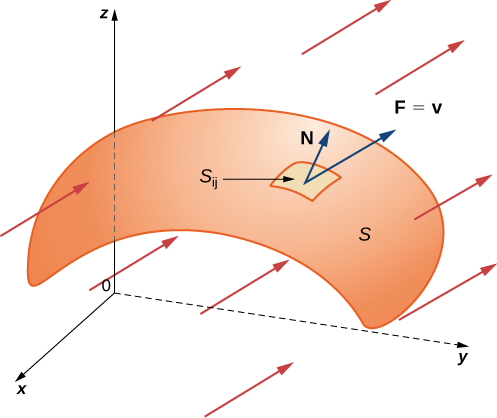
\(\vecs{F}\)Дозволяти безперервне векторне поле з областю, що містить орієнтовану поверхню\(S\) з одиничним нормальним вектором\(\vecs{N}\). Поверхневий інтеграл\(\vecs{F}\) над\(S\) є
\[\iint_S \vecs{F} \cdot \vecs{S} = \iint_S \vecs{F} \cdot \vecs{N} \,dS. \label{surfaceI} \]
Зверніть увагу на паралель між цим визначенням та визначенням векторного лінійного інтеграла\(\displaystyle \int_C \vecs F \cdot \vecs N\, dS\). Поверхневий інтеграл векторного поля визначається аналогічно інтегралу лінії потоку через криву, за винятком того, що областю інтеграції є поверхня (двовимірний об'єкт), а не крива (одновимірний об'єкт). Інтеграл\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) називається потік\(\vecs{F}\) поперек\(S\), так само, як інтеграл\(\displaystyle \int_C \vecs F \cdot \vecs N\,dS\) потік\(\vecs F\) поперечної кривої\(C\). Поверхневий інтеграл над векторним полем також називають інтегралом потоку.
Так само, як і з векторними лінійними інтегралами,\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) поверхневий\(S\) інтеграл легше обчислити після параметризації поверхні. \(\vecs r(u,v)\)Дозволяти параметризація\(S\) з параметром домену\(D\). Потім одиничний вектор нормальної задається\(\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||}\) і, з Equation\ ref {SurfaceI}, ми маємо
\ [\ почати {вирівнювати*}\ int_c\ векс F\ cdot\ векс N\, DS &=\ INT_s\ векс F\ ddot\ dfrac {\ vecs t_u\ раз\ vecs t_v} {||\ vecs t_u\ times\ vecs t_v||}, dS\\ [4pt]
&=\ int_d\ ліворуч (\ векс F (\ векс r (u, v))\ точка\ dfrac {\ векс t_u\ times\ vecs t_v} {||\ векс t_u\ times\ vecs t_v||}\ вправо) |\ векс t_u \ раз\ векс t_v ||\, Да\\ [4пт]
&=\ iInt_D (\ векс F (\ векс r (u, v))\ cdot (\ векс t_u\ times\ vecs t_v))\, Да. \ end {вирівнювати*}\]
Тому для обчислення поверхневого інтеграла над векторним полем ми можемо використовувати рівняння.
\[\iint_S \vecs F \cdot \vecs N\, dS = \iint_D (\vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v)) \,dA. \label{equation 5} \]
Обчисліть поверхневий інтеграл
\[\iint_S \vecs F \cdot \vecs N\,dS, \nonumber \]
де\(\vecs{F} = \langle -y,x,0\rangle\) і\(S\) знаходиться поверхня з параметризацією
\[\vecs r(u,v) = \langle u,v^2 - u, \, u + v\rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 4. \nonumber \]
Рішення
Дотичними векторами є\(\vecs t_u = \langle 1,-1,1\rangle\) і\(\vecs t_v = \langle 0,2v,1\rangle\). Тому,
\[\vecs t_u \times \vecs t_v = \langle -1 -2v, -1, 2v\rangle. \nonumber \]
За рівнянням\ ref {рівняння 5},
\[ \begin{align*} \iint_S \vecs F \cdot dS &= \int_0^4 \int_0^3 F (\vecs r(u,v)) \cdot (\vecs t_u \times \vecs t_v) \, du \,dv \\[4pt] &= \int_0^4 \int_0^3 \langle u - v^2, \, u, \, 0\rangle \cdot \langle -1 -2v, \, -1, \, 2v\rangle \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 [(u - v^2)(-1-2v) - u] \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 (2v^3 + v^2 - 2uv - 2u) \, du\,dv \\[4pt] &= \int_0^4 \left.[2v^3u + v^2u - vu^2 - u^2]\right|_0^3 \, dv \\[4pt] &= \int_0^4 (6v^3 + 3v^2 - 9v - 9) \, dv \\[4pt] &= \left[ \dfrac{3v^4}{2} + v^3 - \dfrac{9v^2}{2} - 9v\right]_0^4\\[4pt] &= 340. \end{align*}\]
Тому потік\(\vecs{F}\) поперек\(S\) дорівнює 340.
Обчисліть поверхневий інтеграл,\[\iint_S \vecs F \cdot \vecs N \, dS, \nonumber \] де\(\vecs F = \langle 0, -z, y \rangle\) і\(S\) є частиною одиничної сфери в першому октанті з зовнішньою орієнтацією.
- Підказка
-
Використовуйте рівняння\ ref {рівняння 5}.
- Відповідь
-
0
Нехай\(\vecs v(x,y,z) = \langle 2x, \, 2y, \, z\rangle\) являють собою поле швидкості (з одиницями метрів в секунду) рідини з постійною щільністю 80 кг/м 3. \(S\)Дозволяти бути півсфера\(x^2 + y^2 + z^2 = 9\) з\(z \leq 0\) такою, що\(S\) орієнтована назовні. Знайдіть масову витрату рідини поперек\(S\).
Рішення
А параметризація поверхні - це
\[\vecs r(\phi, \theta) = \langle 3 \, \cos \theta \, \sin \phi, \, 3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi/2. \nonumber \]
Як і в прикладі, дотичні вектори є\(\vecs t_{\theta} = \langle -3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \theta \, \sin \phi, \, 0 \rangle \)\( \vecs t_{\phi} = \langle 3 \, \cos \theta \, \cos \phi, \, 3 \, \sin \theta \, \cos \phi, \, -3 \, \sin \phi \rangle,\) і їх перехресний добуток
\[\vecs t_{\phi} \times \vecs t_{\theta} = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle. \nonumber \]
Зверніть увагу, що кожна складова перехресного добутку позитивна, і тому цей вектор дає зовнішню орієнтацію. Тому використовуємо орієнтацію
\(\vecs N = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle \)
для сфери.
За\ міткою {SurfaceI},
\ [\ почати {align*}\ iInt_s\ rho v\ cdot\, dS &= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} v (r (\ фі,\ тета))\ cdot (t_ {\ phi}\ times t_ {\ тета})\, d\ phi\, d\ тета\\
&= 80 int_0^ {2\ pi}\ int_0^ {\ pi/2}\ ланголь 6\,\ cos\ тета\,\ sin\ phi,\, 6\,\ sin\ тета\,\ sin\ phi,\, 3\,\ cos\ phi\ rangle\ cdot\ ланголь 9\,\ cos\ тета\,\ sin^2\ фі,\, 9\,\ sin\ тета\,\ sin^2\ фі,\, 9\,\ sin\ фі\,\ cos\ phi\ rangle\, d\ theta\\\
&= 80\ int_0^ {2\ pi}\ int_0^ {int_0^ {int_0^ {int_0^ {\ int_0^ {\ int_0^ {\ int_0^ {\ pi/2},\ sin^3\ phi + 27\,\ cos^2\ phi\,\ sin\ phi\, d\ phi\, d\ тета\\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} 54 (1 -\ cos^2\ phi)\,\ sin\ phi + 27\ cos^2\ phi\,\ sin\ фі\, d\ тета\\\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} 54\,\ sin\ phi - 27\,\ cos^2\ phi\\ грін\ фі\, д\ фі\, д\ тета\\
&= 80\ int_0^ {2\ пі}\ великий [-54\,\ cos\ phi + 9\,\ cos^3\ phi\ Big] _ {\ phi =0} ^ {\ phi=2\ пі}\, d\ тета\\
&=80\ int_0^ {2\ пі} 45\, d\ тета\\
&= 7200\ пі. \ end {вирівнювати*}\ nonumber\]
Тому масова витрата є\(7200\pi \, \text{kg/sec/m}^2\).
Нехай\(\vecs v(x,y,z) = \langle x^2 + y^2, \, z, \, 4y \rangle\) м/с представляють поле швидкості рідини з постійною щільністю 100 кг/м 3. \(S\)Дозволяти бути напівциліндр,\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u \leq \pi, \, 0 \leq v \leq 2\) орієнтований назовні. Розрахуйте масовий потік рідини поперек\(S\).
- Підказка
-
Використовуйте\ label {SurfaceI}.
- Відповідь
-
400 кг/сек/м
У прикладі\(\PageIndex{14}\) ми розрахували масовий потік, який являє собою швидкість масової витрати на одиницю площі. Якщо ми хочемо знайти швидкість потоку (вимірюється в обсязі за час) замість цього, ми можемо використовувати інтеграл потоку
\[\iint_S \vecs v \cdot \vecs N \, dS, \nonumber \]
що залишає густоту. Оскільки витрата рідини вимірюється в обсязі за одиницю часу, витрата маси не враховується. Тому ми маємо наступну характеристику швидкості потоку рідини зі швидкістю\(\vecs v\) по поверхні\(S\):
\[\text{Flow rate of fluid across S} = \iint_S \vecs v \cdot dS. \nonumber \]
Щоб обчислити витрату рідини в прикладі, ми просто видаляємо постійну щільності, яка дає швидкість потоку\(90 \pi \, m^3/sec\).
І масовий потік, і витрата важливі у фізиці та техніці. Масовий потік вимірює, скільки маси протікає по поверхні; швидкість потоку вимірює, скільки обсягу рідини протікає по поверхні.
Крім моделювання потоку рідини, поверхневі інтеграли можуть бути використані для моделювання теплового потоку. Припустимо, що температура\((x,y,z)\) в точці об'єкта є\(T(x,y,z)\). Тоді тепловий потік являє собою векторне поле, пропорційне негативному градієнту температури в об'єкті. Якщо бути точним, то тепловий потік визначається як векторне поле\(F = - k \nabla T\), де постійна k - теплопровідність речовини, з якого зроблений об'єкт (ця константа визначається експериментальним шляхом). Швидкість теплового потоку по поверхні S в об'єкті задається інтегралом потоку
\[\iint_S \vecs F \cdot dS = \iint_S -k \vecs \nabla T \cdot dS. \nonumber \]
Чавунному суцільному циліндру надають нерівності\(x^2 + y^2 \leq 1, \, 1 \leq z \leq 4\). Температура в точці\((x,y,z)\) в області, що містить циліндр, є\(T(x,y,z) = (x^2 + y^2)z\). З огляду на, що теплопровідність чавуну дорівнює 55, знайдіть тепловий потік через межу твердого тіла, якщо ця межа орієнтована назовні.
Рішення
Нехай\(S\) позначають межу об'єкта. Щоб знайти тепловий потік, нам потрібно обчислити інтеграл потоку\[\iint_S -k\vecs \nabla T \cdot dS. \nonumber \] Зверніть увагу, що не\(S\) є гладкою поверхнею, а є кусково-гладкою, оскільки\(S\) є об'єднанням трьох гладких поверхонь (кругової верхньої і нижньої, і циліндричної сторони). Тому обчислюємо три окремих інтеграла, по одному на кожен гладкий шматок\(S\). Перш ніж обчислювати будь-які інтеграли, зверніть увагу, що градієнт температури дорівнює\(\vecs \nabla T = \langle 2xz, \, 2yz, \, x^2 + y^2 \rangle\).
Спочатку розглянемо кругле дно предмета, яке позначимо\(S_1\). Ми бачимо, що\(S_1\) це коло радіуса 1 по центру в точці,\((0,0,1)\) сидячи в площині\(z = 1\). Ця поверхня має параметризацію\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 1 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Тому,
\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\)і\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle\), і\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0, \, 0, -v \rangle\).
Оскільки поверхня орієнтована назовні і\(S_1\) є дном предмета, має сенс, що цей вектор вказує вниз. За рівнянням тепловий потік поперек\(S_1\) дорівнює
\[ \begin{align*}\iint_{S_1} -k \vecs \nabla T \cdot dS &= - 55 \int_0^{2\pi} \int_0^1 \vecs \nabla T(u,v) \cdot (\vecs t_u \times \vecs t_v) \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2 \cos^2 u + v^2 \sin^2 u \rangle \cdot \langle 0,0, -v\rangle \, dv \,du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2\rangle \cdot \langle 0, 0, -v \rangle \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 -v^3 \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} -\dfrac{1}{4} du \\[4pt] &= \dfrac{55\pi}{2}.\end{align*}\]
Тепер розглянемо кругову вершину предмета, яку ми позначимо\(S_2\). Ми бачимо, що\(S_2\) це коло радіусом 1 по центру в точці\((0,0,4)\), сидячи в площині\(z = 4\). Ця поверхня має параметризацію\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 4 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Тому\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\) і\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle \), і\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0,0,-v\rangle\).
Оскільки поверхня орієнтована назовні і\(S_1\) є вершиною об'єкта, ми замість цього беремо вектор\(\vecs t_v \times \vecs t_u = \langle 0,0,v\rangle\). За рівнянням тепловий потік поперек\(S_1\) дорівнює
\ [\ почати {align*}\ iint_ {S_2} -k\ векс\ набла T\ cdot dS &= - 55\ int_0^ {2\ pi}\ int_0^1\ vecs\ nabla T (u, v)\ cdot\, (\ vecs t_u\ times\ vecs t_v)\, dv\, du\\ 4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1\ langle 8v\,\ cos u,\, 8v\,\ sin u,\, v^2\ cos^2 u + v^2\ sin^2 u\ діапазон\ cdot\ langle 0,0, -v\ діапазон\, дв\, ду\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1\ langle 8v\,\ cos u,\, 8v\,\ sin u,\, v^2\ діапазон\ cdot\ langle 0, 0, -v\ діапазон\,\, dv\, du\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1 -v^3\, dv\, du = - 55\ int_0^ {2\ пі} -\ dfrac {1} {4}\, ду = -\ dfrac {55\ пі} {2}. \ end {вирівнювати*}\]
В останню чергу розглянемо циліндричну сторону предмета. Ця поверхня має параметризацію\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 1 \leq v \leq 4\). За прикладом, ми це знаємо\(\vecs t_u \times \vecs t_v = \langle \cos u, \, \sin u, \, 0 \rangle\). За рівнянням
\ [\ почати {align*}\ iint_ {S_3} -k\ векс\ набла T\ cdot dS &= - 55\ int_0^ {2\ pi}\ int_1^4\ vecs\ nabla T (u, v)\ cdot (\ vecs t_u\ times\ vecs t_v)\ dv\, du\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_1^4\ ланголь 2v\,\ cos u,\, 2v\,\ sin u,\,\ cos^2 u\ sin^2 u\ діапазон\ cdot\ лангл\ cos u,\,\ sin u,\, 0\ діапазон\, dv\, ду\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1\ langle 2v\,\ cos^2 u,\, 2v\,\ sin u,\, 1\ діапазон\ cdot\ langle\ cos u,\,\ sin u,\, 0\ rangle\, дв\, ду\\ [4пт]
&= - 55\ int_0^ {2\ пі}\ int_0^1 (2v\,\ cos^2 u + 2v\,\ sin^2 u)\, дв\, ду\\ [4пт]
&= - 55\ int_0^ {2\ пі}\ int_0^1 2v\, дв\, ду\\ [4pt]
&= -55\ int_0^ {2\ пі} ду\\ [4пт]
&= -110\ пі. \ end {вирівнювати*}\]
Тому швидкість теплового потоку поперек\(S\) становить
\[\dfrac{55\pi}{2} - \dfrac{55\pi}{2} - 110\pi = -110\pi. \nonumber \]
Чавунний суцільний куля задається нерівністю\(x^2 + y^2 + z^2 \leq 1\). Температура в точці в області, що містить кулю, є\(T(x,y,z) = \dfrac{1}{3}(x^2 + y^2 + z^2)\). Знайдіть тепловий потік через межу твердого тіла, якщо ця межа орієнтована назовні.
- Підказка
-
Дотримуйтесь інструкцій Приклад\(\PageIndex{15}\).
- Відповідь
-
\(-\dfrac{440\pi}{3}\)
Ключові поняття
- Поверхні можна параметризувати, так само, як криві можна параметризувати. Загалом, поверхні повинні бути параметризовані двома параметрами.
- Поверхні іноді можуть бути орієнтовані, так само, як можна орієнтувати криві. Деякі поверхні, такі як смуга Мебіуса, не можуть бути орієнтовані.
- Поверхневий інтеграл - це як лінійний інтеграл в одному вищому вимірі. Область інтегрування поверхневого інтеграла - це поверхня в площині або просторі, а не крива в площині або просторі.
- Цілим числом поверхневого інтеграла може бути скалярна функція або векторне поле. Щоб обчислити поверхневий інтеграл з цілим числом, який є функцією, використовуйте Рівняння. Для обчислення поверхневого інтеграла з цілим числом, що є векторним полем, використовуйте Рівняння.
- Якщо\(S\) це поверхня, то площа\(S\) становить\[\iint_S \, dS. \nonumber \]
Ключові рівняння
- S рівний інтеграл поверхні
\[\iint_S f(x,y,z) \,dS = \iint_D f (\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA \nonumber \]
- Інтегральний потік
\[\iint_S \vecs F \cdot \vecs N \, dS = \iint_S \vecs F \cdot dS = \iint_D \vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v) \, dA \nonumber \]
Глосарій
- інтегральний потік
- інша назва поверхневого інтеграла векторного поля; бажаний термін у фізиці та техніці
- криві сітки
- криві на поверхні, паралельні лініям сітки в координатній площині
- тепловий потік
- векторне поле, пропорційне негативному градієнту температури в об'єкті
- потік маси
- швидкість масової витрати рідини на одиницю площі, вимірюється в масі в одиницю часу на одиницю площі
- орієнтація поверхні
- якщо поверхня має «внутрішню» сторону і «зовнішню» сторону, то орієнтація - це вибір внутрішньої або зовнішньої сторони; поверхня також може мати «вгору» і «вниз» орієнтації
- параметр домен (простір параметрів)
- область\(uv\) -площини, над якою\(v\) змінюються параметри\(u\) і для параметризації\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\)
- параметризована поверхня (параметрична поверхня)
- поверхню, задана описом форми\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\), де параметри\(v\) змінюються\(u\) і по області параметра в\(uv\) -площині
- регулярна параметризація
- параметризація\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\) така, що не\(r_u \times r_v\) дорівнює нулю для точки\((u,v)\) в області параметра
- площа поверхні
- площа поверхні,\(S\) задана поверхневим інтегралом\[\iint_S \,dS \nonumber \]
- поверхневий інтеграл
- інтеграл функції над поверхнею
- поверхневий інтеграл скалярно-значної функції
- поверхневий інтеграл, в якому integrand є скалярною функцією
- поверхневий інтеграл векторного поля
- поверхневий інтеграл, в якому integrand є векторним полем

З Прикладу випливає\(\PageIndex{1}\), що ми можемо параметризувати всі циліндри форми\(x^2 + y^2 = R^2\). Якщо S - циліндр\(x^2 + y^2 = R^2\), заданий рівнянням, то параметризація\(S\) є\(\vecs r(u,v) = \langle R \, \cos u, \, R \, \sin u, \, v \rangle, \, 0 \leq u \leq 2 \pi, \, -\infty < v < \infty.\)
Ми також можемо знайти різні типи поверхонь, враховуючи їх параметризацію, або ми можемо знайти параметризацію, коли нам дають поверхню.
Приклад\(\PageIndex{2}\): Describing a Surface
Опишіть поверхню,\(S\) параметризовану\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u^2 \rangle, \, 0 \leq u < \infty, \, 0 \leq v < 2\pi\).
Рішення
Зверніть увагу, що якщо\(u\) утримується постійною, то отримана крива є окружністю радіуса\(u\) в площині\(z = u\). Тому зі\(u\) збільшенням радіус отриманої окружності збільшується. Якщо\(v\) утримується постійною, то отримана крива являє собою вертикальну параболу. Тому ми очікуємо, що поверхня буде еліптичним параболоїдом. Щоб підтвердити це, зверніть увагу, що
\[\begin{align*} x^2 + y^2 &= (u \, \cos v)^2 + (u \, \sin v)^2 \\[4pt] &= u^2 \cos^2 v + u^2 sin^2 v \\[4pt] &= u^2 \\[4pt] &=z\end{align*}\]
Тому поверхня являє собою еліптичний параболоїд\(x^2 + y^2 = z\) (рис.\(\PageIndex{3}\)).
Вправа\(\PageIndex{2}\)
Опишіть поверхню, параметризовану\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, - \infty < u < \infty, \, 0 \leq v < 2\pi\).
Тримайте\(u\) постійну і подивіться, які криві вийдуть. Уявіть, що відбувається у міру\(u\) збільшення або зменшення.
Конус\(x^2 + y^2 = z^2\)