7.8: Глава 7 Огляд вправ

Last updated
Save as PDF

Page ID: 62159

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У вправах 1 - 4 визначте, чи є твердження істинним або хибним. Обгрунтуйте свою відповідь доказом або контрприкладом.

1)$\displaystyle ∫e^x\sin(x)\,dx$ не може бути інтегрований частинами.

2)$\displaystyle ∫\frac{1}{x^4+1}\,dx$ не може бути інтегрований з використанням часткових дробів.

Відповідь: Помилковий

3) При числовому інтегруванні збільшення кількості точок зменшує похибку.

4) Інтеграція частинами завжди може дати інтеграл.

Відповідь: Помилковий

У вправах 5 - 10 оцінюйте інтеграл за допомогою зазначеного методу.

5)$\displaystyle ∫x^2\sin(4x)\,dx,$ за допомогою інтеграції частинами

6)$\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx,$ за допомогою тригонометричної заміни

Відповідь: $\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx = −\frac{\sqrt{x^2+16}}{16x}+C$

7)$\displaystyle ∫\sqrt{x}\ln x\,dx,$ за допомогою інтеграції частинами

8)$\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx,$ використання часткових дробів

Відповідь: $\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx = \frac{1}{10}\big(4\ln|2−x|+5\ln|x+1|−9\ln|x+3|\big)+C$

9)$\displaystyle ∫\frac{x^5}{(4x^2+4)^{5/2}}\,dx,$ за допомогою тригонометричного заміщення

10)$\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx,$ за допомогою таблиці інтегралів або CAS

Відповідь: $\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx = −\frac{\sqrt{4−\sin^2(x)}}{\sin(x)}−\frac{x}{2}+C$

У вправах 11 - 15 інтегруйте, використовуючи будь-який метод, який ви виберете.

11)$\displaystyle ∫\sin^2 x\cos^2 x\,dx$

12)$\displaystyle ∫x^3\sqrt{x^2+2}\,dx$

Відповідь: $\displaystyle ∫x^3\sqrt{x^2+2}\,dx = \frac{1}{15}(x^2+2)^{3/2}(3x^2−4)+C$

13)$\displaystyle ∫\frac{3x^2+1}{x^4−2x^3−x^2+2x}\,dx$

14)$\displaystyle ∫\frac{1}{x^4+4}\,dx$

Відповідь: $\displaystyle ∫\frac{1}{x^4+4}\,dx = \frac{1}{16}\ln(\frac{x^2+2x+2}{x^2−2x+2})−\frac{1}{8}\tan^{−1}(1−x)+\frac{1}{8}\tan^{−1}(x+1)+C$

15)$\displaystyle ∫\frac{\sqrt{3+16x^4}}{x^4}\,dx$

У вправах 16 - 18 наближайте інтеграли, використовуючи правило середньої точки, трапецієподібне правило та правило Сімпсона за допомогою чотирьох підінтервалів, округлення до трьох десяткових знаків.

16) [Т]$\displaystyle ∫^2_1\sqrt{x^5+2}\,dx$

Відповідь: $M_4=3.312,$
$T_4=3.354,$
$S_4=3.326$

17) [Т]$\displaystyle ∫^{\sqrt{π}}_0e^{−\sin(x^2)}\,dx$

18) [Т]$\displaystyle ∫^4_1\frac{\ln(1/x)}{x}\,dx$

Відповідь: $M_4=−0.982,$
$T_4=−0.917,$
$S_4=−0.952$

У вправах 19 - 20 оцінюйте інтеграли, якщо це можливо.

19)$\displaystyle ∫^∞_1\frac{1}{x^n}\,dx,$ за якими значеннями$n$ цей інтеграл сходиться або розходиться?

20)$\displaystyle ∫^∞_1\frac{e^{−x}}{x}\,dx$

Відповідь: приблизно 0,2194

У вправах 21 - 22 розглянемо гамма-функцію, задану$\displaystyle Γ(a)=∫^∞_0e^{−y}y^{a−1}\,dy.$

21) Покажіть, що$\displaystyle Γ(a)=(a−1)Γ(a−1).$

22) Розширити, щоб показати, що$\displaystyle Γ(a)=(a−1)!,$ припущення$a$ є додатним цілим числом.

Найшвидший автомобіль у світі, Bugati Veyron, може розвивати максимальну швидкість 408 км/год.

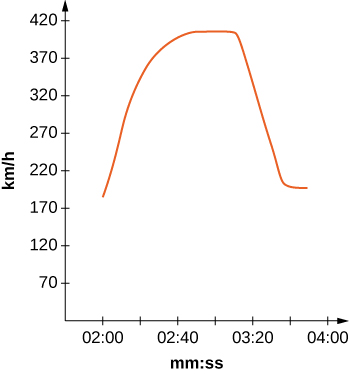
$Ця цифра має графік в першому квадранті. Він збільшується до тих місць, де х приблизно 03:00 мм: сс, а потім опускається крутий. Максимальна висота графіка, тут падіння відбувається приблизно 420 км/ч.$

23) [T] Використовуйте графік, щоб оцінити швидкість кожні 20 сек і відповідати графіку форми$v(t)=ae^{bx}\sin(cx)+d.$ (Підказка: Розглянемо одиниці часу.)

24) [T] Використовуючи свою функцію з попередньої задачі, знайдіть, як саме далеко пройшов Bugati Veyron за 1 хв 40 сек, включених в графік.

Відповідь: Відповіді можуть відрізнятися. Наприклад:$9.405$ км