2.1: Попередній перегляд обчислення

Last updated
Save as PDF

Page ID: 62325

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Опишіть дотичну задачу і як вона привела до ідеї похідної.
Поясніть, як ідея межі бере участь у вирішенні дотичної задачі.
Розпізнати дотичну до кривої в точці як межу січних ліній.
Визначте миттєву швидкість як межу середньої швидкості протягом невеликого часового інтервалу.
Опишіть задачу області та те, як вона була вирішена інтегралом.
Поясніть, як ідея обмеження бере участь у вирішенні проблеми області.
Визнайте, як ідеї граничної, похідної та інтегральної призвели до вивчення нескінченних рядів та багатовимірних числення.

Коли ми приступимо до вивчення обчислення, ми побачимо, як його розвиток виник із загальних рішень практичних проблем у таких сферах, як інженерна фізика, наприклад, проблема космічних подорожей, поставлена в відкритті глави. Дві ключові проблеми призвели до початкового формулювання числення: (1) дотична задача, або як визначити нахил прямої дотичної до кривої в точці; і (2) проблема площі, або як визначити площу під кривою.

Дотична задача та диференціальне числення

Швидкість змін - одне з найбільш критичних понять у обчисленні. Ми починаємо наше дослідження швидкостей зміни з розгляду графіків трьох ліній\(f(x)=−2x−3,\; g(x)=\dfrac{1}{2}x+1\), причому\(h(x)=2\), показаних на малюнку\(\PageIndex{1}\).

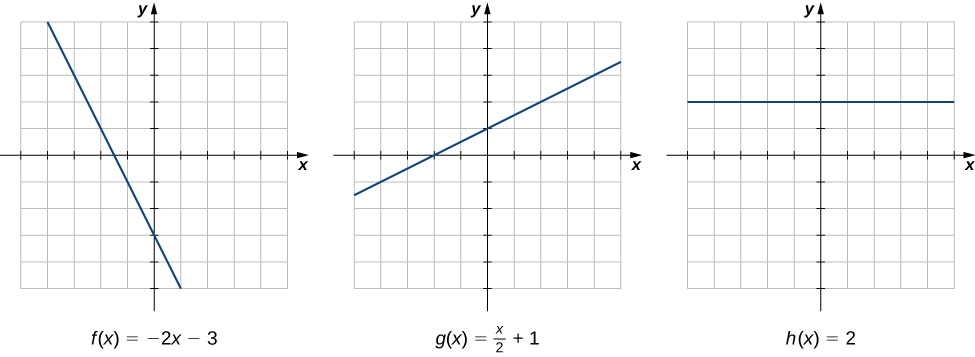
Три прямолінійних графіка. Один, позначений «f (x) = -2x - 3», зменшується, перетинаючи вісь x на -1,5, а вісь y - -3; інший, позначений «g (x) = x/2 + 1,» збільшується, перетинаючи вісь x на -2 і вісь y в 1; третій, позначений «h (x) = 2,» плоский у координаті y 2 — Малюнок\(\PageIndex{1}\): Швидкість зміни лінійної функції є постійною в кожному з цих трьох графіків, причому константа визначається нахилом.

Коли ми рухаємося зліва направо вздовж графіка\(f(x)=−2x−3\), ми бачимо, що графік зменшується з постійною швидкістю. Для кожної\(1\) одиниці ми рухаємося вправо вздовж\(x\) -осі,\(y\) -координата зменшується на\(2\) одиниці. Ця швидкість зміни визначається нахилом (\(−2\)) лінії. Аналогічно, нахил\(1/2\) у функції\(g(x)\) говорить нам, що для кожної\(x\) зміни\(1\) одиниці існує відповідна зміна\(y\)\(1/2\) одиниці. Функція\(h(x)=2\) має нахил нуля, що вказує на те, що значення функції залишаються постійними. Ми бачимо, що нахил кожної лінійної функції вказує на швидкість зміни функції.

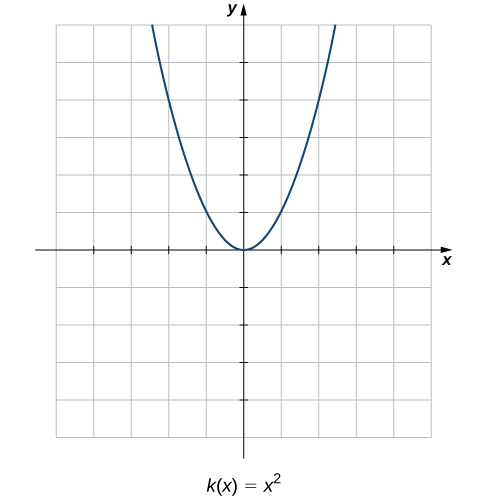
Порівняйте графіки цих трьох функцій з графіком\(k(x)=x^2\) (рис.\(\PageIndex{2}\)). Графік\(k(x)=x^2\) починається зліва, швидко зменшуючись, потім починає зменшуватися повільніше і вирівнюватися, а потім, нарешті, починає збільшуватися - спочатку повільно, а потім збільшується швидкість збільшення, коли вона рухається вправо. На відміну від лінійної функції, жодне єдине число не представляє швидкість зміни для цієї функції. Ми цілком закономірно запитуємо: Як ми вимірюємо швидкість зміни нелінійної функції?

Графік параболи k (x) = x^2, який відкривається і має свою вершину біля початку. — Малюнок\(\PageIndex{2}\): Функція\(k(x)=x^2\) не має постійної швидкості зміни.

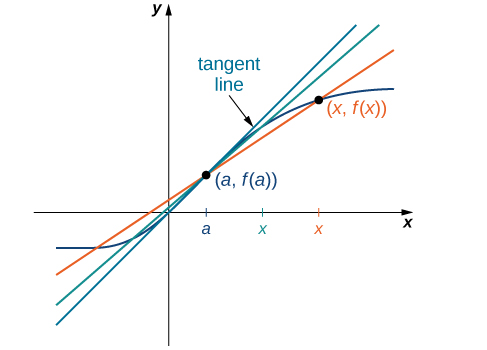
Ми можемо наблизити швидкість зміни функції\(f(x)\) в точці\((a,f(a))\) на її графіку, взявши іншу точку\((x,f(x))\) на графіку\(f(x)\), провівши лінію через дві точки і обчисливши нахил отриманої прямої. Така лінія називається січної лінією. \(\PageIndex{3}\)На малюнку показана січна лінія до функції\(f(x)\) в точці\((a,f(a))\).

Графік, що показує загальну криву функцію, що проходить через точки (0,0), (a, фа.) та (x, f (x)). Пряма лінія, яка називається січною лінією, проводиться через точки (a, фа.), і (x, f (x)), що йде нижче вигнутої функції між a і x і йде над вигнутою функцією при значеннях, більших за x або менше a. вигнута функція і січна лінія перетинаються ще раз в деякій точці третього квадранта. Нахил січної лінії дорівнює (f (x) — фа.)/(x — a). — Малюнок\(\PageIndex{3}\): Нахил січної лінії через точку\((a,f(a))\) оцінює швидкість зміни функції в точці\((a,f(a))\).

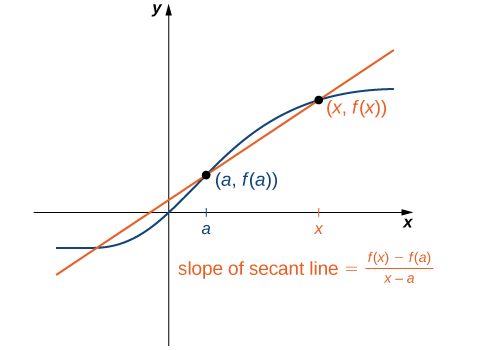
Формально визначаємо січну лінію наступним чином:

Визначення: Січна лінія

Секанс до функції\(f(x)\) через точки\((a,f(a))\) і\((x,f(x))\) є лінією, що проходить через ці точки. Її ухил задається

\[m_{sec}=\dfrac{f(x)−f(a)}{x−a}. \label{secantslope} \]

Точність наближення швидкості зміни функції січною лінією залежить від того, наскільки\(x\) близька до\(a\). Як ми бачимо на малюнку\(\PageIndex{4}\), якщо\(x\) ближче до\(a\), нахил січної лінії є кращою мірою швидкості зміни\(f(x)\) at\(a\).

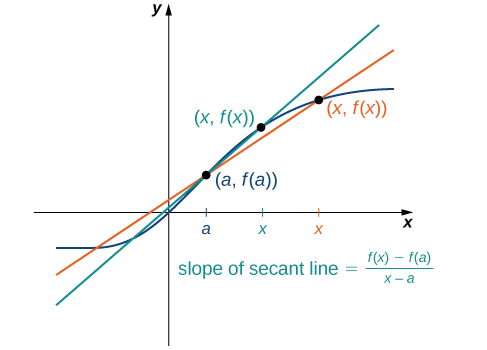
Цей графік збігається з попередньою січною лінією та загальним графіком вигнутих функцій. Однак додається ще одна точка x, на цей раз нанесена ближче до a на осі x. Таким чином, інша січна лінія проводиться через точки (a, фа.) і нову, ближче (x, f (x)). Лінія залишається набагато ближче до загальної вигнутої функції навколо (a, fa.). Нахил цієї січної лінії став кращим наближенням швидкості зміни родової функції. — Малюнок\(\PageIndex{4}\): Коли\(x\) наближається\(a\), нахил січної лінії стає кращим наближенням до швидкості зміни функції\(f(x)\) на\(a\).

Самі січні лінії наближаються до лінії, яка називається дотичною до функції\(f(x)\) at\(a\) (рис.\(\PageIndex{5}\)). Нахил дотичної лінії до графіка при\(a\) вимірює швидкість зміни функції на\(a\). Це значення також представляє похідну функції\(f(x)\) at\(a\), або швидкість зміни функції at\(a\). Ця похідна позначається символом\(f′(a)\). Диференціальне числення - це область числення, що займається вивченням похідних та їх застосувань.

Цей графік є продовженням двох попередніх. Цього разу графік містить вигнуту функцію, дві січні лінії та дотичну лінію. Коли х наближається до a, січні лінії наближаються до дотичної лінії. — Малюнок\(\PageIndex{5}\): Розв'язування дотичної задачі: У міру\(x\)\(a\) наближення січні лінії наближаються до дотичної лінії.

Приклад\(\PageIndex{1}\) ілюструє, як знайти ухили січних ліній. Ці укоси оцінюють ухил дотичної лінії або, що еквівалентно, швидкість зміни функції в точці, в якій розраховуються ухили.

Приклад\(\PageIndex{1}\): Finding Slopes of Secant Lines

Оцінити нахил дотичної лінії (швидкість зміни) до\(f(x)=x^2\) ат\(x=1\) шляхом знаходження нахилів січних ліній через\((1,1)\) і кожну з наступних точок на графіку\(f(x)=x^2\).

\((2,4)\)
\(\left(\dfrac{3}{2},\dfrac{9}{4}\right)\)

Рішення:

Скористайтеся формулою нахилу січної прямої (Equation\ ref {secantslope}).

\(m_{sec}=\dfrac{4−1}{2−1}=3\)
\(m_{sec}=\dfrac{\dfrac{9}{4}−1}{\dfrac{3}{2}−1}=\dfrac{5}{2}=2.5\)

Точка в частині б. ближче до точки\((1,1)\), тому нахил\(2.5\) знаходиться ближче до нахилу дотичної лінії. Хороша оцінка для нахилу дотичної буде в діапазоні\(2\) до\(2.5\) (рис.\(\PageIndex{6}\)).

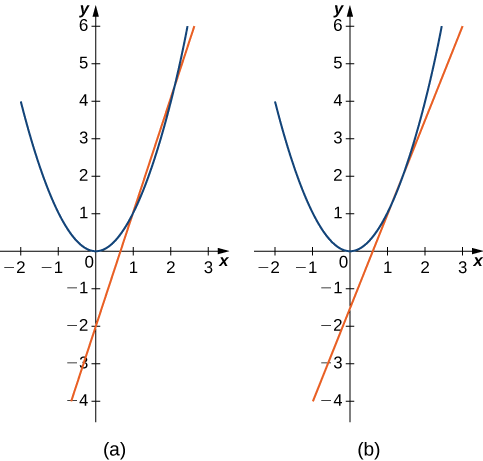
Наведено два графіки параболи f (x) = x^2. Перший має проведену січну лінію, що перетинає параболу в (1,1) і (2,4). Друга має проведену січну лінію, що перетинає параболу в (1,1) і (3/2, 9/4). Ці рядки забезпечують послідовно ближчі наближення до дотичної лінії до функції at (1,1). — Рисунок\(\PageIndex{6}\): Січні лінії до\(f(x)=x^2\) at\((1,1)\) через (a)\((2,4)\) та (b)\((\dfrac{3}{2},\dfrac{9}{4})\) забезпечують послідовно ближчі наближення до дотичної лінії до\(f(x)=x^2\) at\((1,1)\).

Вправа\(\PageIndex{1}\)

Оцінити нахил дотичної лінії (швидкість зміни) до\(f(x)=x^2\) ат\(x=1\) шляхом знаходження нахилів січних ліній наскрізь\((1,1)\) і точки\((\dfrac{5}{4},\dfrac{25}{16})\) на графіку\(f(x)=x^2\).

Відповідь: \(2.25\)

Продовжуємо наше розслідування, вивчаючи пов'язане з цим питання. Маючи на увазі, що швидкість може розглядатися як швидкість зміни положення, припустимо, що у нас є функція\(s(t)\), яка дає положення об'єкта вздовж осі координат в будь-який момент часу\(t\). Чи можемо ми використовувати ці самі ідеї для створення розумного визначення миттєвої швидкості в даний час\(t=a?\) Ми починаємо з наближення миттєвої швидкості із середньою швидкістю. По-перше, нагадаємо, що швидкість об'єкта, що рухається з постійною швидкістю, - це відношення пройденої відстані до відрізку пройденого ним часу. Визначено середню швидкість об'єкта за часовий проміжок, яка є зміною його положення, поділеною на довжину часового періоду.

Визначення: Середня швидкість

\(s(t)\)Дозволяти положення об'єкта, що рухається уздовж координатної осі в той час\(t\). Середня швидкість об'єкта за проміжок часу,\([a,t]\) де\(a<t\) (або\([t,a]\)\(t<a)\) якщо

\[v_{ave}=\dfrac{s(t)−s(a)}{t−a}. \label{avgvel} \]

Як\(t\) вибирається ближче до\(a\), середня швидкість стає ближче до миттєвої швидкості. Зауважте, що знаходження середньої швидкості функції позиції протягом часового інтервалу по суті таке ж, як знаходження нахилу січної лінії до функції. Крім того, щоб знайти нахил дотичної лінії в точці\(a\), ми дозволяємо\(x\) -значенням\(a\) наближатися до нахилу січної лінії. Аналогічно, щоб знайти миттєву швидкість в часі\(a\), ми дозволяємо\(t\) -значенням\(a\) наближатися до середньої швидкості. Цей процес дозволу\(x\) або\(t\) наближення\(a\) у виразі називається прийняттям межі. Таким чином, ми можемо визначити миттєву швидкість наступним чином.

Визначення: Миттєва швидкість

Для функції положення миттєва швидкість за один раз\(t=a\) - це величина\(s(t)\), до якої середні швидкості наближаються на інтервалах форми\([a,t]\) і в\([t,a]\) міру наближення\(t\) значень\(a\), за умови, що таке значення існує.

Приклад\(\PageIndex{2}\) ілюструє це поняття меж і середньої швидкості.

Приклад\(\PageIndex{2}\): Finding Average Velocity

Скеля скидається з висоти 64 футів. Визначено, що його висота (у футах) над землею t секунд пізніше (за\(0≤t≤2\)) задається\(s(t)=−16t^2+64\). Знайдіть середню швидкість породи за кожен із заданих часових інтервалів. Використовуйте цю інформацію, щоб вгадати миттєву швидкість породи в той час\(t=0.5\).

[\(0.49,0.5\)]
[\(0.5,0.51\)]

Рішення

Підставляємо дані в Equation\ ref {avgvel} для визначення середньої швидкості.

\[v_{ave}=\dfrac{s(0.49)−s(0.5)}{0.49−0.5}=−15.84 \nonumber \]
\[v_{ave}=\dfrac{s(0.51)−s(0.5)}{0.51−0.5}=−16.016 \nonumber \]

Миттєва швидкість становить десь від −15,84 до −16,16 футів/сек. Хорошою припущенням може бути −16 футів/сек.

Вправа\(\PageIndex{2}\)

Об'єкт рухається вздовж осі координат так, що його положення в часі\(t\) задається\(s(t)=t^3\). Оцініть його миттєву швидкість в часі,\(t=2\) обчисливши її середню швидкість за часовий інтервал [\(2,2.001\)].

Підказка: Використовуйте рівняння\ ref {avgvel} с\(v_{ave}=\dfrac{s(2.001)−s(2)}{2.001−2}\).

Відповідь: 12.006001

Задача про площу та інтегральне числення

Тепер звернемо увагу на класичний питання з числення. Багато величин у фізиці - наприклад, кількість роботи - можна інтерпретувати як область під кривою. Це змушує нас задати питання: Як ми можемо знайти площу між графіком функції та\(x\) -віссю через інтервал (Рисунок\(\PageIndex{7}\))?

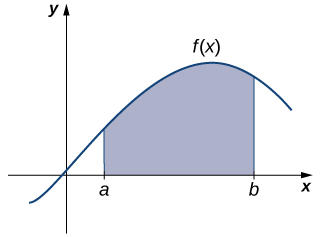
Показано графік загальної кривої функції f (x) у формі пагорба в квадранті. Область під функцією затінюється над віссю x та між x=a та x=b. — Малюнок\(\PageIndex{7}\): Проблема зони: Як знайти площу затіненої області?

Як і у відповіді на наші попередні питання по швидкості, спочатку спробуємо наблизити рішення. Наближаємо площу, розділивши вгору інтервал\([a,b]\) на менші проміжки у формі прямокутників. Наближення площі відбувається від складання площ цих прямокутників (рис.\(\PageIndex{8}\)).

Графік такий же, як і попереднє зображення, з однією відмінністю. Замість області, повністю затіненої під вигнутою функцією, інтервал [a, b] ділиться на менші інтервали у формі прямокутників. Прямокутники мають однакову невелику ширину. Висота кожного прямокутника - це висота функції в середині основи цього конкретного прямокутника. — Малюнок\(\PageIndex{8}\): Площа області під кривою наближається шляхом підсумовування площ тонких прямокутників.

Коли ширини прямокутників стають меншими (наближаються до нуля), суми площ прямокутників наближаються до площі між графіком\(f(x)\) і\(x\) -віссю за інтервал\([a,b]\). Знову ж таки, ми опиняємося, що приймаємо межу. Межі цього типу служать підставою для визначення певного інтеграла. Інтегральне числення - це вивчення інтегралів та їх застосувань.

Приклад\(\PageIndex{3}\): Estimation Using Rectangles

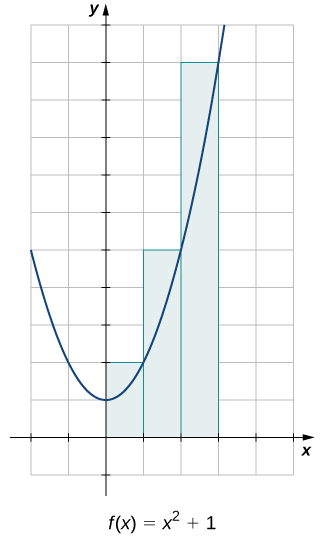
Оцініть площу між\(x\) -віссю та графіком\(f(x)=x^2+1\) над інтервалом за\([0,3]\) допомогою трьох прямокутників, показаних на малюнку\(\PageIndex{9}\).

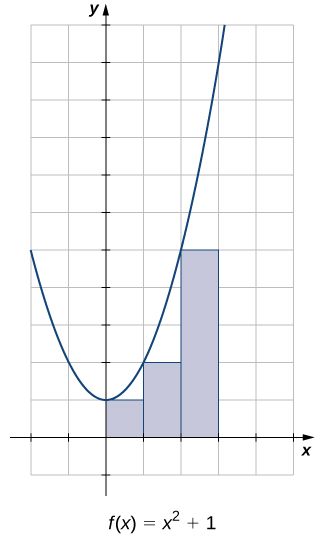
Графік параболи, що відкривається вгору з найнижчою точкою в (0,1). Прямокутник висотою 1, що простягається від x = 0 до x = 1, стосується параболи в точці (0,1); прямокутник висотою 2 від x=1 до x=2 торкається його в точці (1,2); прямокутник висотою 5 від x=2 до x=3 торкається його в точці (2,5) — Малюнок\(\PageIndex{9}\): Площа області під кривою\(f(x)=x^2+1\) може бути оцінена за допомогою прямокутників.

Рішення

Площі трьох прямокутників - 1 блок ², 2 блок ² і 5 блок ². Використовуючи ці прямокутники, наша оцінка площі становить 8 одиниця ².

Вправа\(\PageIndex{3}\)

Оцініть площу між\(x\) -віссю та графіком\(f(x)=x^2+1\) над інтервалом за\([0,3]\) допомогою трьох прямокутників, показаних на малюнку\(\PageIndex{10}\).

Графік параболи, що відкривається вгору, з найнижчою точкою у точці (0,1). Прямокутник висотою 2 і простягається від x = 0 до x = 1 торкається параболи в точці (1,2); прямокутник висотою 5 від x = 1 до x = 2 торкається його в точці (2,5); прямокутник висотою 10 від x = 2 до x = 3 торкається його в точці (3,10) — Малюнок\(\PageIndex{10}\): Площа області під кривою\(f(x)=x^2+1\) може бути оцінена за допомогою прямокутників.

Підказка: Використовуйте приклад\(\PageIndex{3}\) як орієнтир

Відповідь: 17\(\mathrm{unit}^2\)

Інші аспекти обчислення

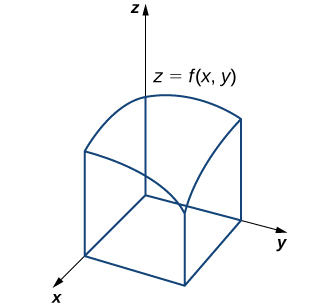
Поки що ми вивчали функції тільки однієї змінної. Такі функції можуть бути представлені візуально за допомогою графіків у двох вимірах, однак немає вагомих підстав обмежувати наше дослідження двома вимірами. Припустимо, наприклад, що замість визначення швидкості об'єкта, що рухається уздовж координатної осі, ми хочемо визначити швидкість породи, випущеної з катапульти в даний момент часу, або літака, що рухається в трьох вимірах. Ми могли б захотіти графікувати функції реальних значень двох змінних або визначити обсяги твердих тіл типу, показаного на малюнку\(\PageIndex{11}\). Це лише деякі з типів питань, на які можна задати і відповісти за допомогою багатоваріантного обчислення. Неофіційно багатозмінне числення можна охарактеризувати як дослідження числення функцій двох і більше змінних. Однак перш ніж досліджувати ці та інші ідеї, ми повинні спочатку закласти основу для вивчення числення в одній змінній, досліджуючи поняття межі.

Діаграма в тривимірному просторі, над осями x, y та z, де z = f (x, y). Основою є вісь x, y, а висота - вісь z. Основа являє собою прямокутник, що міститься в площині осі x, y. Верх - це поверхня змінної висоти з кутами, розташованими безпосередньо над кутами прямокутника в площині x, y.. Найвища точка знаходиться над кутом у x=0, y=0. Найнижча точка знаходиться в куті десь у першому квадранті площини x, y. Інші дві точки приблизно однакової висоти і розташовані над кутами на осі x та осі y. Проводяться лінії, що з'єднують кути прямокутника з кутами поверхні. — Малюнок\(\PageIndex{11}\): Ми можемо використовувати багатозмінне обчислення, щоб знайти об'єм між поверхнею, визначеною функцією двох змінних, і площиною.

Ключові поняття

Диференціальне числення виникло внаслідок спроби вирішити задачу визначення нахилу прямої дотичної до кривої в точці. Нахил дотичної лінії вказує на швидкість зміни функції, яку також називають похідною. Обчислення похідної вимагає знаходження межі.
Інтегральне числення виникло внаслідок спроби розв'язати задачу знаходження площі області між графіком функції та\(x\) -віссю. Ми можемо наблизити площу, розділивши її на тонкі прямокутники і підсумовуючи площі цих прямокутників. Таке підсумовування призводить до значення функції, яка називається інтегралом. Інтеграл також обчислюється шляхом знаходження межі і, по суті, пов'язаний з похідною функції.
Багатовимірне обчислення дозволяє вирішувати задачі в тривимірному просторі, включаючи визначення руху в просторі і знаходження обсягів твердих тіл.

Ключові рівняння

Нахил січної лінії

\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)

Середня швидкість за інтервалом [a, t]

\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)

Глосарій

середня швидкість: зміна положення об'єкта, поділене на довжину часового періоду; середня швидкість об'єкта за часовий проміжок [\(t,a\)] (if\(t<a\) або [\(a,t\)] if\(t>a\)), з позицією, заданою\(s(t)\), тобто\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)

диференціальне числення: область обчислення, що займається вивченням похідних та їх застосувань

миттєва швидкість: Миттєва швидкість об'єкта з функцією положення, яка задається, -\(s(t)\) це величина, до якої середні швидкості на інтервалах форми [\(t,a\)] і [\(a,t\)] наближаються як значення\(t\) переміщення ближче\(a\), за умови наявності такої величини

інтегральне числення: вивчення інтегралів та їх застосувань

межа: процес дозволу x або t наблизитися до а у виразі;\(f(x)\) межа функції як\(x\) підходи\(a\) - це значення, яке\(f(x)\) наближається як\(x\) підходи\(a\)

багатоваріантне обчислення: вивчення числення функцій двох і більше змінних

січний: Січна лінія до функції\(f(x)\) at\(a\) - це пряма через точку (\(a,f(a)\)) та іншу точку на функції; нахил січної лінії задається\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)

дотична: Дотична лінія до графіка функції в точці (\(a,f(a)\)) - це лінія, яка січні лінії через (\(a,f(a)\)) наближаються, коли вони приймаються через точки на функції з\(x\) -значеннями, які наближаються\(a\); нахил дотичної лінії до графіка при\(a\) вимірює швидкість зміни функція при\(a\)