5.4: Фундаментальна теорема числення

Last updated
Save as PDF

Page ID: 60717

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

$f(t)$Дозволяти бути безперервна функція, визначена на$[a,b]$. Певним інтегралом$\displaystyle \int_a^b f(x)\,dx$ є «область під$f $" на$[a,b]$. Ми можемо перетворити це поняття в функцію, дозволяючи верхню (або нижню) межу змінюватися.

Нехай$\displaystyle F(x) = \int_a^x f(t) \,dt$. Він обчислює площу під$f$ на$[a,x]$, як показано на малюнку$\PageIndex{1}$. Ми можемо вивчити цю функцію, використовуючи наші знання про певний інтеграл. Наприклад,$F(a)=0$ так як$\displaystyle \int_a^af(t) \,dt=0$.

$альт$

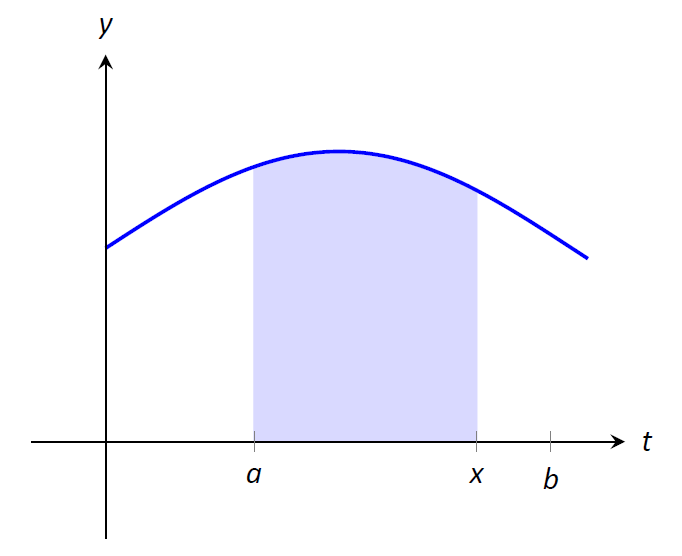
Малюнок$\PageIndex{1}$: Площа затіненої області дорівнює$\displaystyle F(x) = \int_a^x f(t) \,dt$.

Ми також можемо застосувати ідеї числення$F(x)$; зокрема, ми можемо обчислити його похідну. Хоча це може здатися нешкідливою справою, це має далекосяжні наслідки, про що свідчить той факт, що результат дається як важлива теорема.

Теорема$\PageIndex{1}$: The Fundamental Theorem of Calculus, Part 1

$f$Дозволяти бути безперервним$[a,b]$ і нехай$\displaystyle F(x) = \int_a^x f(t) \,dt$. Тоді$F$ є диференційованою функцією на$(a,b)$, і

\[F'(x)=f(x).\]

Спочатку це здається простим, як продемонстровано в наступному прикладі.

Приклад$\PageIndex{1}$: Using the Fundamental Theorem of Calculus, Part 1

Нехай$\displaystyle F(x) = \int_{-5}^x (t^2+\sin t) \,dt $. Що таке$F'(x)$?}

Рішення

Використовуючи фундаментальну теорему числення, ми маємо$F'(x) = x^2+\sin x$.

Цей простий приклад виявляє щось$F(x)$ неймовірне: є антипохідним$x^2+\sin x$! Тому$F(x) = \frac13x^3-\cos x+C$ для деякого значення$C$. (Ми можемо знайти$C$, але взагалі нам все одно. Ми знаємо це$F(-5)=0$, що дозволяє нам обчислювати$C$. В даному випадку,$C=\cos(-5)+\frac{125}3$.)

Ми зробили більше, ніж знайшли складний спосіб обчислення антидериватива. Розглянемо функцію,$f$ визначену на відкритому інтервалі$a$, що містить,$b$ і$c$. Припустимо, ми хочемо обчислити$\displaystyle \int_a^b f(t) \,dt$. По-перше, нехай$\displaystyle F(x) = \int_c^x f(t)\,dt $. Використовуючи властивості певного інтеграла, знайденого в теоремі 5.2.1, ми знаємо

\[ \begin{align}\int_a^b f(t) \,dt&= \int_a^c f(t) \,dt+ \int_c^b f(t) \,dt \\ &= -\int_c^a f(t) \,dt + \int_c^b f(t) \,dt \\ &=-F(a) + F(b)\\&= F(b) - F(a). \end{align}\]

Тепер ми бачимо, як пов'язані невизначені інтеграли та визначені інтеграли: ми можемо оцінити певний інтеграл за допомогою антипохідних! Це друга частина фундаментальної теореми числення.

Теорема$\PageIndex{2}$: The Fundamental Theorem of Calculus, Part 2

$f$Дозволяти бути безперервним$[a,b]$ і нехай$F$ буде будь-яке антипохідне від$f$. Тоді

\[\int_a^b f(x)\,dx = F(b) - F(a).\]

Приклад$\PageIndex{2}$: Using the Fundamental Theorem of Calculus, Part 2

Ми провели багато часу в попередньому розділі вивчення$\int_0^4(4x-x^2)\,dx$. Використовуючи фундаментальну теорему числення, оцініть цей певний інтеграл.

Рішення

Нам потрібен антидериватив від$f(x)=4x-x^2$. Всі антипохідні$f$ мають форму$F(x) = 2x^2-\frac13x^3+C$; для простоти вибирайте$C=0$.

Фундаментальна теорема станів числення

\[\int_0^4(4x-x^2)\,dx = F(4)-F(0) = \big(2(4)^2-\frac134^3\big)-\big(0-0\big) = 32-\frac{64}3 = 32/3.\]

Це та сама відповідь, яку ми отримали, використовуючи обмеження в попередньому розділі, просто з набагато меншою роботою.

Позначення: Спеціальне позначення часто використовується в процесі оцінки певних інтегралів за допомогою Фундаментальної теореми числення. Замість явного написання$F(b)-F(a)$$F(x)\Big|_a^b$ використовується позначення. Таким чином, рішення для$\PageIndex{2}$ Example буде записано як:

\[\int_0^4(4x-x^2)\,dx = \left.\left(2x^2-\frac13x^3\right)\right|_0^4 = \big(2(4)^2-\frac134^3\big)-\big(0-0\big) = 32/3.\]

Константа$C$: Будь-яка антипохідна$F(x)$ може бути обрана при використанні фундаментальної теореми числення для оцінки певного інтеграла, тобто будь-яке значення$C$ може бути підібрано. Константа завжди скасовує вираз при оцінці$F(b)-F(a)$, тому не має значення, яке значення підібрано. Це справа, ми могли б також дозволити$C=0$.

Приклад$\PageIndex{3}$: Using the Fundamental Theorem of Calculus, Part 2

Оцініть наступні певні інтеграли.

\[1.\ \int_{-2}^2 x^3\,dx \quad 2.\ \int_0^\pi \sin x\,dx \qquad 3.\ \int_0^5 e^t \,dt \qquad 4.\ \int_4^9 \sqrt{u}\ du\qquad 5.\ \int_1^5 2\,dx\]

Рішення

$\displaystyle \int_{-2}^2 x^3\,dx = \left.\frac14x^4\right|_{-2}^2 = \left(\frac142^4\right) - \left(\frac14(-2)^4\right) = 0.$
$\displaystyle \int_0^\pi \sin x\,dx = -\cos x\Big|_0^\pi = -\cos \pi- \big(-\cos 0\big) = 1+1=2.$
(Це цікаво; він говорить, що площа під одним «горбом» синусоїдальної кривої дорівнює 2.)
$\displaystyle \int_0^5e^t \,dt = e^t\Big|_0^5 = e^5 - e^0 = e^5-1 \approx 147.41.$
$ \displaystyle \int_4^9 \sqrt{u}\ du = \int_4^9 u^\frac12\ du = \left.\frac23u^\frac32\right|_4^9 = \frac23\left(9^\frac32-4^\frac32\right) = \frac23\big(27-8\big) =\frac{38}3.$
$\displaystyle \int_1^5 2\,dx = 2x\Big|_1^5 = 2(5)-2=2(5-1)=8.$

Цей інтеграл цікавий; integrand є постійною функцією, отже, ми знаходимо площу прямокутника з шириною$(5-1)=4$ та висотою 2. Зверніть увагу, як оцінка певного інтеграла призвела до$2(4)=8$.

Загалом, якщо$c$ константа, то$\displaystyle \int_a^b c\,dx = c(b-a)$.

Розуміння руху за допомогою фундаментальної теореми числення

Починаючи з Key Idea 1, ми встановили, що похідна функції положення є швидкісною функцією, а похідною функції швидкості є функція прискорення. Тепер розглянемо певні інтеграли функцій швидкості та прискорення. Зокрема, якщо$v(t)$ це функція швидкості, що$\displaystyle \int_a^b v(t) \,dt$ означає?

Фундаментальна теорема обчислення стверджує, що

\[\int_a^b v(t) \,dt = V(b) - V(a),\]

де$V(t)$ є будь-яке антипохідне від$v(t)$. Оскільки$v(t)$ є швидкісною функцією,$V(t)$ повинна бути функція положення, і$V(b) - V(a)$ вимірює зміну положення, або зміщення.

Приклад$\PageIndex{4}$: Finding displacement

М'яч кидається прямо вгору зі швидкістю, заданою$v(t) = -32t+20$ ft/s, де$t$ вимірюється в секундах. Знайти і інтерпретувати,$\displaystyle \int_0^1 v(t) \,dt.$}

Рішення

Використовуючи фундаментальну теорему числення, ми маємо

\[ \begin{align} \int_0^1 v(t) \,dt &= \int_0^1 (-32t+20) \,dt \\ &= -16t^2 + 20t\Big|_0^1 \\ &= 4. \end{align}\]

Таким чином, якщо м'яч кидається прямо в повітря зі швидкістю$v(t) = -32t+20$, висота м'яча, через 1 секунду, буде на 4 фути вище початкової висоти. (Зверніть увагу, що м'яч пройшов набагато далі. Він піднявся до свого піку і падає вниз, але різниця між його висотою на$t=0$ і$t=1$ становить 4 фути.

Інтеграція функції швидкості зміни дає загальну зміну. Швидкість - це швидкість зміни положення; інтеграційна швидкість дає загальну зміну положення, тобто зміщення.

Інтеграція функції швидкості дає подібний, хоча і інший результат. Швидкість - це також швидкість зміни положення, але не враховує напрямок. Таким чином, інтеграція функції швидкості дає повну зміну положення, без можливості «негативної зміни положення». Звідси інтеграл швидкісної функції дає пройдену відстань.

Оскільки прискорення - це швидкість зміни швидкості, інтеграція функції прискорення дає повну зміну швидкості. У нас немає простого терміна для цього аналога зміщення. Якщо$a(t) = 5 \text{ miles}/\text{h}^2 $ і$t$ вимірюється годинами, то

\[\int_0^3 a(t) \,dt = 15\]

означає, що швидкість збільшилася на 15 м/год від$t=0$ до$t=3$.

Фундаментальна теорема числення та правило ланцюга

Частина 1 фундаментальної теореми числення (FTC) стверджує, що дано$\displaystyle F(x) = \int_a^x f(t) \,dt$,$F'(x) = f(x)$. Використовуючи інші позначення,$ \frac{d}{\,dx}\big(F(x)\big) = f(x)$. Хоча ми щойно практикували оцінку певних інтегралів, іноді знайти антипохідні неможливо, і нам потрібно покладатися на інші методи, щоб наблизити значення певного інтеграла. Функції,$\displaystyle F(x) = \int_a^x f(t) \,dt$ написані як, корисні в таких ситуаціях.

Може бути корисним, щоб скласти таку функцію з іншою. Як приклад, ми можемо скласти$F(x)$ з,$g(x)$ щоб отримати

\[F\big(g(x)\big) = \int_a^{g(x)} f(t) \,dt.\]

Що таке похідна такої функції? Правило ланцюга може бути використано для держави

\[\frac{d}{\,dx}\Big(F\big(g(x)\big)\Big) = F'\big(g(x)\big)g'(x) = f\big(g(x)\big)g'(x).\]

Приклад допоможе нам розібратися в цьому.

Приклад$\PageIndex{4}$: The FTC, Part 1, and the Chain Rule

Знайдіть похідну від$\displaystyle F(x) = \int_2^{x^2} \ln t \,dt$.

Рішення

Ми можемо розглядати$F(x)$ як функцію, що$\displaystyle G(x) = \int_2^x \ln t \,dt$ складається з$g(x) = x^2$; тобто$F(x) = G\big(g(x)\big)$. Фундаментальна теорема обчислення стверджує, що$G'(x) = \ln x$. Правило ланцюга дає нам

\[\begin{align} F'(x) &= G'\big(g(x)\big) g'(x) \\ &= \ln (g(x)) g'(x) \\ &= \ln (x^2) 2x \\ &=2x\ln x^2 \end{align}\]

Зазвичай кроки, що$g(x)$ визначають$G(x)$ і пропускаються.

Практикуйте це ще раз.

Приклад$\PageIndex{5}$: The FTC, Part 1, and the Chain Rule

Знайдіть похідну від$\displaystyle F(x) = \int_{\cos x}^5 t^3 \,dt.$

Рішення

Зауважте, що$\displaystyle F(x) = -\int_5^{\cos x} t^3 \,dt$. Розглядається таким чином, похідна від$F$ прямолінійна:

\[F'(x) = \sin x \cos^3 x.\]

Площа між кривими

Розглянемо неперервні функції$f(x)$ і$g(x)$ визначені на$[a,b]$, де$f(x) \geq g(x)$ для всіх$x$ в$[a,b]$, як показано на малюнку$\PageIndex{2}$. Яка область затіненої області, обмежена двома кривими$[a,b]$?

$альт$ $альт$

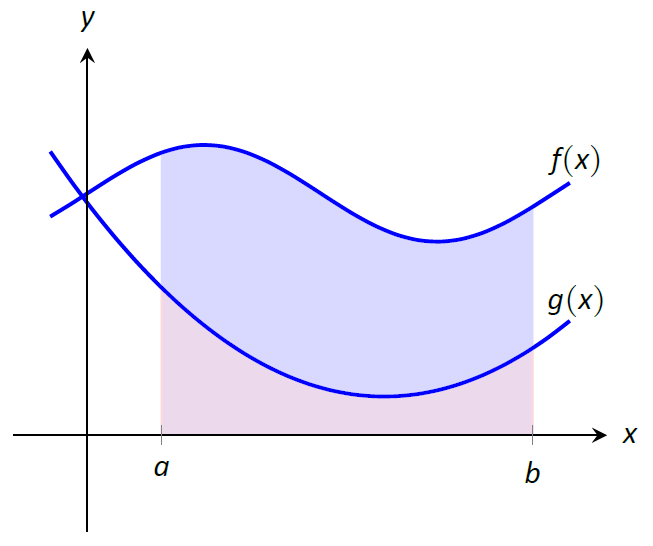
Малюнок$\PageIndex{2}$: Знаходження області, обмеженої двома функціями на інтервалі; це виявляється шляхом віднімання області під площею$f$.$g$

Місцевість можна знайти, визнавши, що ця область є «площею$f$$-$ під площею під»$g$. Використовуючи математичні позначення, площа

\[\int_a^b f(x)\,dx - \int_a^b g(x)\,dx.\]

Властивості певного інтеграла дозволяють спростити цей вираз до

\[ \int_a^b\big(f(x) - g(x)\big)\,dx.\]

Теорема$\PageIndex{3}$: Area Between Curves

$g(x)$Дозволяти$f(x)$ і бути безперервні функції, визначені на$[a,b]$ де$f(x)\geq g(x)$ для всіх$x$ в$[a,b]$. Площа області обмежена кривими$y=f(x)$,$y=g(x)$ а лініями$x=a$ і$x=b$ є

\[\int_a^b \big(f(x)-g(x)\big)\,dx.\]

Приклад$\PageIndex{6}$: Finding area between curves

Знайдіть площу області, обнесеної$y=x^2+x-5$ і$y=3x-2$.

Рішення

Це допоможе накидати ці дві функції, як це зроблено на малюнку$\PageIndex{3}$.

$альт$

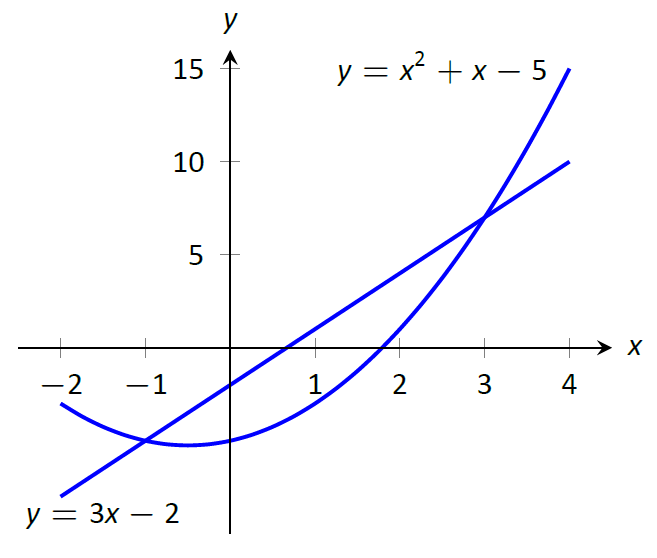
Малюнок$\PageIndex{3}$: Ескіз області, укладеної$y=x^2+x-5$ та$y=3x-2$ у прикладі$\PageIndex{6}$

Регіон, площа якого ми шукаємо, повністю обмежений цими двома функціями; вони, здається, перетинаються в$x=-1$ і$x=3$. Щоб перевірити, встановити$x^2+x-5=3x-2$ і вирішити для$x$:

\[\begin{align} x^2+x-5 &= 3x-2 \\ (x^2+x-5) - (3x-2) &= 0\\ x^2-2x-3 &= 0\\ (x-3)(x+1) &= 0\\ x&=-1,\ 3. \end{align}\]

Слідуючи теоремі$\PageIndex{3}$, площа

\[ \begin{align}\int_{-1}^3\big(3x-2 -(x^2+x-5)\big)\,dx &= \int_{-1}^3 (-x^2+2x+3)\,dx \\ &=\left.\left(-\frac13x^3+x^2+3x\right)\right|_{-1}^3 \\ &=-\frac13(27)+9+9-\left(\frac13+1-3\right)\\ &= 10\frac23 = 10.\overline{6} \end{align}\]

Теорема про середнє значення та середнє значення

$альт$

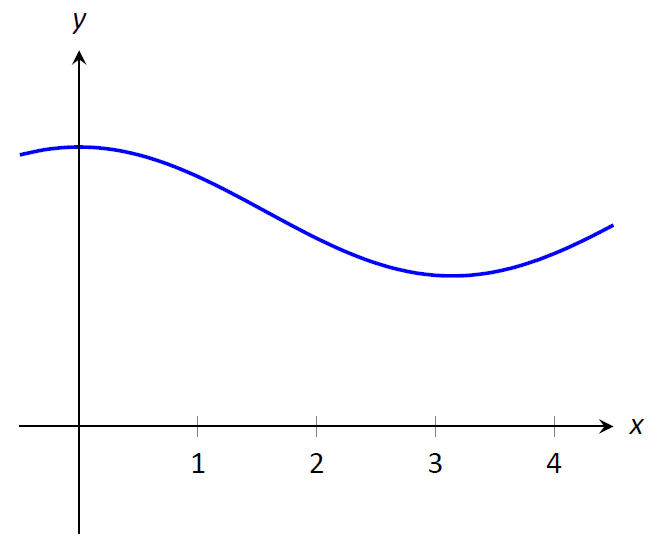
Рисунок$\PageIndex{4}$:$f$ Графік функції для введення теореми про середнє значення.

Розглянемо графік функції на$f$ малюнку$\PageIndex{4}$ та область, визначену$\displaystyle \int_1^4 f(x)\,dx$. Три прямокутника намальовані на малюнку$\PageIndex{5}$; в (а) висота прямокутника більше, ніж$f$ на$[1,4]$, отже, площа цього прямокутника більше, ніж$\displaystyle \int_0^4 f(x)\,dx$.

У (b) висота прямокутника менше, ніж$f$ на$[1,4]$, отже, площа цього прямокутника менше$\displaystyle \int_1^4 f(x)\,dx$.

$альт$ $альт$ $альт$

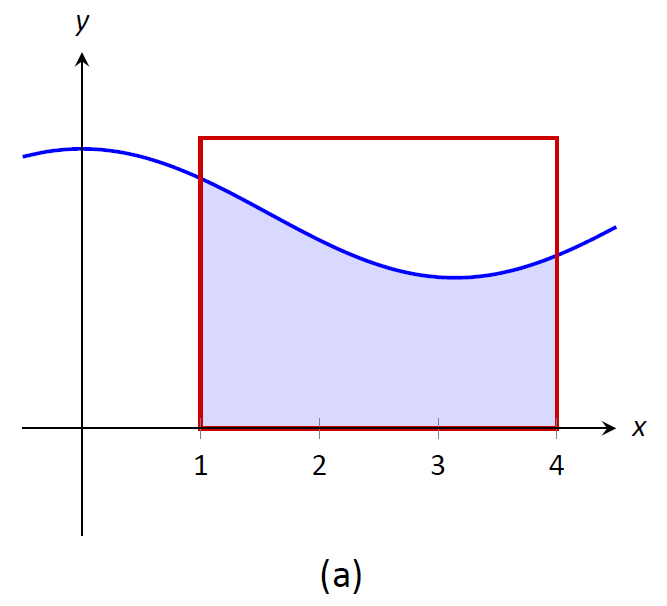
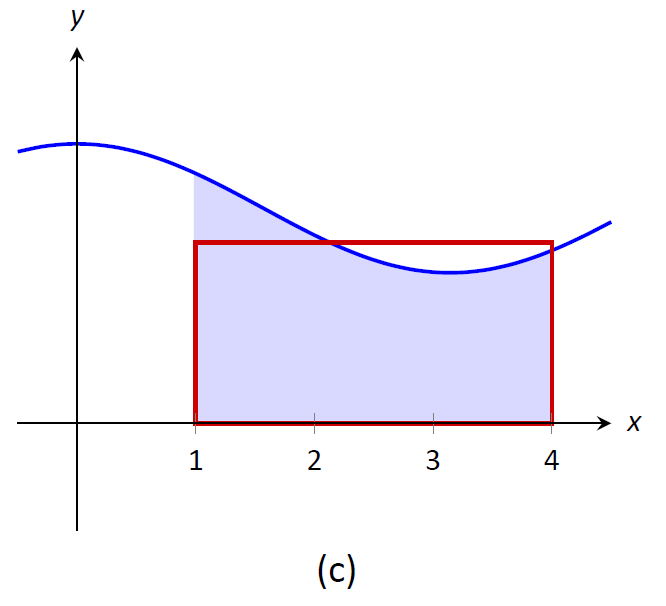
Малюнок$\PageIndex{5}$: Прямокутники різного розміру дають верхню та нижню межі$\displaystyle \int_1^4 f(x)\,dx$; останній прямокутник точно відповідає площі.

Нарешті, в (c) висота прямокутника така, що площа прямокутника точно така, що$\displaystyle \int_0^4 f(x)\,dx$. Оскільки прямокутники, які є «занадто великими», як у (a), і прямокутники, які «занадто мало», як у (b), дають області більші/менше$\displaystyle \int_1^4 f(x)\,dx$, ніж, має сенс, що існує прямокутник, вершина якого перетинається$f(x)$ десь на$[1,4]$, площа якого точно така, як у визначеного інтеграла.

Ми викладати цю ідею формально в теоремі.

Теорема$\PageIndex{4}$: The Mean Value Theorem of Integration

$f$Дозволяти бути безперервним на$[a,b]$. Існує значення$c$ в$[a,b]$ такому, що

\[\int_a^bf(x)\,dx = f(c)(b-a).\]

Це екзистенціальне твердження;$c$ існує, але ми не надаємо методу його знаходження. Теорема безпосередньо$\PageIndex{4}$ пов'язана з теоремою про середнє значення диференціювання, наведеної як теорема 3.2.1; ми залишаємо її читачеві, щоб побачити, як.

Ми демонструємо принципи, що беруть участь у цій версії теореми про середнє значення у наступному прикладі.

Приклад$\PageIndex{7}$: Using the Mean Value Theorem

Розглянемо$\displaystyle \int_0^\pi \sin x\,dx$. Знайдіть значення,$c$ гарантоване теоремою про середнє значення.

Рішення

Насамперед треба оцінити$\displaystyle \int_0^\pi \sin x\,dx$. (Це було зроблено раніше в прикладі$\PageIndex{3}$)

\[\int_0^\pi\sin x\,dx = -\cos x \Big|_0^\pi = 2.\]

Таким чином, ми шукаємо значення$c$ в$[0,\pi]$ такому, що$\pi\sin c =2$.

\[\pi\sin c = 2\ \ \Rightarrow\ \ \sin c = 2/\pi\ \ \Rightarrow\ \ c = \arcsin(2/\pi) \approx 0.69.\]

$альт$

Малюнок$\PageIndex{6}$: Графік$y=\sin x$ включення$[0,\pi]$ та прямокутника, гарантований теоремою про середнє значення.

На малюнку$\PageIndex{6}$$\sin x$ накидається разом з прямокутником з висотою$\sin (0.69)$. Площа прямокутника така ж, як і площа під$\sin x$ на$[0,\pi]$.

$f$Дозволяти бути функція на$[a,b]$ з$c$ таким, що$\displaystyle f(c)(b-a) = \int_a^bf(x)\,dx$. Розглянемо$\displaystyle \int_a^b\big(f(x)-f(c)\big)\,dx$:

\[\begin{align} \int_a^b\big(f(x)-f(c)\big)\,dx &= \int_a^b f(x) - \int_a^b f(c)\,dx\\ &= f(c)(b-a) - f(c)(b-a) \\ &= 0. \end{align}\]

При$f(x)$$-f(c)$ зміщенні на величину площі під$f$$x$ віссю -на$[a,b]$ таке ж, як і величина площі нижче$x$ -осі вище$f$; див. Рисунок$\PageIndex{7}$ для ілюстрації цього. У цьому сенсі можна сказати, що$f(c)$ це середнє значення$f$ на$[a,b]$.

$альт$ $альт$

Малюнок$\PageIndex{7}$: Ліворуч графік$y=f(x)$ та прямокутник, гарантований теоремою про середнє значення. Справа$y=f(x)$ зсувається вниз на$f(c)$; отримана «площа під кривою» дорівнює 0.

Значення$f(c)$ - середнє значення в іншому сенсі. По-перше, визнайте, що теорема про середнє значення може бути переписана як

\[f(c) = \frac{1}{b-a}\int_a^b f(x)\,dx,\]

для деякого значення$c$ в$[a,b]$. Далі розділіть інтервал$[a,b]$ на$n$ однаково розташовані підінтервали,$a=x_1 < x_2 < \ldots < x_{n+1}=b$ і виберіть будь-який$c_i$ в$[x_i,x_{i+1}]$. Середнє значення чисел$f(c_1)$,$f(c_2)$,$\ldots$,$f(c_n)$ становить:

\[\frac1n\Big(f(c_1) + f(c_2) + \ldots + f(c_n)\Big) = \frac1n\sum_{i=1}^n f(c_i).\]

Помножте цей останній вираз на 1 у вигляді$\frac{(b-a)}{(b-a)}$:

\[ \begin{align} \frac1n\sum_{i=1}^n f(c_i) &= \sum_{i=1}^n f(c_i)\frac1n \\ &= \sum_{i=1}^n f(c_i)\frac1n \frac{(b-a)}{(b-a)} \\ &=\frac{1}{b-a} \sum_{i=1}^n f(c_i)\,\Delta x\quad \text{(where $\Delta x = (b-a)/n$)} \end{align}\]

Тепер візьміть ліміт як$n\to\infty$:

\[\lim_{n\to\infty} \frac{1}{b-a} \sum_{i=1}^n f(c_i)\,\Delta x\quad = \quad \frac{1}{b-a} \int_a^b f(x)\,dx\quad = \quad f(c).\]

Це говорить нам про це: коли ми оцінюємо$f$ в$n$ (дещо) однаково розташованих точках$[a,b]$, середнє значення цих зразків є$f(c)$ як$n\to\infty$.

Це призводить нас до визначення.

Визначення$\PageIndex{1}$: The Average Value of $f$ on $[a,b]$

$f$Дозволяти бути безперервним на$[a,b]$. Середнє значення$f$ on$[a,b]$ - це$f(c)$, де$c$ значення в$[a,b]$ гарантованому теоремою про середнє значення. Тобто,

\[\text{Average Value of $f$ on $[a,b]$} = \frac{1}{b-a}\int_a^b f(x)\,dx.\]

Застосування цього визначення наведено в наступному прикладі.

Приклад$\PageIndex{8}$: Finding the average value of a function

Об'єкт рухається вперед і назад по прямій зі швидкістю, заданою$v(t) = (t-1)^2$ на$[0,3]$, де$t$ вимірюється в секундах і$v(t)$ вимірюється в футів/с.

Яка середня швидкість руху об'єкта?

Рішення

За нашим визначенням середня швидкість дорівнює:

\[\frac{1}{3-0}\int_0^3 (t-1)^2 \,dt =\frac13 \int_0^3 \big(t^2-2t+1\big) \,dt = \left.\frac13\left(\frac13t^3-t^2+t\right)\right|_0^3 = 1\text{ ft/s}.\]

Ми можемо зрозуміти вищевказаний приклад через більш просту ситуацію. Припустимо, ви проїхали 100 миль за 2 години. Якою була ваша середня швидкість? Відповідь проста:$\text{displacement}/\text{time} = 100 \;\text{miles}/2\;\text{hours} = 50 mph$.

Яким було зміщення об'єкта в прикладі$\PageIndex{8}$? Ми обчислюємо це шляхом інтеграції його швидкісної функції:$\displaystyle \int_0^3 (t-1)^2 \,dt = 3$ ft. Його кінцеве положення становило 3 фути від початкового положення через 3 секунди: його середня швидкість становила 1 фут/с.

Цей розділ заклав основу для великої кількості великої математики, яку слід дотримуватися. Найважливіший урок полягає в наступному: певні інтеграли можна оцінити за допомогою антипохідних. Оскільки попередній розділ встановив, що певні інтеграли є межею сум Рімана, ми можемо згодом створити суми Рімана до наближених значень, відмінних від «площі під кривою», перетворити суми в певні інтеграли, а потім оцінити їх за допомогою Фундаментальної теореми числення. Це дозволить нам обчислити роботу, виконану змінною силою, об'ємом певних твердих тіл, довжиною дуги кривих тощо.

Мінус полягає в наступному: взагалі кажучи, обчислення антипохідних набагато складніше, ніж обчислення похідних. Наступна глава присвячена методам знаходження антипохідних, щоб можна було оцінити найрізноманітніші певні інтеграли. Перед цим у наступному розділі досліджуються методи наближення значення визначених інтегралів за межами правил Лівої руки, Правої руки та Середньої точки.