5.2: Певний інтеграл

Last updated
Save as PDF

Page ID: 60712

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Почнемо з легкої проблеми. Об'єкт рухається по прямій лінії з постійною швидкістю 5 футів/с протягом 10 секунд. Наскільки далеко від своєї відправної точки знаходиться об'єкт?

Підходимо до цієї задачі зі знайомим рівнянням «$\times$Час$=$ швидкості відстані». У цьому випадку відстань = 5ft/s$\times$ 10s$=$ 50 футів.

Цікаво відзначити, що це рішення 50 футів можна представити графічно. Розглянемо малюнок$\PageIndex{1}$, де на осях зображена постійна швидкість 5ft/s. Затінення площі під лінією від$t=0$ до$t=10$ дає прямокутник площею 50 квадратних одиниць; коли розглядати одиниці осей, можна сказати, що ця площа становить 50 футів.

$альт$

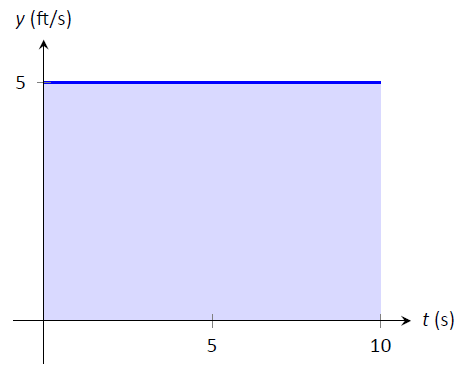
Малюнок$\PageIndex{1}$: Площа під функцією постійної швидкості відповідає пройденій відстані.

Тепер розглянемо трохи складнішу ситуацію (і не особливо реалістичну): об'єкт рухається по прямій з постійною швидкістю 5ft/s протягом 10 секунд, потім миттєво змінює курс зі швидкістю 2ft/s протягом 4 секунд. (Оскільки об'єкт рухається у зворотному напрямку при зворотному курсі, ми говоримо, що швидкість є постійною$-2$ ft/s.) Наскільки далеко від початкової точки знаходиться об'єкт — яке його зміщення?

Тут ми використовуємо «$_1$$\times$Час$=$ швидкості відстані$_1$ +$_2$$\times$ Час ставки»$_2$, який

\[\text{Distance } \ = 5\cdot10 + (-2)\cdot 4 = 42\text{ ft.}\]

Отже, об'єкт знаходиться в 42 футах від його початкового місця.

Ми можемо знову зобразити цю ситуацію графічно. На малюнку$\PageIndex{3}$ ми маємо швидкості, позначені як прямі лінії на$[0,10]$ і$[10,14]$, відповідно. Зсув об'єкта є

\[\text{"Area above the $t$--axis} \quad - \quad \text{Area below the $t$-axis,} \]

який легко обчислити як$50-8=42$ ноги.

$альт$

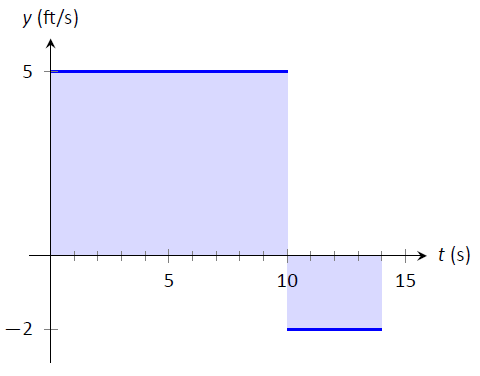
Малюнок$\PageIndex{2}$: Загальним зміщенням є область над$t$ віссю —мінус площа нижче$t$ осі —.

Тепер розглянемо більш складну проблему.

Приклад$\PageIndex{1}$: Finding position using velocity

Швидкість об'єкта, що рухається прямо вгору/вниз під прискоренням сили тяжіння$v(t) = -32t+48$,$t$ задається як, де час задається в секундах$t=0$, а швидкість - в футів/с.

Якою була початкова швидкість об'єкта?
Якою була максимальна висота об'єкта?
Якою була висота об'єкта в той час$t=2$?

Рішення

Це просто знайти початкову швидкість; в той час$t=0$,$v(0) =-32\cdot 0+48 = 48$ ft/s.

Щоб відповісти на питання про висоту об'єкта, нам потрібно знайти функцію положення об'єкта$s(t)$. Це початкова величина завдання, яку ми вивчали в попередньому розділі. Нам кажуть, що початкова висота дорівнює 0, тобто$s(0) = 0$. Ми знаємо$s'(t) = v(t) = -32t+48$. Щоб знайти$s$, знайдемо невизначений інтеграл$v(t)$:

\[\int v(t)\ dt = \int (-32t+48)\ dt = -16t^2+48t+C = s(t).\]

Оскільки$s(0) = 0$, робимо висновок, що$C=0$ і$s(t) = -16t^2+48t$.

Щоб знайти максимальну висоту об'єкта, нам потрібно знайти максимум$s$. Згадуючи нашу роботу з пошуку екстремальних значень, знаходимо критичні точки,$s$ встановивши її похідну рівну 0 і вирішивши для$t$:

\[s'(t) = -32t+48 = 0 \quad \Rightarrow \quad t=48/32 = 1.5\text{s}.\]

(Зверніть увагу, як ми закінчилися просто знайти, коли швидкість була 0ft/s!) Перший тест похідної показує, що це максимум, тому максимальна висота об'єкта знаходиться на

\[s(1.5) = -16(1.5)^2+48(1.5)=36\text{ft}.\]

Висота в часі$t=2$ тепер просто обчислити: вона$s(2) = 32$ футів.

Поки ми відповіли на всі три питання, давайте розглянемо їх ще раз графічно, використовуючи поняття області, які ми досліджували раніше.

$\PageIndex{3}$На малюнку зображений графік$v(t)$ по осях від$t=0$ до$t=3$. Це знову просто знайти$v(0)$. Як ми можемо використовувати графік, щоб знайти максимальну висоту об'єкта?

$альт$

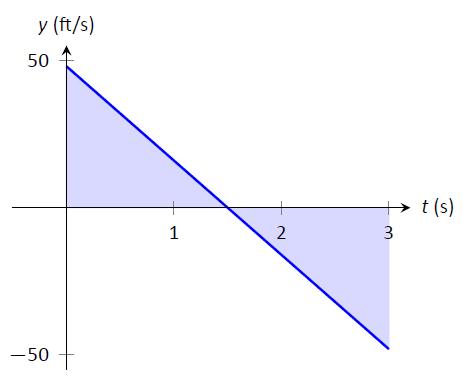
Малюнок$\PageIndex{3}$: Графік$v(t)=-32t+48$; затінені ділянки допомагають визначити зміщення.

Нагадаємо, як в нашій попередній роботі зміщення об'єкта (в даному випадку його висота) було виявлено як площа під кривою швидкості, як затінена на малюнку. Більше того, площа між кривою та$t$ віссю —, яка знаходиться нижче$t$ осі —, вважається «негативною» областю. Тобто він являє собою об'єкт, що повертається у вихідне положення. Отже, щоб знайти максимальну відстань від початкової точки - максимальну висоту - ми знаходимо область під лінією швидкості, яка знаходиться над$t$ віссю —, тобто від$t=0$ до$t=1.5$. Ця область являє собою трикутник; його площа

\[\text{Area } = \frac12\text{Base} \times \text{Height} =\frac12\times 1.5\text{s}\times 48\text{ft/s} = 36\text{ft},\]

який відповідає нашому попередньому розрахунку максимальної висоти.

Нарешті, ми знаходимо загальну підписану область під функцією швидкості від$t=0$$t=2$ до, щоб знайти$s(2)$, висоту на$t=2$, яка є зміщенням, відстань від поточного положення до вихідного положення. Тобто,

\[ \text{Displacement} = \text{Area above the $t-$axis} - \text{Area below $t$-axis.}\]

Регіони трикутники, і ми знаходимо

$\ текст {Зсув} =\ frac12 (1.5\ текст {s}) (48\ текст {ft/s}) -\ frac12 (.5\ текст {s}) (16\ текст {ft/s}) = 32\ текст {ft}.\]

Це також відповідає нашому попередньому розрахунку висоти на$t=2$.

Зверніть увагу, як ми відповіли на кожне питання в цьому прикладі двома способами. Наш перший метод полягав у маніпулюванні рівняннями, використовуючи наше розуміння антипохідних та похідних. Другий наш метод був геометричним: ми відповідали на питання, дивлячись на графік і знаходячи області певних областей цього графіка.

Наведений вище приклад не доводить зв'язок між площею під функцією швидкості та зміщенням, але це означає, що зв'язок існує. Розділ 5.4 дозволить повністю встановити факт, що ділянка під функцією швидкості є зміщенням.

Враховуючи графік функції$y=f(x)$, ми виявимо, що існує велика користь для обчислення площі між кривою$y=f(x)$ та$x$ -віссю. Через це нам потрібно визначити деякі терміни.

Визначення$\PageIndex{1}$: The Definite Integral, Total Signed Area

$y=f(x)$Дозволяти визначатися на замкнутому інтервалі$[a,b]$. Загальна підписана площа від$x=a$ до$x=b$ під$f$ становить:

\[(\text{area under $f$ and above the $x$-axis on $[a,b]$)}. - (\text{area above $f$ and under the $x$-axis on $[a,b]$}). \]

Певний інтеграл$f$ on$[a,b]$ - загальна знакова площа$f$ on$[a,b]$, що позначається

\[\int_a^b f(x)\ dx,\]

Є$a$ і$b$ є межі інтеграції.

За нашим визначенням, певний інтеграл дає «підписану область під»$f$. Ми зазвичай скидаємо слово «signed», коли говоримо про певний інтеграл, і просто сказати, що певний інтеграл дає «площа під$f$\,» або, частіше, «площа під кривою».

Попередній розділ ввів невизначений інтеграл, який ставився до антипохідних. Тепер ми визначили певний інтеграл, який відноситься до областей під функцією. Ці два дуже пов'язані, як ми побачимо, коли ми дізнаємося фундаментальну теорему обчислення в розділі 5.4. Нагадаємо, що раніше ми говорили, що символ$\int$ "" - це «подовжений S», який представляв знаходження «суми». У контексті певного інтеграла це позначення має трохи більше сенсу, оскільки ми складаємо області під функцією$f$.

Практикуємо використання цього позначення.

Приклад$\PageIndex{2}$: Evaluating definite integrals

Розглянемо функцію,$f$ наведену на рис$\PageIndex{4}$.

$альт$

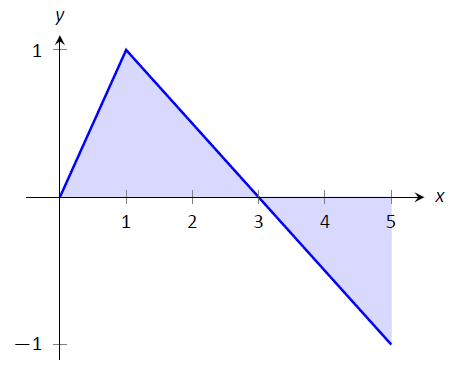
Малюнок$\PageIndex{4}$: Графік$f(x)$ у прикладі$2$

Знайти:

$\int_0^3 f(x)\ dx$
$\int_3^5 f(x)\ dx$
$\int_0^5 f(x)\ dx$
$\int_0^3 5f(x)\ dx$
$\int_1^1 f(x) \ dx$

Рішення

$\int_0^3 f(x) dx$це область під$f$ на проміжку$[0,3]$. Ця область є трикутником, тому площа є$\int_0^3 f(x) dx=\frac12(3)(1) = 1.5$.
$\int_3^5 f(x) dx$являє собою площу трикутника, знайденого під$x$ віссю —on$[3,5]$. Область є$\frac12(2)(1) = 1$; оскільки вона знаходиться під$x$ віссю —, це «негативна область». Тому$\int_3^5 f(x)\ dx = -1$.
$\int_0^5f(x) dx$є загальною підписаною площею під$f$ на$[0,5]$. Це і є$1.5 + (-1) = 0.5$.
$ \int_0^35f(x) dx$це область під$5f$ на$[0,3]$. Це намальовано на малюнку$\PageIndex{5}$. Знову ж таки, область - це трикутник, висота якого в 5 разів перевищує висоту вихідного трикутника. Таким чином площа$\int_0^35f(x)\ dx = 15/2 = 7.5.$

$альт$

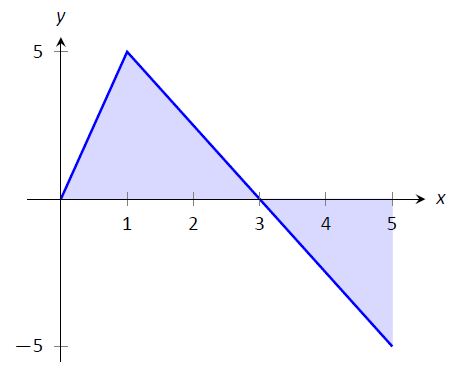
Малюнок$\PageIndex{5}$: Графік$5f$ у прикладі$\PageIndex{2}$. (Так, це виглядає так само, як графік на$f$ малюнку$\PageIndex{4}$, просто з іншим$y$ -масштабом.)

$\int_1^1f(x) dx$це область під$f$ на «інтервалі»$[1,1]$. Це описує відрізок лінії, а не область; він не має ширини. Тому площа дорівнює 0.

Цей приклад ілюструє деякі властивості певного інтеграла, наведені тут.

Теорема$\PageIndex{2}$: Properties of the Definite Integral

$f$$g$Дозволяти і визначатися на замкнутому інтервалі,$I$ який містить значення$a$,$b$ і$c$, і нехай$k$ бути константою. Наступні трюми:

$\int_a^a f(x) dx = 0$
$\int_a^b f(x) dx + \int_b^c f(x) dx = \int_a^cf(x) dx$
$\int_a^bf(x) dx = -\int_b^a f(x) dx$
$\int_a^b\big(f(x)\pm g(x)\big) dx = \int_a^bf(x)\ dx \pm \int_a^bg(x) dx$
$\int_a^bk\cdot f(x) dx = k\cdot\int_a^bf(x) dx$

Наведемо коротке обґрунтування теореми$\PageIndex{2}$ тут.

Як показано в прикладі$\PageIndex{2}$, немає «області під кривою», коли область не має ширини; отже, цей певний інтеграл дорівнює 0.
Це говорить про те, що загальна площа - це сума площ субрегіонів. Це легко розглянути, коли ми пускаємо$a<b<c$. Ми можемо$[a,c]$ розбити інтервал на два підінтервали,$[a,b]$ і$[b,c]$. Загальна площа над$[a,c]$ площею понад$[a,b]$ плюс площа над$[b,c]$.
Важливо зазначити, що це все ще справедливо, навіть якщо$a<b<c$ це не так. Про це ми обговоримо в наступному пункті.
Ця властивість може розглядатися як просто конвенція, щоб інші властивості працювали добре. (Пізніше ми побачимо, як ця властивість має обгрунтування все своє, не обов'язково на підтримку інших властивостей.) Припустимо$b<a<c$. Обговорення з попереднього пункту чітко виправдовує\[\int_b^a f(x) dx + \int_a^c f(x)\ dx = \int_b^c f(x) dx.\]
Однак, ми все ще стверджуємо, що, як спочатку було сказано,\[\int_a^b f(x)\ dx + \int_b^c f(x)\ dx = \int_a^c f(x)\ dx.\]
Як рівняння$\PageIndex{11}$ і$\PageIndex{12}$ пов'язані? Почніть з рівняння$\PageIndex{11}$:\[\begin{align} \int_b^a f(x) dx + \int_a^c f(x) dx &= \int_b^c f(x) dx\\ \int_a^c f(x)\ dx &= -\int_b^a f(x) dx + \int_b^c f(x) dx \end{align}\]
Властивість$(3)$ виправдовує зміну знака та перемикання меж інтеграції на$-\int_b^a f(x) dx$ термін; коли це зроблено, Рівняння$\PageIndex{11}$ і$\PageIndex{12}$ еквівалентні.
Висновок такий: прийнявши конвенцію про майно (3), Власність (2) має незалежно від порядку$a$,$b$ і$c$. Знову ж таки, в наступному розділі ми побачимо ще одне обгрунтування цієї властивості.
5,5. Кожен з них може бути неінтуїтивним. Властивість (5) стверджує, що при масштабуванні функції, наприклад, 7, площа замкнутої області також масштабується в 7 разів. Обидва властивості (4) і (5) можуть бути доведені за допомогою геометрії. Деталі не складні, але тут не обговорюються.

Приклад$\PageIndex{3}$: Evaluating definite integrals using Theorem $\PageIndex{2}$.

Розглянемо графік функції,$f(x)$ показаний на малюнку$\PageIndex{6}$.

$альт$

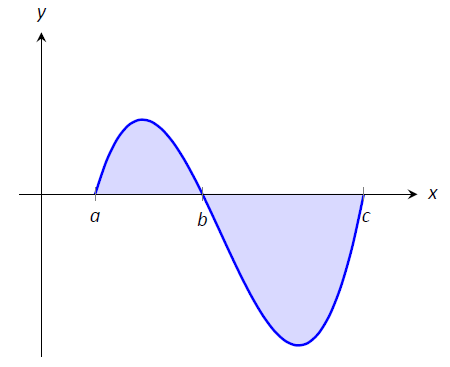
Малюнок$\PageIndex{6}$: Графік функції у прикладі$\PageIndex{3}$

Дайте відповідь на наступне:

Яке значення більше:$\int_a^b f(x) dx$ або$ \int_b^c f(x) dx$?
$\int_a^c f(x) dx$Більше або менше 0?
Яке значення більше:$\int_a^b f(x) dx$ або$\int_c^b f(x) dx$?

Рішення

$\int_a^b f(x) dx$має додатне значення (оскільки область знаходиться над$x$ віссю —), тоді як$\int_b^c f(x) dx$ має від'ємне значення. Отже$\int_a^b f(x) dx$, більше.
$\int_a^c f(x) dx$є загальною підписаною площею$f$ між$x=a$ і$x=c$. Оскільки область під$x$ віссю —виглядає більшою за область вище, ми робимо висновок, що певний інтеграл має значення менше 0.
Зверніть увагу, як другий інтеграл має межі «зворотні». Тому$\int_c^b f(x) dx$ являє собою додатне число, більше площі, описаної першим визначеним інтегралом. $\int_c^b f(x) dx$Звідси і більше.

Визначення площі певного інтеграла дозволяє за допомогою геометрії обчислити певний інтеграл деяких простих функцій.

Приклад$\PageIndex{4}$: Evaluating definite integrals using geometry

Оцініть наступні визначені інтеграли:

\[1. \ \int_{-2}^5 (2x-4)\ dx \qquad 2.\ \int_{-3}^3 \sqrt{9-x^2}\ dx.\]

Рішення

$альт$ $альт$

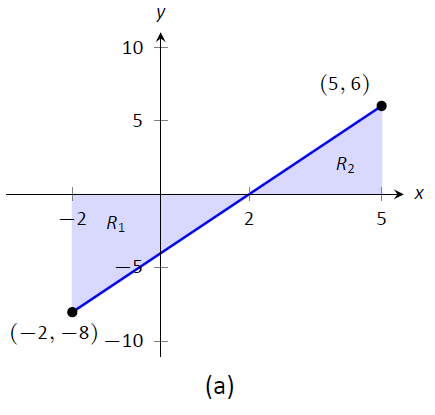
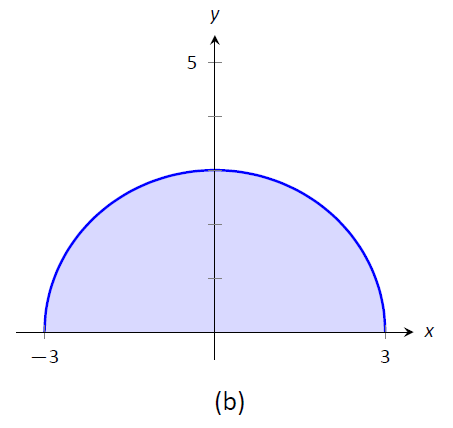
Рисунок$\PageIndex{7}$: Графік$f(x) = 2x-4$ in (a) та$f(x) = \sqrt{9-x^2}$ in (b), з Прикладу$\PageIndex{4}$

Корисно зробити ескіз функції в integrand, як показано на малюнку$\PageIndex{7a}$. Ми бачимо, що нам потрібно обчислити області двох областей, які ми позначили$R_1$ і$R_2$. Обидва трикутники, тому обчислення площі є простим: $$R_1:\ frac12 (4) (8) = 16\ qquad R_2:\ frac12 (3) 6 = 9.$$ Регіон$R_1$ лежить під$x$ віссю —, отже, вона вважається негативною областю (ми можемо вважати висоту трикутника "$-8$«), тому $$\ int_ {-2} ^5 (2x-4) дх = -16+9 = -7. $$
Визнайте, що цілісність цього певного інтеграла описує половину кола, як намальовано на малюнку$\PageIndex{7b}$, з радіусом 3. Таким чином, площа становить:

$\ int_ {-3} ^3\ sqrt {9-x^2}\ dx =\ фрак12\ пі r^2 =\ гідророзриву 92\ пі.\]

Приклад$\PageIndex{5}$: Understanding motion given velocity

Розглянемо графік швидкісної функції об'єкта, що рухається по прямій лінії, наведений на малюнку$\PageIndex{8}$, де числа в заданих областях дають площу цієї області. Припустимо, що певний інтеграл швидкісної функції дає зсув. Знайти максимальну швидкість об'єкта і його максимальне зміщення з вихідного положення.

Рішення

$альт$

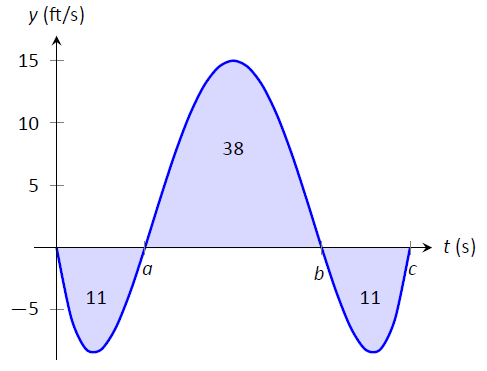
Малюнок$\PageIndex{8}$: Графік швидкості у прикладі$\PageIndex{5}$.

Оскільки графік дає швидкість, знайти максимальну швидкість просто: вона виглядає як 15ft/s.

За часом$t=0$ зміщення дорівнює 0; об'єкт знаходиться в початковому положенні. За час$t=a$ об'єкт перемістився назад на 11 футів. Між часом$t=a$ і$t=b$ об'єкт рухається вперед на 38 футів, приводячи його в положення на 27 футів вперед від початкового положення. Від$t=b$ до$t=c$ об'єкта знову рухається назад, отже його максимальне зміщення становить 27 футів від початкового положення.

У наших прикладах ми або знайшли області областей, які мають приємні геометричні фігури (такі як прямокутники, трикутники та кола), або ділянки були надані нам. Розглянемо малюнок$\PageIndex{9}$, де область нижче$y=x^2$ затінена. Яка його площа? Функція відносно$y=x^2$ проста, але форма, яку вона визначає, має область, яку не просто знайти геометрично.

$альт$

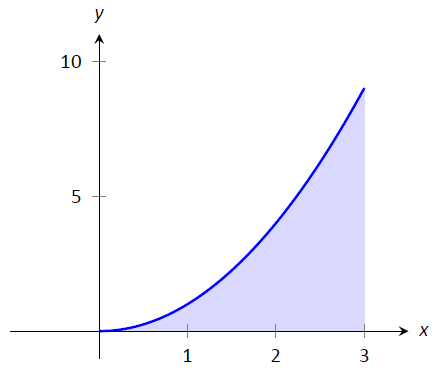
Малюнок$\PageIndex{9}$: Яка область нижче$y=x^2$ на$[0,3]$? Область - це не звичайна геометрична форма.

У наступному розділі ми розглянемо, як знайти райони таких регіонів.