4.3: Оптимізація

Last updated
Save as PDF

Page ID: 60672

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У розділі 3.1 ми дізналися про екстремальні значення — найбільші та найменші значення, які функція досягає на інтервалі. Ми мотивували наш інтерес до таких цінностей, обговорюючи, як має сенс хотіти знати найвищие/найнижчі значення запасу, або найшвидший/найповільніший об'єкт рухався. У цьому розділі ми застосовуємо поняття екстремальних значень для вирішення «словових задач», тобто задач, заявлених в терміні ситуацій, які вимагають від нас створення відповідної математичної основи, в якій вирішувати задачу.

Почнемо з класичного прикладу, за яким слід обговорення теми оптимізації.

Приклад$\PageIndex{1}$: Optimization: perimeter and area

Людина має 100 футів огорожі, великий двір і маленька собака. Він хоче створити прямокутний вольєр для своєї собаки з огорожею, що забезпечує максимальну площу. Які розміри забезпечують максимальну площу?

Рішення

Ймовірно, можна вгадати правильну відповідь - це чудово. Ми продовжимо показувати, як обчислення може надати цю відповідь у контексті, який доводить, що ця відповідь є правильною.

Допомагає скласти ескіз ситуації. Наш корпус намальований двічі на малюнку$\PageIndex{1}$, або зеленою травою та гарними дошками паркану, або як простий прямокутник. Так чи інакше, малювання прямокутника змушує нас усвідомити, що нам потрібно знати розміри цього прямокутника, щоб ми могли створити функцію області - врешті-решт, ми намагаємося максимізувати площу.

$альт$

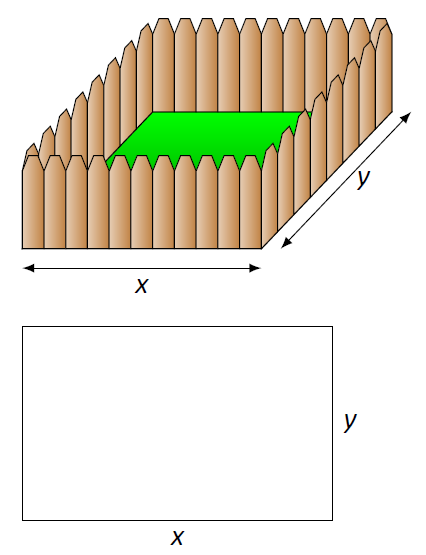
Малюнок$\PageIndex{1}$: Ескіз вольєра в прикладі$\PageIndex{1}$.

Допускаємо$x$ і$y$ позначаємо довжини сторін прямокутника. Зрозуміло,

\[\text{Area}=xy.\]

Ми ще не знаємо, як обробляти функції з 2 змінними; нам потрібно зменшити це до однієї змінної. Ми знаємо більше про ситуацію: чоловік має 100 футів огорожі. Знаючи, що периметр прямокутника повинен бути 100, ми можемо створити ще одне рівняння:

\[\text{Perimeter} = 100 = 2x+2y.\]

Тепер у нас є 2 рівняння і 2 невідомих. В останньому рівнянні вирішуємо для$y$:

\[y = 50-x.\]

Тепер підставляємо цей вираз$y$ в рівняння площі:

\[ \text{Area} = A(x) = x(50-x).\]

Зверніть увагу, що тепер у нас є рівняння однієї змінної; ми дійсно можемо назвати Area функцією$x$.

Ця функція має сенс тільки тоді$0\leq x \leq 50$, коли, інакше ми отримуємо негативні значення площі. Таким чином, ми знаходимо крайні значення$A(x)$ на інтервалі$[0,50]$.

Щоб знайти критичні точки, беремо похідну від$A(x)$ і ставимо її рівною 0, потім вирішуємо для$x$.

\[\begin{align} A(x) &= x(50-x) \\ &= 50x-x^2 \\ A'(x) &= 50-2x \end{align}\]

Ми вирішуємо$50-2x=0$ знайти$x=25$; це єдина критична точка. Ми оцінюємо$A(x)$ в кінцевих точках нашого інтервалу і в цій критичній точці, щоб знайти крайні значення; в цьому випадку все, що нас хвилює, - це максимум.

Ясно$A(0)=0$ і$A(50)=0$, тоді як$A(25) = 625 \text{ft}^2$. Це максимум. Оскільки ми раніше знайшли$y = 50-x$, ми виявляємо, що також$y$ є$25$. Таким чином, розміри прямокутного вольєра з периметром 100 футів з максимальною площею - квадрат, зі сторонами довжиною 25 футів.

Цей приклад дуже спрощений і трохи надуманий. (Зрештою, більшість людей створюють дизайн, потім купують огорожі для задоволення своїх потреб, а не купують огорожі та планують пізніше.) Але він добре моделює необхідний процес: створіть рівняння, які описують ситуацію, зводять рівняння до однієї змінної, потім знаходять необхідне екстремальне значення.

«У реальному житті» проблеми набагато складніше. Рівняння часто не зводяться до однієї змінної (отже, потрібне багатозмінне числення), і самі рівняння можуть бути важкими для формування. Розуміння принципів тут забезпечить хорошу основу для математики, з якою ви, швидше за все, зіткнетеся пізніше.

Ми окреслимо тут основний процес вирішення цих завдань оптимізації.

Ключова ідея 6: Розв'язування задач оптимізації

Розберіться в проблемі. Чітко визначте, яку кількість потрібно максимізувати або звести до мінімуму. Зробіть ескіз, якщо корисно.
Створюйте рівняння, що відповідають контексту задачі, використовуючи надану інформацію. (Один з них повинен описувати кількість, яку потрібно оптимізувати. Ми будемо називати це фундаментальним рівнянням.)
Якщо фундаментальне рівняння визначає величину, яку потрібно оптимізувати як функцію більше однієї змінної, зведіть її до однієї змінної функції, використовуючи підстановки, отримані з інших рівнянь.
Визначте область цієї функції, маючи на увазі контекст проблеми.
Знайти крайні значення цієї функції на визначеній області.
Визначте значення всіх відповідних величин проблеми.

Ми будемо використовувати Key Idea 6 в різних прикладах.

Приклад$\PageIndex{2}$: {Optimization: perimeter and area

Ось ще одна класична проблема обчислення: жінка має 100 футів огорожі, маленьку собаку та великий двір, який містить потік (який переважно прямий). Вона хоче створити прямокутну огорожу з максимальною площею, яка використовує потік як одну сторону. (Мабуть, її собака не попливе.) Які розміри забезпечують максимальну площу?

Рішення

Ми будемо слідувати крокам, описаним Key Idea 6.

Ми максимізуємо площу. Допоможе ескіз регіону; малюнок$\PageIndex{2}$ дає два ескізи передбачуваної огородженої території. Ключовою особливістю ескізів є визнання того, що одна сторона не огороджена.

$альт$

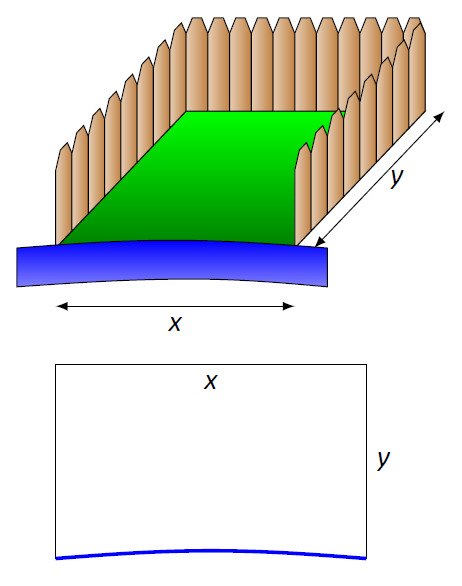
Малюнок$\PageIndex{2}$: Ескіз вольєра в прикладі$\PageIndex{2}$.

Ми хочемо максимізувати площу; як у прикладі раніше, $$\ text {Area} = xy.$$ Це наше фундаментальне рівняння. Це визначає область як функцію двох змінних, тому нам потрібно інше рівняння, щоб зменшити її до однієї змінної.
Ми знову звертаємося до периметра; тут периметр $$\ text {Perimeter} = 100 = x+2y.$$ Зверніть увагу, чим це відрізняється від нашого попереднього прикладу.
Тепер ми зведемо фундаментальне рівняння до однієї змінної. У рівнянні периметра вирішуйте для$y$:$y = 50 - x/2$. Тепер ми можемо написати Площа як $\ text {Площа} = A (x) = x (50-x/2) = 50x -\ frac12x^2.$$ Площа тепер визначається як функція однієї змінної.
Ми хочемо, щоб область була ненегативною. Так як$A(x) = x(50-x/2)$, хочемо$x\geq 0$ і$50-x/2\geq 0$. Остання нерівність означає$x\leq100$, що, так$0\leq x\leq 100$.
Тепер знаходимо крайні значення. У кінцевих точках знаходить мінімум, що дає площу 0.
Знайдіть критичні точки. У нас є$A'(x) = 50-x$; встановивши це рівне 0 і рішення для$x$ повернень$x=50$. Це дає площу $A (50) = 50 (25) = 1250. $$
Ми раніше встановили$y = 50-x/2$; таким чином$y = 25$. Таким чином, наш прямокутник матиме дві сторони довжиною 25 і одну сторону довжиною 50, загальною площею 1250 футів$^2$.

Майте на увазі, коли ми робимо ці проблеми, що ми практикуємо процес; тобто ми вчимося перетворювати ситуацію на систему рівнянь. Ці рівняння дозволяють записати певну величину як функцію однієї змінної, яку ми потім оптимізуємо.

Приклад$\PageIndex{3}$: Optimization: minimizing cost

Лінія електропередач повинна бути прокладена від електростанції, розташованої на пляжі, до офшорного об'єкта. $\PageIndex{3}$На малюнку показані відстані між електростанцією до об'єкта.

Це коштує 50 доларів на фут., щоб запустити лінію електропередач уздовж землі, і 130 доларів за фут., щоб запустити лінію електропередач під водою. Скільки лінії електропередач повинна бути прокладена уздовж землі, щоб мінімізувати загальну вартість? Яка мінімальна вартість?

$альт$

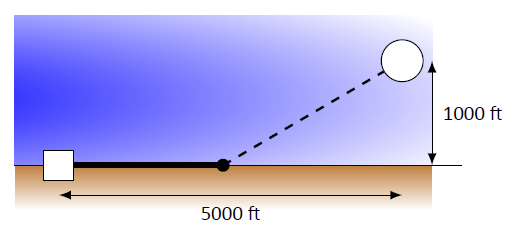
Малюнок$\PageIndex{3}$: Проведення лінії електропередач від електростанції до офшорного об'єкта з мінімальними витратами на прикладі$\PageIndex{3}$

Рішення

Ми будемо слідувати стратегії Key Idea 6 неявно, без конкретної нумерації кроків.

Є два негайних рішення, які ми могли б розглянути, кожне з яких ми відкинемо через «здоровий глузд». По-перше, ми могли б мінімізувати відстань, безпосередньо з'єднавши два місця прямою лінією. Однак для цього потрібно, щоб весь провід був прокладений під водою, найбільш витратний варіант. По-друге, ми могли б мінімізувати підводну довжину, провівши провід на всі 5000 футів вздовж пляжу, безпосередньо навпроти офшорного об'єкта. Це має небажаний ефект від найдовшої відстані з усіх, ймовірно, забезпечуючи немінімальні витрати.

Оптимальне рішення, ймовірно, має лінію, яка проходить уздовж землі деякий час, потім під водою, як випливає з малюнка. Нам потрібно позначити наші невідомі відстані — відстань пробігти уздовж землі і відстань пробігти під водою. Визнаючи, що підводну відстань можна виміряти як гіпотенузу прямокутного трикутника, ми вирішили позначити відстані, як показано на малюнку$\PageIndex{4}$.

$альт$

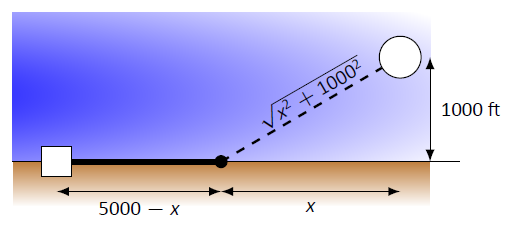
Малюнок$\PageIndex{4}$: Позначення невідомих відстаней у прикладі$\PageIndex{3}$.

Вибираючи так,$x$ як ми зробили, ми робимо вираз під квадратним коренем простим. Тепер ми створюємо функцію витрат.

$
\ begin {масив} {ccccc}
\ текст {Вартість} &= &\ текст {вартість землі} &+ &\ текст {вартість води}\\
& &\ текст {\ $50}\ раз\ текст {відстань землі} &+&\ text {\ $130}\ час\ текст {відстань води}\\
& 50 (5000-x) &+& 130\ sqrt {x ^2+ 1000^2}. \\
\ end {масив}
\]

Отже, ми маємо$c(x) = 50(5000-x)+ 130\sqrt{x^2+1000^2}$. Ця функція має сенс лише на інтервалі$[0,5000]$. Хоча ми досить впевнені, що кінцеві точки не дадуть мінімальних витрат, ми все одно оцінюємо$c(x)$ на кожному для перевірки.

$ $ c (0) = 380,000\ квадратний\ квадратний c (5000)\ приблизно 662,873.\]

Тепер знаходимо критичні значення$c(x)$. Обчислюємо$c'(x)$ як

$ с' (х) = -50+\ розрив {130x} {\ sqrt {x^2+1000^2}}.\]

Визнайте, що це ніколи не визначено. Встановлюючи$c'(x)=0$ і вирішуючи для$x$, ми маємо:

\[ \begin{align} -50+\frac{130x}{\sqrt{x^2+1000^2}} &= 0 \\ \frac{130x}{\sqrt{x^2+1000^2}} &= 50\\ \frac{130^2x^2}{x^2+1000^2} &= 50^2\\ 130^2x^2 &= 50^2(x^2+1000^2) \\ 130^2x^2-50^2x^2 &= 50^2\cdot1000^2\\ (130^2-50^2)x^2 &= 50,000^2\\ x^2 &= \frac{50,000^2}{130^2-50^2}\\ x &= \frac{50,000}{\sqrt{130^2-50^2}}\\ x & = \frac{50,000}{120} =416\frac23\approx 416.67. \end{align}\]

Оцінка$c(x)$ при$x=416.67$ дає вартість близько 370 000 доларів. Відстань, яку лінія електропередач прокладена уздовж землі, становить$5000-416.67 = 4583.33$ фути., а підводна відстань -$\sqrt{416.67^2+1000^2} \approx 1083$ фути.

У вправах ви побачите різноманітні ситуації, які вимагають від вас поєднання навичок вирішення проблем з обчисленням. Зосередьтеся на процесі; дізнайтеся, як формувати рівняння з ситуацій, якими можна маніпулювати в те, що вам потрібно. Уникайте запам'ятовування, як робити «подібну проблему» на відміну від «такого роду проблеми». Навчання процесу принесе користь набагато довше, ніж запам'ятовування певної техніки.

Наступний розділ представляє наше остаточне застосування похідної: диференціали. З огляду на$y=f(x)$, вони пропонують метод наближення зміни$y$ після$x$ змін на невелику суму.