4.4: Диференціали

Last updated
Save as PDF

Page ID: 60671

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У розділі 2.2 ми досліджували значення та використання похідної. Цей розділ починається з перегляду деяких з цих ідей.

Нагадаємо, що похідна функції$f$ може бути використана для знаходження нахилів ліній, дотичних до графіка$f$. В$x=c$, дотична лінія до графіка$f$ має рівняння

$ $ у = ф '(c) (х-с) +f (c).\]

Дотична лінія може бути використана для пошуку хороших наближень$f(x)$ значень$x$ near$c$.

Наприклад, ми можемо наблизити$\sin 1.1$ за допомогою дотичної лінії до графіка$f(x)=\sin x$ в$x=\pi/3 \approx 1.05.$ Відкликати$\sin (\pi/3) = \sqrt{3}/2 \approx 0.866$, що, і$\cos (\pi/3) = 1/2$. Таким чином, дотична лінія до$f(x) = \sin x$ at$x=\pi/3$ дорівнює:

$\ ell (x) =\ фрак12 (х-\ пі/3) +0,866.\]

$альт$ $альт$

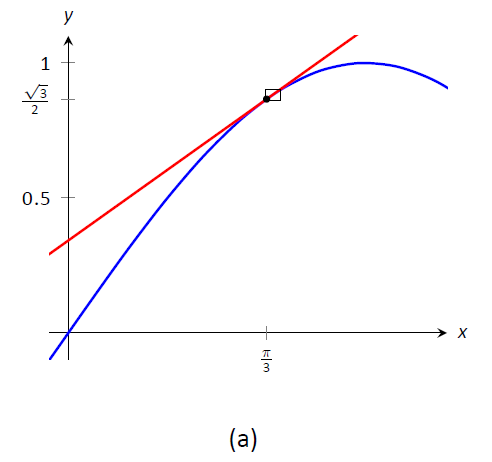
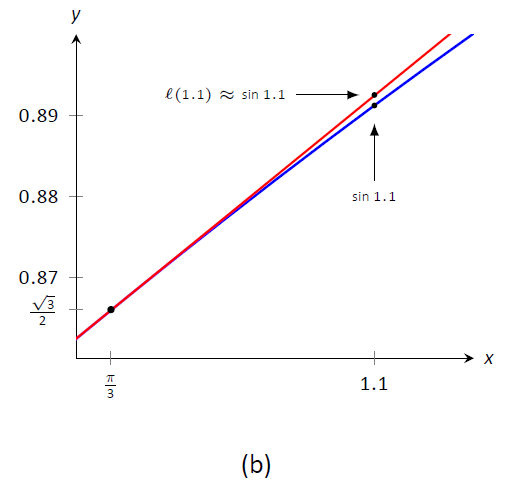
Малюнок$\PageIndex{1}$: Графік$f(x) = \sin x$ і його дотична лінія$x=\pi/3$ в для оцінки$\sin 1.1$.

На$\PageIndex{1a}$ малюнку ми бачимо$f(x) = \sin x$ графічний графік разом з його дотичною лінією в$x=\pi/3$. Маленький прямокутник показує область, яка відображається на малюнку$\PageIndex{1b}$. На цьому малюнку ми бачимо, як ми наближаємося$\sin 1.1$ з дотичною лінією, оцінюваної при$1.1$. Разом ці дві цифри показують, наскільки близькі ці значення.

Використовуючи цей рядок для$\sin 1.1$ наближення, ми маємо:

\[ \begin{align} \ell(1.1) &= \frac12(1.1-\pi/3)+0.866 \\ &= \frac12(0.053)+0.866 = 0.8925. \end{align}\]

(Ми залишаємо це читачеві, щоб побачити, наскільки це добре наближення.)

Ми зараз узагальнюємо це поняття. Задано$f(x)$ та$x$ значення —value$c$, дотична лінія дорівнює$\ell(x) = f'(c)(x-c)+f(c)$. Зрозуміло,$f(c) = \ell(c)$. $\Delta x$Дозволяти невелике число, що представляє собою невелику зміну$x$ вартості. Ми стверджуємо, що:

$ $f (с+\ дельта х)\ приблизно\ ell (с+\ дельта х),\]

оскільки дотична лінія до функції добре наближається до значень цієї функції поблизу$x=c$.

У міру зміни$x$ значення від$c$ до$c+\Delta x$$y$ значення$f$ змінюється від$f(c)$ до$f(c+\Delta x)$. Ми називаємо це зміною$y$ вартості$\Delta y$. Тобто:

$$\ Дельта y = f (с+\ Дельта х) -f (c).\]

$f(c+\Delta x)$Замінюючи його дотичною лінією наближення, ми маємо

\[ \begin{align} \Delta y &\approx \ell(c+\Delta x) - f(c) \notag\\ &= f'(c)\big((c+\Delta x)-c\big)+f(c) - f(c)\notag \\ &=f'(c)\Delta x \end{align}\]

Це остаточне рівняння є важливим; ми повернемося до нього в Key Idea 7.

Введемо дві нові змінні,$dx$ причому$dy$ в контексті формального визначення.

Визначення: Диференціали$x$ and $y$.

Дозвольте$y=f(x)$ бути диференційованим. Диференціал$x$, позначається$dx$, є будь-яким ненульовим дійсним числом (зазвичай прийнято мале число). Диференціал$y$, позначається$dy$, є

\[dy = f'(x)dx.\]

Ми можемо вирішити для$f'(x)$ у наведеному вище рівнянні:$f'(x) = dy/dx$. Це стверджує, що похідна щодо$x$ є$f$ диференціалом$y$ розділеного на диференціал$x$; це не альтернативне позначення для похідної,$\frac{dy}{dx}$. Це останнє позначення було обрано через дробові якості похідної, але знову ж таки, це один символ, а не дріб.

Корисно організувати наші нові концепції та позначення в одному місці.

Ключова ідея 7: Диференціальні позначення

$y = f(x)$Дозволяти диференційовану функцію.

$\Delta x$являє собою невелику ненульову зміну$x$ значення.
$dx$являє собою невелику ненульову зміну$x$ значення (тобто$\Delta x = dx$).
$\Delta y$це зміна$y$ значення як$x$ зміни на$\Delta x$; отже $$\ Delta y = f (x+\ Delta x) -f (x) . $$
$dy = f'(x)dx$який, за рівнянням$\PageIndex{7}$, є наближенням зміни$y$ значення як$x$ зміни на$\Delta x$;$dy \approx \Delta y$.

Яке значення диференціалів? Як і багато математичні поняття, диференціали забезпечують як практичну, так і теоретичну користь. Ми досліджуємо обидва тут.

Приклад$\PageIndex{1}$: Finding and using differentials

Розглянемо$f(x) = x^2$. Знаючи$f(3) = 9$, приблизні$f(3.1)$.

Рішення

$x$Значення змінюється від$x=3$ до$x=3.1$; тому ми це бачимо$dx=0.1$. Якщо ми знаємо, наскільки змінюється$y$ значення від$f(3)$ до$f(3.1)$ (тобто, якщо ми знаємо$\Delta y$), ми будемо точно знати, що$f(3.1)$ таке (оскільки ми вже знаємо$f(3)$). Ми можемо наблизити\ Delta y\ с$dy$.

\[ \begin{align} \Delta y &\approx dy \\ &= f'(3)dx \\ &= 2\cdot 3\cdot 0.1 = 0.6. \end{align}\]

Ми очікуємо, що$y$ значення зміниться приблизно$0.6$, тому ми наближаємо$f(3.1) \approx 9.6.$

Ми залишаємо це читачеві, щоб перевірити це, але попереднє обговорення пов'язує диференціал з дотичною лінією$f(x)$ at$x=3$. Можна перевірити, що дотична лінія, оцінена на$x=3.1$, також дає$y=9.6$.

Звичайно, легко обчислити фактичну відповідь (вручну або за допомогою калькулятора):$3.1^2 = 9.61.$ (Перш ніж ми станемо занадто цинічними і скажемо «Тоді навіщо морочитися?» , Зверніть увагу, наше наближення дійсно добре!)

Так навіщо морочитися?

У «більшості» реальних життєвих ситуацій ми не знаємо функції, яка описує ту чи іншу поведінку. Натомість ми можемо лише проводити вимірювання того, як все змінюється — вимірювання похідної.

Уявіть собі, що вода стікає по звивистому каналу. Легко виміряти швидкість і напрямок (тобто швидкість) води в будь-якому місці. Дуже важко створити функцію, яка описує загальний потік, тому важко передбачити, де опиниться плаваючий об'єкт, розміщений на початку каналу. Однак ми можемо наблизити шлях об'єкта за допомогою диференціалів. За невеликі проміжки часу шлях, прийнятий плаваючим об'єктом, по суті, лінійний. Диференціали дозволяють нам наблизити істинний шлях, об'єднавши багато коротких, лінійних шляхів. Ця методика називається методом Ейлера, вивчається на вступних курсах диференціальних рівнянь.

Ми використовуємо диференціали ще раз, щоб наблизити значення функції. Незважаючи на те, що калькулятори дуже доступні, це акуратно, щоб побачити, як ці методи іноді можуть бути використані, щоб легко обчислити щось, що виглядає досить важко.

Приклад$\PageIndex{2}$: Using differentials to approximate a function value

Приблизний$\sqrt{4.5}$.

Рішення

Ми очікуємо$\sqrt{4.5} \approx 2$, але можемо зробити краще. Нехай$f(x) = \sqrt{x}$, і нехай$c=4$. Таким чином$f(4) = 2$. Ми можемо обчислити$f'(x) = 1/(2\sqrt{x})$, так$f'(4) = 1/4$.

Ми наближаємо різницю між$f(4.5)$ і$f(4)$ використанням диференціалів, з$dx = 0.5$:

$ $ f (4.5) -f (4) =\ Дельта у\ приблизно ди = f '(4)\ cdot x = 1/4\ cdot 1/2 = 1/8 = 0,125.\]

Приблизна зміна$f$ від$x=4$ до$x=4.5$ є$0.125$, тому ми наближаємо$\sqrt{4.5} \approx 2.125.$

Диференціали важливі, коли ми обговорюємо інтеграцію. Коли ми вивчаємо цю тему, ми будемо використовувати такі позначення, як

$\ int ф (х)\ дх\]

досить часто. Хоча ми не обговорюємо тут, що все це означає позначення, зверніть увагу на існування диференціала$dx$. Правильне поводження з інтегралами поставляється з правильною обробкою диференціалів.

Зважаючи на це, ми практикуємо пошук диференціалів загалом.

Приклад$\PageIndex{3}$: Finding differentials

У кожному з наступних знайдіть диференціал$dy$.

\[y = \sin x \qquad\quad 2. y = e^x(x^2+2) \quad\qquad 3. y = \sqrt{x^2+3x-1}\]

S рішення

$y = \sin x$: Як$f(x) = \sin x$,$f'(x) = \cos x$. Таким чином $ $ dy =\ cos (х) дх. $$
$y = e^x(x^2+2)$: Нехай$f(x) = e^x(x^2+2)$. Нам потрібно$f'(x)$, вимагаючи Правило продукту.
У нас є$f'(x) = e^x(x^2+2) + 2xe^x$, так $dy =\ великий (е ^ х (х ^ 2+2) + 2xe ^ х\ великий) ДХ. $$
$y = \sqrt{x^2+3x-1}$: Нехай$f(x) = \sqrt{x^2+3x-1}$; нам потрібно$f'(x)$, вимагаючи Правило ланцюга.
У нас є$\Delta s f'(x) = \frac{1}{2}(x^2+3x-1)^{-\frac12}(2x+3) = \frac{2x+3}{2\sqrt{x^2+3x-1}}.$ Таким чином $dy =\ розриву {(2x+3) х} {2\ sqrt {x^2+3x-1}} . $$

Знайти диференціал$dy$$y=f(x)$ насправді не складніше, ніж знайти похідну$f$; ми просто множимо$f'(x)$ на$dx$. Важливо пам'ятати, що ми не просто додаємо символ "$dx$" в кінці.

Ми бачили практичне використання диференціалів, оскільки вони пропонують хороший метод прийняття певних наближень. Інше використання - поширення помилок. Припустимо, довжина вимірюється бути$x$, хоча фактичне значення є$x+\Delta x$ (де ми сподіваємося\ Delta x\ мало). Це вимірювання$x$ може бути використано для обчислення деякого іншого значення; ми можемо думати про це як$f(x)$ для якоїсь функції$f$. Як справжня довжина$x+\Delta x$, один дійсно повинен був обчислити$f(x+\Delta x)$. Різниця між$f(x)$ і$f(x+\Delta x)$ є поширеною помилкою.

Наскільки близькі$f(x)$ і$f(x+\Delta x)$? Це різниця значень «y»;

$f (x+\ Дельта х) -f (x) =\ Дельта у\ приблизно день.\]

Ми можемо наблизити поширену помилку за допомогою диференціалів.

Приклад$\PageIndex{4}$: Using differentials to approximate propagated error

Сталевий кульковий підшипник повинен бути виготовлений діаметром 2 см. Процес виготовлення має допуск в$\pm 0.1$ мм в діаметрі. З огляду на, що щільність стали становить близько 7,85 г/см$^3$, оцініть поширену похибку в масі кульової опори.

Рішення

Масу кулькового підшипника знаходять за допомогою рівняння «маса = об'ємна$\times$ щільність». У цій ситуації масова функція є добутком радіуса кулькового підшипника, отже, вона є$m = 7.85\frac43\pi r^3$. Диференціал маси дорівнює

$ дм = 31.4\ пі р^2 д-р.\]

Радіус повинен бути 1см; виробничий допуск в радіусі -$\pm 0.05$ мм, або$\pm 0.005$ см. Поширення помилки приблизно:

\[\begin{align} \Delta m & \approx dm \\ &= 31.4\pi (1)^2 (\pm 0.005) \\ &= \pm 0.493\text{g} \end{align}\]

Чи значна ця помилка? Це, безумовно, залежить від програми, але ми можемо отримати уявлення, обчисливши відносну помилку. Співвідношення між величиною похибки до загальної маси дорівнює

\[\begin{align} \frac{dm}{m} &= \pm \frac{0.493}{7.85\frac43\pi} \\ &=\pm \frac{0.493}{32.88}\\ &=\pm 0.015,\end{align}\]

або$\pm 1.5$.

Ми залишаємо це читачеві, щоб підтвердити це, але якщо діаметр кулі повинен був бути 10см, той же виробничий допуск дасть поширену похибку в масі$\pm12.33$ g, яка відповідає\ textit {percent error}$\pm0.188$\%. Хоча сума помилки набагато більша ($12.33> 0.493$), відсоток похибки набагато нижчий.

Вперше ми дізналися про похідну в контексті миттєвих швидкостей зміни та нахилів дотичних ліній. Ми сприяли нашому розумінню сили похідної, вивчивши, як вона пов'язана з графіком функції (що призводить до ідей збільшення/зменшення та увігнутості). Ця глава поставила похідну до ще більшого використання:

Розв'язування рівнянь (метод Ньютона)
Пов'язані тарифи (подальше використання похідної для пошуку миттєвих темпів зміни)
Оптимізація (застосовані екстремальні значення), і
Диференціали (корисні для різних наближень і для чогось, званого інтеграцією).

У наступних розділах ми розглянемо «зворотну» задачу до обчислення похідної: якщо задати функцію$f$, чи можна знайти функцію, похідна якої є$f$? Вміти зробити це відкриває неймовірний світ математики та додатків.