4.2: Супутні тарифи

Last updated
Save as PDF

Page ID: 60678

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Коли дві величини пов'язані рівнянням, знаючи значення однієї величини можна визначити значення іншої. Наприклад, окружність і радіус кола пов'язані між собою$C=2\pi r$; знаючи, що$C = 6\pi$ в визначає радіус повинен бути 3 дюйма.

Тема пов'язаних ставок робить цей крок далі: знаючи швидкість, з якою змінюється одна кількість, може визначити швидкість, з якою змінюється інша.

Примітка. Цей розділ значною мірою спирається на неявну диференціацію, тому повернення до розділу 2.6 може допомогти. Ми демонструємо поняття пов'язаних ставок на прикладах.

Приклад$\PageIndex{1}$: Understanding related rates

Радіус кола зростає зі швидкістю 5 в/год. З якою швидкістю зростає окружність?

Рішення

Окружність і радіус кола пов'язані між собою$C = 2\pi r$. Нам дають інформацію про те, яка тривалість$r$ змін щодо часу; тобто нам говорять$\frac{dr}{dt} = 5$ в/ч. Ми хочемо знати, як тривалість$C$ змін щодо часу, тобто ми хочемо знати$\frac{dC}{dt}$.

Неявно диференціювати обидві сторони щодо$t$:$C = 2\pi r$

\ [\ почати {вирівнювати*} C &= 2\ пі r\\\ розриву {d} {dt}\ великий (C\ великий) &=\ розриву {d} {dt}\ великий (2\ пі р\ великий)\\\ розрив {dC} {dt} &= 2\ pi\ frac {dt} {dt} {dt}.
\ end {вирівнювати*}\]

Як ми знаємо$\frac{dr}{dt} = 5$ в/год, ми знаємо

$\ розрив {dC} {dT} = 2\ пі 5 = 10\ пі\ приблизно 31,4\ текст {в/год.}\]

Розглянемо інший, схожий приклад.

Приклад$\PageIndex{2}$: Finding related rates

Вода витікає з крана зі швидкістю$^3$ в/с на рівну поверхню з постійною швидкістю, утворюючи кругову калюжу, яка знаходиться$1/8$ в глибині.$2$

З якою швидкістю зростає площа калюжі?
З якою швидкістю зростає радіус кола?

Рішення

1. Відповісти на це питання можна двома способами: використовуючи «здоровий глузд» або пов'язані з ними тарифи. Метод здорового глузду стверджує, що обсяг калюжі зростає$2$ на$^3$ в/с, де

\[\text{volume of puddle}\, =\, \text{area of circle} \times \text{depth}.\]

Оскільки глибина постійна$1/8$ в, площа повинна зростати на 16in$^2$ /с.

Цей підхід розкриває базовий принцип споріднених ставок. $V$$A$Дозволяти і представляти обсяг і площа калюжі. Ми знаємо$V= A\times \frac18$. Візьміть похідну обох сторін щодо$t$, використовуючи неявну диференціацію.

\[\begin{align} V &= \frac18A\\ \frac{d}{dt}\big(V\big) &= \frac{d}{dt}\left(\frac18A\right)\\ \frac{dV}{dt} &= \frac18\frac{dA}{dt} \end{align}\]

Як$\frac{dV}{dt} = 2$, ми знаємо$2 = \frac18\frac{dA}{dt}$, а значить$\frac{dA}{dt} = 16$. Таким чином, площа зростає на 16в$^2$ /с.

2. Для початку нам потрібно рівняння, яке пов'язує те, що ми знаємо, з радіусом. Ми щойно дізналися щось про площу поверхні кругової калюжі, і ми знаємо$A = \pi r^2$. Ми повинні мати можливість дізнатися про швидкість, з якою радіус зростає за допомогою цієї інформації.

Неявно вивести обидві сторони щодо$t$:$A=\pi r^2$

\[\begin{align} A &= \pi r^2 \\ \frac{d}{dt}\big(A\big) &= \frac{d}{dt}\big(\pi r^2\big)\\ \frac{dA}{dt} &= 2\pi r\frac{dr}{dt} \end{align}\]

Наша робота вище розповіла нам, що$\frac{dA}{dt} = 16\text{in}^2$ /s. рішення для$\frac{dr}{dt}$, у нас є

$\ frac {dr} {dt} =\ frac {8} {\ pi r}.\]

Зверніть увагу, як наша відповідь не є числом, а скоріше функцією$r$. Іншими словами, швидкість, з якою радіус зростає, залежить від того, наскільки велике коло вже є. Якщо коло дуже велике, додавання 2в$^3$ води зовсім не зробить коло набагато більше. Якщо коло розміром з копійки, додавання такої ж кількості води призведе до радикальної зміни радіуса кола.

У чомусь наша проблема була (навмисно) погано поставлена. Нам потрібно вказати радіус струму, щоб знати швидкість зміни. Коли калюжа має радіус 10in, радіус зростає зі швидкістю

$\ розрив {dr} {dt} =\ frac {8} {10\ pi} =\ frac {4} {5\ pi}\ приблизно 0,25\ текст {в/с}.\]

Приклад$\PageIndex{3}$: Studying related rates

Радіолокаційні гармати вимірюють швидкість зміни відстані між гарматою і об'єктом, який вона вимірює. Наприклад, читання «55 миль/год» означає, що об'єкт віддаляється від пістолета зі швидкістю 55 миль на годину, тоді як вимірювання «$-25$миль/год» означало б, що об'єкт наближається до пістолета зі швидкістю 25 миль на годину.

Якщо радіолокаційна гармата рухається (скажімо, прикріплена до поліцейської машини), то радіолокаційні показання зрозумілі лише відразу, якщо пістолет і об'єкт рухаються по одній лінії. Якщо поліцейський подорожує 60 миль/год і отримує показання 15mph, він знає, що автомобіль попереду нього рухається зі швидкістю 15 миль на годину, тобто автомобіль їде 75 км/год. (Цей принцип прямої лінії є однією з причин, чому офіцери паркуються на узбіччі шосе і намагаються стріляти прямо вниз по дорозі. Це дає найбільш точне читання.)

Припустимо, офіцер їде через північ зі швидкістю 30 миль/год і бачить автомобіль, що рухається на схід, як показано на малюнку$\PageIndex{1}$. Використовуючи свій радіолокаційний пістолет, він вимірює показання 20 миль/год. Використовуючи орієнтири, він вважає, що і він, і інший автомобіль знаходяться приблизно в 1/2 милі від перетину їх двох доріг.

$альт$

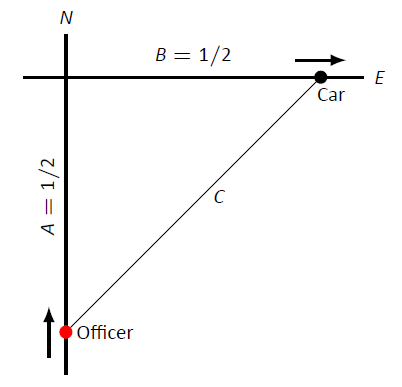
Малюнок$\PageIndex{1}$: Ескіз поліцейської машини (внизу), яка намагається виміряти швидкість автомобіля (праворуч) у прикладі$\PageIndex{3}$.

Якщо обмеження швидкості на іншій дорозі становить 55 км/год, чи інший водій перевищує швидкість?

Рішення

Використовуючи діаграму на малюнку$\PageIndex{1}$, давайте позначимо те, що нам відомо про ситуацію. Оскільки і поліцейський, і інший водій знаходяться в 1/2 милі від перехрестя$A = 1/2$$B = 1/2$, ми маємо, і через теорему Піфагора,$C = 1/\sqrt{2}\approx 0.707$.

Ми знаємо, що поліцейський їде зі швидкістю 30 миль/год; тобто$\frac{dA}{dt} = -30$. Причиною цього темпу змін є негативним,$A$ є те, що стає менше; відстань між офіцером і перехрестям скорочується. Радіолокаційне вимірювання є$\frac{dC}{dt} = 20$. Ми хочемо знайти$\frac{dB}{dt}$.

Нам потрібно рівняння, яке відноситься$B$ до$A$ і/або$C$. Теорема Піфагора - хороший вибір:$A^2+B^2 = C^2$. Диференціювати обидві сторони щодо$t$:

\[\begin{align} A^2 + B^2 &= C^2 \\ \frac{d}{dt}\left(A^2+B^2\right) &= \frac{d}{dt}\left(C^2\right) \\ 2A\frac{dA}{dt} + 2B\frac{dB}{dt} &= 2C\frac{dC}{dt} \end{align} \]

У нас є цінності для всього, крім$\frac{dB}{dt}$. Рішення для цього у нас є

$\ розрив {дБ} {dT} =\ гідророзриву {C\ frac {dC} {dT} - A\ frac {dT} {dt}} {B}\ приблизно 58.28\ текст {mph}.\]

Інший водій, здається, трохи перевищує швидкість.

Примітка: Приклад$\PageIndex{3}$ є одночасно цікавим і непрактичним. Він підкреслює складність використання радара нелінійним способом і пояснює, чому «в реальному житті» поліцейський слідував за іншим водієм, щоб визначити свою швидкість, а не витягувати олівець і папір.

Принципи тут важливі, хоча. Багато автоматизовані транспортні засоби роблять судження про інші рухомі об'єкти на основі сприйнятих відстаней, радіолокаційних вимірювань та концепцій пов'язаних ставок.

Приклад$\PageIndex{4}$: Studying related rates

Камера розміщена на штативі 10 футів від узбіччя дороги. Камера повинна повернути, щоб відстежувати автомобіль, який повинен проїхати зі швидкістю 100 км/год для рекламного відео. Планувальники відео хочуть знати, яким двигуном повинен бути оснащений штатив, щоб правильно відстежувати автомобіль, коли він проходить повз. На малюнку$\PageIndex{2}$ показана запропонована настройка.

$альт$

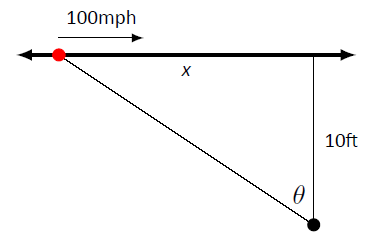
Малюнок$\PageIndex{2}$: Відстеження автомобіля, що перевищує швидкість (зліва) з обертається камерою.

Як швидко камера повинна бути в змозі повернути, щоб відстежувати автомобіль?

Рішення

Ми шукаємо інформацію про те, наскільки швидко камера повертається; отже, нам потрібно рівняння, яке буде$\theta$ співвідносити кут до положення камери та швидкості та положення автомобіля.

Малюнок$\PageIndex{2}$ пропонує використовувати тригонометричне рівняння. Дозволяючи$x$ представляти відстань автомобіля від точки на дорозі безпосередньо перед камерою, ми маємо

\[ \tan \theta = \frac{x}{10}\]

Оскільки автомобіль рухається зі швидкістю 100 км/год, у нас є$\frac{dx}{dt} = -100$ миль/год (як в останньому прикладі,$x$ оскільки стає менше, коли автомобіль подорожує,$\frac{dx}{dt}$ є негативним). Нам потрібно перетворити вимірювання, щоб вони використовували однакові одиниці; перепишіть -100mph з точки зору ft/s:

$\ розрив {dx} {dt} = -100\ розрив {\ текст {м}} {\ текст {hr}} = -100\ розрив {\ текст {м}} {\ текст {hr}}\ cdot5280\ frac {\ текст {ft}} {\ текст {м}}\ cdot\ frac {1} {3600} hr}} {\ текст {s}} =-146. \ оверлайн {6}\ текст {ft/s}.\]

Тепер візьмемо похідну обох сторін рівняння,$\PageIndex{9}$ використовуючи неявну диференціацію:

\[\begin{align} \tan \theta &= \frac{x}{10} \\ \frac{d}{dt}\big(\tan \theta\big) &= \frac{d}{dt}\left(\frac{x}{10}\right) \\ \sec^2\theta\,\frac{d\theta}{dt} &= \frac{1}{10}\frac{dx}{dt}\\ \frac{d\theta}{dt} &= \frac{\cos^2\theta}{10}\frac{dx}{dt} \end{align}\]

Ми хочемо знати, що найшвидше камера повинна повернути. Здоровий глузд говорить нам, що це коли автомобіль знаходиться безпосередньо перед камерою (тобто коли$\theta = 0$). Наша математика несе це. У Рівнянні$\PageIndex{14}$ ми бачимо,$\cos^2\theta$ що це коли найбільший; це коли$\cos \theta = 1$ чи коли$\theta = 0$.

З$\frac{dx}{dt} \approx -146.67$ ft/s ми маємо

$\ frac {d\ тета} {dt} = -\ frac {1\ текст {rad}} {10\ текст {ft}} 146.67\ текст {ft/s} = -14.667\ текст {радіан/с}.\]

Ми знаходимо, що$\frac{d\theta}{dt}$ є негативним; це відповідає нашій діаграмі$\PageIndex{2}$ на малюнку для$\theta$ стає менше, коли автомобіль наближається до камери.

Яке практичне значення$-14.667$ радіанів/с? Нагадаємо, що 1 круговий оборот йде через$2\pi$ радіани, таким чином$14.667$ rad/s означає$14.667/(2\pi)\approx 2.33$ обороти в секунду. Негативний знак вказує на те, що камера обертається за годинниковою стрілкою.

Введено похідну як функцію, яка дає нахили дотичних ліній функцій. У цій главі підкреслюється використання похідної іншими способами. Метод Ньютона використовує похідну для наближення коренів функцій; цей розділ підкреслює аспект «швидкості зміни» похідної, щоб знайти зв'язок між швидкостями зміни двох пов'язаних величин. У наступному розділі ми використовуємо поняття Extreme Value для оптимізації величин.