3.4: Швидкість зміни та поведінка графіків

Last updated
Save as PDF

Page ID: 59649

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Знайти середню швидкість зміни функції.
Використовуйте графік, щоб визначити, де функція збільшується, зменшується або константа.
Використовуйте графік, щоб знайти локальні максимуми та локальні мінімуми.
Використовуйте графік, щоб знайти абсолютний максимум і абсолютний мінімум.

Витрати на бензин зазнали деяких диких коливань за останні кілька десятиліть. У таблиці$\PageIndex{1}$ наведено середню вартість, в доларах, галона бензину за 2005—2012 роки. Вартість бензину можна розглядати як функцію року.

Таблиця$\PageIndex{1}$
$y$	2005	2006	2007	2008	2009	2010	2011	2012
$C(y)$	2.31	2.62	2.84	3.30	2.41	2.84	3.58	3.68

Якби нас цікавило лише те, як змінювалися ціни на бензин між 2005 та 2012 роками, ми могли б обчислити, що вартість за галон зросла з 2,31 до 3,68 доларів, збільшившись на 1,37 долара. Хоча це цікаво, може бути корисніше подивитися, наскільки змінилася ціна за рік. У цьому розділі ми розглянемо такі зміни, як ці.

Пошук середньої швидкості зміни функції

Зміна ціни на рік - це швидкість зміни, оскільки вона описує, як змінюється кількість випуску відносно зміни вхідної кількості. Ми бачимо, що ціна бензину в$\PageIndex{1}$ табл щороку не змінювалася на однакову суму, тому темпи зміни не були постійними. Якщо ми використовуємо лише початкові та кінцеві дані, ми знаходимо середню швидкість зміни за вказаний проміжок часу. Щоб знайти середню швидкість зміни, ділимо зміна вихідного значення на зміну вхідного значення.

\[\begin{align*} \text{Average rate of change}&=\dfrac{\text{Change in output}}{\text{Change in input}} \\[4pt] &=\dfrac{\Delta y}{\Delta x}\\[4pt] &=\dfrac{y_2-y_1}{x_2-x_1}\\[4pt] &=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\end{align*} \label{1.3.1}\]

Грецька буква$\Delta$ (дельта) означає зміну кількості; ми читаємо співвідношення як «дельта-$y$ над дельта-$x$» або «зміна$y$ розділеного на зміну»$x$. Іноді ми пишемо$\Delta f$ замість$\Delta y$, який як і раніше представляє зміну вихідного значення функції в результаті зміни його вхідного значення. Це не означає, що ми змінюємо функцію на якусь іншу функцію.

У нашому прикладі ціна бензину зросла на $1,37 з 2005 по 2012 рік. За 7 років середній темп змін становив

\[\dfrac{\Delta y}{\Delta x}=\dfrac{$1.37}{7 \text{years}}\approx \text{0.196 dollars per year.} \label{1.3.2}\]

В середньому ціна на газ збільшувалася приблизно на 19,6 центів щороку. Інші приклади темпів змін включають:

Популяція щурів збільшується на 40 щурів на тиждень
Автомобіль, який подорожує 68 миль на годину (пройдена відстань змінюється на 68 миль щогодини з плином часу)
Автомобіль, що рухається 27 миль на галон (пройдена відстань змінюється на 27 миль за кожен галон)
Струм по електричному ланцюгу збільшується на 0,125 ампер на кожен вольт підвищеної напруги
Сума грошей на рахунку коледжу зменшується на $4,000 за квартал

Визначення: Швидкість змін

Швидкість зміни описує, як змінюється вихідна величина відносно зміни вхідної кількості. Одиниці на швидкості зміни є «одиницями виведення на вхідні одиниці».

Середня швидкість зміни між двома вхідними значеннями - це сумарна зміна значень функції (вихідних значень), поділена на зміну вхідних значень.

\[\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\]

Як...

Враховуючи значення функції в різних точках, обчислити середню швидкість зміни функції для інтервалу між двома значеннями$x_1$ і$x_2$.

Обчисліть різницю$y_2−y_1=\Delta y$.
Обчисліть різницю$x_2−x_1=\Delta x$.
Знайдіть співвідношення$\dfrac{\Delta y}{\Delta x}$.

Приклад$\PageIndex{1}$: Computing an Average Rate of Change

Використовуючи дані таблиці$\PageIndex{1}$, знайдіть середню швидкість зміни ціни бензину в період з 2007 по 2009 рік.

Рішення

У 2007 році ціна бензину склала $2,84. У 2009 році вартість склала $2,41. Середня швидкість зміни становить

\[\begin{align*} \dfrac{\Delta y}{\Delta x}&=\dfrac{y_2−y_1}{x_2−x_1} \\[4pt] &=\dfrac{$2.41−$2.84}{2009−2007} \\[4pt] &=\dfrac{−$0.43}{2 \text{ years}} \\[4pt] &=−$0.22 \text{ per year} \end{align*}\]

Аналіз

Відзначимо, що зниження виражається негативною зміною або «негативним збільшенням». Швидкість зміни є негативною, коли вихід зменшується у міру збільшення вхідного сигналу або коли вихід збільшується, коли вхід зменшується.

Вправа$\PageIndex{1}$

Використовуючи дані в таблиці$\PageIndex{1}$, знайдіть середню швидкість зміни між 2005 і 2010 роками.

Рішення: $\dfrac{$2.84−$2.315}{5 \text{ years}} =\dfrac{$0.535}{5 \text{ years}} =$0.106 \text{per year.}$

Приклад$\PageIndex{2}$: Computing Average Rate of Change from a Graph

З огляду на функцію,$g(t)$ показану на малюнку$\PageIndex{1}$, знайдіть середню швидкість зміни на інтервалі$[−1,2]$.

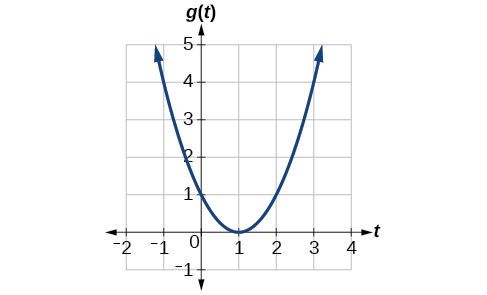
Малюнок$\PageIndex{1}$: Графік параболи.

Рішення

В$t=−1$, на малюнку$\PageIndex{2}$ показано$g(−1)=4$. На$t=2$, графік показує$g(2)=1$.

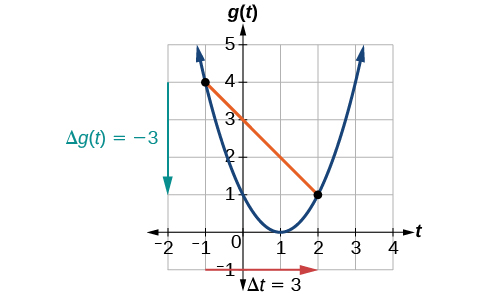
Рисунок$\PageIndex{2}$: Графік параболи з лінією з точок (-1, 4) та (2, 1), щоб показати зміни для g (t) та t.

Горизонтальна зміна$\Delta t=3$ показана червоною стрілкою, а вертикальна зміна$\Delta g(t)=−3$ показана бірюзовою стрілкою. Вихід змінюється на —3, тоді як вхід змінюється на 3, даючи середню швидкість зміни

\[\dfrac{1−4}{2−(−1)}=\dfrac{−3}{3}=−1\]

Аналіз

Зверніть увагу, що замовлення, яке ми вибираємо, дуже важливий. Якщо, наприклад, ми використовуємо$\dfrac{y_2−y_1}{x_1−x_2}$, ми не отримаємо правильної відповіді. Вирішіть, яка точка буде 1, а яка точка буде 2, і збережіть координати фіксованими як$(x_1,y_1)$ і$(x_2,y_2)$.

Приклад$\PageIndex{3}$: Computing Average Rate of Change from a Table

Підібравши друга, який живе за 10 миль, Анна записує свою відстань від дому з плином часу. Значення наведені в табл$\PageIndex{2}$. Знайдіть її середню швидкість за перші 6 годин.

Таблиця$\PageIndex{2}$
$t$(годин)	0	1	2	3	4	5	6	7
$D(t)$(милі)	10	55	90	153	214	240	292	300

Рішення

Тут середня швидкість - це середня швидкість зміни. Вона проїхала 292 милі за 6 годин, за середню швидкість

\[\begin{align*}\dfrac{292−10}{6−0}&=\dfrac{282}{6}\\[4pt] &= 47\end{align*}\]

Середня швидкість - близько 47 миль на годину.

Аналіз

Оскільки швидкість не постійна, середня швидкість залежить від обраного інтервалу. Для інтервалу$[2,3]$ середня швидкість становить 63 милі на годину.

Приклад$\PageIndex{4}$: Computing Average Rate of Change for a Function Expressed as a Formula

Обчислити середню швидкість зміни$f(x)=x^2−\frac{1}{x}$ на інтервалі$[2, 4]$.

Рішення

Ми можемо почати з обчислення значень функцій в кожній кінцевій точці інтервалу.

\[\begin{align*}f(2)&=2^2−\frac{1}{2} f(4)&=4^2−\frac{1}{4} \\[4pt] &=4−\frac{1}{2} &=16−\frac{1}{4} \\[4pt] &=72 &=\frac{63}{4}\end{align*}\]

Тепер обчислюємо середню швидкість зміни.

\[\begin{align*}\text{Average rate of change} &=\dfrac{f(4)−f(2)}{4−2} \\[4pt] &=\dfrac{\frac{63}{4}-\frac{7}{2}}{4-2} \\[4pt] &=\dfrac{\frac{49}{4}}{2} \\[4pt] &= \dfrac{49}{8}\end{align*}\]

Вправа$\PageIndex{2}$

Знайти середню швидкість зміни$f(x)=x−2\sqrt{x}$ на інтервалі$[1, 9]$.

Рішення: $\frac{1}{2}$

Приклад$\PageIndex{5}$: Finding the Average Rate of Change of a Force

Електростатична сила$F$, виміряна в ньютонах, між двома зарядженими частинками може бути пов'язана з відстанню між частинками$d$, в сантиметрах, за формулою$F(d)=\frac{2}{d^2}$. Знайти середню швидкість зміни сили, якщо відстань між частинками збільшено з 2 см до 6 см.

Рішення

Обчислюємо середню швидкість зміни$F(d)=\dfrac{2}{d^2}$ на інтервалі$[2,6]$.

\[\begin{align*}\text{Average rate of change }&=\dfrac{F(6)−F(2)}{6−2} \\[4pt] &=\dfrac{\frac{2}{6^2}-\frac{2}{2^2}}{6-2} & \text{Simplify} \\[4pt] &=\dfrac{\frac{2}{36}-\frac{2}{4}}{4} \\[4pt] &=\dfrac{-\frac{16}{36}}{4} & \text{Combine numerator terms.} \\[4pt] &=−\dfrac{1}{9} & \text{Simplify}\end{align*}\]

Середня швидкість зміни -$−\frac{1}{9}$ ньютон на сантиметр.

Приклад$\PageIndex{6}$: Finding an Average Rate of Change as an Expression

Знайти середню швидкість зміни$g(t)=t^2+3t+1$ на інтервалі$[0, a]$. Відповіддю буде вираз за участю$a$.

Рішення

Використовуємо формулу середньої швидкості зміни.

$\begin{align*}\text{Average rate of change} &=\dfrac{g(a)−g(0)}{a−0} & \text{Evaluate.} \\[4pt] &=\dfrac{(a^2+3a+1)−(0^2+3(0)+1)}{a−0} & \text{Simplify.} \\[4pt] &=\dfrac{a^2+3a+1−1}{a} & \text{Simplify and factor.}\\[4pt] &= \dfrac{a(a+3)}{a} & \text{Divide by the common factor a.}\\[4pt] &= a+3 \end{align*}$

Цей результат говорить нам про середню швидкість зміни з точки зору між$t=0$ та будь-якою іншою точкою$t=a$. Наприклад, на$[0,5]$ інтервалі середня швидкість зміни становила б$5+3=8$.

Вправа$\PageIndex{3}$

Знайти середню швидкість зміни$f(x)=x^2+2x−8$ на інтервалі$[5, a]$.

Рішення: $a+7$

Використання графіка для визначення місця, де функція збільшується, зменшується або константа

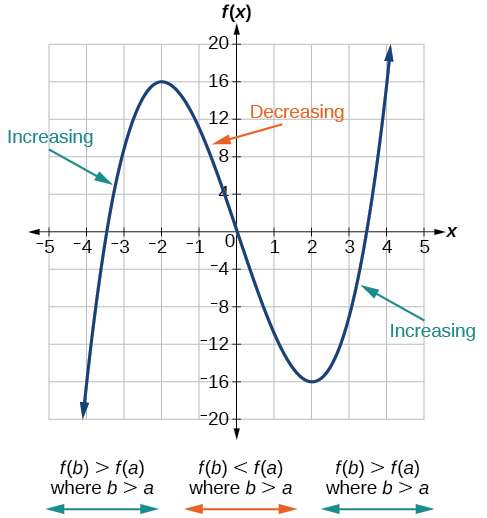
В рамках вивчення того, як змінюються функції, ми можемо визначити інтервали, протягом яких функція змінюється певним чином. Ми говоримо, що функція збільшується на інтервалі, якщо значення функції збільшуються у міру збільшення вхідних значень протягом цього інтервалу. Аналогічно, функція зменшується на інтервалі, якщо значення функції зменшуються у міру збільшення вхідних значень протягом цього інтервалу. Середня швидкість зміни зростаючої функції позитивна, а середня швидкість зміни спадної функції - негативна. $\PageIndex{3}$На малюнку показані приклади збільшення та зменшення інтервалів на функції.

Графік полінома, який показує зростаючі та зменшуються інтервали і локальний максимум і мінімум. — Малюнок$\PageIndex{3}$:$f(x)=x^3−12x$ Функція збільшується$(−\infty, −2)\cup (2,\infty)$ і зменшується$(−2, 2)$.

Хоча деякі функції збільшуються (або зменшуються) над усім своїм доменом, багато інших - ні. Значення вхідних даних, де функція змінюється від збільшення до зменшення (при переході зліва направо, тобто у міру збільшення вхідної змінної) називається локальним максимумом. Якщо функція має більше одного, ми говоримо, що вона має локальні максимуми. Аналогічно, значення вхідних даних, де функція змінюється від зменшення до збільшення у міру збільшення вхідної змінної, називається локальним мінімумом. Форма множини - «локальні мінімуми». Разом локальні максимуми і мінімуми називаються локальними екстремумами, або локальними екстремальними значеннями функції. (Форма однини - «екстремум».) Найчастіше термін місцевий замінюється терміном відносний. У цьому тексті ми будемо використовувати термін локальний.

Зрозуміло, що функція не збільшується і не зменшується на інтервалі, де вона постійна. Функція також не збільшується і не зменшується при крайності. Зауважте, що ми маємо говорити про локальну екстрему, оскільки будь-який заданий локальний екстремум, як визначено тут, не обов'язково є найвищим максимумом або найнижчим мінімумом у всій області функції.

Для функції, графік якої показаний на малюнку$\PageIndex{4}$, локальний максимум дорівнює 16, і відбувається він при$x=−2$. Локальним мінімумом є −16 і відбувається за адресою$x=2$.

Графік многочлена, який показує зростаючі та зменшуються інтервали та локальний максимум.] Визначення локального максимуму — Рисунок$\PageIndex{4}$: Графік многочлена, який показує зростаючі та зменшуються інтервали та локальний максимум.максимальний

Щоб знайти локальні максимуми та мінімуми на графіку, нам потрібно спостерігати за графіком, щоб визначити, де графік досягає своїх найвищих та найнижчих точок відповідно у відкритому інтервалі. Як і вершина американських гірок, графік функції вищий на локальному максимумі, ніж у сусідніх точках з обох сторін. Графік також буде нижчим при локальному мінімумі, ніж в сусідніх точках. Малюнок$\PageIndex{5}$ ілюструє ці ідеї для локального максимуму.

Графік полінома, який показує зростаючі та зменшуються інтервали та локальний максимум. — Малюнок$\PageIndex{5}$: Визначення локального максимуму

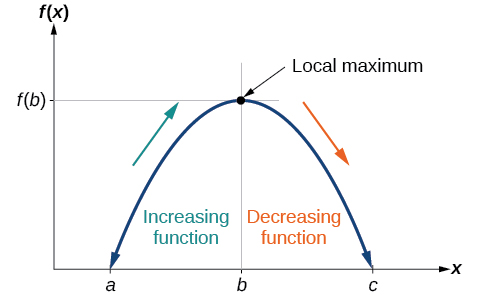
Ці спостереження призводять нас до формального визначення локальних екстрем.

Локальні мінімуми та місцеві максими

Функція$f$ - це зростаюча функція на відкритому інтервалі якщо$f(b)>f(a)$ для кожного$a$,$b$ інтервал де$b>a$.
Функція$f$ є спадною функцією на відкритому інтервалі якщо$f(b)<f(a)$ для кожного$a$,$b$ інтервал де$b>a$.

Функція$f$ має локальний максимум$b$ у точці відкритого інтервалу,$(a,c)$ якщо$f(b)$ вона більша або дорівнює$f(x)$ для кожної точки$x$ ($x$не дорівнює$b$) у інтервалі. Так само$f$ має локальний мінімум$b$ в точці,$(a,c)$ якщо$f(b)$ менше або дорівнює$f(x)$ для кожного$x$ ($x$не дорівнює$b$) в інтервалі.

Приклад$\PageIndex{7}$ Finding Increasing and Decreasing Intervals on a Graph

Враховуючи функцію на$p(t)$ малюнку$\PageIndex{6}$, визначте інтервали, на яких функція, як видається, збільшується.

[Графік многочлена.] — Малюнок$\PageIndex{6}$: Графік многочлена.

Рішення

Ми бачимо, що функція не є постійною на будь-якому інтервалі. Функція збільшується там, де вона нахиляється вгору, коли ми рухаємося вправо, і зменшується там, де вона нахиляється вниз, коли ми рухаємося вправо. Функція, здається, збільшується від$t=1$ до$t=3$ і$t=4$ від.

У інтервалі позначення, ми б сказали, що функція, здається, збільшується на інтервал$(1,3)$ і інтервал$(4,\infty)$.

Аналіз

Зверніть увагу в цьому прикладі, що ми використовували відкриті інтервали (інтервали, які не включають кінцеві точки), тому що функція не збільшується і не зменшується при$t=1$$t=3$, і$t=4$. Ці точки є локальними екстремумами (два мінімуми і максимум).

Приклад$\PageIndex{8}$: Finding Local Extrema from a Graph

Графік функції$f(x)=\frac{2}{x}+\frac{x}{3}$. Потім за допомогою графіка оцінюють локальні екстремуми функції і визначають інтервали, на яких функція збільшується.

Рішення

Використовуючи технологію, ми знаходимо, що графік функції виглядає так, як на рис$\PageIndex{7}$. Здається, є низька точка, або локальний мінімум, між$x=2$ і$x=3$, і дзеркальне зображення високої точки, або локальний максимум, десь між$x=−3$ і$x=−2$

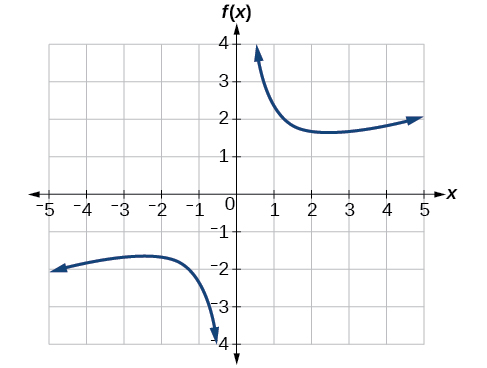Малюнок$\PageIndex{7}$: Графік зворотної функції.

Аналіз

Більшість графічних калькуляторів і графічних утиліт можуть оцінити розташування максимумів і мінімумів. Малюнок$\PageIndex{8}$ надає зображення екрану з двох різних технологій, що показують оцінку для локального максимуму і мінімуму.

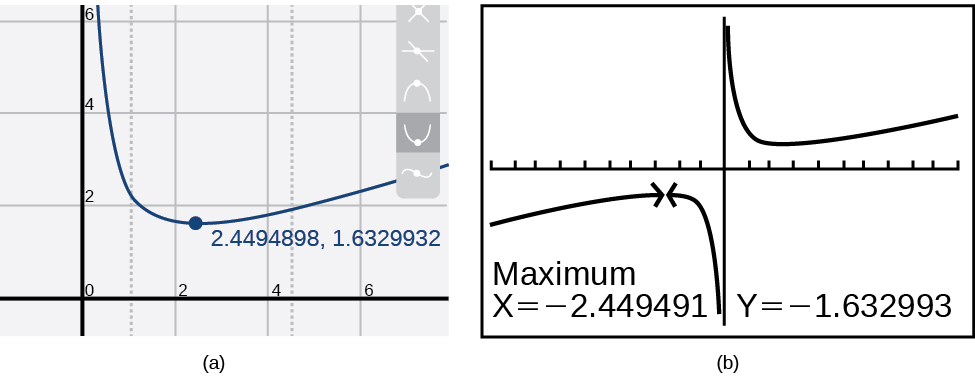
Рисунок$\PageIndex{8}$: Графік зворотної функції на графічному калькуляторі.

Виходячи з цих оцінок, функція збільшується на інтервалі$(−\infty,−2.449)$ і$(2.449,\infty)$. Зверніть увагу, що, хоча ми очікуємо, що крайність буде симетричною, дві різні технології узгоджуються лише до чотирьох десяткових знаків через різні алгоритми наближення, що використовуються кожним. (Точне розташування крайності знаходиться в$\pm\sqrt{6}$, але для визначення цього потрібно обчислення.)

Вправа$\PageIndex{8}$

$f(x)=x^3−6x^2−15x+20$Графік функції для оцінки локальних екстремумів функції. Використовуйте їх для визначення інтервалів, на яких функція збільшується і зменшується.

Рішення

Локальний максимум, як видається, відбувається при$(−1,28)$, а локальний мінімум відбувається при$(5,−80)$. Функція збільшується$(−\infty,−1)\cup(5,\infty)$ і зменшується на$(−1,5)$.

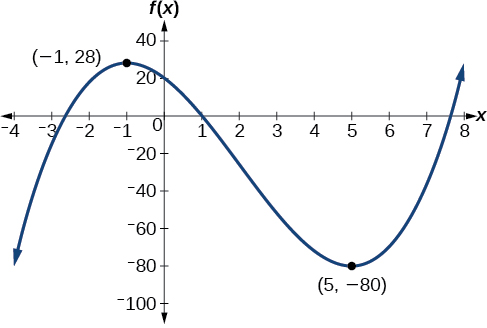
$Графік полінома з локальним максимумом при (-1, 28) і локальним мінімумом при (5, -80).$

Графік полінома з локальним максимумом при (-1, 28) і локальним мінімумом при (5, -80).

Приклад$\PageIndex{9}$: Finding Local Maxima and Minima from a Graph

Для функції f, графік якої показаний на малюнку$\PageIndex{9}$, знайдіть всі локальні максимуми і мінімуми.

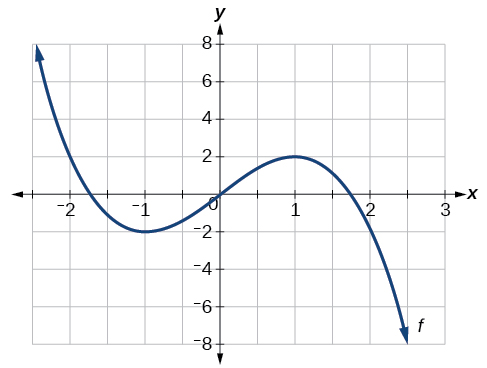
Рішення

Дотримуйтесь графіку$f$. Графік досягає локального максимуму,$x=1$ оскільки це найвища точка відкритого інтервалу навколо$x=1$ .Локальний максимум - це координата y$x=1$, яка дорівнює 2.

Графік досягає локального мінімуму,$x=−1$ оскільки це найнижча точка відкритого інтервалу навколо$x=−1$. Локальним мінімумом є y-координата$x=−1$, яка дорівнює −2.

Аналіз функцій інструментарію для збільшення або зменшення інтервалів

Тепер ми повернемося до функцій нашого інструментарію та обговоримо їх графічну поведінку на малюнку$\PageIndex{10}$$\PageIndex{11}$, рисунку та рисунку$\PageIndex{12}$.

$Таблиця із збільшенням та зменшенням інтервалів функцій інструментарію.$
Малюнок$\PageIndex{12}$

Використовуйте графік, щоб знайти абсолютний максимум і абсолютний мінімум

Існує різниця між розміщенням найвищої та найнижчої точок на графіку в регіоні навколо відкритого інтервалу (локально) та розташуванням найвищої та найнижчої точок на графіку для всього домену. Y-координати (вихід) у найвищій і найнижчій точках називаються абсолютним максимумом і абсолютним мінімумом відповідно. Щоб знайти абсолютні максимуми та мінімуми з графіка, нам потрібно спостерігати за графіком, щоб визначити, де графік досягає найвищої та найнижчої точок на області функції (рис.$\PageIndex{13}$).

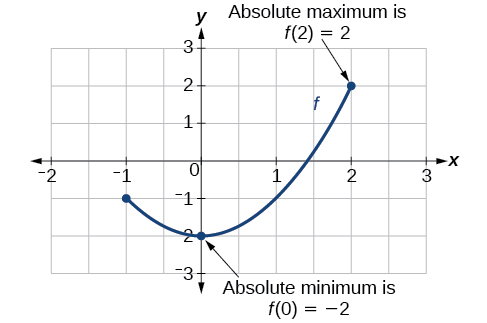
Графік відрізка параболи з абсолютним мінімумом at (0, -2) і абсолютним максимумом at (2, 2). — Рисунок$\PageIndex{13}$: Графік відрізка параболи з абсолютним мінімумом в (0, -2) і абсолютним максимумом при (2, 2).

Не кожна функція має абсолютне максимальне або мінімальне значення. Функція інструментарію$f(x)=x^3$ є однією з таких функцій.

Абсолютні максими і мінімуми

Абсолютний максимум$f$ at$x=c$ - це$f(c)$ де$f(c)≥f(x)$ для всіх$x$ у домені$f$.
Абсолютний мінімум$f$ at$x=d$ - це$f(d)$ де$f(d)≤f(x)$ для всіх$x$ в домені$f$.

Приклад$\PageIndex{10}$: Finding Absolute Maxima and Minima from a Graph

Для функції f, показаної на малюнку$\PageIndex{14}$, знайдіть всі абсолютні максимуми і мінімуми.

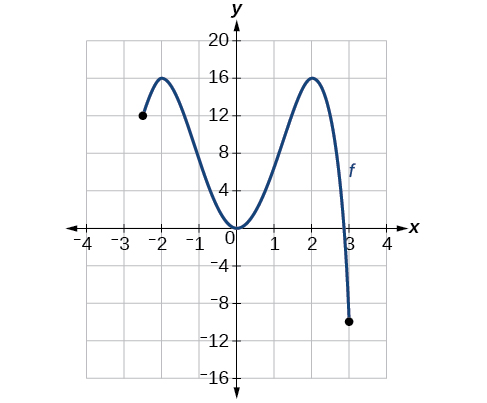
Рішення

Дотримуйтесь графіку$f$. Графік досягає абсолютного максимуму в двох місцях$x=2$,$x=−2$ і тому, що в цих місцях графік досягає найвищої точки в області функції. Абсолютним максимумом є$x=−2$ y-координата at$x=2$ and, яка дорівнює 16.

$Графік досягає абсолютного мінімуму при x=3, оскільки це найнижча точка в області графіка функції. Абсолютним мінімумом є y-координата при x=3, яка дорівнює -10.$

Ключові рівняння

Середня швидкість зміни:$\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}$

Ключові поняття

Швидкість зміни пов'язує зміну вихідної кількості зі зміною вхідної кількості. Середня швидкість зміни визначається з використанням тільки початкових і кінцевих даних. Див. Приклад.
Визначення точок, які позначають інтервал на графіку, можна використовувати для пошуку середньої швидкості зміни. Див. Приклад.
Порівняння пар вхідних і вихідних значень у таблиці також може бути використано для пошуку середньої швидкості зміни. Див. Приклад.
Середня швидкість зміни також може бути обчислена шляхом визначення значень функцій в кінцевих точках інтервалу, описаного формулою. Див. Приклад і Приклад.
Середня швидкість зміни іноді може бути визначена як вираз. Див. Приклад.
Функція збільшується там, де її швидкість зміни є позитивною, і зменшується, де її швидкість зміни негативна. Див. Приклад.
Локальний максимум - це місце, де функція змінюється від збільшення до зменшення і має вихідне значення більше (більше позитивного або менш негативного), ніж вихідні значення при сусідніх вхідних значеннях.
Локальний мінімум - це місце, де функція змінюється від зменшення до збільшення (у міру збільшення вхідних даних) і має вихідне значення менше (більше негативного або менш позитивного), ніж вихідні значення при сусідніх вхідних значеннях.
Мінімуми і максимуми також називають екстремами.
Ми можемо знайти локальні екстреми з графіка. Див. Приклад і Приклад.
Найвища і найнижча точки на графіку вказують максимуми і мінімуми. Див. Приклад.

\(y\)	2005	2006	2007	2008	2009	2010	2011	2012
\(C(y)\)	2.31	2.62	2.84	3.30	2.41	2.84	3.58	3.68

\(t\)(годин)	0	1	2	3	4	5	6	7
\(D(t)\)(милі)	10	55	90	153	214	240	292	300