4.1: Метод Ньютона

Last updated
Save as PDF

Page ID: 60675

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У главі 3 ми дізналися, як перша та друга похідні функції впливають на її графік. У цьому розділі ми досліджуємо інші застосування похідної.

Розв'язування рівнянь є однією з найважливіших речей, які ми робимо в математиці, але ми напрочуд обмежені в тому, що можемо вирішити аналітично. Наприклад, рівняння, такі прості, як$x^5+x+1=0$ або$\cos x =x$ не можуть бути розв'язані алгебраїчними методами з точки зору звичних функцій. На щастя, існують методи, які можуть дати нам приблизні рішення подібних рівнянь. Ці методи зазвичай можуть дати правильне наближення до стільки знаків після коми, скільки нам подобається. У розділі 1.5 ми дізналися про метод бісекції. Цей розділ присвячений іншій техніці (яка, як правило, працює швидше), яка називається Метод Ньютона.

Метод Ньютона будується навколо дотичних ліній. Основна ідея полягає в тому, що якщо$x$ досить близько до кореня$f(x)$, то дотична лінія до графіка за$(x,f(x))$ бажанням перетинає$x$ -вісь в точці ближче до кореня ніж$x$.

$альт$ $альт$ $альт$

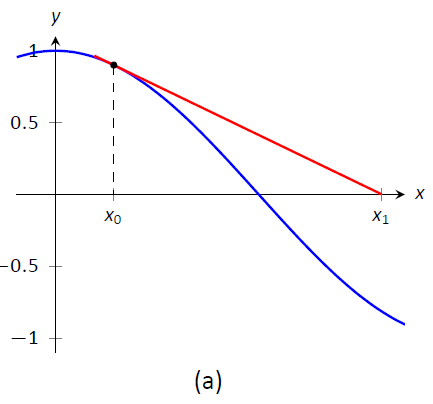
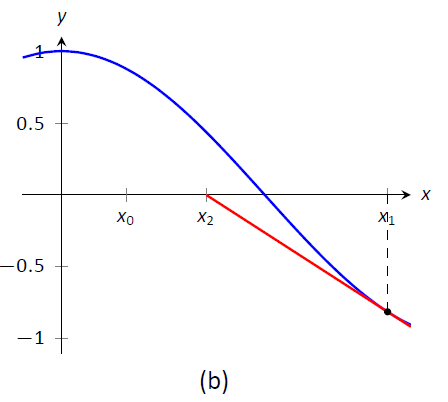
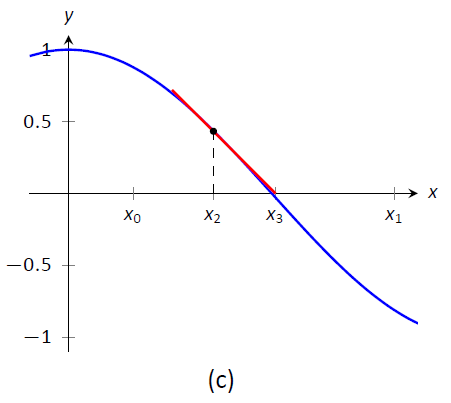
Малюнок$\PageIndex{1}$: Демонстрація геометричної концепції за методом Ньютона

Ми починаємо метод Ньютона з початкової здогадки про те, де знаходиться корінь. Назвіть це$x_0$. (Див$\PageIndex{1a}$. Рис.) Намалюйте дотичну лінію до графіка$(x_0,f(x_0))$ і подивіться, де вона відповідає$x$ осі -. Назвіть цей пункт$x_1$. Потім повторіть процес — намалюйте дотичну лінію до графіка$(x_1, f(x_1))$ та подивіться, де вона відповідає$x$ осі -. (Див$\PageIndex{1b}$. Рис.) Назвіть цей пункт$x_2$. Повторіть процес ще раз$x_3$, щоб отримати$x_4$, і т.д. ця послідовність точок часто сходиться досить швидко до кореня$f$.

Ми можемо використовувати цей геометричний процес для створення алгебраїчного процесу. Давайте розглянемо, як ми знайшли$x_1$. Ми почали з дотичної лінії до графіка в$(x_0,f(x_0))$. Нахил цієї дотичної лінії дорівнює$f'(x_0)$ і рівняння прямої дорівнює

$y=f' (x_0) (х-х_0) +ф (x_0).\]

Ця лінія перетинає$x$ вісь -коли$y=0$, а$x$ значення —значення, де вона перетинається, - це те, що ми називали$x_1$. Так давайте$y=0$ і$x$ замініть на$x_1$, даючи рівняння:

\[ 0 = f'(x_0)(x_1-x_0)+f(x_0).\]

Тепер вирішуйте для$x_1$:

\[x_1=x_0-\frac{f(x_0)}{f'(x_0)}.\]

Оскільки ми повторюємо той самий геометричний процес, щоб знайти$x_2$ з$x_1$, у нас є

\[x_2=x_1-\frac{f(x_1)}{f'(x_1)}.\]

Загалом, задавши наближення$x_n$, ми можемо знайти наступне наближення$x_{n+1}$, наступне:

\[x_{n+1} = x_{n} - \frac{f(x_{n})}{f'(x_{n})}.\]

Підсумовуємо цей процес наступним чином.

Ключова ідея 5: Метод Ньютона

$f$Дозволяти диференційовні функції на інтервалі$I$ з коренем в$I$. Щоб наблизити значення кореня, з точністю до$d$ десяткових знаків:

Виберіть значення$x_0$ як початкове наближення кореня. (Це часто робиться, дивлячись на графік$f$.)
Створюйте послідовні наближення ітераційно; задавши наближення$x_n$, обчислити наступне наближення$x_{n+1}$ як $$x_ {n+1} = x_n -\ frac {f (x_n)} {f' (x_n)} . $$
Зупиняйте ітерації, коли послідовні наближення не відрізняються в перших$d$ знаках після коми.

Примітка: Метод Ньютона не є непогрішним. Послідовність наближених значень може не сходитися, або вона може сходитися настільки повільно, що людина «обманюється» в мисленні певне наближення краще, ніж є насправді. Ці питання будуть розглянуті в кінці розділу.}

Давайте практикуємо метод Ньютона на конкретному прикладі.

Приклад$\PageIndex{1}$: Using Newton's Method

Наблизимо дійсний корінь$x^3-x^2-1=0$, з точністю до перших 3 знаків після десяткового числа, використовуючи метод Ньютона і початкове наближення$x_0=1$.}

Рішення

Для початку обчислюємо$f'(x)=3x^2-2x$. Потім застосовуємо алгоритм методу Ньютона, викладеного в Key Idea 5.

\[\begin{align} x_1&=1-\frac{f(1)}{f'(1)}=1-\frac{1^3-1^2-1}{3\cdot 1^2-2\cdot 1}=2,\\ x_2&=2-\frac{f(2)}{f'(2)}=2-\frac{2^3-2^2-1}{3\cdot 2^2-2\cdot 2}=1.625,\\ x_3&=1.625-\frac{f(1.625)}{f'(1.625)} = 1.625-\frac{1.625^3-1.625^2-1}{3\cdot 1.625^2-2\cdot 1.625}\approx 1.48579. \\ x_4 &= 1.48579 - \frac{f(1.48579)}{f'(1.48579)} \approx 1.46596\\ x_5 &= 1.46596 - \frac{f(1.46596)}{f'(1.46596)} \approx 1.46557 \end{align}\]

Ми виконали 5 ітерацій методу Ньютона, щоб знайти корінь з точністю до перших 3 знаків після коми; наше остаточне наближення -$1.465.$ точне значення кореня, до шести знаків після коми, є$1.465571$; Виявляється, що наш$x_5$ точний до більш ніж просто 3 знаків після коми.

Графік$f(x)$ наведено на рисунку$\PageIndex{2}$. З графіка ми бачимо, що наше початкове наближення не$x_0=1$ було особливо точним; ближче припущення було б$x_0=1.5$. Наш вибір базувався на простоті початкового розрахунку, і показує, що метод Ньютона може бути досить надійним, щоб нам не довелося робити дуже точне початкове наближення.

$альт$

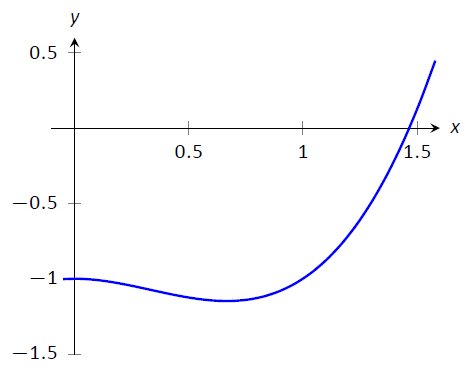
Малюнок$\PageIndex{2}$: Графік$f(x) = x^3-x^2-1$ у прикладі$\PageIndex{1}$.

Ми можемо автоматизувати цей процес на калькуляторі, який має ключ Ans, який повертає результат попереднього розрахунку. Почніть з натискання,$\texttt{1}$ а потім$\texttt{Enter}$. (Ми щойно ввели нашу початкову здогадку,$x_0=1$.) Тепер обчислюйте

$\ текст {Ans} -\ frac {f (\ textt {Ans})} {f' (\ текст {Ans})}\]

шляхом введення наступного і багаторазового натискання$\texttt{Enter}$ клавіші:

\[ \texttt{Ans}-(\texttt{Ans}^3-\texttt{Ans}^2-1)/(3*\texttt{Ans}^2-2*\texttt{Ans})\]

Щоразу, коли ми натискаємо клавішу\ texttt {Enter}, ми знаходимо послідовні наближення,,,$x_1$$x_2$,\ dots, і кожен з них наближається до кореня. Насправді, як тільки ми проходимо повз навколо$x_7$ або близько того, наближення, здається, не змінюються. Вони насправді змінюються, але зміна досить далеко праворуч від десяткової крапки, що вона не відображається на дисплеї калькулятора. Коли це станеться, ми можемо бути досить впевнені, що знайшли точне наближення.

Використання калькулятора таким чином робить обчислення простими; багато ітерацій можна обчислити дуже швидко.

Приклад$\PageIndex{2}$: Using Newton's Method to find where functions intersect

Використовуйте метод Ньютона, щоб наблизити рішення до$\cos{x} = x$, з точністю до 5 знаків після десяткової коми.

Рішення

Метод Ньютона надає метод розв'язування$f(x) = 0$; він не є (безпосередньо) методом розв'язання рівнянь подібного$f(x) = g(x)$. Однак це не проблема; ми можемо переписати останнє рівняння,$f(x) - g(x)=0$ а потім використовувати метод Ньютона.

Таким чином, ми переписуємо$\cos x=x$ як$\cos{x}-x=0$. Написано таким чином, ми знаходимо корінь$f(x)=\cos{x}-x$. Обчислюємо$f'(x)=-\sin{x} - 1$. Далі нам знадобиться стартове значення,$x_0$. Розглянемо Малюнок$\PageIndex{3}$, де$f(x) = \cos x-x$ зображено графіки. $x_0=0.75$Здається, що досить близько до кореня, тому ми будемо використовувати це як наш$x_0$. (На малюнку також показані графіки$y=\cos x$ і$y=x$, намальовані пунктирними лініями. Зверніть увагу, як вони перетинаються з тим же$x$ значенням, що і коли$f(x) = 0$.)

$альт$

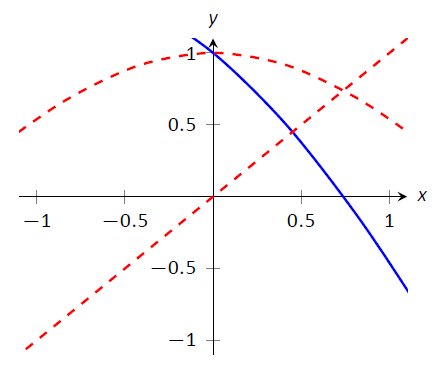
Малюнок$\PageIndex{3}$: Графік$f(x)=\cos x-x$ використовується для пошуку початкового наближення його кореня.

Ми тепер$x_1$ обчислюємо і$x_2$ т.д. формула$x_1$ для

\[x_1 = 0.75 - \frac{\cos(0.75)-0.75}{-\sin(0.75)-1}\approx 0.7391111388.\]

Застосуйте метод Ньютона ще раз, щоб знайти$x_2$:

\[x_2 = 0.7391111388 - \frac{\cos(0.7391111388)-0.7391111388}{-\sin(0.7391111388)-1}\approx 0.7390851334.\]

Ми можемо продовжувати цей шлях, але насправді найкраще автоматизувати цей процес. На калькуляторі з клавішею Ans ми б почали з натискання 0.75, потім$\texttt{Enter}$, введення нашого початкового наближення. Потім вводимо:

\[\texttt{Ans - (cos(Ans)-Ans)/(-sin(Ans)-1).}\]

Багаторазове натискання$\texttt{Enter}$ клавіші дає послідовні наближення. Швидко знаходимо:

\[ \begin{align} x_3 &= 0.7390851332\\ x_4 &= 0.7390851332. \end{align} \]

Наші наближення$x_2$ і$x_3$ не відрізнялися принаймні перші 5 знаків після десяткової, так що ми могли б зупинитися. Однак скористатися нашим калькулятором описаним способом нескладно, тому знайти не$x_4$ складе труднощів. Цікаво подивитися, як ми знайшли наближення, точне до такої кількості десяткових знаків, скільки відображає наш калькулятор, всього за 4 ітерації.

Якщо ви вмієте програмувати, ви можете перевести наступний псевдокод на улюблену мову, щоб виконати обчислення в цій задачі.

$\texttt{x = .75}$
$\texttt{while true}$
$\texttt{oldx = x}$
$\texttt{x = x - (cos(x)-x)/(-sin(x)-1)}$
$\texttt{print x}$
$\texttt{if abs(x-oldx) < .0000000001}$
$\texttt{break}$

Цей код обчислює і$x_1$$x_2$ т.д., зберігаючи кожен результат у змінній$\texttt{x}$. Попереднє наближення зберігається в змінній$\texttt{oldx}$. Ми продовжуємо цикл до тих пір, поки різниця між двома послідовними наближеннями$\texttt{abs(x-oldx)}$, не буде менше, ніж деякі малі допуски, в даному випадку,$\texttt{.0000000001}$.

Конвергенція методу Ньютона

Що слід використовувати для початкового припущення$x_0$? Як правило, чим ближче до фактичного кореня початкова здогадка, тим краще. Однак слід уникати деяких початкових здогадок. Наприклад, розглянемо приклад,$\PageIndex{1}$ де ми шукали корінь до$f(x) = x^3-x^2-1$. Вибір був$x_0=0$ би особливо поганим вибором. Розглянемо Малюнок$\PageIndex{4}$$f(x)$, де зображений разом з його дотичною лінією в$x=0$. Так як$f'(0)=0$, дотична лінія горизонтальна і не перетинається з$x$ віссю —. Графічно ми бачимо, що метод Ньютона виходить з ладу.

$альт$

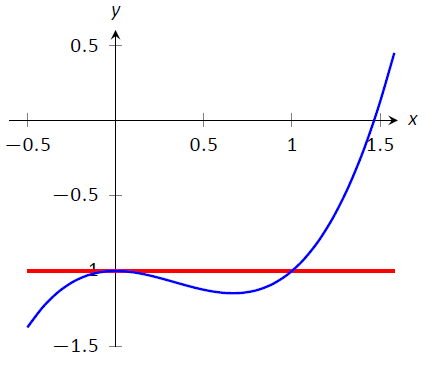
\ Рисунок$\PageIndex{4}$: Графік$f(x) = x^3-x^2-1$, який показує, чому початкове наближення$x_0=0$ методу Ньютона не вдається.

Ми також можемо аналітично бачити, що це не вдається. Так як

\[x_1 = 0 -\frac{f(0)}{f'(0)}\]

і$f'(0)=0$, ми бачимо, що$x_1$ це не дуже чітко визначено.

Ця проблема також може виникнути, якщо, наприклад, виявиться, що$f'(x_5)=0$. Регулювання початкового наближення$x_0$ на дуже невелику суму, швидше за все, усуне проблему.

Також можливо, що метод Ньютона не сходиться, тоді як кожне наступне наближення чітко визначено. Розглянемо$f(x) = x^{1/3}$, як показано на малюнку$\PageIndex{5}$. Зрозуміло, що корінь є$x=0$, але давайте наблизимо це с$x_0=0.1$. Малюнок$\PageIndex{5a}$ показує графічно розрахунок$x_1$; зверніть увагу, як він знаходиться далі від кореня ніж$x_0$. Цифри$\PageIndex{5b}$ і ($\PageIndex{5c}$) показують обчислення$x_2$ і$x_3$, які ще далі; наші послідовні наближення погіршуються. (Виявляється, в цьому конкретному прикладі кожне наступне наближення вдвічі більше від істинної відповіді, ніж попереднє наближення.)

$альт$ $альт$ $альт$

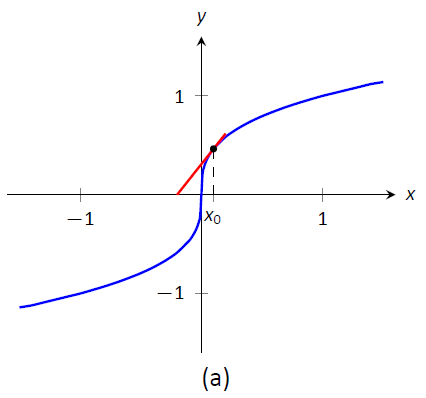
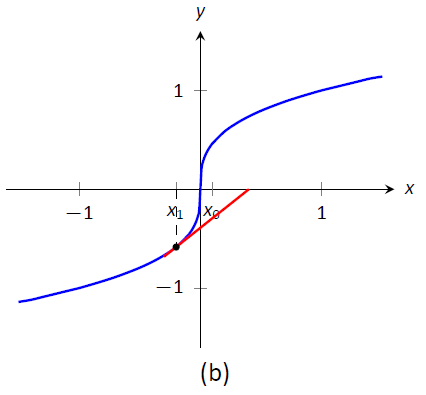
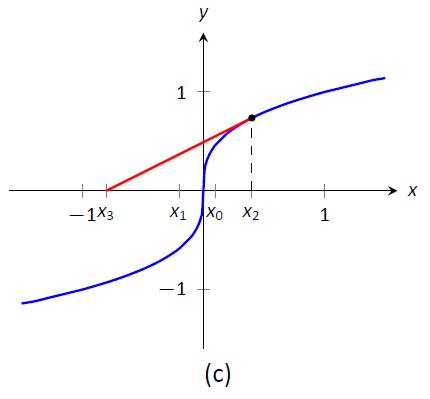
Рисунок$\PageIndex{5}$: Метод Ньютона не може знайти корінь$f(x) = x^{1/3}$, незалежно від вибору$x_0$.} \ label {fig:Ньют4}

Немає «виправлення» цієї проблеми; Метод Ньютона просто не спрацює, і потрібно використовувати інший метод.

Хоча метод Ньютона не завжди працює, він працює «більшу частину часу», і це, як правило, дуже швидко. Як тільки наближення наближаються до кореня, Метод Ньютона може вдвічі збільшити кількість правильних знаків після коми при кожному наступному наближенні. Курс з числового аналізу познайомить читача з більш ітераційними методами пошуку коренів, а також дасть більш детальну інформацію про сильні та слабкі сторони методу Ньютона.