4.1: Супутні тарифи

Last updated
Save as PDF

Page ID: 62171

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Експрес змінюються величини в терміні похідних.
Знайдіть зв'язки між похідними в даній задачі.
Використовуйте правило ланцюга, щоб знайти швидкість зміни однієї величини, яка залежить від швидкості зміни інших величин.

Ми бачили, що для величин, які змінюються з часом, темпи, з якими ці величини змінюються, задаються похідними. Якщо дві пов'язані величини змінюються з плином часу, ставки, з якими змінюються величини, пов'язані. Наприклад, якщо балон наповнюється повітрям, збільшується і радіус балона, і обсяг балона. У цьому розділі ми розглянемо кілька проблем, в яких змінюються дві або більше пов'язаних величин і вивчимо, як визначити залежність між темпами зміни цих величин.

Налаштування проблем, пов'язаних з тарифами

У багатьох реальних додатках пов'язані величини змінюються щодо часу. Наприклад, якщо знову розглянути приклад повітряної кулі, то можна сказати, що швидкість зміни обсягу$V$, пов'язана зі швидкістю зміни радіуса,$r$. У цьому випадку ми говоримо, що$\frac{dV}{dt}$ і$\frac{dr}{dt}$ пов'язані ставки, тому що$V$ це пов'язано з$r$. Тут ми вивчаємо кілька прикладів пов'язаних величин, які змінюються щодо часу, і ми розглянемо, як розрахувати одну швидкість зміни, враховуючи іншу швидкість зміни.

Приклад$\PageIndex{1}$: Inflating a Balloon

Сферичний балон наповнюється повітрям з постійною швидкістю$2\,\text{cm}^3\text{/sec}$ (рис.$\PageIndex{1}$). Як швидко збільшується радіус, коли радіус дорівнює$3$ см?

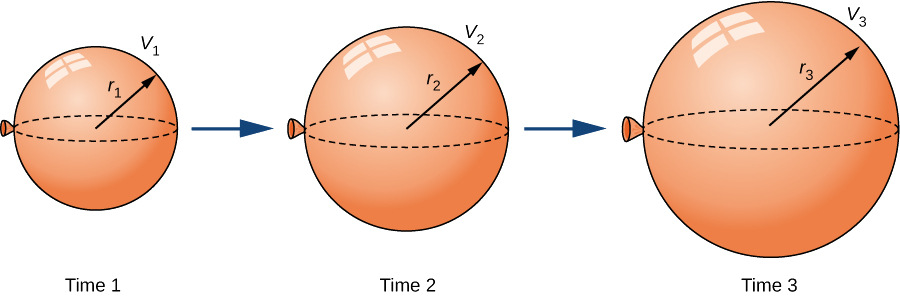
Три повітряні кулі показані в Часи 1, 2 і 3. Ці кульки збільшуються в об'ємі і радіусі зі збільшенням часу. — Малюнок$\PageIndex{1}$: Коли повітряна куля наповнюється повітрям, і радіус, і об'єм збільшуються по відношенню до часу.

Рішення

Обсяг сфери радіусом$r$ сантиметрів дорівнює

$V=\frac{4}{3}πr^3\,\text{cm}^3.$

Оскільки балон наповнюється повітрям, і обсяг, і радіус є функціями часу. Тому через$t$ секунди після початку заповнення повітряної кулі об'єм повітря в балоні становить

$V(t)=\frac{4}{3}π\big[r(t)\big]^3\text{cm}^3.$

Диференціюючи обидві сторони цього рівняння по відношенню до часу і застосовуючи правило ланцюга, ми бачимо, що швидкість зміни обсягу пов'язана зі швидкістю зміни радіуса рівнянням

$V'(t)=4π\big[r(t)\big]^2r′(t).$

Балон наповнюється повітрям з постійною швидкістю$2 \,\text{cm}^3\text{/sec}$, так$V'(t)=2\,\text{cm}^3\text{/sec}$. Тому,

$2\,\text{cm}^3\text{/sec}=\Big(4π\big[r(t)\big]^2\;\text{cm}^2\Big)⋅\Big(r'(t)\;\text{cm/s}\Big),$

що має на увазі

$r'(t)=\dfrac{1}{2π\big[r(t)\big]^2}\;\text{cm/sec}$.

Коли радіус$r=3$ см,

$r'(t)=\dfrac{1}{18π}\;\text{cm/sec}.$

Вправа$\PageIndex{1}$

Яка миттєва швидкість зміни радіуса при$r=6$ см?

Підказка: $\dfrac{dr}{dt}=\dfrac{1}{2πr^2}$

Відповідь: $\frac{1}{72π}$см/сек, або приблизно 0,0044 см/сек

Перш ніж розглядати інші приклади, давайте окреслимо стратегію вирішення проблем, яку ми будемо використовувати для вирішення проблем, пов'язаних зі ставками.

Стратегія вирішення проблем: вирішення проблеми пов'язаних ставок

Призначте символи всім змінним, що беруть участь у проблемі. Намалюйте фігуру, якщо це можливо.
Держава, з точки зору змінних, інформація, яка дається, і швидкість, яка повинна бути визначена.
Знайдіть рівняння, що стосується змінних, представлених на кроці 1.
Використовуючи правило ланцюга, диференціюйте обидві сторони рівняння, знайденого на кроці 3, щодо незалежної змінної. Це нове рівняння буде співвідносити похідні.
Підставити всі відомі значення в рівняння з кроку 4, потім вирішити для невідомої швидкості зміни

Зауважте, що при вирішенні проблеми пов'язаних ставок дуже важливо не підставляти відомі значення занадто рано. Наприклад, якщо значення змінної кількості підставляється в рівняння до того, як обидві сторони рівняння будуть диференційовані, то ця величина буде вести себе як постійна, і її похідна не з'явиться в новому рівнянні, знайденому на кроці 4. Ми розглядаємо цю потенційну помилку в наступному прикладі.

Приклади процесу

Давайте тепер реалізуємо щойно описану стратегію для вирішення декількох проблем, пов'язаних зі ставками. Перший приклад передбачає літак, що летить над головою. Взаємозв'язок, яку ми вивчаємо, полягає між швидкістю літака і швидкістю, з якою змінюється відстань між площиною і людиною на землі.

Приклад$\PageIndex{2}$: An Airplane Flying at a Constant Elevation

Літак летить над головою на постійній висоті$4000$ футів. Людина розглядає літак з позиції$3000$ футів від основи радіовежі. Літак летить горизонтально від людини. Якщо літак летить зі швидкістю$600$ ft/sec, з якою швидкістю відстань між людиною і літаком збільшується, коли літак проходить над радіовежею?

Рішення

Крок 1. Намалюйте малюнок, вводячи змінні для представлення різних величин, що беруть участь.

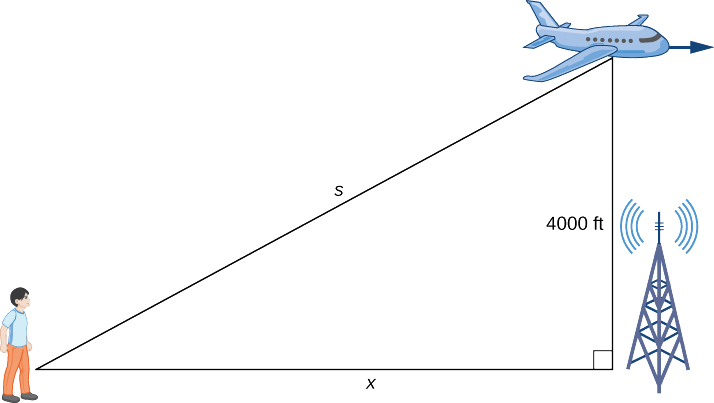
Прямокутний трикутник робиться з людиною на землі, літаком в повітрі і радіовежею під прямим кутом на землі. Гіпотенуза - s, відстань на землі між людиною і радіовежею дорівнює x, а сторона, протилежна людині (тобто висота від землі до літака) - 4000 футів. — Малюнок$\PageIndex{2}$: Літак летить на постійній висоті$4000$ футів. Відстань між людиною і літаком і людиною і місце на землі безпосередньо під літаком змінюються. Позначимо ці величини зі змінними$s$ і$x$, відповідно.

Як показано,$x$ позначає відстань між людиною і положення на землі безпосередньо під літаком. Змінна$s$ позначає відстань між людиною і площиною. Зверніть увагу, що обидва$x$ і$s$ є функціями часу. Ми не вводимо змінну для висоти площини, оскільки вона залишається на постійній висоті$4000$ футів. Оскільки висота об'єкта над землею вимірюється як найкоротша відстань між об'єктом та землею, відрізок лінії довжиною 4000 футів перпендикулярний відрізку лінії$x$ футів довжини, створюючи прямокутний трикутник.

Крок 2. Так як$x$ позначає горизонтальну відстань між людиною і точкою на землі під площиною,$dx/dt$ являє собою швидкість площини. Нам кажуть, що швидкість літака становить$600$ ft/sec. Тому$\frac{dx}{dt}=600$ фут/сек. Оскільки нас просять знайти швидкість зміни відстані між людиною та літаком, коли літак знаходиться безпосередньо над радіовежею, нам потрібно знайти,$ds/dt$ коли$x=3000$ фут.

Крок 3. З малюнка ми можемо використовувати теорему Піфагора, щоб написати рівняння, що стосується$x$ і$s$:

$[x(t)]^2+4000^2=[s(t)]^2.$

Крок 4. Диференціюючи це рівняння по відношенню до часу і використовуючи той факт, що похідна константи дорівнює нулю, приходимо до рівняння

\[x\frac{dx}{dt}=s\frac{ds}{dt}.\nonumber \]

Крок 5. Знайдіть швидкість, з якою відстань між людиною і літаком збільшується, коли літак знаходиться безпосередньо над радіовежею. Тобто знайти,$\frac{ds}{dt}$ коли$x=3000$ фут. Так як швидкість літака$600$ ft/sec, ми знаємо, що$\frac{dx}{dt}=600$ ft/sec. Нам не дається явне значення для$s$; однак, оскільки ми намагаємося знайти,$\frac{ds}{dt}$ коли$x=3000$ ft, ми можемо використовувати теорему Піфагора, щоб визначити відстань,$s$ коли$x=3000$ ft, а висота -$4000$ ft. Розв'язування рівняння

$3000^2+4000^2=s^2$

бо$s$, у нас є$s=5000$ фут на момент зацікавленості. Використовуючи ці значення, робимо висновок, що$ds/dt$

є розв'язком рівняння

$(3000)(600)=(5000)⋅\dfrac{ds}{dt}$.

Тому,

$\dfrac{ds}{dt}=\dfrac{3000⋅600}{5000}=360\,\text{ft/sec}.$

Примітка: При вирішенні проблем із спорідненими ставками важливо не підставляти значення змінних занадто рано. Наприклад, на кроці 3 ми пов'язували змінні величини$x(t)$ та$s(t)$ рівнянням

$[x(t)]^2+4000^2=[s(t)]^2.$

Оскільки площина залишається на постійній висоті, не потрібно вводити змінну для висоти, і нам дозволяється використовувати константу 4000 для позначення цієї величини. Однак інші дві величини змінюються. Якби ми помилково$x(t)=3000$ підставили рівняння перед диференціюванням, наше рівняння було б

$3000^2+4000^2=[s(t)]^2.$

Після диференціації наше рівняння стане

$0=s(t)\dfrac{ds}{dt}.$

В результаті ми б неправильно зробили висновок, що$\frac{ds}{dt}=0.$

Вправа$\PageIndex{2}$

Яка швидкість літака, якщо відстань між людиною і літаком збільшується зі швидкістю$300$ ft/sec?

Підказка: $\dfrac{ds}{dt}=300$фут/сек

Відповідь: $500$фут/сек

Тепер повернемося до проблеми, пов'язаної з запуском ракети з початку глави.

Приклад$\PageIndex{3}$: Chapter Opener - A Rocket Launch

Запускається ракета так, щоб вона піднімалася вертикально. Камера розташована на відстані$5000$ футів від стартового майданчика. Коли ракета знаходиться$1000$ над стартовим майданчиком, її швидкість становить$600$ ft/sec.

Фото ракети, що піднімається. — Малюнок$\PageIndex{3}$: (кредит: модифікація роботи Стіва Джурветсона, Wikimedia Commons)

Знайдіть необхідну швидкість зміни кута камери в залежності від часу, щоб вона залишалася зосередженою на ракеті.

Рішення

Крок 1. Намалюйте картинку, вводячи змінні.

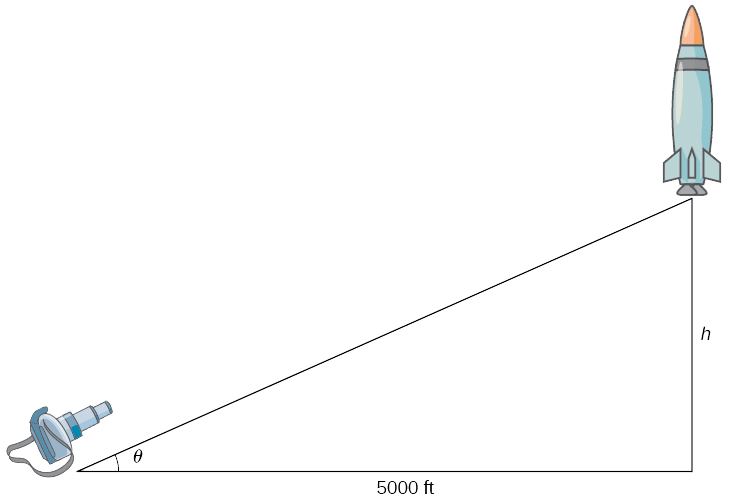
Прямокутний трикутник утворюється з камерою під одним з непрямих кутів і ракетою під іншим непрямим кутом. Кут з камерою має вимір θ. Відстань від ракети до землі - h; зверніть увагу, що це сторона, протилежна куту з мірою θ. Сторона, що прилягає до кута з мірою θ, становить 5000 футів. — Малюнок$\PageIndex{4}$: Камера розташована на$5000$ футах від стартового майданчика ракети. Висота ракети і кут нахилу камери змінюються щодо часу. Позначимо ці величини зі змінними$h$ і$θ$, відповідно.

Нехай$h$ позначають висоту ракети над стартовим майданчиком і$θ$ будуть кут між об'єктивом камери і землею.

Крок 2. Ми намагаємося знайти швидкість зміни кута нахилу камери щодо часу, коли ракета знаходиться на 1000 футів від землі. Тобто нам потрібно знайти,$\frac{dθ}{dt}$ коли$h=1000$ фут. У той час ми знаємо, що швидкість ракети становить$\frac{dh}{dt}=600$ ft/sec.

Крок 3. Тепер нам потрібно знайти рівняння, що стосується двох величин, які змінюються щодо часу:$h$ і$θ$. Як ми можемо створити таке рівняння? Використовуючи те, що ми намалювали прямокутний трикутник, природно думати про тригонометричних функціях. Нагадаємо, що$\tan θ$ це відношення довжини протилежної сторони трикутника до довжини сусідньої сторони. Таким чином, ми маємо

$\tan θ=\dfrac{h}{5000}$.

Це дає нам рівняння

$h=5000\tan θ.$

Крок 4. Диференціюючи це рівняння по відношенню до часу$t$, отримаємо

$\dfrac{dh}{dt}=5000\sec^2θ\dfrac{dθ}{dt}$.

Крок 5. Ми хочемо знайти,$\frac{dθ}{dt}$ коли$h=1000$ фут. На даний момент ми знаємо, що$\frac{dh}{dt}=600$ ft/sec. Потрібно визначитися$\sec^2θ$. Нагадаємо, що$\sec θ$ це відношення довжини гіпотенузи до довжини сусідньої сторони. Ми знаємо, що довжина сусідньої сторони$5000$ футів. Для визначення довжини гіпотенузи використовуємо теорему Піфагора, де довжина одного катета -$5000$ ft, довжина іншого катета -$h=1000$ ft, а довжина гіпотенузи -$c$ фути, як показано на наступному малюнку.

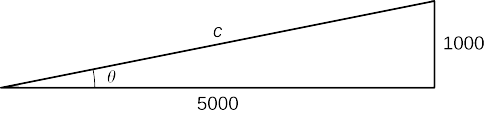
$Прямокутний трикутник має один кут з мірою θ. Гіпотенуза - c, довжина сторони, протилежна куту з мірою θ, дорівнює 1000, а сторона, прилегла до кута з мірою θ - 5000.$

Ми бачимо, що

$1000^2+5000^2=c^2$

і робимо висновок, що гіпотенуза

$c=1000\sqrt{26}\,\text{ft}.$

Тому, коли у$h=1000,$ нас є

$\sec^2θ=\left(\dfrac{1000\sqrt{26}}{5000}\right)^2=\dfrac{26}{25}.$

Нагадаємо з кроку 4, що рівняння, що$\frac{dθ}{dt}$ стосується наших відомих значень, є

$\dfrac{dh}{dt}=5000\sec^2θ\dfrac{dθ}{dt}.$

Коли$h=1000$ ft, ми знаємо, що$\frac{dh}{dt}=600$ ft/sec і$\sec^2θ=\frac{26}{25}$. Підставивши ці значення в попереднє рівняння, приходимо до рівняння

$600=5000\left(\frac{26}{25}\right)\dfrac{dθ}{dt}$.

Тому$\dfrac{dθ}{dt}=\dfrac{3}{26}$ рад/сек.

Вправа$\PageIndex{3}$

Яка швидкість зміни необхідна для кута підйому камери, якщо камера розміщена на землі на відстані$4000$ футів від стартового майданчика і швидкість ракети становить$500$ ft/sec, коли ракета знаходиться в$2000$ футах від землі?

Підказка: Знайти,$\frac{dθ}{dt}$ коли$h=2000$ фут. У той час,$\frac{dh}{dt}=500$ ft/sec.

Відповідь: $\frac{1}{10}$рад/сек

У наступному прикладі розглянемо злив води з конусоподібної воронки. Порівнюємо швидкість, з якою знижується рівень води в конусі з тією швидкістю, з якою зменшується обсяг води.

Приклад$\PageIndex{4}$: Water Draining from a Funnel

Вода стікає з дна конусоподібної воронки зі швидкістю$0.03\,\text{ft}^3\text{/sec}$. Висота воронки -$2$ фути, а радіус у верхній частині воронки -$1$ фути. З якою швидкістю змінюється висота води в воронці при висоті води$\frac{1}{2}$ футів?

Рішення

Крок 1: Намалюйте картинку, вводячи змінні.

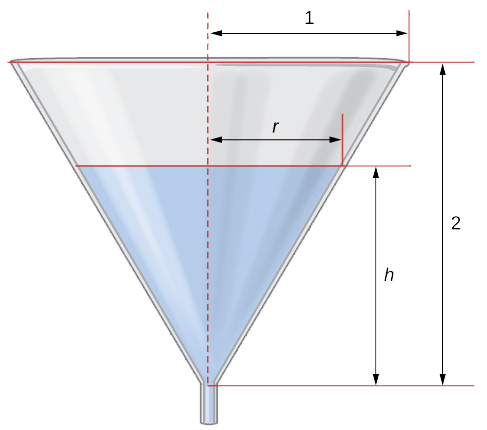
Відображається воронка з висотою 2 і радіусом 1 на її вершині. Воронка має воду на висоту h, в якій точці радіус дорівнює r. — Малюнок$\PageIndex{5}$: Вода стікає з воронки висотою$2$ футів і радіусом$1$ футів. Висота води і радіус води змінюються з плином часу. Позначимо ці величини зі змінними$h$ і$r$, відповідно.

Нехай$h$ позначають висоту води в воронці, r позначають радіус води у її поверхні, і$V$ позначають обсяг води.

Крок 2: Нам потрібно визначити,$\frac{dh}{dt}$ коли$h=\frac{1}{2}$ фут. Ми знаємо, що$\frac{dV}{dt}=−0.03$ ft/sec.

Крок 3: Обсяг води в конусі дорівнює

$V=\frac{1}{3}πr^2h.$

З малюнка ми бачимо, що у нас схожі трикутники. Тому співвідношення сторін у двох трикутників однакове. Тому$\frac{r}{h}=\frac{1}{2}$ або$r=\frac{h}{2}.$ Використовуючи цей факт, рівняння обсягу можна спростити до

$V=\frac{1}{3}π\left(\frac{h}{2}\right)^2h=\frac{π}{12}h^3$.

Крок 4: Застосовуючи правило ланцюга, диференціюючи обидві сторони цього рівняння щодо часу$t$, отримуємо

\[\frac{dV}{dt}=\frac{π}{4}h^2\frac{dh}{dt}.\nonumber \]

Крок 5: Ми хочемо знайти,$\frac{dh}{dt}$ коли$h=\frac{1}{2}$ фут. Так як вода йде зі швидкістю$0.03\,\text{ft}^3\text{/sec}$, ми це знаємо$\frac{dV}{dt}=−0.03\,\text{ft}^3\text{/sec}$. Тому,

\[−0.03=\frac{π}{4}\left(\frac{1}{2}\right)^2\dfrac{dh}{dt},\nonumber \]

що має на увазі

\[−0.03=\frac{π}{16}\dfrac{dh}{dt}.\nonumber \]

Звідси випливає, що

\[\dfrac{dh}{dt}=−\frac{0.48}{π}=−0.153\,\text{ft/sec}.\nonumber \]

Вправа$\PageIndex{4}$

З якою швидкістю змінюється висота води при висоті води$\frac{1}{4}$ футів?

Підказка: Нам потрібно знайти,$\frac{dh}{dt}$ коли$h=\frac{1}{4}.$

Відповідь: $−0.61$фут/сек

Ключові концепції

Щоб вирішити пов'язану проблему ставок, спочатку намалюйте картину, яка ілюструє взаємозв'язок між двома або більше пов'язаними величинами, які змінюються щодо часу.
Щодо величин, вкажіть надану інформацію та швидкість, яку потрібно знайти.
Знайдіть рівняння, що стосується величин.
Використовуйте диференціацію, застосовуючи правило ланцюга в міру необхідності, щоб знайти рівняння, яке пов'язує ставки.
Переконайтеся, що не підставляйте змінну величину для однієї зі змінних, поки не знайдіть рівняння, що стосується ставок.

Глосарій

пов'язані тарифи: це темпи зміни, пов'язані з двома або більше пов'язаними величинами, які змінюються з плином часу

Приклад\(\PageIndex{1}\): Inflating a Balloon

Вправа\(\PageIndex{1}\)

Стратегія вирішення проблем: вирішення проблеми пов'язаних ставок

Приклад\(\PageIndex{2}\): An Airplane Flying at a Constant Elevation

Вправа\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\): Chapter Opener - A Rocket Launch

Вправа\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\): Water Draining from a Funnel

Вправа\(\PageIndex{4}\)