2.6: Неявна диференціація

У попередніх розділах ми навчилися знаходити похідну$\frac{dy}{dx}$$y^\prime$, або, коли$y$ дається явно як функція$x$. Тобто, якщо ми знаємо$y=f(x)$ для якоїсь функції$f$, ми можемо знайти$y^\prime$. Наприклад, враховуючи$y=3x^2-7$, ми можемо легко знайти$y^\prime =6x$. (Тут ми чітко вказуємо, як$x$ і$y$ пов'язані. Знаючи$x$, ми можемо безпосередньо знайти$y$.)

Іноді зв'язок між$y$ і не$x$ є явним; скоріше, це неявне. Наприклад, ми можемо це знати$x^2-y=4$. Ця рівність визначає зв'язок між$x$ і$y$; якщо ми знаємо$x$, ми могли б з'ясувати$y$. Чи можемо ми все ще знайти$y^\prime$? У цьому випадку, звичайно; ми вирішуємо для$y$ отримання$y=x^2-4$ (отже, ми тепер знаємо$y$ явно), а потім диференціюємо, щоб отримати$y^\prime =2x$.

Іноді неявні відносини між$x$ і$y$ ускладнюються. Припустимо, нам дано$\sin(y)+y^3=6-x^3$. Графік цієї неявної функції наведено на малюнку 2.19. У цьому випадку немає абсолютно ніякого способу вирішити for$y$ в плані елементарних функцій. Дивно, однак, те, що ми все ще можемо знайти$y^\prime$ за допомогою процесу, відомого як неявна диференціація.

Малюнок 2.19: Графік неявної функції$\sin (y)+y^3=6-x^2$.

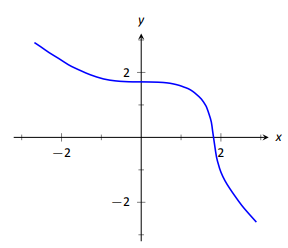
Неявна диференціація - це метод, заснований на Правилі ланцюга, який використовується для пошуку похідної, коли зв'язок між змінними задається неявно, а не явно (вирішується для однієї змінної з точки зору іншої).

Почнемо з перегляду правила ланцюга. $f$$g$Дозволяти і бути функціями$x$. Тоді $$\frac{d}{dx}\Big(f(g(x))\Big) = f^\prime(g(x))\cdot g'(x).$$ припустимо тепер, що$y=g(x)$. Ми можемо переписати вище, оскільки $$\frac{d}{dx}\Big(f(y))\Big) = f^\prime(y))\cdot y^\prime , \quad \text{or}\quad \frac{d}{dx}\Big(f(y))\Big)= f^\prime(y)\cdot \frac{dy}{dx}.\label{2.1}\tag{2.1}$$ ці рівняння виглядають дивно; ключова концепція для вивчення тут полягає в тому, що ми можемо знайти,$y^\prime$ навіть якщо ми точно не знаємо, як$y$ і$x$ пов'язані.

Ми демонструємо цей процес на наступному прикладі.

Приклад 67: Використання неявної диференціації

Знайти,$y^\prime$ враховуючи, що$\sin(y) + y^3=6-x^3$.

Рішення

Починаємо з взяття похідної обох сторін (таким чином зберігаючи рівність.) У нас є:

$$\frac{d}{dx}\Big(\sin(y) + y^3\Big)=\frac{d}{dx}\Big(6-x^3\Big).$$

Права сторона легка, вона повертається$-3x^2$.

Ліва сторона вимагає більшого розгляду. Беремо похідний термін — за терміном. Використовуючи техніку, отриману з рівняння 2.1 вище, ми бачимо, що $$\frac{d}{dx}\Big(\sin y\Big) = \cos y \cdot y^\prime .$$

Застосовуємо той же процес і до$y^3$ терміна.

$$\frac{d}{dx}\Big(y^3\Big) = \frac{d}{dx}\Big((y)^3\Big) = 3(y)^2\cdot y^\prime .$$

Поклавши це разом з правою стороною, ми маємо

$$\cos(y)y^\prime +3y^2y^\prime = -3x^2.$$

Тепер вирішуйте для$y^\prime$.

$$\begin{align*} \cos(y)y^\prime +3y^2y^\prime &= -3x^2.\\ \big(\cos y+3y^2\big)y^\prime &= -3x^2\\ y^\prime &= \frac{-3x^2}{\cos y+3y^2} \end{align*}$$

Це рівняння для$y^\prime$ напевно здається незвичним для нього містить як$x$ і$y$ терміни. Як його використовувати? Ми вирішимо це далі.

Неявні функції, як правило, важче мати справу, ніж з явними функціями. При явній функції, заданої$x$ значенням, ми маємо явну формулу обчислення відповідного$y$ значення. При неявній функції часто доводиться знаходити$x$ і$y$ значення одночасно, які задовольняють рівнянню. Набагато простіше продемонструвати, що задана точка задовольняє рівнянню, ніж насправді знайти таку точку.

Наприклад, ми можемо легко стверджувати, що точка$(\sqrt[3]{6},0)$ лежить на графіку неявної функції$\sin y + y^3=6-x^3$. $0$Підключивши для$y$, бачимо ліву сторону є$0$. Встановлюючи$x=\sqrt[3]6$, ми бачимо, що права сторона також$0$; рівняння задовольняється. Наступний приклад знаходить рівняння дотичної лінії до цієї функції в цій точці.

Приклад 68: Використання неявної диференціації для пошуку дотичної лінії

Знайти рівняння прямої дотичної до кривої неявно визначеної функції$\sin y + y^3=6-x^3$ в точці$(\sqrt[3]6,0)$.

Рішення

У прикладі 67 ми $$y^\prime = \frac{-3x^2}{\cos y +3y^2}.$$ виявили, що Ми знаходимо нахил дотичної лінії в точці$(\sqrt[3]6,0)$ шляхом підстановки$\sqrt[3]6$ for$x$ і$0$ for$y$. Таким чином, в точці$(\sqrt[3]6,0)$, ми маємо нахил як $$y^\prime = \frac{-3(\sqrt[3]{6})^2}{\cos 0 + 3\cdot0^2} = \frac{-3\sqrt[3]{36}}{1} \approx -9.91.$$

Тому рівняння дотичної лінії до неявно визначеної функції$\sin y + y^3=6-x^3$ в$(\sqrt[3]{6},0)$ точці крива і ця дотична лінія показані на малюнку 2.20. $$y = -3\sqrt[3]{36}(x-\sqrt[3]{6})+0 \approx -9.91x+18.$$

Малюнок 2.20: Функція$\sin y +y^3=6-x^2$ і її дотична лінія в точці$(\sqrt[3]{6},0)$.

Це говорить про загальний метод неявної диференціації. Для наведених нижче кроків припустимо$y$ це функція$x$.

1. Візьміть похідну кожного члена в рівнянні. Ставтеся до$x$ термінів як до нормальних. При прийомі похідних$y$ термінів застосовуються звичайні правила, за винятком того, що через Правило ланцюга нам потрібно помножити кожен член на$y^\prime$.
2. Отримайте всі$y^\prime$ терміни з одного боку знака рівності і поставте інші терміни з іншого боку.
3. Фактор поза$y^\prime$; вирішити для$y^\prime$ шляхом ділення.

Практичне зауваження: При роботі вручну може бути корисно використовувати символ$\frac{dy}{dx}$ замість$y^\prime$, оскільки останній можна легко сплутати для$y$ або$y^1$.

Приклад 69: Використання неявної диференціації

Дано неявно визначену функцію$y^3+x^2y^4=1+2x$, знайдіть$y^\prime$.

Рішення

Ми візьмемо неявні похідні термін за терміном. Похідне від$y^3$ є$3y^2y^\prime$.

Другий термін$x^2y^4$, трохи складний. Це вимагає Правило продукту, оскільки воно є добутком двох функцій$x$:$x^2$ і$y^4$. Його похідне є$x^2(4y^3y^\prime ) + 2xy^4$. Перша частина цього виразу вимагає а$y^\prime$ тому, що ми беремо похідну від$y$ терміна. Друга частина цього не вимагає, тому що ми беремо похідну від$x^2$.

Похідна правого боку легко знайти$2$. В цілому ми отримуємо:

$$3y^2y^\prime + 4x^2y^3y^\prime + 2xy^4 = 2.$$

Перемістіть терміни так, щоб ліва сторона складалася тільки з$y^\prime$ термінів, а права - з усіх інших термінів:

$$3y^2y^\prime + 4x^2y^3y^\prime = 2-2xy^4.$$

Фактор$y^\prime$ з лівого боку і вирішити, щоб отримати

$$y^\prime = \frac{2-2xy^4}{3y^2+4x^2y^3}.$$

Щоб підтвердити достовірність нашої роботи, знайдемо рівняння дотичної прямої до цієї функції в точці. Легко підтвердити, що точка$(0,1)$ лежить на графіку цієї функції. На даний момент,$y^\prime = 2/3$. Таким чином, рівняння дотичної лінії є$y = 2/3(x-0)+1$. Функція та її дотична лінія зображені на малюнку 2.21.

Малюнок 2.21: Графік неявно визначеної функції$y^3+x^2y^4 = 1+2x$ разом з її дотичною лінією в точці$(0,1)$.

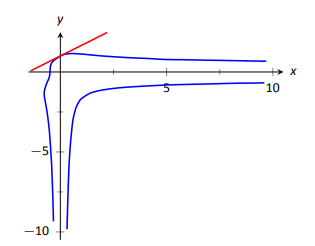
Зверніть увагу, як наша функція виглядає набагато інакше, ніж інші функції, які ми бачили. З одного боку, він не проходить тест вертикальної лінії. Такі функції важливі в багатьох областях математики, тому розробка інструментів для боротьби з ними також важлива.

Приклад 70: Використання неявної диференціації

Дано неявно визначену функцію$\sin(x^2y^2)+y^3=x+y$, знайдіть$y^\prime$.

Рішення

Диференціюючи термін за терміном, ми знаходимо найбільшу складність у першому семестрі. Це вимагає як ланцюга, так і правил продукту.

$$\begin{align*} \frac{d}{dx}\Big(\sin(x^2y^2)\Big) &= \cos(x^2y^2)\cdot\frac{d}{dx}\Big(x^2y^2\Big) \\ &= \cos(x^2y^2)\cdot\big(x^2(2yy^\prime )+2xy^2\big)\\ &= 2(x^2yy^\prime +xy^2)\cos(x^2y^2). \end{align*}$$

Похідні інших термінів залишаємо читачеві. Після взяття похідних обох сторін маємо

$$2(x^2yy^\prime +xy^2)\cos(x^2y^2) + 3y^2y^\prime = 1 + y^\prime .$$

Тепер ми повинні бути обережними$y^\prime$, щоб правильно вирішити, особливо через продукт зліва. Найкраще продукт примножити. Роблячи це, отримуємо

$$2x^2y\cos(x^2y^2)y^\prime + 2xy^2\cos(x^2y^2) + 3y^2y^\prime = 1 + y^\prime .$$

Звідси ми можемо безпечно рухатися по термінам, щоб отримати наступне:

$$2x^2y\cos(x^2y^2)y^\prime + 3y^2y^\prime - y^\prime = 1 - 2xy^2\cos(x^2y^2).$$

Тоді ми можемо вирішити,$y^\prime$ щоб отримати

$$y^\prime = \frac{1 - 2xy^2\cos(x^2y^2)}{2x^2y\cos(x^2y^2)+3y^2-1}.$$

Графік цієї неявної функції наведено на малюнку 2.22. Легко перевірити, що точки$(0,0)$,$(0,1)$ і$(0,-1)$ все лежать на графіку. Ми можемо знайти нахили дотичних ліній в кожній з цих точок, використовуючи нашу формулу для$y^\prime$.

Малюнок 2.22: Графік неявно визначеної функції$\sin (x^2y^2)+y^3=x+y$.

В$(0,0)$, нахил є$-1$.

В$(0,1)$, нахил є$1/2$.

В$(0,-1)$, нахил теж$1/2$.

Дотичні лінії додані до графіка функції на малюнку 2.23.

Малюнок 2.23: Графік неявно визначеної функції$\sin (x^2y^2)+y^3=x+y$ та певних дотичних ліній.

Досить багато «відомих» кривих мають рівняння, які даються неявно. Ми можемо використовувати неявну диференціацію, щоб знайти нахил у різних точках цих кривих. Ми досліджуємо дві такі криві в наступних прикладах.

Приклад 71: Пошук нахилів дотичних ліній до кола

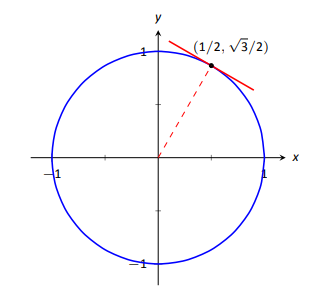
Знайдіть нахил дотичної лінії до кола$x^2+y^2=1$ в точці$(1/2, \sqrt{3}/2)$.

Рішення

Взявши похідні, отримуємо$2x+2yy^\prime =0$. Рішення для$y^\prime$ дарує: $$y^\prime = \frac{-x}{y}.$$

Це розумна формула. Нагадаємо, що нахил лінії через початок і точку$(x,y)$ на колі буде$y/x$. Ми виявили, що нахил дотичної лінії до кола в цій точці протилежний$y/x$, а саме,$-x/y$. Звідси ці дві лінії завжди перпендикулярні.

У точці$(1/2, \sqrt{3}/2)$ ми маємо нахил дотичної лінії як

$$y^\prime = \frac{-1/2}{\sqrt{3}/2} = \frac{-1}{\sqrt{3}} \approx -0.577.$$

Графік кола і її дотичної лінії при$(1/2,\sqrt{3}/2)$ наведено на малюнку 2.24 разом з тонкою пунктирною лінією від початку, яка перпендикулярна дотичній лінії. (Виходить, що всі нормальні лінії до кола проходять через центр кола.)

Малюнок 2.24: Одиничне коло з його дотичною лінією в$(1/2,\sqrt{3}/2)$.

У цьому розділі показано, як знайти похідні від неявно визначених функцій, графіки яких включають найрізноманітніші цікаві та незвичайні форми. Неявна диференціація також може бути використана для подальшого розуміння «регулярної» диференціації.

Одна дірка в нашому нинішньому розумінні похідних полягає в наступному: що таке похідна від функції квадратного кореня? Тобто, $$\frac{d}{dx}\big(\sqrt{x}\big) = \frac{d}{dx}\big(x^{1/2}\big) = \text{?}$$

Ми натякаємо на можливе рішення, оскільки ми можемо записати функцію квадратного кореня як степеневу функцію з раціональною (або, дробовою) потужністю. Потім ми спокушаємося застосувати Правило влади і отримати $$\frac{d}{dx}\big(x^{1/2}\big) = \frac12x^{-1/2} = \frac{1}{2\sqrt{x}}.$$

Проблема з цим полягає в тому, що Правило влади спочатку було визначено тільки для натуральних цілих степенів,$n>0$. Хоча ми не виправдовували це в той час, як правило влади доведено, використовуючи щось називається Біноміальна теорема, яка стосується тільки натуральних чисел. Правило частки дозволило нам розширити Правило влади на від'ємні цілі сили. Неявна диференціація дозволяє нам розширити Правило влади на раціональні повноваження, як показано нижче.

Нехай$y = x^{m/n}$, де$m$ і$n$ є цілими числами без загальних факторів (так$m=2$ і$n=5$ нормально, але$m=2$ і не$n=4$ є). Ми можемо переписати цю явну функцію неявно як$y^n = x^m$. Тепер застосовуємо неявну диференціацію.

\[\begin{align*}y &= x^{m/n} \\ y^n &= x^m \\ \frac{d}{dx}\big(y^n\big) &= \frac{d}{dx}\big(x^m\big) \\ n\cdot y^{n-1}\cdot y^\prime &= m\cdot x^{m-1} \\ y^\prime &= \frac{m}{n} \frac{x^{m-1}}{y^{n-1}} \quad \text{(now substitute $x^{m/n}$ for $y$)} \\ &= \frac{m}{n} \frac{x^{m-1}}{(x^{m/n})^{n-1}} \quad \text{(apply lots of algebra)}\\ &= \frac{m}n x^{(m-n)/n}\\ &= \frac{m}n x^{m/n -1}.\end{align*}\]

Вищевказана деривація є ключем до доказу, що поширює Правило влади на раціональні повноваження. Використовуючи обмеження, ми можемо ще раз розширити це, включивши всі сили, включаючи ірраціональні (навіть трансцендентні!) повноважень, даючи наступну теорему.

Теорема 21: Правило потужності для диференціації

Нехай$f(x) = x^n$, де$n\neq 0$ є дійсне число. Потім$f$ йде диференційована функція, і$f^\prime(x) = n\cdot x^{n-1}$.

Ця теорема дозволяє сказати похідну від$x^\pi$ є$\pi x^{\pi -1}$.

Тепер ми застосовуємо цю остаточну версію Правила влади в наступному прикладі, другому дослідженні «відомої» кривої.

Приклад 72: Використання правила живлення

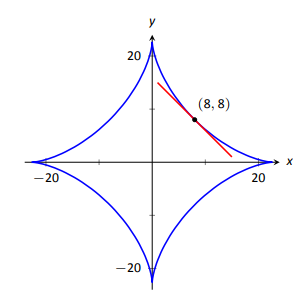
Знайдіть нахил$x^{2/3}+y^{2/3}=8$ в точці$(8,8)$.

Рішення

Це особливо цікава крива під назвою астроїд. Це форма, промальована точкою на краю кола, яка кочується всередині більшого кола, як показано на малюнку 2.25.

Малюнок 2.25: Астроїд, промальований точкою на меншому колі, коли він котиться всередині більшого кола.

Щоб знайти нахил астроїда в точці$(8,8)$, беремо похідну неявно.

$$\begin{align*} \frac23x^{-1/3}+\frac23y^{-1/3}y^\prime &=0\\ \frac23y^{-1/3}y^\prime &= -\frac23x^{-1/3}\\ y^\prime &= -\frac{x^{-1/3}}{y^{-1/3}}\\ y^\prime &= -\frac{y^{1/3}}{x^{1/3}} = -\sqrt[3]{\frac{y}x}. \end{align*}$$

Підключаємо$x=8$ і$y=8$, отримуємо ухил$-1$. Астроїд, з його дотичною лінією на$(8,8)$, показаний на малюнку 2.26.

Малюнок 2.26: Астроїд з дотичною лінією.

Неявна диференціація та друга похідна

Ми можемо використовувати неявну диференціацію, щоб знайти похідні вищого порядку. У теорії це просто: спочатку знайдіть$\frac{dy}{dx}$, потім візьміть його похідну щодо$x$. На практиці це не складно, але часто вимагає трохи алгебри. Ми демонструємо це на прикладі.

Приклад 73: Пошук другої похідної

Дано$x^2+y^2=1$, знайдіть$\frac{d^2y}{dx^2} = y^{\prime\prime}$.

Рішення

Ми виявили, що$y^\prime = \frac{dy}{dx} = -x/y$ в прикладі 71. Щоб знайти$y^{\prime\prime}$, застосовуємо неявну диференціацію до$y^\prime$.

$$\begin{align*} y^{\prime\prime} &= \frac{d}{dx}\big(y^\prime \big) \\ &= \frac{d}{dx}\left(-\frac xy\right)\qquad \text{(Now use the Quotient Rule.)} \\ &= -\frac{y(1) - x(y^\prime )}{y^2} \end{align*}$$

$y^\prime$замінити на$-x/y$:

$$\begin{align*}&= -\frac{y-x(-x/y)}{y^2} \\ &= -\frac{y+x^2/y}{y^2}.\end{align*}$$

Хоча це не особливо простий вираз, воно є корисним. Ми бачимо, що$y^{\prime\prime}>0$ коли$y<0$ і$y^{\prime\prime}<0$ коли$y>0$. У розділі 3.4 ми побачимо, як це стосується форми графіка.

Логарифмічна диференціація

Розглянемо функцію$y=x^x$; вона зображена на малюнку 2.27. Це добре визначено,$x>0$ і нам може бути цікаво знайти рівняння ліній, дотичних і нормальних до його графіку. Як ми беремо його похідне?

Малюнок 2.27: Сюжет о$y=x^x$.

Функція не є силовою функцією: вона має «силу»$x$, а не постійну. Це не експоненціальна функція: вона має «базу»$x$, а не константу.

Тут стає корисним метод диференціації, відомий як логарифмічна диференціація. Основний принцип полягає в наступному: візьміть природний журнал обох сторін рівняння$y=f(x)$, а потім використовуйте неявну диференціацію, щоб знайти$y^\prime$. Ми демонструємо це в наступному прикладі.

Приклад 74: Використання логарифмічної диференціації

Задано$y=x^x$, використовувати логарифмічну диференціацію для пошуку$y^\prime$.

Рішення

Як було запропоновано вище, ми починаємо з природного журналу обох сторін, а потім застосовуючи неявну диференціацію.

\[\begin{align*} y &= x^x \\ \ln (y) &= \ln (x^x) \text{(apply logarithm rule)}\\ \ln (y) &= x\ln x \text{(now use implicit differentiation)}\\ \frac{d}{dx}\Big(\ln (y)\Big) &= \frac{d}{dx}\Big(x\ln x\Big) \\ \frac{y^\prime }{y} &= \ln x + x\cdot\frac1x\\ \frac{y^\prime }{y} &= \ln x + 1\\ y^\prime &= y\big(\ln x+1\big) \text{(substitute $y=x^x$)}\\ y^\prime &= x^x\big(\ln x+1\big). \end{align*} \]

Щоб «перевірити» нашу відповідь, давайте використаємо його, щоб знайти рівняння дотичної прямої в$x=1.5$. Точка на графіку, через яку повинна пройти наша дотична лінія є$(1.5, 1.5^{1.5}) \approx (1.5, 1.837)$. Використовуючи рівняння для$y^\prime$, знаходимо нахил як

$$y^\prime = 1.5^{1.5}\big(\ln 1.5+1\big) \approx 1.837(1.405) \approx 2.582.$$

Таким чином рівняння дотичної прямої є$y = 1.6833(x-1.5)+1.837$. Малюнок 2.28 графіки$y=x^x$ разом з цією дотичною лінією.

Малюнок 2.22: Графік$y=x^x$ та його дотична лінія в$x=1.5$.

Неявна диференціація виявляється корисною, оскільки дозволяє знайти миттєві швидкості зміни різноманітних функцій. Зокрема, він розширив Правило влади на раціональні показники, які ми потім поширили на всі дійсні числа. У наступному розділі неявна диференціація буде використана для пошуку похідних обернених функцій, таких як$y=\sin^{-1} x$.