1.2: Визначення межі «Епсілон-Дельта»
- Page ID
- 60782
У цьому розділі представлено формальне визначення ліміту. Багато хто називає це «епсилон - дельта», визначення, посилаючись на\(\epsilon\) літери та\(\delta\) грецький алфавіт.
Перш ніж дати власне визначення, розглянемо кілька неформальних способів опису межі. З огляду на функцію\(y=f(x)\) і\(x\) -value\(c\), ми говоримо, що «межа функції\(f\), як\(x\) наближається\(c\), є значенням\(L\) «:
- якщо "\(y\)має тенденцію до\(L\)" як "\(x\)має тенденцію до»\(c\).
- якщо «\(y\)наближається\(L\)» як «\(x\)підходи»\(c\).
- якщо "\(y\)знаходиться поруч\(L\) «, коли"\(x\) знаходиться поруч»\(c\).
Проблема цих визначень полягає в тому, що слова «тяжіє», «наближення», а особливо «поруч» не є точними. Яким чином змінна,\(x\) як правило, або наближається,\(c\)? Наскільки поруч робити\(x\) і\(y\) повинні бути\(c\) і\(L\), відповідно?
Визначення, яке ми описуємо в цьому розділі, походить від формалізації 3. Швидке повторення наближає нас до того, що ми хочемо:
\(\textbf{3}^\prime\). Якщо\(x\) знаходиться в межах певного рівня допуску\(c\), то\(y=f(x)\) відповідне значення знаходиться в межах певного рівня допуску\(L\).
Традиційним позначенням для\(x\) -tolerance є мала грецька буква дельта\(\delta\), або, а\(y\) -tolerance позначається рядковим епсилон, або\(\epsilon\). Ще одне перефразування\(\textbf{3}^\prime\) майже доводить нас до фактичного визначення:
\(\textbf{3}^{\prime \prime}\). Якщо\(x\) знаходиться в межах\(\delta\) одиниць\(c\), то\(y\) відповідне значення знаходиться в межах\(\epsilon\) одиниць\(L\).
Ми можемо написати "\(x\)знаходиться в межах\(\delta\) одиниць\(c\)" математично як
\[|x-c| < \delta, \qquad \text{which is equivalent to }\qquad c-\delta < x < c+\delta.\]
Дозволяючи символу\(\longrightarrow\) "" представляти слово «означає», ми можемо переписати\(\textbf{3}''\) як
\[|x - c| < \delta \longrightarrow |y - L| < \epsilon \qquad \textrm{or} \qquad c - \delta < x < c + \delta \longrightarrow L - \epsilon < y < L + \epsilon.\]
Справа в тому, що\(\delta\) і\(\epsilon\), будучи допусками, можуть бути будь-якими позитивними (але, як правило, невеликими) значеннями. Нарешті, ми маємо формальне визначення межі з позначеннями, які бачили в попередньому розділі.
Визначення 1: Межа функції\(f\)
\(I\)Дозволяти бути відкритий інтервал\(c\), що містить, і нехай\(f\) бути функція визначена на\(I\), крім можливо в\(c\). Межа\(f(x)\), як\(x\) наближається\(c\)\(L\), є, позначається
\[ \lim_{x\rightarrow c} f(x) = L,\]
означає, що даний будь-який\(\epsilon > 0\), існує\(\delta > 0\) таке, що для всіх\(x\neq c\), якщо\(|x - c| < \delta\), то\(|f(x) - L| < \epsilon\).
(Математики часто люблять писати ідеї, не використовуючи жодних слів. Ось безсловесне визначення межі:
\[\lim_{x\rightarrow c} f(x) = L \iff \forall \, \epsilon > 0, \exists \, \delta > 0 \; s.t. \;0<|x - c| < \delta \longrightarrow |f(x) - L| < \epsilon .\text{)}\]
Зверніть увагу на порядок, в якому\(\epsilon\) і\(\delta\) даються. У визначенні спочатку\(\epsilon\) дається\(y\) -толерантність, а потім межа буде існувати, якщо ми зможемо знайти\(x\) -толерантність\(\delta\), яка працює.
Приклад допоможе нам розібратися в цьому визначенні. Зверніть увагу, що пояснення довге, але воно займе один через всі кроки, необхідні для розуміння ідей.
Приклад 6: Оцінка ліміту за допомогою визначення
Покажіть, що\(\lim\limits_{x\rightarrow 4} \sqrt{x} = 2 .\)
Рішення:
Перш ніж використовувати формальне визначення, давайте спробуємо деякі числові допуски. Що робити, якщо\(y\) допуск дорівнює 0,5, або\(\epsilon =0.5\)? Наскільки близько до 4\(x\) має бути так, що\(y\) знаходиться в межах 0,5 одиниць 2, тобто\(1.5 < y < 2.5\)? В цьому випадку можна поступити наступним чином:
\[\begin{align}1.5 &< y < 2.5 \\ 1.5 &< \sqrt{x} < 2.5\\ 1.5^2 &< x < 2.5^2\\ 2.25 &< x < 6.25.\\ \end{align}\]
Отже, яка бажана\(x\) толерантність? Пам'ятайте, ми хочемо знайти симетричний інтервал\(x\) значень, а саме\(4 - \delta < x < 4 + \delta\). Нижня\(2.25\) межа -\(1.75\) одиниці з 4; верхня межа 6,25 - 2,25 одиниць з 4. Нам потрібна менша з цих двох відстаней; ми повинні мати\(\delta \leq 1.75\). Див. Малюнок 1.17.
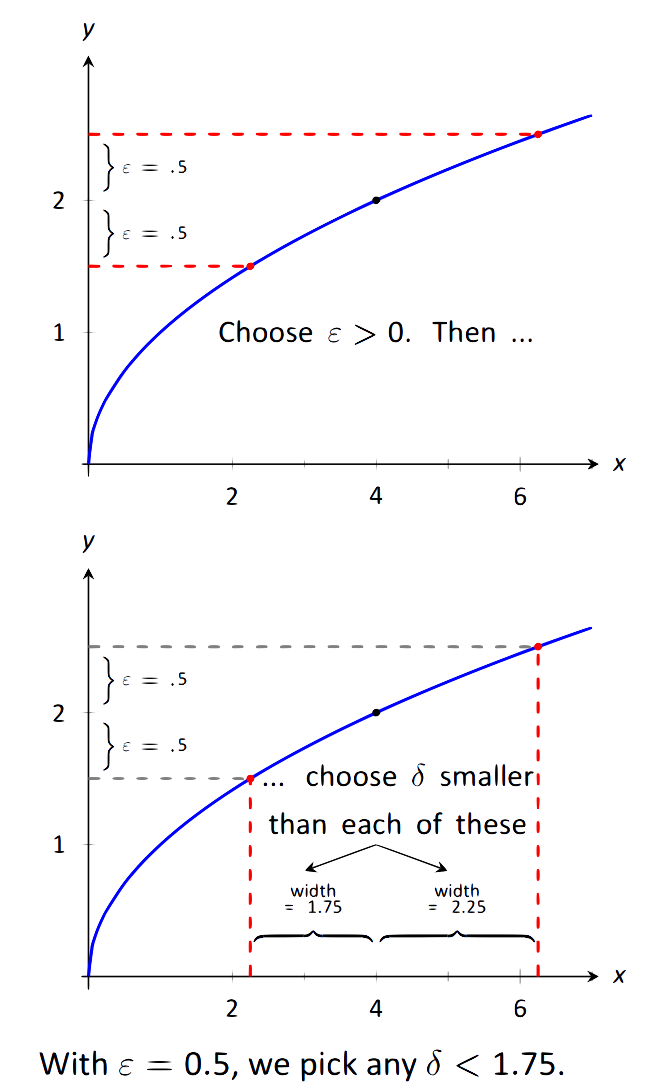
\(\text{FIGURE 1.17}\): Ілюстрація\(\epsilon - \delta\) процесу.
Враховуючи\(y\) толерантність\(\epsilon =0.5\), ми знайшли\(x\) толерантність\(\delta \leq 1.75\), таку, що всякий раз, коли\(x\) знаходиться в межах\(\delta\) одиниць 4, то\(y\) знаходиться в межах\(\epsilon\) одиниць 2. Це те, що ми намагалися знайти.
Спробуємо ще одне значення\(\epsilon\).
Що робити, якщо\(y\) допуск дорівнює 0,01, тобто\(\epsilon =0.01\)? Наскільки близько до 4\(x\) має бути для того,\(y\) щоб бути в межах 0,01 одиниць 2 (або\(1.99 < y < 2.01\))? Знову ж таки, ми просто квадрат ці значення, щоб отримати\(1.99^2 < x < 2.01^2\), або
\[3.9601 < x < 4.0401.\]
Яка бажана\(x\) толерантність? У цьому випадку ми повинні мати\(\delta \leq 0.0399\), що є мінімальною відстанню від 4 з двох меж, наведених вище.
Зверніть увагу, що в деякому сенсі, схоже, є два допуски (нижче 4 з 0.0399 одиниць і вище 4 з 0.0401 одиниць). Однак ми не могли використовувати більше значення\(0.0401\) for\(\delta\) з тих пір інтервал для\(x\)\(3.9599 < x < 4.0401\) призведе до\(y\) значення\(1.98995 < y < 2.01\) (який містить значення НЕ в межах 0,01 одиниць 2).
Що ми маємо поки що: якщо\(\epsilon =0.5\), то\(\delta \leq 1.75\) і якщо\(\epsilon = 0.01\), то\(\delta \leq 0.0399\). Візерунок побачити непросто, тому переходимо до загального\(\epsilon\) намагаємося визначити\(\delta\) символічно. Ми починаємо з припущення\(y=\sqrt{x}\), що знаходиться в межах\(\epsilon\) одиниць 2:
\[\begin{eqnarray*}|y - 2| < \epsilon &\\ -\epsilon < y - 2 < \epsilon& \qquad \textrm{(Definition of absolute value)}\\ -\epsilon < \sqrt{x} - 2 < \epsilon &\qquad (y=\sqrt{x})\\ 2 - \epsilon < \sqrt{x} < 2+ \epsilon &\qquad \textrm{ (Add 2)}\\ (2 - \epsilon)^2 < x < (2+ \epsilon) ^2 &\qquad \textrm{ (Square all)}\\ 4 - 4\epsilon + \epsilon^2 < x < 4 + 4\epsilon + \epsilon^2 &\qquad \textrm{ (Expand)}\\ 4 - (4\epsilon - \epsilon^2) < x < 4 + (4\epsilon + \epsilon^2). &\qquad \textrm{ (Rewrite in the desired form)}\end{eqnarray*}\]
«Бажана форма» на останньому кроці - "»\(4-\textit{something} < x < 4 +\textit{something}\). Оскільки ми хочемо, щоб цей останній інтервал описати\(x\) допуск навколо 4, ми маємо, що\(\delta \leq 4\epsilon - \epsilon^2\) або\(\delta \leq 4\epsilon + \epsilon^2\), залежно від того, що менше:
\[\delta \leq \min\{4\epsilon - \epsilon^2, 4\epsilon + \epsilon^2\}.\]
Так як\(\epsilon > 0\), мінімум є\(\delta \leq 4\epsilon - \epsilon^2\). Ось і формула: дано\(\epsilon\), множина\(\delta \leq 4\epsilon-\epsilon^2\).
Ми можемо перевірити це для наших попередніх значень. Якщо\(\epsilon=0.5\), формула дає\(\delta \leq 4(0.5) - (0.5)^2 = 1.75\) і коли\(\epsilon=0.01\), формула дає\(\delta \leq 4(0.01) - (0.01)^2 = 0.399\).
Так враховується будь-який\(\epsilon >0\), безліч\(\delta \leq 4\epsilon - \epsilon^2\). Тоді якщо\(|x-4|<\delta\) (і\(x\neq 4\)), то\(|f(x) - 2| < \epsilon\), задовольняючи визначенню межі. Ми показали формально (і нарешті!) що\( \lim_{x\rightarrow 4} \sqrt{x} = 2 \).
Насправді, це біль, але це не спрацює, якщо\(\epsilon \ge 4\). Це насправді не повинно відбуватися,\(\epsilon\) оскільки має бути невеликим, але це може статися. У тих випадках\(\epsilon \ge 4\), коли, просто візьміть\(\delta = 1\) і у вас все буде добре.
Попередній приклад був трохи довгим у тому, що ми вибрали кілька конкретних випадків\(\epsilon\) перед обробкою загальної справи. Зазвичай цього не роблять. Попередній приклад також трохи незадоволений у цьому\(\sqrt{4}=2\); навіщо так наполегливо працювати, щоб довести щось настільки очевидне? Багато\(\epsilon\) -\(\delta\) докази довго і важко зробити. У цьому розділі ми зупинимося на прикладах, де відповідь, чесно кажучи, очевидна, тому що неочевидні приклади ще важче. У наступному розділі ми дізнаємося деякі теореми, які дозволяють оцінювати межі аналітично, тобто без використання\(\epsilon\) -\(\delta\) визначення.
Ось чому теореми про межі так корисні! Зробивши ще кілька\(\epsilon\) -\(\delta\) доказів, ви дійсно оціните аналітичні «короткі скорочення», знайдені в наступному розділі.
Приклад 7: Оцінка ліміту за допомогою визначення
Покажіть, що\( \lim_{x\rightarrow 2} x^2 = 4\).
Рішення
Давайте зробимо цей приклад символічно з самого початку. Нехай\(\epsilon > 0\) дадуть; ми хочемо\(|y-4| < \epsilon\), т\(|x^2-4| < \epsilon\). Е. Як ми знаходимо\(\delta\) таке, що коли\(|x-2| < \delta\), нам це гарантовано\(|x^2-4|<\epsilon\)?
Це трохи складніше, ніж попередній приклад, але давайте почнемо з того, що помічаємо це\(|x^2-4| = |x-2|\cdot|x+2|\). Розглянемо:
\[ |x^2-4| < \epsilon \longrightarrow |x-2|\cdot|x+2| < \epsilon \longrightarrow |x-2| < \frac{\epsilon}{|x+2|}.\label{eq:limit1}\tag{1.1}\]
Чи не могли ми встановити\( \delta = \frac{\epsilon}{|x+2|}\)?
Ми близькі до відповіді, але підступ полягає в тому, що\(\delta\) повинно бути постійним значенням (тому воно не може містити\(x\)). Є спосіб обійти це, але ми повинні зробити припущення. Пам'ятайте, що\(\epsilon\) передбачається невелике число, що має на увазі, що також\(\delta\) буде невелике значення. Зокрема, ми можемо (ймовірно) припустити, що\(\delta < 1\). Якщо це правда, то\(|x-2| < \delta\) означало б\(|x-2| < 1\), що, даючи\(1 < x < 3\).
Тепер повернемося до фракції\( \frac{\epsilon}{|x+2|}\). Якщо\(1<x<3\), то\(3<x+2<5\) (додати 2 до всіх членів в нерівності). Беручи взаємні, ми маємо
\[\begin{align}\frac{1}{5} <& \frac{1}{|x+2|} < \frac {1}{3} & \text{which implies}\\ \frac{1}{5} <& \frac{1}{|x+2|} & \text{which implies}\\ \frac{\epsilon}{5}<&\frac{\epsilon}{|x+2|}.\label{eq:limit2}\tag{1.2}\end{align}\]
Це говорить про те, що ми встановили\( \delta \leq \frac{\epsilon}{5}\). Щоб зрозуміти, чому, давайте розглянемо, що слід, коли ми припускаємо\(|x-2|<\delta\):
\[\begin{align*}|x - 2| &< \delta &\\ |x - 2| &< \frac{\epsilon}{5}& \text{(Our choice of \(\delta\))}\\ |x - 2|\cdot|x + 2| &< |x + 2|\cdot\frac{\epsilon}{5}& \text{(Multiply by \(|x+2|\))}\\ |x^2 - 4|&< |x + 2|\cdot\frac{\epsilon}{5}& \text{(Combine left side)}\\ |x^2 - 4|&< |x + 2|\cdot\frac{\epsilon}{5}< |x + 2|\cdot\frac{\epsilon}{|x+2|}=\epsilon & \text{(Using (\ref{eq:limit2}) as long as \(\delta <1\))} \end{align*}\]
Ми приїхали за\(|x^2 - 4|<\epsilon\) бажанням. Зауважте ще раз, для того, щоб це сталося, нам потрібно\(\delta\) спочатку бути менше 1. Це безпечне припущення; ми\(\epsilon\) хочемо бути довільно малими,\(\delta\) змушуючи також бути малими.
Ми також\(\delta\) вирішили бути меншим, ніж «необхідно». Ми могли б обійтися трохи більшим\(\delta\), як показано на малюнку 1.18. Пунктирні зовнішні лінії показують межі, визначені нашим вибором\(\epsilon\). Пунктирні внутрішні лінії показують межі, визначені налаштуванням\(\delta = \epsilon/5\). Зверніть увагу, як ці пунктирні лінії знаходяться в пунктирних лініях. Це абсолютно добре; вибираючи\(x\) в межах пунктирних ліній, ми гарантуємо, що\(f(x)\) буде в межах\(\epsilon\) 4. % Якщо значення, яке ми врешті-решт використали\(\delta\)\(\epsilon/5\), а саме, не менше 1, це підтвердження не працюватиме. Для остаточного виправлення ми замість цього встановлюємо\(\delta\) мінімум 1 і\(\epsilon/5\). Таким чином працюють всі розрахунки вище.
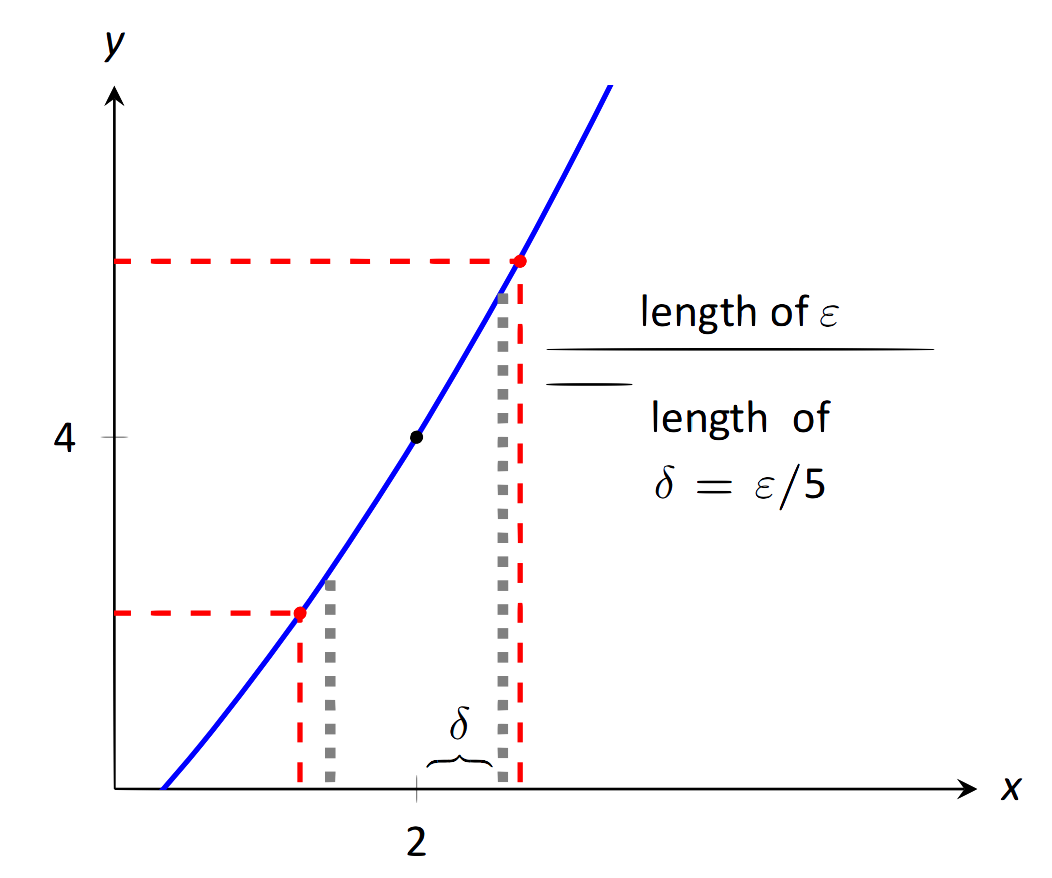
\(\text{FIGURE 1.18}\): Вибір\(\delta = \epsilon / 5 \) у прикладі 7.
Підсумовуючи, дано\(\epsilon > 0\), безліч\(\delta=\leq\epsilon/5\). Потім\(|x - 2| < \delta\) має на увазі\(|x^2 - 4|< \epsilon\) (тобто\(|y - 4|< \epsilon\)) за бажанням. Це показує, що\( \lim_{x\rightarrow 2} x^2 = 4 \). Рисунок 1.18 дає візуалізацію цього;\(x\) обмежуючись значеннями в межах\(\delta = \epsilon/5\) 2, ми бачимо, що\(f(x)\) знаходиться в межах\(\epsilon\)\(4\).
Зверніть увагу на загальний візерунок, виставлений в цих останніх двох прикладах. У якомусь сенсі кожен починається «назад». Тобто поки ми хочемо
- почати з\(|x-c|<\delta\) і зробити висновок, що
- \(|f(x)-L|<\epsilon\),
ми фактично починаємо з припускаючи
- \(|f(x)-L|<\epsilon\), Потім виконайте деякі алгебраїчні маніпуляції, щоб надати нерівність форми
- \(|x-c|<\)щось.
Коли ми правильно це зробили, щось на стороні нерівності «більше, ніж» стає нашим\(\delta\). Ми можемо називати це етапом «подряпина-робота» нашого доказу. Після того\(\delta\), як ми це зробимо, ми можемо формально почати з\(|x-c|<\delta\) і використовувати алгебраїчні маніпуляції\(|f(x)-L|<\epsilon\), щоб зробити висновок, що, як правило, використовуючи ті самі кроки нашої «подряпини-робота» у зворотному порядку.
Ми виділимо цей процес в наступному прикладі.
Приклад 8: Оцінка ліміту за допомогою визначення
Доведіть це\( \lim\limits_{x\rightarrow 1}x^3-2x = -1\).
Рішення
Ми починаємо нашу роботу з подряпин, враховуючи\(|f(x) - (-1)| < \epsilon\):
\[\begin{align} |f(x)-(-1)| &< \epsilon \\ |x^3-2x + 1|&< \epsilon & \text{(Now factor)}\\ |(x-1)(x^2+x-1)|&< \epsilon \\ |x-1| &<\frac{\epsilon}{|x^2+x-1|}.\label{eq:lim4}\tag{1.3} \end{align}\]
Ми знаходимося на етапі сказати, що\(|x-1|<\) щось, де\(\textit{something}=\epsilon/|x^2+x-1|\). Ми хочемо перетворити це на щось\(\delta\).
Оскільки\(x\) наближається до 1, ми можемо з упевненістю припустити, що\(x\) це між 0 і 2. Так
\[\begin{align*} 0&< x<2 & \\ 0&< x^2<4.&\text{(squared each term)}\\ \end{align*}\]
Так як\(0<x<2\), ми можемо додати\(0\)\(2\),\(x\) і, відповідно, до кожної частини нерівності і зберегти нерівність.
\[\begin{align*}0&< x^2+x<6 &\\ -1&< x^2+x-1<5.&\text{(subtracted 1 from each part)} \end{align*}\]
У рівнянні\ eqref {eq:lim4}, ми хотіли\(|x-1|<\epsilon/|x^2+x-1|\). Вищесказане показує, що з урахуванням будь-якого\(x\) в\([0,2]\), ми знаємо, що
\[\begin{align} x^2+x-1 &< 5 &\text{which implies that}\notag\\ \frac15 &< \frac{1}{x^2+x-1} &\text{which implies that}\notag\\ \frac{\epsilon}5 &< \frac{\epsilon}{x^2+x-1}.\label{eq:lim4b}\tag{1.4} \end{align}\]
Так ми і встановили\(\delta \leq \epsilon/5\). На цьому наша робота над подряпинами закінчується, і ми починаємо формальне підтвердження (що також допомагає нам зрозуміти, чому це був хороший вибір\(\delta\)).
Дано\(\epsilon\), нехай\(\delta \leq \epsilon/5\). Ми хочемо показати, що коли\(|x-1|<\delta\), тоді\(|(x^3-2x)-(-1)|<\epsilon\). Починаємо з\(|x-1|<\delta\):
\[\begin{align*} |x-1| &< \delta \\ |x-1| &< \frac{\epsilon}5\\ |x-1| &< \frac\epsilon5 < \frac{\epsilon}{|x^2+x-1|} & \text{(for \(x\) near 1, from Equation \eqref{eq:lim4b})}\\ |x-1|\cdot |x^2+x-1| &< \epsilon\\ |x^3-2x+1| &< \epsilon\\ |(x^3-2x)-(-1)| &<\epsilon, \end{align*}\]
це те, що ми хотіли показати. Таким чином\(\lim\limits_{x\to 1}x^3-2x = -1\).
Ми ще раз проілюструємо оцінку лімітів.
Приклад 9: Оцінка ліміту за допомогою визначення
Доведіть, що\(\lim\limits_{x\rightarrow 0} e^x = 1. \)
Рішення
Символічно ми хочемо взяти рівняння\(|e^x - 1| < \epsilon\) і розгадати його до вигляду\(|x-0| < \delta\). Ось наша подряпина—робота:
\[\begin{eqnarray*}|e^x - 1| < \epsilon&\\ -\epsilon < e^x - 1 < \epsilon& \qquad \textrm{(Definition of absolute value)}\\ 1-\epsilon < e^x < 1+\epsilon & \qquad \textrm{(Add 1)}\\ \ln(1-\epsilon) < x < \ln(1+\epsilon) & \qquad \textrm{(Take natural logs)}\\ \end{eqnarray*}\]
Складання безпечного припущення, яке\(\epsilon<1\) забезпечує останню нерівність, є дійсним (тобто таким чином, що\(\ln (1-\epsilon)\) визначено). Потім ми можемо встановити\(\delta\), щоб бути мінімальним\(|\ln(1-\epsilon)|\) і\(\ln(1+\epsilon)\); тобто,
\[\delta = \min\{|\ln(1-\epsilon)|, \ln(1+\epsilon)\} = \ln(1+\epsilon).\]
Згадайте\(\ln 1= 0\) і\(\ln x<0\) коли\(0<x<1\). Отже\(\ln (1-\epsilon) <0\), звідси і розглянемо його абсолютну величину.
Тепер ми працюємо над фактичним доказом:
\[\begin{align*} |x - 0|&<\delta\\ -\delta &< x < \delta & \textrm{(Definition of absolute value)}\\ -\ln(1+\epsilon) &< x < \ln(1+\epsilon). &\\ \ln(1-\epsilon) &< x < \ln(1+\epsilon). & \text{(since \(\ln(1-\epsilon) < -\ln(1+\epsilon)\))}\\ \end{align*}\]
Вищевказана лінія вірна нашим вибором\(\delta\) і тим, що з тих пір\(|\ln(1-\epsilon)|>\ln(1+\epsilon)\) і\(\ln(1-\epsilon)<0\), ми знаємо\(\ln(1-\epsilon) < -\ln(1+\epsilon )\).
\[\begin{align*}1-\epsilon &< e^x < 1+\epsilon & \textrm{(Exponentiate)}\\ -\epsilon &< e^x - 1 < \epsilon & \textrm{(Subtract 1)}\\ \end{align*}\]
Підсумовуючи, дано\(\epsilon > 0\), нехай\(\delta = \ln(1+\epsilon)\). Потім\(|x - 0| < \delta\) має на увазі за\(|e^x - 1|< \epsilon\) бажанням. Ми показали, що\(\displaystyle \lim_{x\rightarrow 0} e^x = 1 .\)
Зауважимо, що ми могли б насправді показати, що\(\lim_{x\rightarrow c} e^x = e^c \) для будь-якої константи\(c\). Ми робимо це факторингом\(e^c\) з обох сторін, залишаючи нас показувати\(\lim_{x\rightarrow c} e^{x-c} = 1 \) замість цього. Використовуючи підміну\(u=x-c\), це зводиться до показу того,\(\lim_{u\rightarrow 0} e^u = 1 \) що ми тільки що зробили в останньому прикладі. Як додаткова перевага, це показує, що насправді функція\(f(x)=e^x\) є безперервною при всіх значеннях\(x\), важливе поняття, яке ми визначимо в Розділі 1.5.
Це формальне визначення межі не є легким поняттям зрозуміти. Наші приклади насправді є «легкими» прикладами, використовуючи «прості» функції, такі як поліноми, квадратні корені та експоненціальні. Дуже складно довести, використовуючи наведені вище прийоми, що\(\lim\limits_{x\to 0}(\sin x)/x = 1\), як ми наблизилися в попередньому розділі.
Є надія. У наступному розділі показано, як можна оцінити складні межі, використовуючи певні базові обмеження як будівельні блоки. Хоча межі є неймовірно важливою частиною обчислення (а отже, і більша частина вищої математики), рідко обмежуються за допомогою визначення. Швидше за все, застосовуються прийоми наступного розділу.
