14.2: Межі та безперервність

Цілі навчання

• Обчислити межу функції двох змінних.
• Дізнайтеся, як функція двох змінних може наближатися до різних значень у граничній точці, залежно від шляху наближення.
• Створіть умови неперервності функції двох змінних.
• Перевірте безперервність функції двох змінних в точці.
• Обчисліть межу функції з трьох або більше змінних і перевірити безперервність функції в точці.

Зараз ми розглянули функції більш ніж однієї змінної і побачили, як їх графікувати. У цьому розділі ми бачимо, як взяти межу функції більш ніж однієї змінної, і що це означає, щоб функція більше однієї змінної була безперервною в точці своєї області. Виявляється, ці поняття мають аспекти, які просто не зустрічаються з функціями однієї змінної.

Межа функції двох змінних

Нагадаємо з розділу 2.5, що визначення межі функції однієї змінної:

$f(x)$Дозволяти визначено для всіх$x≠a$ у відкритому інтервалі, що містить$a$. $L$Дозволяти бути дійсним числом. Тоді

$$\lim_{x→a}f(x)=L \nonumber$$

якщо для кожного$ε>0,$ існує такий$δ>0$, що якщо$0<|x−a|<δ$ для всіх$x$ в області$f$, то

$$|f(x)−L|<ε. \nonumber$$

Перш ніж ми зможемо адаптувати це визначення для визначення межі функції двох змінних, ми спочатку повинні побачити, як розширити ідею відкритого інтервалу в одній змінній до відкритого інтервалу в двох змінних.

Визначення:$\delta$ Disks

Розглянемо$(a,b)∈\mathbb{R}^2.$ точку$δ$ Диск, центрований у точці,$(a,b)$ визначається як відкритий диск радіусу,$δ$ центрований у$(a,b)$ точці, тобто

$$\{(x,y)∈\mathbb{R}^2∣(x−a)^2+(y−b)^2<δ^2\} \nonumber$$

як показано на малюнку$\PageIndex{1}$.

Малюнок$\PageIndex{1}$:$δ$ Диск з центром навколо точки$(2,1)$.

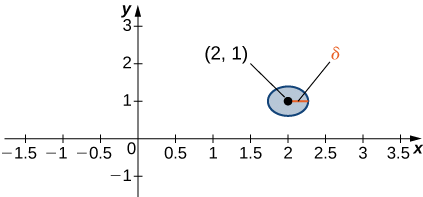
Ідея$δ$ диска з'являється у визначенні межі функції двох змінних. Якщо$δ$ мало, то всі точки$(x,y)$ в$δ$ диску знаходяться близько до$(a,b)$. Це повністю аналогічно тому, що х близький до a у визначенні межі функції однієї змінної. В одному вимірі ми виражаємо це обмеження як

\[a−δ<a+δ.>/span>

У більш ніж одному вимірі ми використовуємо$δ$ диск.

Визначення: межа функції двох змінних

$f$Дозволяти бути функцією двох змінних,$x$ і$y$. Межа$f(x,y)$ як$(x,y)$ підходів$(a,b)$ є$L$, написано

$$\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber$$

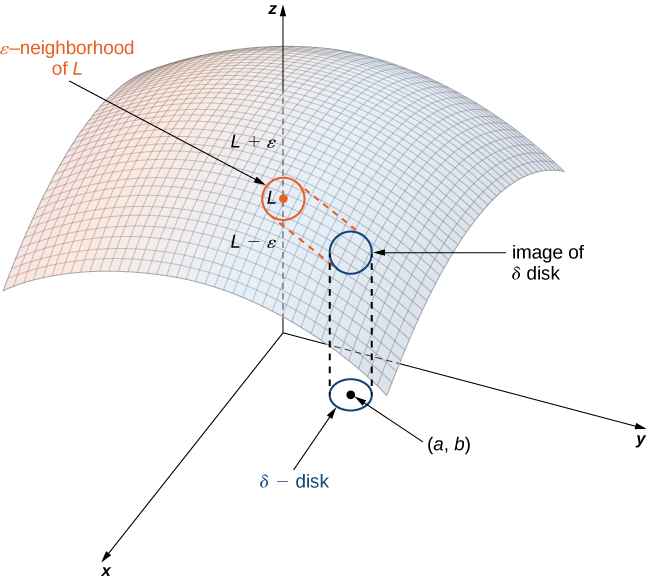
якщо для кожного$ε>0$ існує досить маленька$δ>0$ така, що для всіх точок$(x,y)$ в$δ$ диску навколо$(a,b)$, крім можливо для$(a,b)$ себе, значення$f(x,y)$ не більше ніж$ε$ далеко від$L$ (рис.$\PageIndex{2}$).

Використовуючи символи, пишемо наступне: Для будь-якого$ε>0$ існує число$δ>0$ таке, що

$$|f(x,y)−L|<ε \nonumber$$

щоразу

$$0<\sqrt{(x−a)^2+(y−b)^2}<δ. \nonumber$$

Малюнок$\PageIndex{2}$: Межа функції, що включає дві змінні, вимагає, щоб$f(x,y)$ бути всередині$ε$ кожного$L$ разу, коли$(x,y)$ знаходиться в межах$δ$$(a,b)$. Чим менше значення$ε$, тим менше значення$δ$.

Доведення того, що межа існує за допомогою визначення межі функції двох змінних може бути складним завданням. Замість цього ми використовуємо наступну теорему, яка дає нам ярлики для пошуку меж. Формули в цій теоремі є продовженням формул в теоремі граничних законів в «Граничних законі».

Граничні закони для функцій двох змінних

Нехай$f(x,y)$ і$g(x,y)$ буде визначено для всіх$(x,y)≠(a,b)$ в околицях навколо$(a,b)$, і припустимо, що околиці містяться повністю всередині області$f$. Припустимо, що$L$ і$M$ є дійсними числами такі, що

$$\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber$$

і

$$\lim_{(x,y)→(a,b)}g(x,y)=M, \nonumber$$

і нехай$c$ буде постійною. Тоді кожне з наступних тверджень тримає:

Постійний закон:

$$\lim_{(x,y)→(a,b)}c=c \nonumber$$

Закони ідентичності:

$$\lim_{(x,y)→(a,b)}x=a \nonumber$$

$$\lim_{(x,y)→(a,b)}y=b \nonumber$$

Закон про суму:

$$\lim_{(x,y)→(a,b)}(f(x,y)+g(x,y))=L+M \nonumber$$

Закон різниці:

$$\lim_{(x,y)→(a,b)}(f(x,y)−g(x,y))=L−M \nonumber$$

Постійний множинний закон:

$$\lim_{(x,y)→(a,b)}(cf(x,y))=cL \nonumber$$

Закон про продукт:

$$\lim_{(x,y)→(a,b)}(f(x,y)g(x,y))=LM \nonumber$$

Коефіцієнтне право:

$$\lim_{(x,y)→(a,b)}\dfrac{f(x,y)}{g(x,y)}=\dfrac{L}{M} \text{ for } M≠0 \nonumber$$

Закон про владу:

$$\lim_{(x,y)→(a,b)}(f(x,y))^n=L^n \nonumber$$

для будь-якого натурального цілого числа$n$.

Кореневий закон:

$$\lim_{(x,y)→(a,b)}\sqrt[n]{f(x,y)}=\sqrt[n]{L} \nonumber$$

для всіх$L$ якщо$n$ непарний і позитивний, а для$L≥0$ якщо n парний і позитивний.

Докази цих властивостей аналогічні таким для меж функцій однієї змінної. Ми можемо застосувати ці закони для знаходження меж різних функцій.

Приклад$\PageIndex{1}$: Finding the Limit of a Function of Two Variables

Знайдіть кожне з наступних обмежень:

1. $\displaystyle \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6)$
2. $\displaystyle \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y}$

Рішення

а. спочатку використовуйте закони суми та різниці, щоб розділити терміни:

$$\begin{align*} \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6)\\ = \left(\lim_{(x,y)→(2,−1)}x^2 \right)− \left(\lim_{(x,y)→(2,−1)}2xy \right)+ \left(\lim_{(x,y)→(2,−1)}3y^2 \right)−\left(\lim_{(x,y)→(2,−1)}4x\right) \\ + \left(\lim_{(x,y)→(2,−1)}3y \right)−\left(\lim_{(x,y)→(2,−1)}6\right). \end{align*}$$

Далі використовуйте постійний кратний закон на другому, третьому, четвертому і п'ятому межах:

$$\begin{align*} =(\lim_{(x,y)→(2,−1)}x^2)−2(\lim_{(x,y)→(2,−1)}xy)+3(\lim_{(x,y)→(2,−1)}y^2)−4(\lim_{(x,y)→(2,−1)}x) \\[4pt] +3(\lim_{(x,y)→(2,−1)}y)−\lim_{(x,y)→(2,−1)}6.\end{align*}$$

Тепер скористайтеся законом влади на першому і третьому лімітах, а товарний закон про другу межу:

$$\begin{align*} \left(\lim_{(x,y)→(2,−1)}x\right)^2−2\left(\lim_{(x,y)→(2,−1)}x\right) \left(\lim_{(x,y)→(2,−1)}y\right)+3\left(\lim_{(x,y)→(2,−1)}y\right)^2 \\ −4\left(\lim_{(x,y)→(2,−1)}x\right)+3\left(\lim_{(x,y)→(2,−1)}y\right)−\lim_{(x,y)→(2,−1)}6. \end{align*}$$

Останній, використовуйте закони ідентичності на перших шести лімітах і постійний закон про останню межу:

$$\begin{align*} \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6) = (2)^2−2(2)(−1)+3(−1)^2−4(2)+3(−1)−6 \\[4pt] =−6. \end{align*}$$

б. перш ніж застосовувати закон частки, нам потрібно переконатися, що межа знаменника ненульова. Використовуючи закон різниці, постійний множинний закон та закон ідентичності,

$$\begin{align*} \lim_{(x,y)→(2,−1)}(4x−3y) =\lim_{(x,y)→(2,−1)}4x−\lim_{(x,y)→(2,−1)}3y \\[4pt] =4(\lim_{(x,y)→(2,−1)}x)−3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =4(2)−3(−1)=11. \end{align*}$$

Так як межа знаменника ненульова, застосовується часткове право. Тепер обчислюємо межу чисельника, використовуючи закон різниці, постійний кратний закон та закон ідентичності:

$$\begin{align*} \lim_{(x,y)→(2,−1)}(2x+3y) =\lim_{(x,y)→(2,−1)}2x+\lim_{(x,y)→(2,−1)}3y \\[4pt] =2(\lim_{(x,y)→(2,−1)}x)+3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =2(2)+3(−1)=1. \end{align*}$$

Тому відповідно до актоіентного закону ми маємо

$$\begin{align*} \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y} =\dfrac{\displaystyle \lim_{(x,y)→(2,−1)}(2x+3y)}{\displaystyle \lim_{(x,y)→(2,−1)}(4x−3y)} \\[4pt] =\dfrac{1}{11}. \end{align*}$$

Вправа$\PageIndex{1}$:

Оцініть наступний ліміт:

$$\lim_{(x,y)→(5,−2)}\sqrt[3]{\dfrac{x^2−y}{y^2+x−1}}. \nonumber$$

Підказка

Використовуйте граничні закони.

Відповідь

$$\displaystyle \lim_{(x,y)→(5,−2)}\sqrt[3]{\dfrac{x^2−y}{y^2+x−1}}=\dfrac{3}{2} \nonumber$$

Оскільки ми беремо межу функції двох змінних, точка$(a,b)$ знаходиться в$\mathbb{R}^2$, і можна наблизитися до цієї точки з нескінченної кількості напрямків. Іноді при обчисленні ліміту відповідь змінюється в залежності від шляху, прийнятого назустріч$(a,b)$. Якщо це так, то межа не існує. Іншими словами, межа повинна бути унікальною, незалежно від пройденого шляху.

Приклад$\PageIndex{2}$: Limits That Fail to Exist

Показати, що жодна з таких обмежень не існує:

1. $\displaystyle \lim_{(x,y)→(0,0)}\dfrac{2xy}{3x^2+y^2}$
2. $\displaystyle \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4}$

Рішення

а Область функції$f(x,y)=\dfrac{2xy}{3x^2+y^2}$ складається з усіх точок на$xy$ -площині, крім точки$(0,0)$ (рис.$\PageIndex{3}$). Щоб показати, що межа не існує як$(x,y)$ підходи$(0,0)$, відзначимо, що неможливо задовольнити визначення межі функції двох змінних через те, що функція приймає різні значення по різних лініях, що проходять через точку$(0,0)$. Спочатку розглянемо лінію$y=0$ в$xy$ -площині. Підставляючи$y=0$ в$f(x,y)$ дає

$$f(x,0)=\dfrac{2x(0)}{3x^2+0^2}=0 \nonumber$$

за будь-яке значення$x$. Тому значення$f$ залишається постійним для будь-якої точки на$x$ -осі, а при$y$ наближенні до нуля функція залишається фіксованою на нулі.

Далі розглянемо рядок$y=x$. Підставляючи$y=x$ в$f(x,y)$ дає

$$f(x,x)=\dfrac{2x(x)}{3x^2+x^2}=\dfrac{2x^2}{4x^2}=\tfrac{1}{2}. \nonumber$$

Це справедливо для будь-якої точки на лінії$y=x$. Якщо ми дозволимо$x$ наблизитися до нуля, залишаючись на цьому рядку, значення функції залишається фіксованим на$\tfrac{1}{2}$, незалежно від того, наскільки малим$x$ є.

Виберіть значення для ε, яке менше, ніж$1/2$ —скажімо,$1/4$. Тоді, незалежно від того, наскільки маленький$δ$ диск ми малюємо навколо$(0,0)$, значення$f(x,y)$ для точок всередині цього$δ$ диска буде включати обидва$0$ і$\tfrac{1}{2}$. Тому визначення межі в точці ніколи не задовольняється, і межа не існує.

Малюнок$\PageIndex{3}$: Графік функції$f(x,y)=\dfrac{2xy}{3x^2+y^2}.$ Уздовж лінії$y=0$ функція дорівнює нулю;$y=x$ по лінії функція дорівнює$\tfrac{1}{2}$.

б Подібним чином до а., ми можемо наблизитися до початку по будь-якій прямій лінії, що проходить через початок. Якщо ми спробуємо$x$ -axis (тобто$y=0$), то функція залишається фіксованою на нулі. Те ж саме справедливо і для$y$ -осі. Припустимо, ми наближаємося до початку по прямій лінії ухилу$k$. Рівняння цієї лінії є$y=kx$. Тоді межа стає

$$\begin{align*} \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} = \lim_{(x,y)→(0,0)}\dfrac{4x(kx)^2}{x^2+3(kx)^4} \\ = \lim_{(x,y)→(0,0)}\dfrac{4k^2x^3}{x^2+3k^4x^4} \\ =\lim_{(x,y)→(0,0)}\dfrac{4k^2x}{1+3k^4x^2} \\ = \dfrac{\displaystyle \lim_{(x,y)→(0,0)}(4k^2x)}{\displaystyle \lim_{(x,y)→(0,0)}(1+3k^4x^2)} \\ = 0. \end{align*}$$

незалежно від величини$k$. Здавалося б, межа дорівнює нулю. Що робити, якщо замість цього ми вибрали криву, що проходить через початок? Для прикладу можна розглянути параболу, задану рівнянням$x=y^2$. $y^2$Заміна замість$x$ in$f(x,y)$ дає

$$\begin{align*}\lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} = \lim_{(x,y)→(0,0)}\dfrac{4(y^2)y^2}{(y^2)^2+3y^4} \\ = \lim_{(x,y)→(0,0)}\dfrac{4y^4}{y^4+3y^4} \\ = \lim_{(x,y)→(0,0)}1 \\ = 1. \end{align*}$$

За тією ж логікою в частині a неможливо знайти δ диск навколо походження, який задовольняє визначенню межі для будь-якого значення$ε<1.$ Тому,

$$\displaystyle \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} \nonumber$$

не існує.

Вправа$\PageIndex{2}$:

Покажіть, що

$$\lim_{(x,y)→(2,1)}\dfrac{(x−2)(y−1)}{(x−2)^2+(y−1)^2} \nonumber$$

не існує.

Підказка

Виберіть лінію з нахилом,$k$ що проходить через точку$(2,1).$

Відповідь

Якщо$y=k(x−2)+1,$ тоді$\lim_{(x,y)→(2,1)}\dfrac{(x−2)(y−1)}{(x−2)^2+(y−1)^2}=\dfrac{k}{1+k^2}$. Так як відповідь залежить від$k,$ ліміту не існує.

Внутрішні точки і граничні точки

Щоб вивчити безперервність і диференційовність функції двох або більше змінних, спочатку потрібно вивчити нову термінологію.

Визначення: внутрішні та граничні точки

$S$Дозволяти бути підмножиною$\mathbb{R}^2$ (Рисунок$\PageIndex{4}$).

1. Точка$P_0$ називається внутрішньою точкою,$S$ якщо є$δ$ диск з центром навколо$P_0$ міститься повністю в$S$.
2. Точка$P_0$ називається крайовою точкою,$S$ якщо кожен$δ$ диск, центрований навколо,$P_0$ містить точки як всередині, так і зовні$S$.

Рисунок$\PageIndex{4}$: У$S$ показаному множині$(−1,1)$ є внутрішньою точкою та$(2,3)$ крайовою точкою.

Визначення: Відкриті та закриті множини

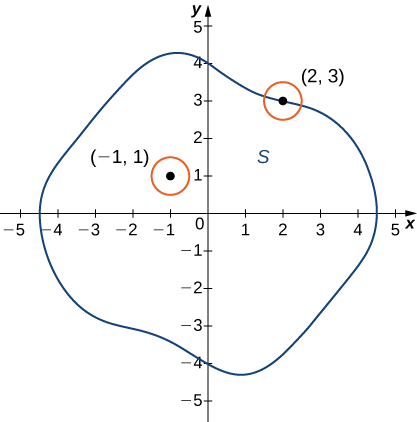
$S$Дозволяти бути підмножиною$\mathbb{R}^2$ (Рисунок$\PageIndex{4}$).

1. $S$називається відкритим набором, якщо кожна точка$S$ є внутрішньою точкою.
2. $S$називається замкнутою множиною, якщо вона містить всі його граничні точки.

Прикладом відкритого набору є$δ$ диск. Якщо включити межу диска, то він стає замкнутим набором. Набір, який містить деякі, але не всі його граничні точки, не є ні відкритими, ні закритими. Наприклад, якщо ми включимо половину межі$δ$ диска, але не іншу половину, то набір не є ні відкритим, ні закритим.

Визначення: з'єднані множини та регіони

$S$Дозволяти бути підмножиною$\mathbb{R}^2$ (Рисунок$\PageIndex{4}$).

1. Відкрита$S$ множина є зв'язаною множиною, якщо вона не може бути представлена як об'єднання двох або більше непорожніх відкритих підмножин.
2. Набір$S$ — це область, якщо вона відкрита, підключена та непорожня.

Визначення межі функції двох змінних вимагає, щоб$δ$ диск містився всередині області функції. Однак, якщо ми хочемо знайти межу функції в граничній точці домену,$δ$ диск не міститься всередині домену. За визначенням, деякі точки$δ$ диска знаходяться всередині домену, а деякі - зовні. Тому нам потрібно тільки розглядати точки, які знаходяться всередині і$δ$ диска, і області функції. Це призводить до визначення межі функції в граничній точці.

Визначення

$f$Дозволяти бути функція двох змінних$y$,$x$ і, і припустимо$(a,b)$ знаходиться на межі області$f$. Потім межа$f(x,y)$ як$(x,y)$ підходів$(a,b)$$L$, написано

$$\lim_{(x,y)→(a,b)}f(x,y)=L, \nonumber$$

якщо для будь-якого$ε>0,$ існує$δ>0$ таке число, що для будь-якої точки$(x,y)$ всередині області$f$ і в межах відповідної невеликої відстані$δ$ додатне значення$f(x,y)$ не більше ніж$ε$ далеко від$L$ (рис.$\PageIndex{2}$).$(a,b),$ Використовуючи символи, ми можемо написати: Для будь-якого$ε>0$ існує$δ>0$ таке число, що

$$|f(x,y)−L|<ε\, \text{whenever}\, 0<\sqrt{(x−a)^2+(y−b)^2}<δ. \nonumber$$

Приклад$\PageIndex{3}$: Limit of a Function at a Boundary Point

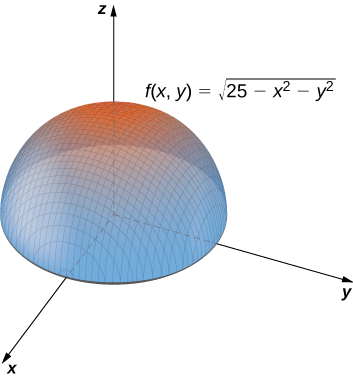
Довести

$$\lim_{(x,y)→(4,3)}\sqrt{25−x^2−y^2}=0. \nonumber$$

Рішення

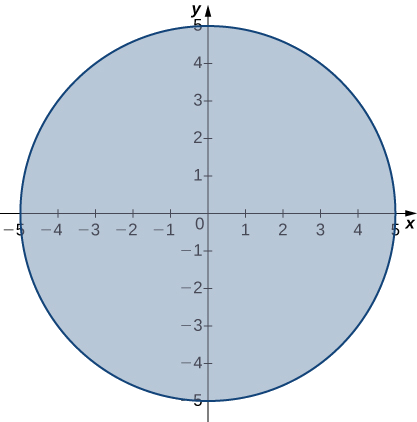
Домен функції$f(x,y)=\sqrt{25−x^2−y^2}$ - це коло радіуса$\big\{(x,y)∈\mathbb{R}^2∣x^2+y^2≤25\big\}$,$5$ зосереджене на початку, разом з його внутрішньою частиною, як показано на малюнку$\PageIndex{5}$.

Малюнок$\PageIndex{5}$: Домен функції$f(x,y)=\sqrt{25−x^2−y^2}$.

Ми можемо використовувати граничні закони, які застосовуються до лімітів на кордоні доменів, а також внутрішніх точок:

$$\begin{align*} \lim_{(x,y)→(4,3)}\sqrt{25−x^2−y^2} =\sqrt{\lim_{(x,y)→(4,3)}(25−x^2−y^2)} \\ = \sqrt{\lim_{(x,y)→(4,3)}25−\lim_{(x,y)→(4,3)}x^2−\lim_{(x,y)→(4,3)}y^2} \\ =\sqrt{25−4^2−3^2} \\ = 0 \end{align*}$$

Див. Наступний графік.

Малюнок$\PageIndex{6}$: Графік функції$f(x,y)=\sqrt{25−x^2−y^2}$.

Вправа$\PageIndex{3}$

Оцініть наступний ліміт:

$$\lim_{(x,y)→(5,−2)}\sqrt{29−x^2−y^2}. \nonumber$$

Підказка

Визначте домен домену$f(x,y)=\sqrt{29−x^2−y^2}$.

Відповідь

$$\lim_{(x,y)→(5,−2)}\sqrt{29−x^2−y^2} \nonumber$$

Неперервність функцій двох змінних

У Continuity ми визначили неперервність функції однієї змінної і побачили, як вона спирається на межу функції однієї змінної. Зокрема, три умови необхідні для$f(x)$ того, щоб бути безперервним у точці$x=a$

1. $f(a)$існує.
2. $\displaystyle \lim_{x→a}f(x)$існує.
3. $\displaystyle \lim_{x→a}f(x)=f(a).$

Ці три умови необхідні і для неперервності функції двох змінних.

Визначення: безперервні функції

Функція$f(x,y)$ є безперервною$(a,b)$ в точці своєї області, якщо виконуються такі умови:

1. $f(a,b)$існує.
2. $\displaystyle \lim_{(x,y)→(a,b)}f(x,y)$існує.
3. $\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).$

Приклад$\PageIndex{4}$: Demonstrating Continuity for a Function of Two Variables

Показати, що функція

$$f(x,y)=\dfrac{3x+2y}{x+y+1} \nonumber$$

безперервний в точці$(5,−3).$

Рішення

Існує три умови, які слід задовольнити, відповідно до визначення безперервності. У цьому прикладі$a=5$ і$b=−3.$

1. $f(a,b)$існує. Це вірно тому, що область функції f складається з тих впорядкованих пар, для яких знаменник ненульовий (тобто$x+y+1≠0$). Точка$(5,−3)$ задовольняє цій умові. Крім того,

$$f(a,b)=f(5,−3)=\dfrac{3(5)+2(−3)}{5+(−3)+1}=\dfrac{15−6}{2+1}=3. \nonumber$$

2. $\displaystyle \lim_{(x,y)→(a,b)}f(x,y)$існує. Це також вірно:

$$\begin{align*} \lim_{(x,y)→(a,b)}f(x,y) =\lim_{(x,y)→(5,−3)}\dfrac{3x+2y}{x+y+1} \\ =\dfrac{\displaystyle \lim_{(x,y)→(5,−3)}(3x+2y)}{\displaystyle \lim_{(x,y)→(5,−3)}(x+y+1)} \\ = \dfrac{15−6}{5−3+1} \\ = 3. \end{align*}$$

3. $\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).$Це правда, тому що ми щойно показали, що обидві сторони цього рівняння дорівнюють трьом.

Вправа$\PageIndex{4}$

Показати, що функція

$$f(x,y)=\sqrt{26−2x^2−y^2}\nonumber$$

безперервний в точці$(2,−3)$.

Підказка

Використовуйте тричасткове визначення безперервності.

Відповідь

1. Домен$f$ містить впорядковану пару$(2,−3)$, оскільки$f(a,b)=f(2,−3)=\sqrt{16−2(2)^2−(−3)^2}=3$
2. $\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=3$
3. $\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b)=3$

Неперервність функції будь-якої кількості змінних також може бути визначена через дельта та епсилон. Функція двох змінних є безперервною$(x_0,y_0)$ в точці своєї області, якщо для кожного$ε>0$ існує$δ>0$ таке, що, коли$\sqrt{(x−x_0)^2+(y−y_0)^2}<δ$ це правда,$|f(x,y)−f(a,b)|<ε.$ Це визначення може бути об'єднано з формальним визначенням (тобто епсилон - дельта визначення) безперервності функції однієї змінної для доведення наступних теорем:

Сума неперервних функцій неперервна

Якщо$f(x,y)$ безперервний при$(x_0,y_0)$, і$g(x,y)$ безперервний при$(x_0,y_0)$,$f(x,y)+g(x,y)$ то безперервний при$(x_0,y_0)$.

Добуток безперервних функцій є безперервним

Якщо$g(x)$ безперервний при$x_0$ і$h(y)$ безперервний при$y_0$,$f(x,y)=g(x)h(y)$ то безперервний при$(x_0,y_0).$

Склад неперервних функцій є безперервним

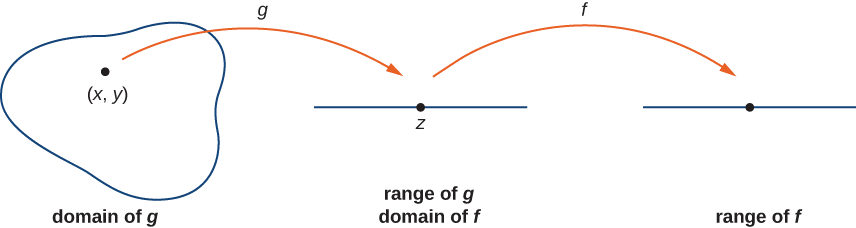
$g$Дозволяти бути функція двох змінних від області$D⊆\mathbb{R}^2$ до діапазону$R⊆R.$ Припустимо$g$ є безперервним в якийсь момент$(x_0,y_0)∈D$ і визначити$z_0=g(x_0,y_0)$. Дозволяти f бути функція, яка$R$$R$ відображає такі, що$z_0$ знаходиться в області$f$. Останній, припустимо,$f$ є безперервним в$z_0$. Потім$f∘g$ безперервно при$(x_0,y_0)$, як показано на малюнку$\PageIndex{7}$.

Малюнок$\PageIndex{7}$: Склад двох неперервних функцій є безперервним.

Давайте тепер використаємо попередні теореми, щоб показати неперервність функцій у наступних прикладах.

Приклад$\PageIndex{5}$: More Examples of Continuity of a Function of Two Variables

Покажіть, що функції$f(x,y)=4x^3y^2$ і$g(x,y)=\cos(4x^3y^2)$ є безперервними всюди.

Рішення

$h(y)=y^2$Поліноми$g(x)=4x^3$ і є неперервними в кожному дійсному числі, а отже, за добутком теореми неперервних функцій,$f(x,y)=4x^3y^2$ є неперервними$(x,y)$ в кожній точці$xy$ -площині. Оскільки$f(x,y)=4x^3y^2$ є безперервним у кожній точці$(x,y)$$xy$ -площині і$g(x)=\cos x$ є безперервним у кожному дійсному числі$x$, безперервність складу функцій говорить нам, що$g(x,y)=\cos(4x^3y^2)$ є безперервним у кожній точці$(x,y)$ в$xy$ -площині.

Вправа$\PageIndex{5}$

Покажіть, що функції$f(x,y)=2x^2y^3+3$ і$g(x,y)=(2x^2y^3+3)^4$ є безперервними всюди.

Підказка

Використовуйте неперервність суми, добутку та складу двох функцій.

Відповідь

$h(y)=y^3$Поліноми$g(x)=2x^2$ і є неперервними в кожному дійсному числі; отже, за добутком теореми неперервних функцій,$f(x,y)=2x^2y^3$ є безперервним$(x,y)$ у кожній точці$xy$ -площини. Крім того, будь-яка постійна функція є безперервною скрізь,$g(x,y)=3$ тому безперервна в кожній точці$(x,y)$ в$xy$ -площині. Тому$f(x,y)=2x^2y^3+3$ є безперервним у кожній$(x,y)$ точці на$xy$ -площині. Останній,$h(x)=x^4$ є неперервним у кожному дійсному числі$x$, тому за неперервністю композитних функцій теорема$g(x,y)=(2x^2y^3+3)^4$ є безперервною$(x,y)$ в кожній точці$xy$ -площині.

Функції трьох і більше змінних

Межа функції трьох або більше змінних відбувається легко в додатках. Наприклад, припустимо, що у нас є функція$f(x,y,z)$, яка дає температуру у фізичному місці$(x,y,z)$ в трьох вимірах. Або, можливо, функція$g(x,y,z,t)$ може вказувати тиск повітря в певному місці$(x,y,z)$ в той час$t$. Як ми можемо взяти ліміт в точці$\mathbb{R}^3$? Що означає бути безперервним у точці в чотирьох вимірах?

Відповіді на ці питання спираються на розширення поняття$δ$ диска більш ніж на два виміри. Тоді ідеї межі функції трьох і більше змінних і безперервності функції трьох і більше змінних дуже схожі на визначення, наведені раніше для функції двох змінних.

Визначення:$δ$-balls

$(x_0,y_0,z_0)$Дозволяти бути точкою в$\mathbb{R}^3$. Потім$δ$ -куля в трьох вимірах складається з усіх точок$\mathbb{R}^3$ лежачи на відстані менше, ніж$δ$ від$(x_0,y_0,z_0)$ —тобто

$$\big\{(x,y,z)∈\mathbb{R}^3∣\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}<δ\big\}. \nonumber$$

Щоб визначити$δ$ -куля у вищих розмірах, додайте додаткові терміни під радикалом, щоб відповідати кожному додатковому виміру. Наприклад, з огляду на точку$P=(w_0,x_0,y_0,z_0)$ в$\mathbb{R}^4$,$δ$ куля навколо$P$ може бути описаний

$$\big\{(w,x,y,z)∈\mathbb{R}^4∣\sqrt{(w−w_0)^2+(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}<δ\big\}. \nonumber$$

Щоб показати, що межа функції трьох змінних існує в точці$(x_0,y_0,z_0)$, достатньо показати$(x_0,y_0,z_0)$, що для будь-якої точки$δ$ кулі з центром значення функції в цій точці довільно близьке до фіксованого значення (граничне значення). Усі граничні закони для функцій двох змінних мають також функції більше двох змінних.

Приклад$\PageIndex{6}$: Finding the Limit of a Function of Three Variables

Знайти

$$\lim_{(x,y,z)→(4,1,−3)}\dfrac{x^2y−3z}{2x+5y−z}. \nonumber$$

Рішення

Перш ніж ми можемо застосувати закон частки, нам потрібно переконатися, що межа знаменника ненульова. Використовуючи закон різниці, закон ідентичності та постійний закон,

$$\begin{align*}\lim_{(x,y,z)→(4,1,−3)}(2x+5y−z) =2(\lim_{(x,y,z)→(4,1,−3)}x)+5(\lim_{(x,y,z)→(4,1,−3)}y)−(\lim_{(x,y,z)→(4,1,−3)}z) \\ = 2(4)+5(1)−(−3) \\ = 16. \end{align*}$$

Так як це ненульове значення, то далі знаходимо межу чисельника. Використовуючи закон про продукт, закон влади, закон різниці, постійний множинний закон та закон ідентичності,

$$\begin{align*} \lim_{(x,y,z)→(4,1,−3)}(x^2y−3z) =(\lim_{(x,y,z)→(4,1,−3)}x)^2(\lim_{(x,y,z)→(4,1,−3)}y)−3\lim_{(x,y,z)→(4,1,−3)}z \\ =(4^2)(1)−3(−3) \\ = 16+9 \\ = 25 \end{align*}$$

Останній, застосовуючи частковий закон:

$$\lim_{(x,y,z)→(4,1,−3)}\dfrac{x^2y−3z}{2x+5y−z}=\dfrac{\displaystyle \lim_{(x,y,z)→(4,1,−3)}(x^2y−3z)}{\displaystyle \lim_{(x,y,z)→(4,1,−3)}(2x+5y−z)}=\dfrac{25}{16} \nonumber$$

Вправа$\PageIndex{6}$

Знайти

$$\lim_{(x,y,z)→(4,−1,3)}\sqrt{13−x^2−2y^2+z^2} \nonumber$$

Підказка

Використовуйте граничні закони і безперервність складу функцій.

Відповідь

$$\lim_{(x,y,z)→(4,−1,3)}\sqrt{13−x^2−2y^2+z^2}=2 \nonumber$$

Ключові концепції

• Для вивчення обмежень і неперервності функцій двох змінних ми використовуємо$δ$ диск з центром навколо заданої точки.
• Функція декількох змінних має межу, якщо для будь-якої точки$δ$ кулі з центром у$P$ точці значення функції в цій точці довільно близьке до фіксованого значення (граничного значення).
• Граничні закони, встановлені для функції однієї змінної, мають природні розширення функцій більш ніж однієї змінної.
• Функція двох змінних є безперервною в точці, якщо межа існує в цій точці, функція існує в цій точці, а межа і функція рівні в цій точці.

Глосарій

гранична точка

точка$R$ є$P_0$ крайовою точкою, якщо кожен$δ$ диск, центрований навколо,$P_0$ містить точки як всередині, так і зовні$R$

закритий набір

множина$S$, яка містить усі його граничні точки

підключений набір

відкритий набір$S$, який не може бути представлений як об'єднання двох або більше нероз'єднаних, непорожніх відкритих підмножин

$δ$диск

відкритий диск радіуса з$δ$ центром у точці$(a,b)$

$δ$м'яч

всі точки$\mathbb{R}^3$ лежачи на відстані менше, ніж$δ$ від$(x_0,y_0,z_0)$

внутрішня точка

точка$P_0$$\mathbb{R}$ є граничною точкою, якщо є$δ$ диск, зосереджений навколо, повністю$P_0$ міститься в$\mathbb{R}$

відкритий набір

множина$S$, яка не містить жодної з його граничних точок

область

відкрита, підключена, непорожня підмножина$\mathbb{R}^2$