1.1: Вступ до обмежень

Last updated
Save as PDF

Page ID: 60797

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми починаємо наше вивчення обмежень з розгляду прикладів, які демонструють ключові поняття, які будуть пояснюватися в міру просування.

Розглянемо функцію$y = \frac{\sin x}{x}$. Коли$x$ близько значення 1, яке значення (якщо є)$y$ поруч?

Поки наше питання точно не сформовано (що являє собою «біля значення 1»?) , Відповідь не здається складним для пошуку. Можна подумати спочатку подивитися на графік цієї функції, щоб наблизити відповідні$y$ значення.

Розглянемо Малюнок 1, де$y = \frac{\sin x}{x}$ зображено графіки. Для значень$x$ близько 1, здається, що$y$ набуває значень поруч$0.85$. Насправді, коли$x=1$, то$y=\frac{\sin 1}{1} \approx 0.84$, так має сенс,$x$ що коли «поруч» 1,$y$ буде «поруч»$0.84$.

$альт$
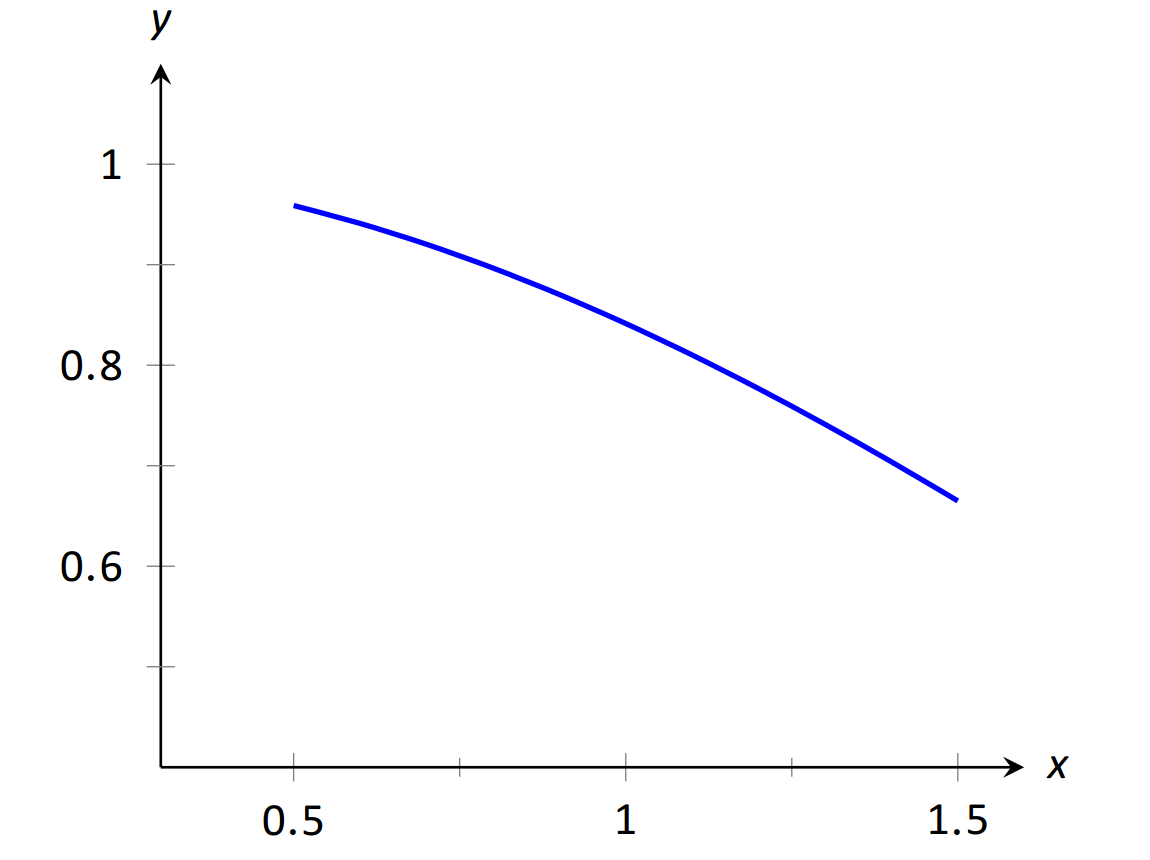
$\text{FIGURE 1.1}$:$\sin (x)/x \text{ near }x=1.$

Розглянемо це ще раз при іншому значенні для$x$. Коли$x$ близько 0, яке значення (якщо є)$y$ поруч? Розглядаючи рисунок 1.2, можна побачити, що здається, що$y$ набуває значень поруч$1$. Але що відбувається, коли$x=0$? У нас є

\[y \rightarrow \frac{\sin 0}{0}\rightarrow "\frac{0}{0}".\nonumber\]

$альт$
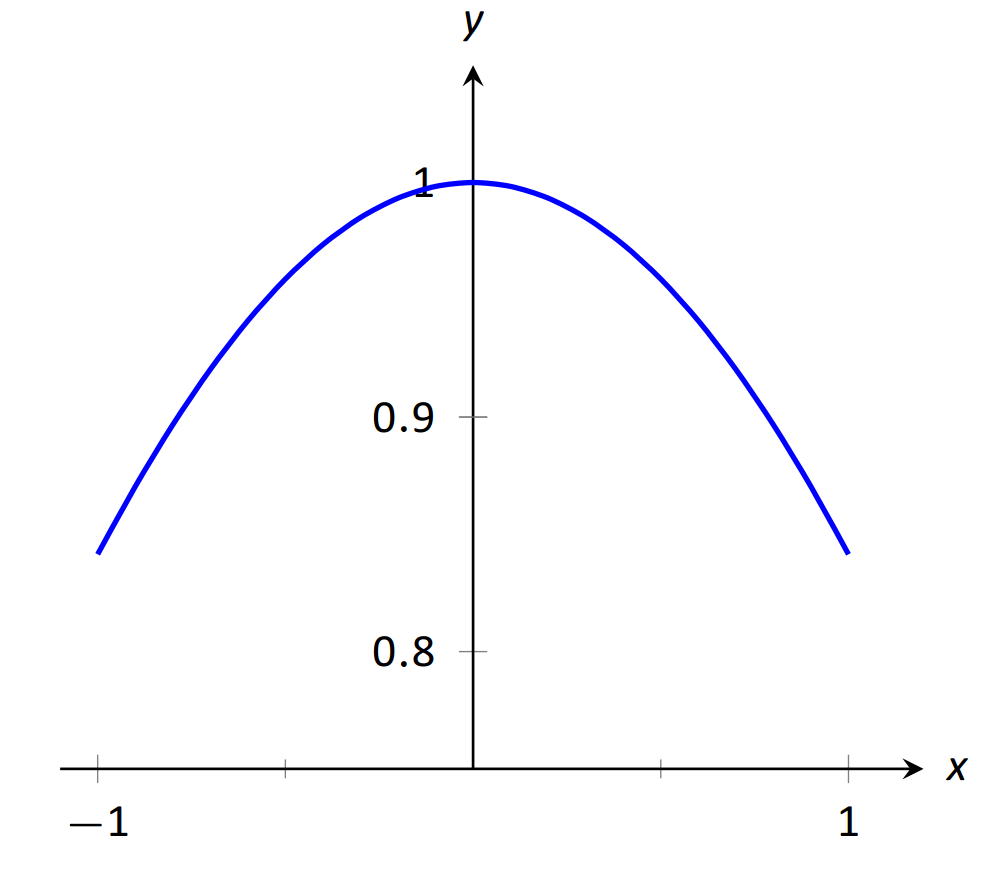
$\text{FIGURE 1.2}$:$\sin (x)/x \text{ near }x=0.$

Вираз "$0/0$" не має значення; воно невизначене. Такий вираз не дає ніякої інформації про те, що відбувається з функцією поруч. Ми не можемо з'ясувати, як$y$ поводиться поблизу$x=0$ цієї функції, просто дозволивши$x=0$.

Пошук межі тягне за собою розуміння того, як функція поводиться поблизу певного значення$x$. Перш ніж продовжити, корисно буде встановити деякі позначення. Дозволяти$y=f(x)$; тобто нехай$y$ бути функцією$x$ для якоїсь функції$f$. Вираз «$y$межа як$x$ наближається 1» описує число, часто називають$L$, що$y$ наближається$x$ до 1. Пишемо все це як

\[\lim_{x\to 1} y = \lim_{x\to 1} f(x) = L.\nonumber\]

Це не повне визначення (яке прийде в наступному розділі); це псевдовизначення, яке дозволить нам дослідити ідею обмеження.

Вище, де$f(x) = \sin(x)/x$, ми наближали

\[\lim_{x\to 1} \frac{\sin x}{x} \approx 0.84 \quad \text{ and } \quad \lim_{x\to 0}\frac{\sin x}{x} \approx 1.\nonumber\]

(Ми наблизили ці межі, отже, використовували символ$\approx$ "", оскільки ми працюємо з псевдовизначенням межі, а не з фактичним визначенням.)

Після того, як ми отримаємо справжнє визначення межі, ми знайдемо межі аналітично; тобто саме за допомогою різноманітних математичних інструментів. Наразі ми наблизимо межі як графічно, так і чисельно. Графік функції може забезпечити хороше наближення, хоча часто не дуже точне. Чисельні методи можуть забезпечити більш точне наближення. Ми вже наблизили межі графічно, тому тепер звернемо увагу на числові наближення.

Розглянемо ще раз$\lim_{x\to 1}\sin (x)/x$. Щоб наблизити цю межу чисельно, ми можемо створити таблицю$x$ і$f(x)$ значень, де$x$ знаходиться «поруч» 1. Це робиться на малюнку 1.3.

$альт$
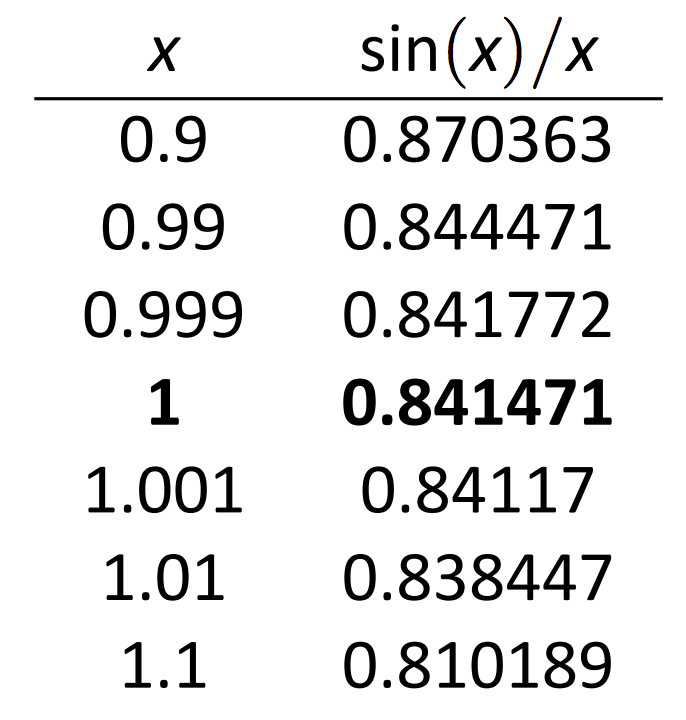
$\text{FIGURE 1.3}$: Значення$\sin (x)/x \text{ with }x \text{ near }1.$

Зверніть увагу, що для значень$x$ поруч$1$, у нас є$\sin (x)/x$ поруч$0.841$. $x=1$Рядок виділений жирним шрифтом, щоб виділити той факт, що при розгляді обмежень, ми не стурбовані значенням функції при цьому конкретному$x$ значенні; ми стурбовані лише значеннями функції, коли$x$ близько 1.

Тепер приблизний$\lim_{x\to 0} \sin(x)/x$ чисельно. Ми вже наблизили значення цієї межі як 1 графічно на малюнку 1.2. У таблиці на малюнку 1.4 показано значення$\sin(x)/x$ для значень$x$ близько 0. Десять знаків після коми показуються, щоб виділити, наскільки близько до 1 значення$\sin(x)/x$ отримує, як$x$ приймає значення дуже близько 0. Ми знову включаємо$x=0$ рядок жирним шрифтом, щоб підкреслити, що ми не стурбовані значенням нашої функції at$x=0$, тільки про поведінку функції біля 0.

$альт$
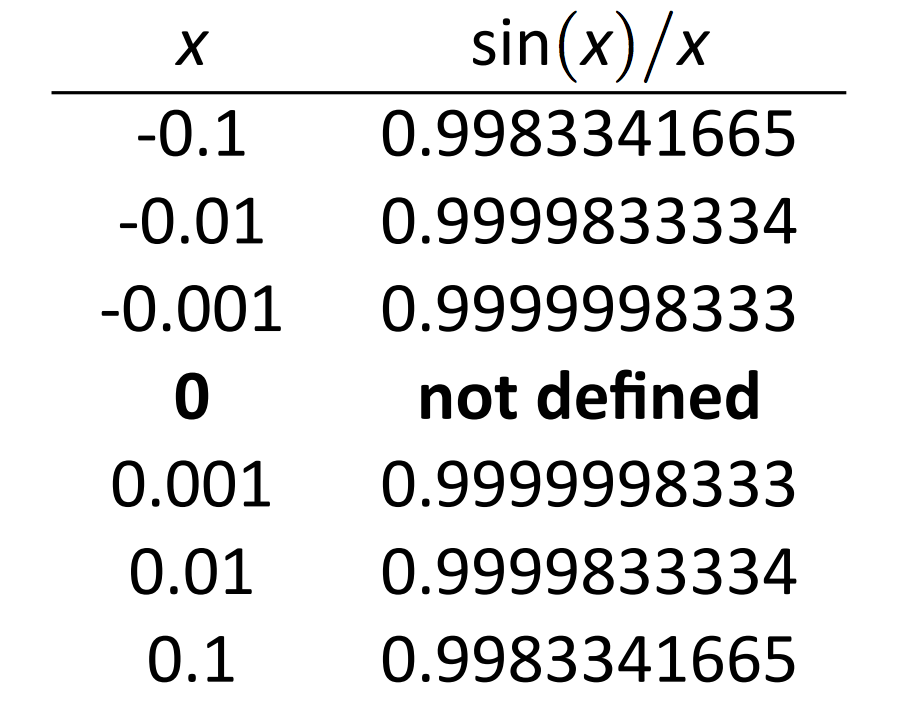
$\text{FIGURE 1.4}$: Значення$\sin (x)/x \text{ with }x \text{ near }1.$

Цей числовий метод дає впевненість сказати, що 1 є хорошим наближенням$\lim_{x\to 0} \sin(x)/x$; тобто

\[\lim_{x\to 0} \sin(x)/x \approx 1.\]

Пізніше ми зможемо довести, що ліміт дорівнює рівно 1.

Зараз ми розглянемо кілька прикладів, які дозволяють досліджувати різні аспекти концепції ліміту.

$альт$
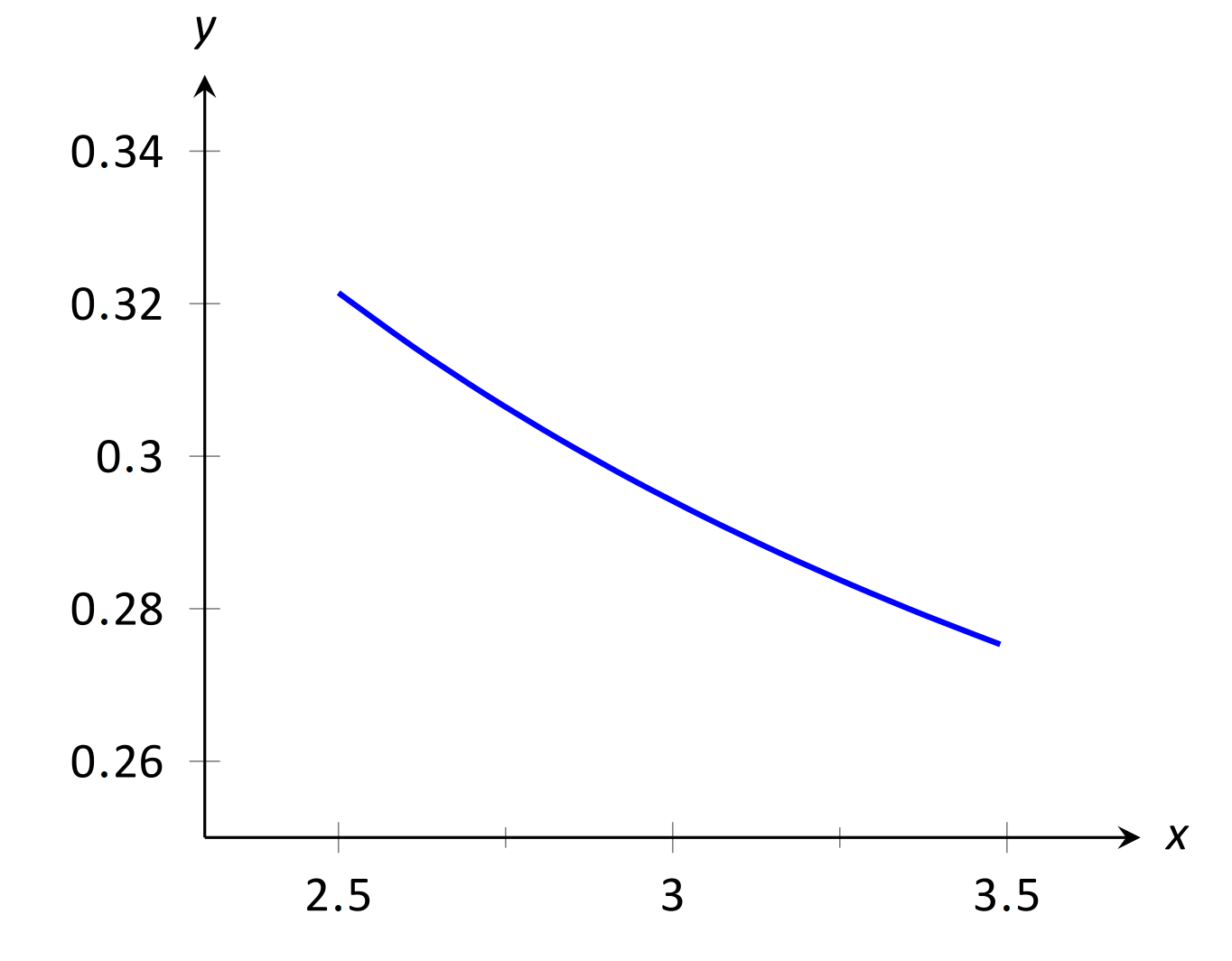
$\text{FIGURE 1.5}$: Графічно наближення межі в прикладі 1.

$альт$
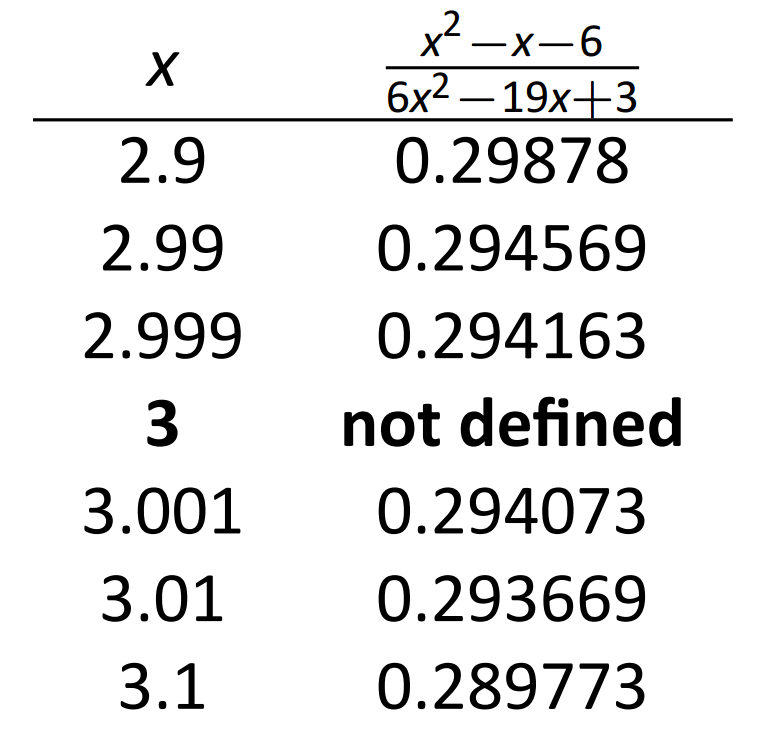
$\text{FIGURE 1.6}$: Числове наближення межі в прикладі 1.

Приклад 1: Наближення значення межі

Використовуйте графічні та числові методи для наближення

\[\lim_{x\to 3} \frac{x^2-x-6}{6x^2-19x+3}.\]

Рішення:
Щоб графічно наблизити межу, графік

\[y = (x^2-x-6)/(6x^2-19x+3)\]

на невеликому інтервалі, який містить 3. Щоб чисельно наблизити межу, створіть таблицю$x$ значень, де значення знаходяться поблизу 3. Це робиться на малюнках 1.5 і 1.6 відповідно.

Графік показує,$x$ що коли близько 3, значення$y$ знаходиться дуже близько$0.3$. Розглядаючи значення$x$ близько 3, ми бачимо, що$y=0.294$ це краще наближення. Графік і таблиця мають на увазі, що

\[\lim_{x\to 3} \frac{x^2-x-6}{6x^2-19x+3} \approx 0.294.\]

Цей приклад може викликати кілька питань про наближення меж (і характер самих меж).

Якщо графік не дає такого хорошого наближення, як таблиця, навіщо з ним турбуватися?
Скільки значень$x$ у таблиці «достатньо»? У попередньому прикладі ми могли б просто використати$x=3.001$ і знайти тонке наближення?

Графіки корисні, оскільки вони дають візуальне розуміння поведінки функції. Іноді функція може діяти «нестабільно» поблизу певних$x$ значень, які важко розрізнити чисельно, але дуже просто графічно. Оскільки графічні утиліти дуже доступні, має сенс правильно їх використовувати.

Оскільки таблиці і графіки використовуються тільки для наближення значення ліміту, немає твердої відповіді на те, скільки точок даних «вистачає». Включіть достатньо, щоб тенденція була зрозумілою, і використовуйте значення (коли це можливо) як менше, так і більше, ніж значення, про яке йде мова. У прикладі 1 ми використовували обидва значення менше і більше 3. Якби ми використовували просто$x=3.001$, ми могли б спокуситися зробити висновок, що межа мала значення$0.3$. Хоча це не за горами, ми могли б зробити краще. Використання значень «по обидва боки 3" допомагає нам визначити тенденції.

Приклад 2: Наближення значення межі

Графічно і чисельно наближається$f(x)$ межа as$x$ наближається до 0, де

\[f(x) = \left \{\begin{array}{rl} x+1 & x< 0 \\ -x^2+1 & x > 0 \end{array}\right . \]

Рішення:
Знову$f(x)$ графуємо і створюємо таблицю її значень поблизу$x=0$ наближеного межі. Зауважте, що це кусково визначена функція, тому вона поводиться по-різному по обидва боки від 0. На малюнку 1.7 показаний графік$f(x)$, і по обидва боки 0 здається, що$y$ значення наближаються до 1. Зверніть увагу,$f(0)$ що насправді не визначено, як зазначено на графіку з відкритим колом.

$альт$
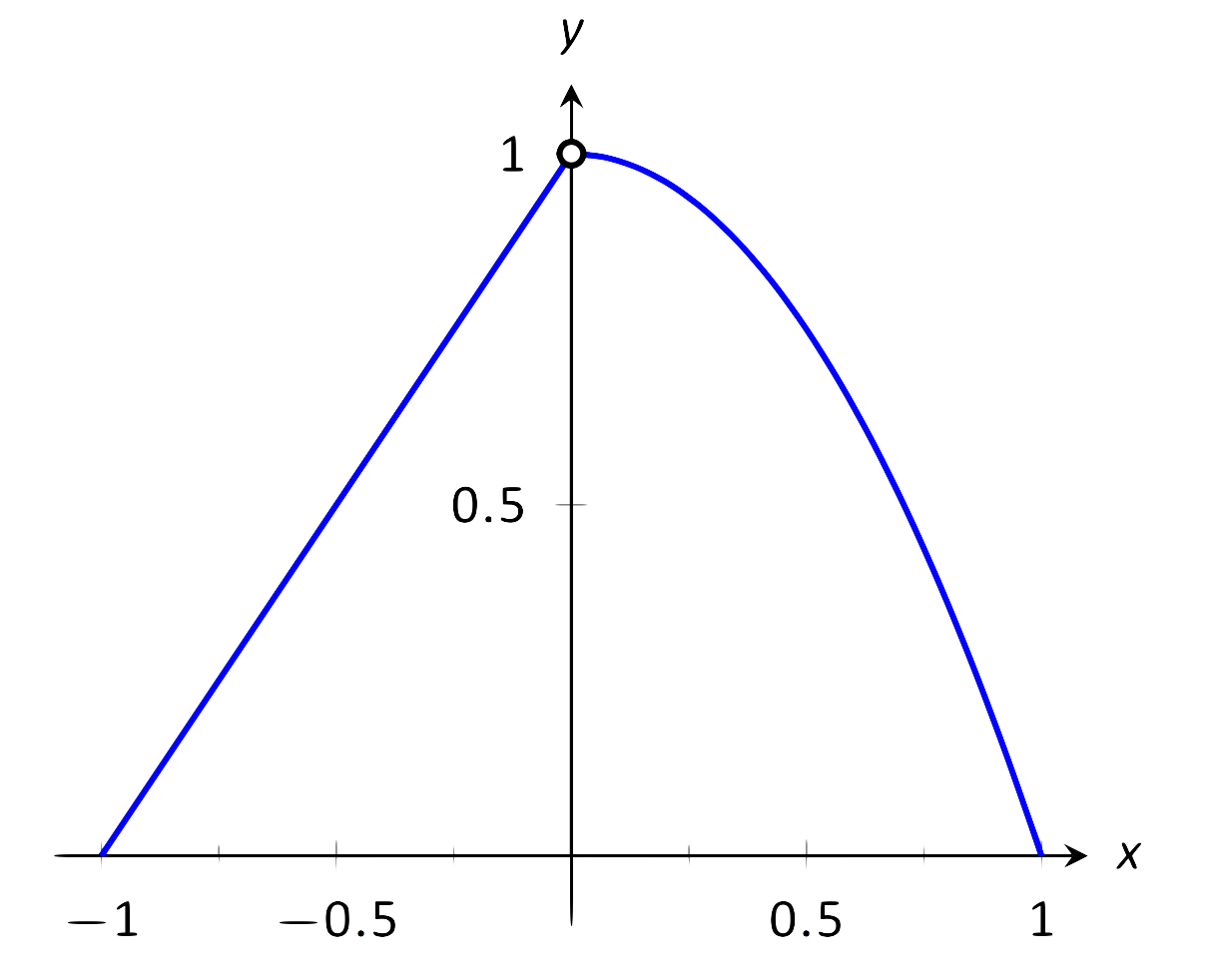
$\text{FIGURE 1.7}$: Графічно наближення межі в прикладі 2.

$альт$
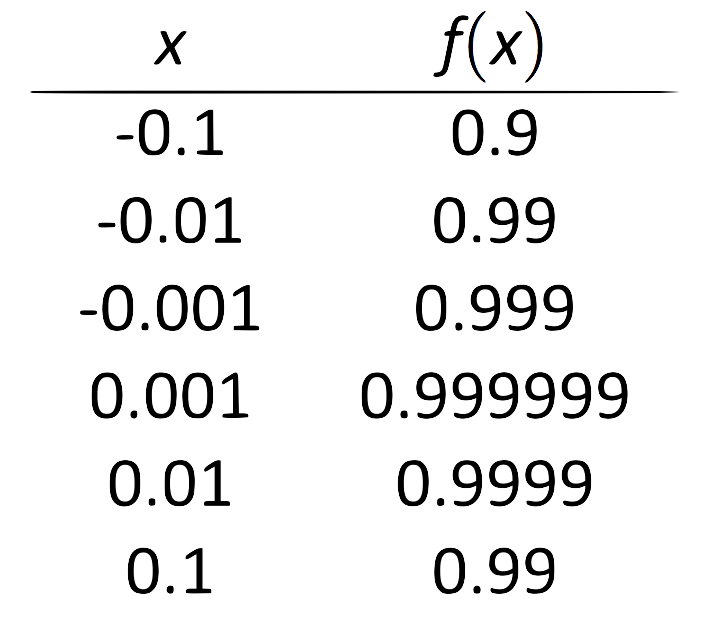
$\text{FIGURE 1.8}$: Чисельно наближаючи межу в прикладі 2.

Таблиця, показана на малюнку 1.8, показує значення$f(x)$ для значень$x$ близько 0. Зрозуміло, що оскільки$x$ приймає значення дуже близько 0,$f(x)$ приймає значення дуже близько 1. Виявляється, якщо ми дозволимо$x=0$ для будь-якого «шматочка»$f(x)$, 1 повертається; це важливо, і ми повернемося до цієї ідеї пізніше.

Графік і таблиця дозволяють нам сказати, що$\lim_{x\to 0}f(x) \approx 1$; насправді, ми, ймовірно, дуже впевнені, що це дорівнює 1.

Визначення, коли обмежень не існує

Функція може не мати обмеження для всіх значень$x$. Тобто ми не можемо сказати$\lim_{x\to c}f(x)=L$ для деяких чисел$L$ для всіх значень$c$, бо не може бути числа, яке$f(x)$ наближається. Існує три способи, за допомогою яких межа може не існувати.

Функція$f(x)$ може наближатися до різних значень по обидва боки$c$.
Функція може рости без верхньої або нижньої межі в міру$x$ підходів$c$.
Функція може коливатися в міру$x$ наближення$c$.

Ми вивчимо кожен з них по черзі.

Приклад 3: Різні значення наближаються зліва та справа

Дослідіть, чому$\lim_{x\to 1} f(x)$ не існує, де

\[f(x) = \left\{\begin{array}{cl} x^2-2x+3 & x\leq 1 \\ x & x>1 \end{array}\right. \]

$альт$
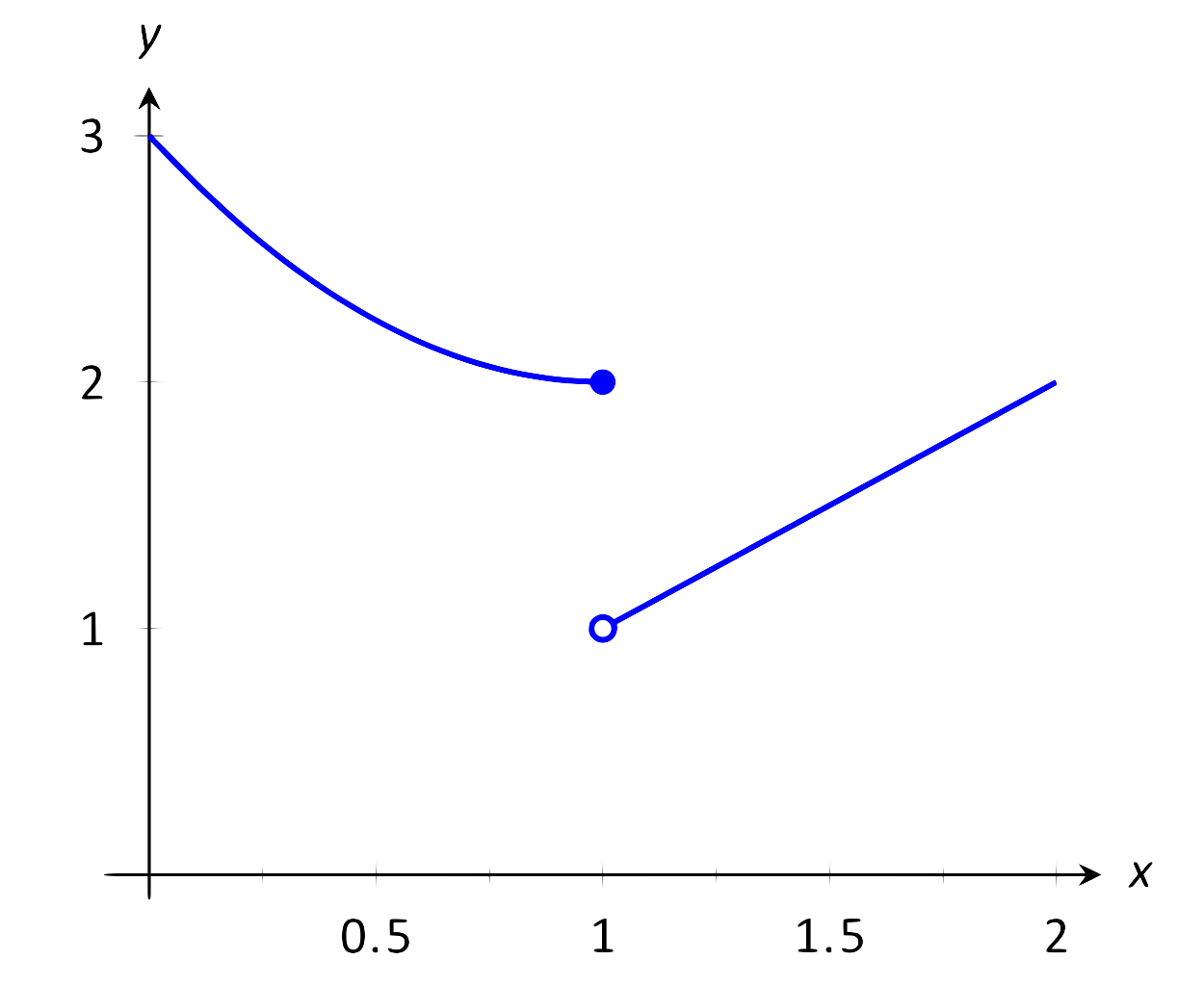
$\text{FIGURE 1.9}$: Не дотримуючись обмежень, як$x \to 1$ у прикладі 3.

$альт$
$\text{FIGURE 1.10}$: Значення$f(x)$ поблизу$x=1$ у прикладі 3.

Рішення:
Графік$f(x)$ навколо$x=1$ та таблицю наведено рисунки 1.9 та 1.10 відповідно. Зрозуміло, що в міру$x$ наближення до 1, здається,$f(x)$ не наближається до єдиного числа. Натомість здається, що$f(x)$ наближається до двох різних чисел. При розгляді значень$x$ менше 1 (наближаючись до 1 зліва), здається, що$f(x)$ наближається до 2; при розгляді значень$x$ більше 1 (наближаючись до 1 праворуч), здається, що$f(x)$ наближається до 1. Визнання такої поведінки важливо; пізніше ми вивчимо це більш глибоко. Зараз достатньо сказати, що межі не існує, оскільки не$f(x)$ наближається до одного значення, як наближається$x$ до 1.

Приклад 4: Функція росте без прив'язки

Дослідіть, чому$\lim_{x\to 1} 1/(x-1)^2$ не існує.

Рішення:
Графік і таблиця$f(x) = 1/(x-1)^2$ наведені на рисунках 1.11 і 1.12 відповідно. Обидва показують, що з$x$ наближенням до 1,$f(x)$ зростає все більше і більше.

$альт$
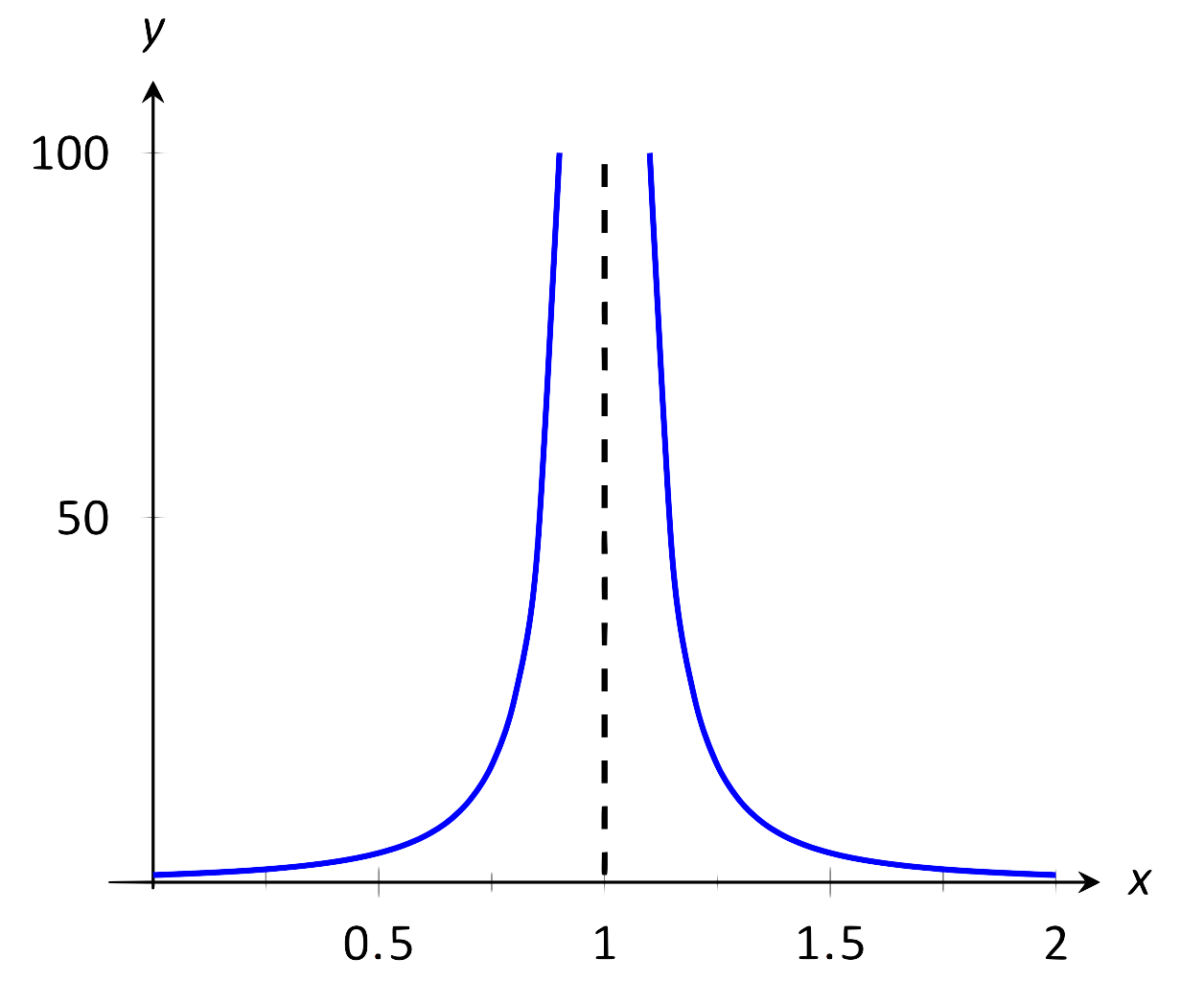
$\text{FIGURE 1.11}$: Не дотримуючись обмежень, як$x\to 1$ у прикладі 4.

$альт$
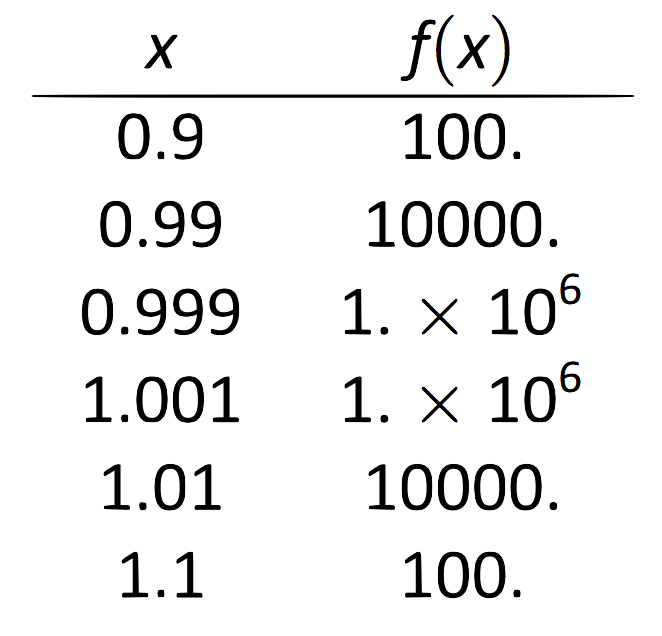
$\text{FIGURE 1.12}$: Значення$f(x)$ поблизу$x=1$ у прикладі 4.

Ми можемо вивести це самостійно, без допомоги графіка та таблиці. Якщо$x$ близько 1, то$(x-1)^2$ дуже мало, і:

\[\frac{1}{\text{very small number}} = \text{very large number}.\]

Оскільки$f(x)$ не наближається до єдиного числа, робимо висновок, що

\[\lim_{x\to 1}\frac{1}{(x-1)^2}\]

не існує.

Приклад 5: Функція коливається

Дослідіть, чому$\lim_{x\to 0}\sin(1/x)$ не існує.

Рішення:
Два графіки$f(x) = \sin(1/x)$ наведені на малюнках 1.13. Малюнок 1.13 (а) показує$f(x)$ на інтервалі$[-1,1]$; зверніть увагу$f(x)$, як здається, коливається поблизу$x=0$. Можна подумати, що незважаючи на коливання, як$x$ наближається до 0,$f(x)$ наближається до 0. Однак малюнок 1.13 (b) збільшується на$\sin(1/x)$ інтервалі$[-0.1,0.1]$. Тут коливання ще більш виражені. Нарешті, в таблиці на малюнку 1.13 (c) ми бачимо$\sin(x)/x$ оцінені для значень$x$ близько 0. Як$x$ наближається до 0,$f(x)$ здається, не наближається до будь-якого значення.

$альт$
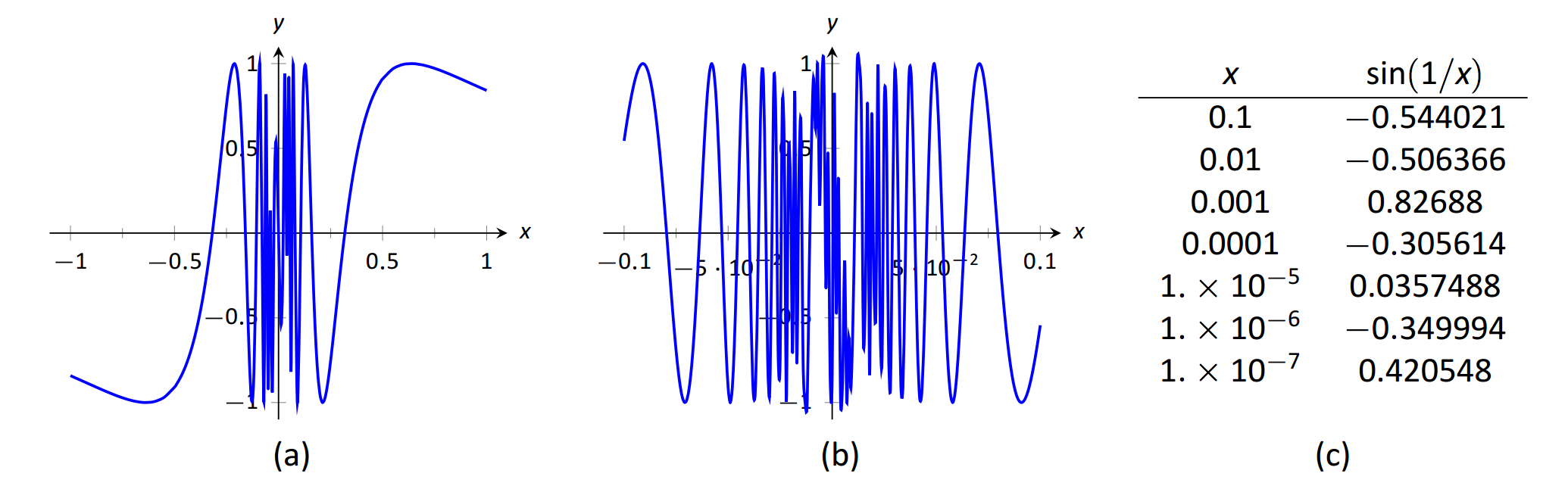
$\text{FIGURE 1.13}$: Спостерігаючи, що не$f(x)=\sin (1/x)$ має обмежень, як$x\to 0$ у прикладі 5.

Можна показати, що насправді,$x$ наближаючись до 0,$\sin(1/x)$ приймає всі значення від$-1$ 1 до нескінченного часу! Через це коливання,

$\lim_{x\to 0}\sin(1/x)$не існує.

Межі різницевих коефіцієнтів

Ми наблизили межі функцій,$x$ наближаючись до певного числа. Ще один важливий вид обмеження ми розглянемо після пояснення кількох ключових ідей.

$альт$
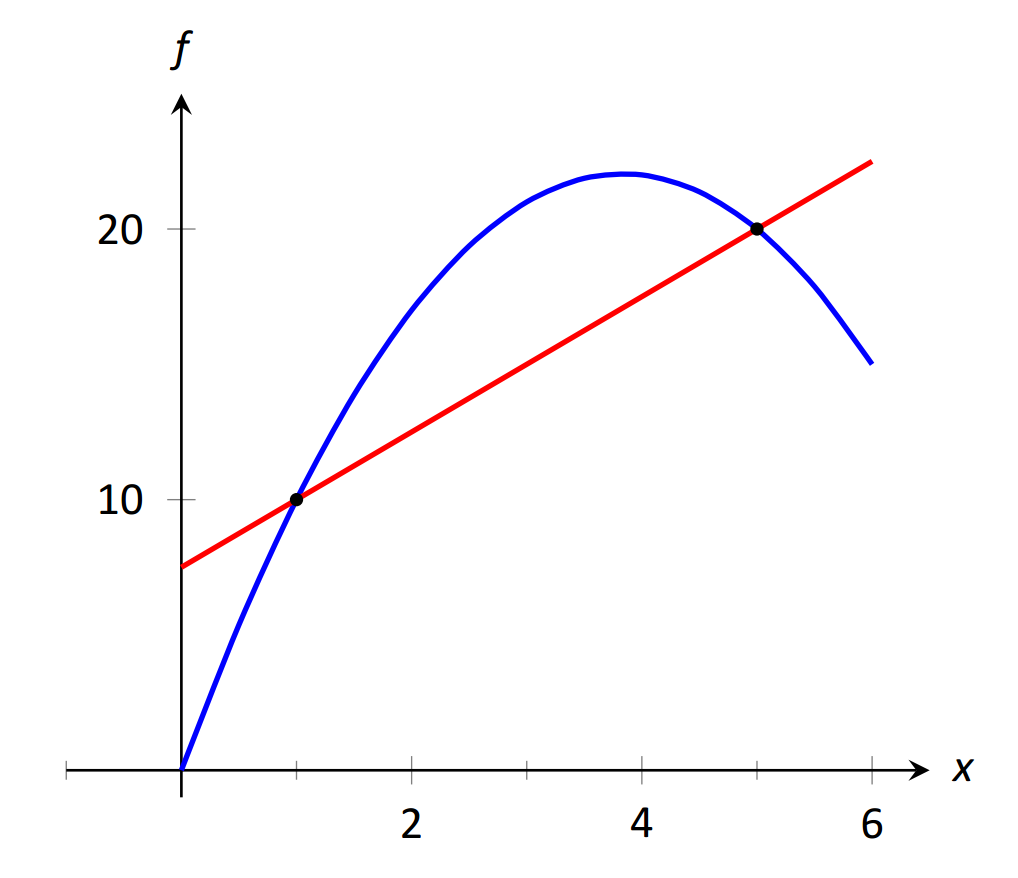
$\text{FIGURE 1.14}$: Інтерпретація різницевого коефіцієнта як нахилу січної лінії.

$f(x)$Дозволяти представляють функцію положення, в футах, деякі частинки, що рухається по прямій лінії, де$x$ вимірюється в секундах. Скажімо, коли$x=1$, частинка знаходиться в положенні 10 футів, а коли$x=5$, частка знаходиться на 20 футів. Інший спосіб висловити це - сказати:

\[f(1)=10 \quad \text{ and } \quad f(5) = 20.\]

Оскільки частка пройшла 10 футів за 4 секунди, ми можемо сказати, що середня швидкість частинки становила 2,5 футів/с Ми пишемо цей розрахунок, використовуючи «частку різниці», або, коефіцієнт різниці:

\[\frac{f(5) - f(1)}{5-1} = \frac{10}4 = 2.5 \text{ft/s}.\]

Цей коефіцієнт різниці можна розглядати як знайомий «підйом над бігом», який використовується для обчислення нахилів ліній. Насправді, це по суті те, що ми робимо: враховуючи дві точки на графіку$f$, ми знаходимо нахил січної лінії через ці дві точки. Див. Малюнок 1.14.

Тепер розглянемо знаходження середньої швидкості на іншому часовому проміжку. Ми знову починаємо з$x=1$, але розглянемо положення частинки через$h$ секунди. Тобто враховуйте положення частки коли$x=1$ і коли$x=1+h$. Коефіцієнт різниці зараз

\[\frac{f(1+h)-f(1)}{(1+h)-1} = \frac{f(1+h)-f(1)}h.\]

Нехай$f(x) = -1.5x^2+11.5x$; зауважте, що$f(1)=10$ і$f(5) = 20$, як в нашому обговоренні. Ми можемо обчислити цей коефіцієнт різниці для всіх значень$h$ (навіть негативних значень!) крім того$h=0$, тоді ми отримуємо «0/0», невизначену форму, введену раніше. Для всіх значень$h\neq 0$ різницевий коефіцієнт обчислює середню швидкість частинки протягом інтервалу часу довжини,$h$ починаючи з$x=1$.

Для малих значень$h$, тобто значень$h$ близьких до 0, ми отримуємо середні швидкості за дуже короткі проміжки часу і обчислюємо січні лінії на малих інтервалах. Див. Малюнок 1.15. Це змушує нас замислитися, що межа коефіцієнта різниці як$h$ наближається до 0. Тобто,

\[\lim_{h\to 0} \frac{f(1+h)-f(1)}{h} = \text{ ? }\]

$альт$ $альт$ $альт$
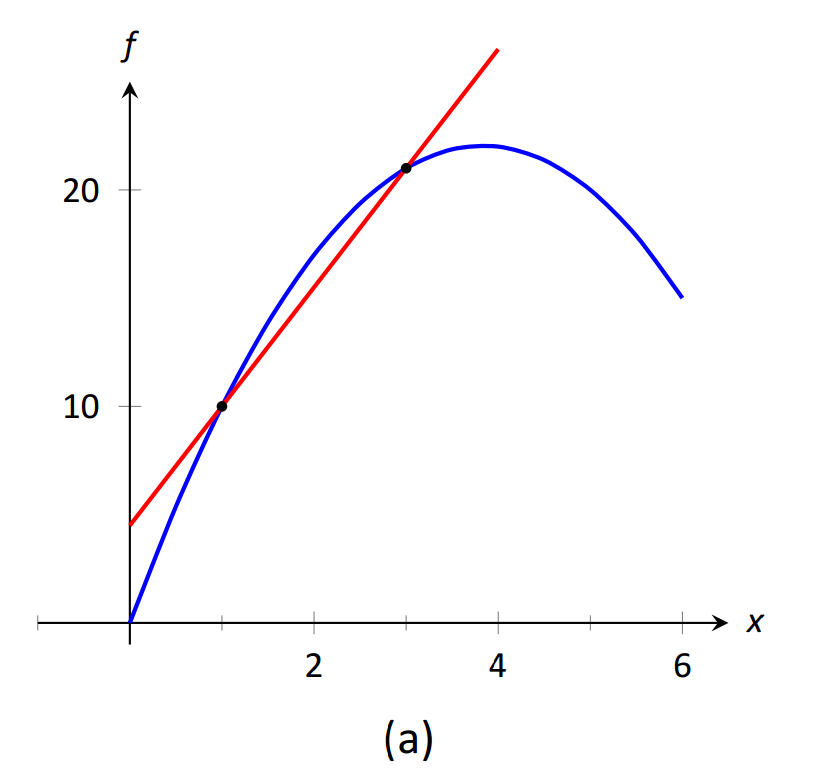
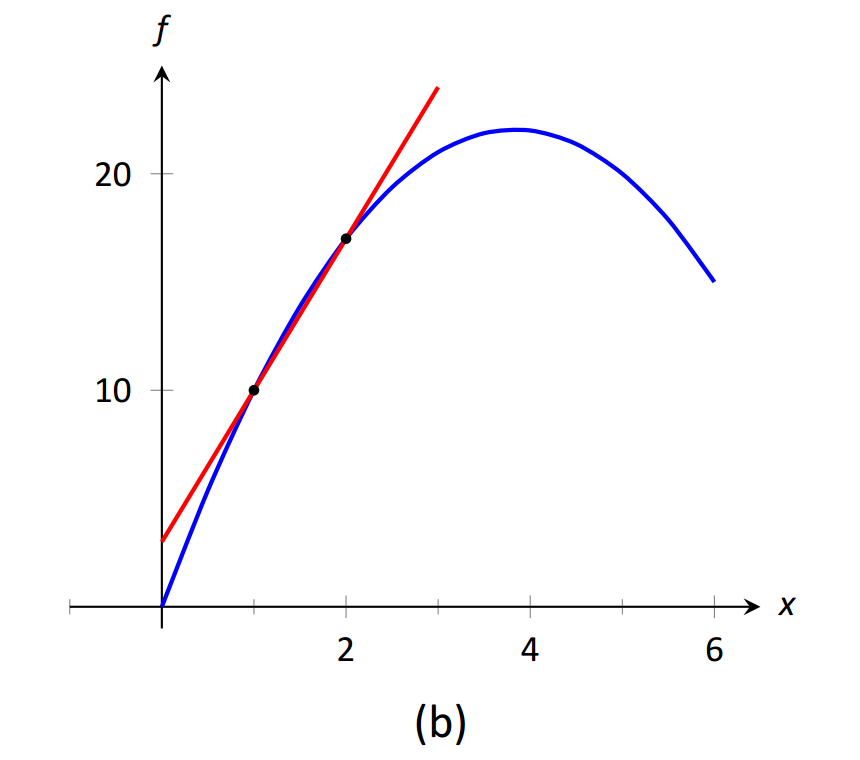
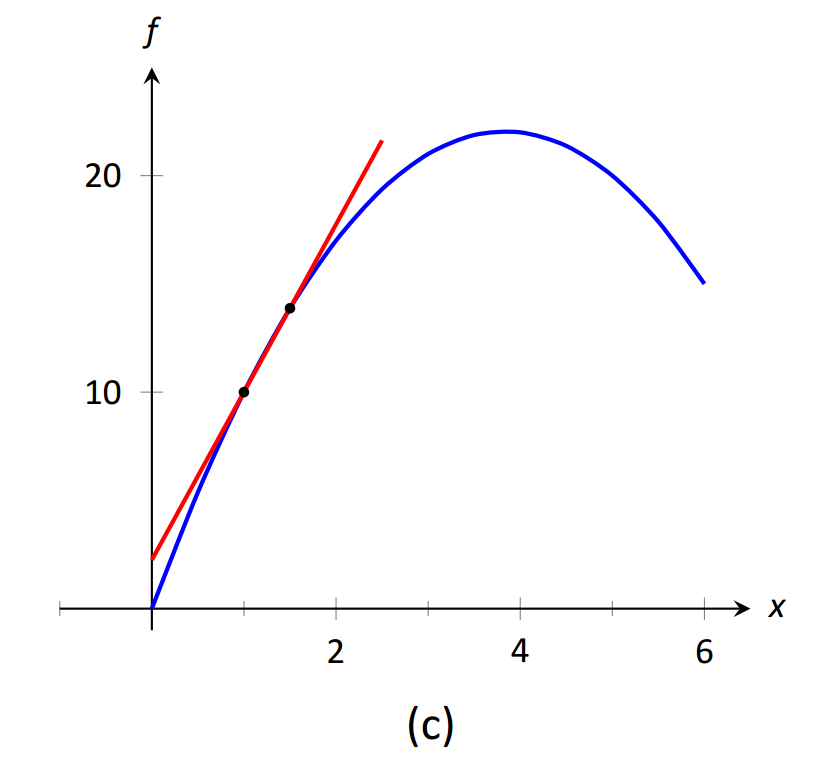
$\text{FIGURE 1.15}$: Січні рядки$f(x)$ at$x=1$ і$x=1+h$, для скорочуваних значень$h$ (тобто,$h\to 0$).

Оскільки ми ще не маємо істинного визначення межі або точного методу його обчислення, ми погоджуємося на наближення значення. Хоча ми могли б графікувати частку різниці (де$x$ -вісь буде представляти$h$ значення, а$y$ -вісь представлятиме значення різниці коефіцієнта), ми погоджуємося на створення таблиці. Див. Малюнок 1.16. Таблиця дає нам підстави припускати, що значення ліміту становить близько 8,5.

$альт$
$\text{FIGURE 1.16}$: Коефіцієнт різниці оцінюється при значеннях$h$ близько 0.

Правильне розуміння меж є ключем до розуміння числення. За допомогою обмежень ми можемо виконати, здавалося б, неможливі математичні речі, такі як складання нескінченної кількості чисел (а не отримати нескінченність) і знайти нахил лінії між двома точками, де «дві точки» насправді є однією і тією ж точкою. Це не просто математичні цікавості; вони дозволяють нам зв'язати положення, швидкість і прискорення разом, з'єднати площі поперечного перерізу з об'ємом, знайти роботу, виконану змінною силою, і багато іншого.

У наступному розділі ми дамо формальне визначення межі і починаємо наше дослідження знаходження меж аналітично. У наступних вправах продовжуємо наше введення і наближаємо значення лімітів.

Автори та атрибуція

Template:ContribApexCalc