1.3: Аналітичне знаходження меж

Last updated
Save as PDF

Page ID: 60791

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У розділі 1.1 ми досліджували поняття межі без суворого визначення, тобто ми могли робити лише наближення. У попередньому розділі ми дали визначення межі та продемонстрували, як його використовувати, щоб переконатися, що наші наближення були правильними. До сих пір наш метод знаходження межі дорівнює 1) зробити дійсно хороше наближення або графічно, або чисельно, і 2) переконайтеся, що наше наближення правильне за допомогою a$\epsilon$ -$\delta$ доказ.

Цей процес має свої недоліки, не останнім з яких є той факт, що$\epsilon$ —$\delta$ докази громіздкі. Цей розділ дає низку теорем, які дозволяють нам знаходити межі набагато швидше та інтуїтивно.

Визнаючи, що$\epsilon$ -$\delta$ докази громіздкі, цей розділ дає низку теорем, які дозволяють нам знаходити межі набагато швидше та інтуїтивно.

Припустимо$\lim\limits_{x\to 2} f(x)=2$, що$\lim\limits_{x\to 2} g(x) = 3$ і.Що таке$\lim\limits_{x\to 2}(f(x)+g(x))$? Інтуїція говорить нам, що межа повинна бути 5, оскільки ми очікуємо, що обмеження будуть вести себе приємно. Наступна теорема стверджує, що вже встановлені межі поводяться добре.

Теорема$\PageIndex{1}$: Basic Limit Properties

Дозволяти$b$$c$,$L$ і$K$ бути дійсними числами,$n$ Дозволяти бути додатним цілим числом,$f$ і нехай і$g$ бути функції з наступними обмеженнями:

\[\lim\limits_{x\to c}f(x) = L \text{ and } \lim\limits_{x\to c} g(x) = K.\nonumber\]

Наступні обмеження утримують.

Константи:$\displaystyle \lim\limits_{x\to c} b = b$
Ідентичність:$\displaystyle \lim\limits_{x\to c} x = c$
Суми/Відмінності:$\displaystyle \lim\limits_{x\to c}(f(x)\pm g(x)) = L\pm K$
Скалярні кратні:$\displaystyle \lim\limits_{x\to c} b\cdot f(x) = bL$
Продукція:$\displaystyle \lim\limits_{x\to c} f(x)\cdot g(x) = LK$
Коефіцієнти:$\displaystyle \lim\limits_{x\to c} f(x)/g(x) = L/K$, ($K\neq 0)$
Повноваження:$\displaystyle \lim\limits_{x\to c} f(x)^n = L^n$
Коріння:$\displaystyle \lim\limits_{x\to c} \sqrt[n]{f(x)} = \sqrt[n]{L}$
Композиції: Налаштуйте нашу раніше вказану граничну ситуацію на:

\[\lim\limits_{x\to c}f(x) = L,\ \lim\limits_{x\to L} g(x) = K \text{ and } g(L)=K .\]\[\text{Then } \lim\limits_{x\to c}g(f(x)) = K.\]

Робимо замітку про Property #8: коли$n$ парний,$L$ повинен бути більше 0. Якщо$n$ непарне, то твердження вірно для всіх$L$.

Застосовуємо теорему до прикладу.

Приклад$\PageIndex{1}$: Using Basic Limit Properties

Нехай

\[\lim\limits_{x\to 2} f(x)=2,\quad\lim\limits_{x\to 2} g(x) = 3\quad \text{ and }\quad p(x) = 3x^2-5x+7.\]

Знайдіть такі обмеження:

$ \lim\limits_{x\to 2} \big(f(x) + g(x)\big)$
$ \lim\limits_{x\to 2} \big(5f(x) + g(x)^2\big)$
$ \lim\limits_{x\to 2} p(x)$

Рішення

Використовуючи правило Сума/Різниця, ми це знаємо$ \lim\limits_{x\to 2} \big(f(x) + g(x)\big) = 2+3 =5$.
Використовуючи правила Scalar Multiple та Sum/Difference, ми виявляємо, що$ \lim\limits_{x\to 2} \big(5f(x) + g(x)^2\big) = 5\cdot 2 + 3^2 = 19.$
Тут ми об'єднуємо Power, Scalar Multiple, Сума/Різниця і Постійні Правила. Ми показуємо досить багато кроків, але загалом їх можна опустити:

\[\begin{align*} \lim\limits_{x\to 2} p(x) &= \lim\limits_{x\to 2} (3x^2-5x+7) \\ &= \lim\limits_{x\to 2} 3x^2-\lim\limits_{x\to 2} 5x+\lim\limits_{x\to 2}7 \\ &= 3\cdot 2^2 - 5\cdot 2+7 \\ &= 9 \end{align*}\]

Частина 3 попереднього прикладу демонструє, як межа квадратичного многочлена може бути визначена за допомогою властивостей Теореми 1. Мало того, визнати, що

\[\lim\limits_{x\to 2} p(x) = 9 = p(2);\]

тобто, межа на 2 була знайдена просто шляхом підключення 2 до функції. Це справедливо для всіх многочленів, а також для раціональних функцій (які є частками многочленів), як зазначено в наступній теоремі.

Теорема$\PageIndex{2}$ : Limits of Polynomial and Rational Functions

Межі поліноміальних і раціональних функцій} {Нехай$p(x)$ і$q(x)$ бути поліномами і$c$ дійсним числом. Потім:

$ \lim\limits_{x\to c} p(x) = p(c)$
$ \lim\limits_{x\to c} \frac{p(x)}{q(x)} = \frac{p(c)}{q(c)}$, де$q(c) \neq 0$.

Приклад$\PageIndex{2}$: Finding a limit of a rational function

Використовуючи теорему 2, знайдіть

\[\lim\limits_{x\to -1} \frac{3x^2-5x+1}{x^4-x^2+3}. \nonumber\]

Рішення

Використовуючи теорему$\PageIndex{2}$, ми можемо швидко констатувати, що

\[\begin{align*} \lim\limits_{x\to -1}\frac{3x^2-5x+1}{x^4-x^2+3} &= \frac{3(-1)^2-5(-1)+1}{(-1)^4-(-1)^2+3} \\ &= \frac{9}{3} =3. \end{align*}\]

Ймовірно, було неприємно в розділі 1.2 зробити багато роботи, щоб довести, що

\[\lim\limits_{x\to 2} x^2 = 4\]

як це здавалося досить очевидним. Попередні теореми стверджують, що багато функцій поводяться таким «очевидним» чином, що демонструє раціональна функція в прикладі 11.

Поліноміальні та раціональні функції - не єдині функції, які слід вести себе таким передбачуваним чином. Наступна теорема дає список функцій, поведінка яких особливо «приємна» з точки зору меж. У наступному розділі ми дамо формальну назву цим функціям, які ведуть себе «красиво».

Теорема$\PageIndex{4}$: Special Limits

$c$Дозволяти дійсне число в області даної функції і нехай$n$ бути натуральним числом. Наступні обмеження утримують:

\[\begin{align} &1.\lim\limits_{x\to c} \sin x = \sin c \quad &&4. \lim\limits_{x\to c} \csc x = \csc c\quad &&&7.\lim\limits_{x\to c} a^x = a^c (a>0) \\ &2. \lim\limits_{x\to c} \cos x = \cos c \quad &&5. \lim\limits_{x\to c} \sec x = \sec c \quad &&&8.\lim\limits_{x\to c} \ln x = \ln c \\ &3. \lim\limits_{x\to c} \tan x = \tan c \quad &&6.\lim\limits_{x\to c} \cot x = \cot c \quad &&&9. \lim\limits_{x\to c} \sqrt[n]{x} = \sqrt[n]{c} \end{align}\]

Приклад$\PageIndex{3}$: Evaluating limits analytically

Оцініть наступні межі.

$\lim\limits_{x\to \pi} \cos x$
$ \lim\limits_{x\to 3} (\sec^2x - \tan^2 x)$
$ \lim\limits_{x\to \pi/2} \cos x\sin x$
$ \lim\limits_{x\to 1} e^{\ln x}$
$ \lim\limits_{x\to 0} \frac{\sin x}{x}$

Рішення

Це просте застосування Теореми 3. $\lim\limits_{x\to \pi} \cos x = \cos \pi = -1$.
Ми можемо підійти до цього як мінімум двома способами. По-перше, безпосередньо застосовуючи теорему 3, ми маємо:\[\lim\limits_{x\to 3} (\sec^2x - \tan^2 x) = \sec^23-\tan^23.\] Використовуючи теорему Піфагора, цей останній вираз дорівнює 1; тому\[\lim\limits_{x\to 3} (\sec^2x - \tan^2 x) = 1.\] ми також можемо використовувати теорему Піфагора з самого початку. \[\lim\limits_{x\to 3} (\sec^2x - \tan^2 x) = \lim\limits_{x\to 3} 1 = 1,\]за допомогою правила Постійний ліміт. У будь-якому випадку, ми знаходимо межу 1.
Застосування граничного правила добутку теореми 1 та теореми 3 дає\[ \lim\limits_{x\to \pi/2} \cos x\sin x = \cos (\pi/2)\sin(\pi/2) = 0\cdot 1 = 0.\]
Знову ж таки, ми можемо підійти до цього двома способами. По-перше, ми можемо використовувати експоненціальну/логарифмічну ідентичність, яку$e^{\ln x} = x$ і оцінити$ \lim\limits_{x\to 1} e^{\ln x} = \lim\limits_{x\to 1} x = 1.$
Ми також можемо використовувати граничне правило композиції теореми 1. Використовуючи теорему 3, ми маємо$ \lim\limits_{x\to 1}\ln x = \ln 1 = 0$ і$\lim\limits_{x\to 0} e^x= e^0=1$, задовольняючи умовам правила композиції. Застосовуючи це правило, справедливі\[ \lim\limits_{x\to 1} e^{\ln x} = \lim\limits_{x\to 0} e^x = e^0 = 1.\] обидва підходи, що дають однаковий результат.
Ми зіткнулися з цим обмеженням у розділі 1.1. Застосовуючи наші теореми, ми намагаємося знайти межу, оскільки\[\lim\limits_{x\to 0}\frac{\sin x}{x}\rightarrow \frac{\sin 0}{0} \rightarrow \frac{"\,0\,"}{0}.\] Це, звичайно, порушує умову Теореми 1, оскільки межа знаменника не допускається бути 0. Тому ми все ще не можемо оцінити цю межу за допомогою інструментів, які ми маємо під рукою.

Розділ міг бути названий «Використання відомих обмежень для пошуку невідомих обмежень». Знаючи певні межі функцій, ми можемо знайти межі, що стосуються сум, продуктів, повноважень тощо цих функцій. Ми продовжуємо розробку таких порівняльних інструментів з теоремою Squeeze, розумним та інтуїтивним способом знайти значення деяких меж.

Перш ніж заявити цю теорему формально, припустимо$f$, що у нас є функції,$g$$f$ і$h$ де$g$ завжди приймає значення між і$h$; тобто для всіх$x$ в інтервалі,

\[f(x) \leq g(x) \leq h(x).\]

Якщо$f$ і$h$ мати однаковий ліміт при$c$, і завжди «$g$стискається» між ними, то$g$ повинен мати однаковий ліміт, а також. Це те, що говорить теорема про стискання.

Теорема$\PageIndex{5}$: Squeeze Theorem

Дозволяти$f$,$g$ і$h$ бути функції на відкритому інтервалі$I$ містять$c$ такі, що для всіх$x$ в$I$,

\[f(x)\leq g(x) \leq h(x).\]

Якщо

\[\lim\limits_{x\to c} f(x) = L = \lim\limits_{x\to c} h(x),\]

потім

\[\lim\limits_{x\to c} g(x) = L.\]

Може знадобитися певна робота, щоб з'ясувати відповідні функції, за допомогою яких можна «вичавити» задану функцію, з якої ви намагаєтеся оцінити ліміт. Однак, це, як правило, єдине місце роботи необхідно; теорема робить «оцінку граничної частини» дуже простою.

Ми використовуємо теорему Squeeze в наступному прикладі, щоб остаточно довести це$ \lim\limits_{x\to 0} \frac{\sin x}{x} = 1$.

Приклад$\PageIndex{4}$: Using the Squeeze Theorem

Скористайтеся теоремою стискання, щоб показати, що

\[ \lim\limits_{x\to 0} \frac{\sin x}{x} = 1. \nonumber\]

Рішення

Починаємо з розгляду одиничного кола. Кожна точка на одиничному колі має координати$(\cos \theta,\sin \theta)$ деякого кута$\theta$, як показано на малюнку$\PageIndex{1}$. Використовуючи подібні трикутники, ми можемо продовжити лінію від початку через точку до точки$(1,\tan \theta)$, як показано на малюнку. (Тут ми припускаємо, що$0\leq \theta \leq \pi/2$ .Пізніше ми покажемо, що ми також можемо розглянути$\theta \leq 0$.)

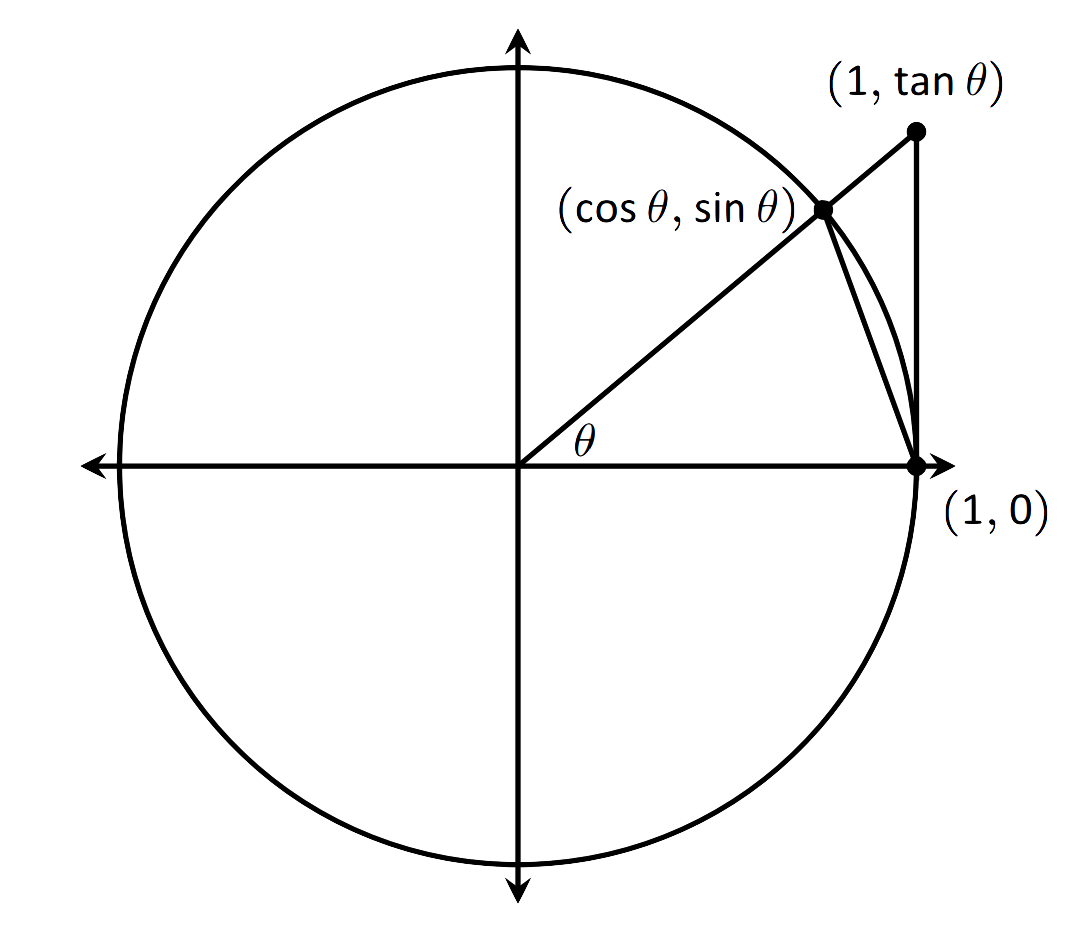
На малюнку 1.19 показано три області, побудовані в першому квадранті, два трикутники та сектор кола, які також намальовані нижче. Площа великого трикутника є$\frac12\tan\theta$; площа сектора є$\theta/2$; площа трикутника, що міститься всередині сектора, є$\frac12\sin\theta$. Тоді з діаграми зрозуміло, що

$альт$

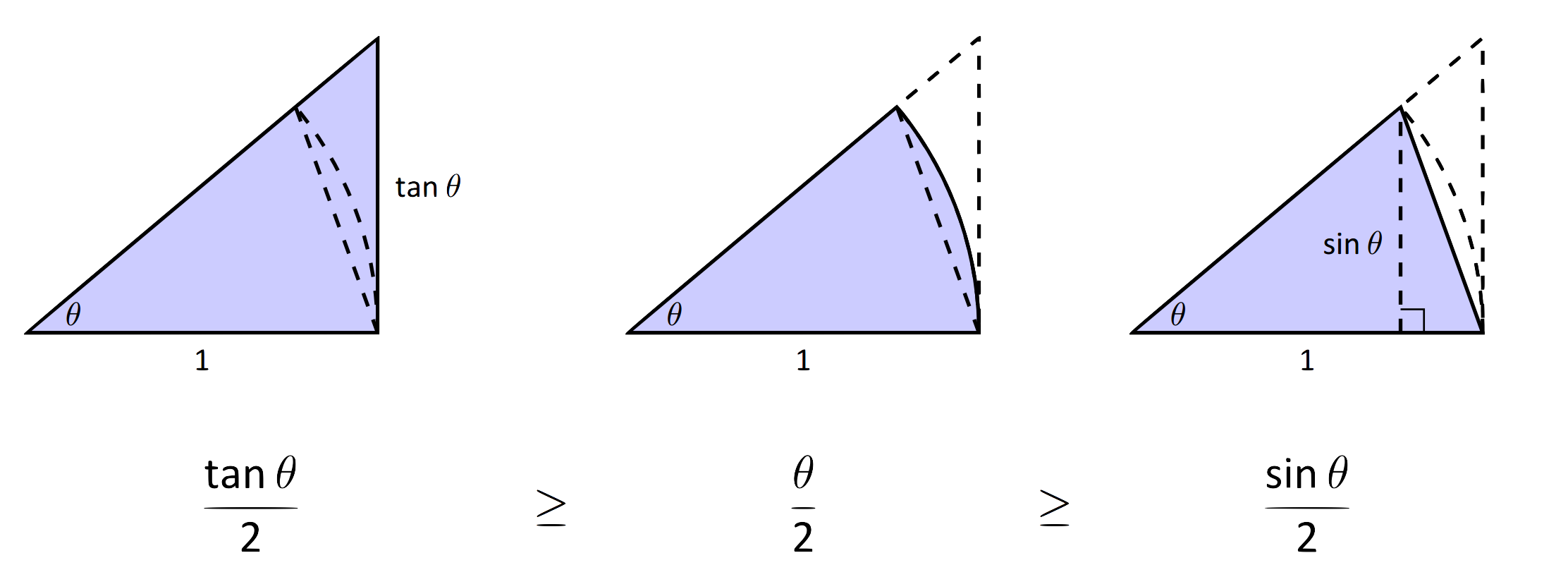
Помножте всі члени на$\frac{2}{\sin \theta}$, даючи

\[\frac{1}{\cos\theta} \geq \frac{\theta}{\sin \theta} \geq 1.\]

Прийняття взаємних обертає нерівності, даючи

\[ \cos \theta \leq \frac{\sin \theta}{\theta} \leq 1.\]

(Ці нерівності тримаються для всіх значень$\theta$ близько 0, навіть від'ємних значень, починаючи з$\cos (-\theta) = \cos \theta$ і$\sin (-\theta) = -\sin \theta$.)

Тепер візьміть обмеження.

\[\lim\limits_{\theta\to 0} \cos \theta \leq \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta} \leq \lim\limits_{\theta\to 0} 1 \]

\[\cos 0 \leq \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta} \leq 1 \]

\[1 \leq \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta} \leq 1 \]

Зрозуміло, це означає, що$ \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta}=1$

Варто згадати дві примітки про попередній приклад. По-перше, це додаток може не заохочувати, думаючи: «Я б ніколи не придумав це самостійно. Це занадто важко!» Не турбуйтеся; у цьому тексті ми проведемо вас у використанні Теореми про стискання. Коли людина отримує математичну зрілість, розумні докази, подібні до цього, легше і легше створювати.

По-друге, ця межа говорить нам більше, ніж просто те, що, коли$x$ наближається до 0,$\sin(x)/x$ наближається до 1. Обидва$x$ і$\sin x$ наближаються до 0, але співвідношення$x$ і наближається$\sin x$ до 1, що означає, що вони наближаються до 0 по суті однаково. Інший спосіб перегляду це: для$x$ малих функції$y=x$ і$y=\sin x$ по суті не відрізняються.

Ми включимо цю спеціальну межу разом з трьома іншими в наступну теорему.

Теорема$\PageIndex{5}$ : Special Limits

$ \lim\limits_{x\to 0} \frac{\sin x}{x} = 1$
$ \lim\limits_{x\to 0} \frac{\cos x-1}{x} = 0$
$ \lim\limits_{x\to 0} (1+x)^\frac1x = e$
$ \lim\limits_{x\to 0} \frac{e^x-1}{x} = 1$

Коротке слово про те, як інтерпретувати останні три межі. Ми знаємо, що як$x$ йде до 0,$\cos x$ йде до 1. Отже, у другій межі і чисельник, і знаменник наближаються до 0. Однак, оскільки межа дорівнює 0, ми можемо інтерпретувати це як те, що "$\cos x$наближається до 1 швидше, ніж$x$ наближається до 0».

У третій межі, всередині дужок ми маємо вираз, який наближається до 1 (хоча ніколи не дорівнює 1), і ми знаємо, що 1 піднятий до будь-якої потужності все ще 1. При цьому сила зростає до нескінченності. Що відбувається з числом біля 1, піднятим до дуже великої потужності? У цьому конкретному випадку результат наближається до числа Ейлера$e$, приблизно$2.718.$

У четвертій межі ми бачимо, що як$x\to 0$,$e^x$ наближається до 1 ``так само швидко»$x\to 0$, як, в результаті чого межа 1.

Наша остаточна теорема для цього розділу буде мотивована наступним прикладом.

Приклад$\PageIndex{5}$: Using algebra to evaluate a limit

Оцініть наступний ліміт:

\[\lim\limits_{x\to 1}\frac{x^2-1}{x-1}. \nonumber\]

Рішення

Ми починаємо з спроби застосувати теорему 3 і підставляючи 1 на$x$ частку. Це дає:

\[\lim\limits_{x\to 1}\frac{x^2-1}{x-1} = \frac{1^2-1}{1-1} = \frac{"\,0\,"}{0},\]

і невизначеною формою. Ми не можемо застосувати теорему.

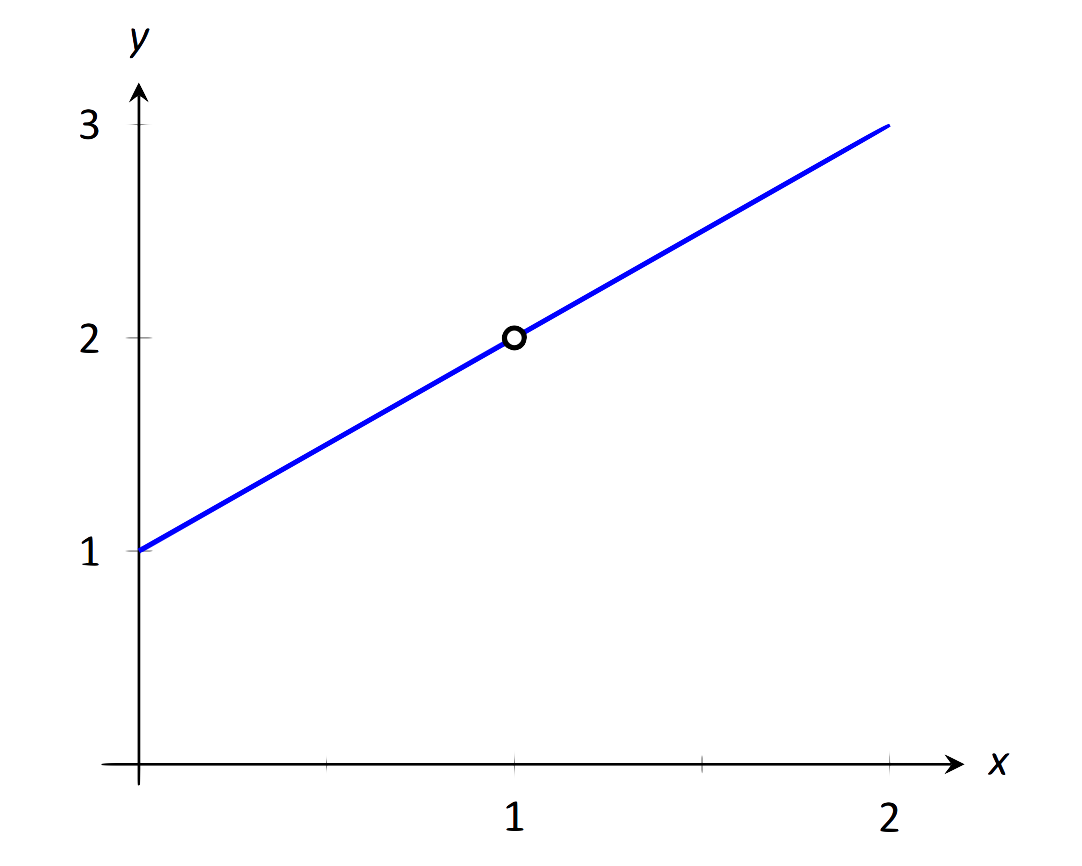
Графікуючи функцію, як на малюнку$\PageIndex{2}$, ми бачимо, що функція здається лінійною, маючи на увазі, що межа повинна бути легко оцінена. Визнайте, що чисельник нашого частки може бути врахований:

\[\frac{x^2-1}{x-1} = \frac{(x-1)(x+1)}{x-1}. \nonumber\]

Функція не визначена коли$x=1$, але для всіх інших$x$,

\[\require{cancel} \frac{x^2-1}{x-1} = \frac{(x-1)(x+1)}{x-1} = \frac{\cancel{(x-1)}(x+1)}{\cancel{x-1}}= x+1.\]

Чітко$ \lim\limits_{x\to 1}x+1 = 2$. Нагадаємо, що при розгляді меж нас не хвилює значення функції в 1, тільки значення, до якого функція наближається як$x$ до 1. Оскільки$(x^2-1)/(x-1)$ і$x+1$ однакові у всіх точках$x=1$, крім, вони обидва наближаються до того ж значення, що і$x$ підходи 1. Тому можна зробити висновок, що

\[\lim\limits_{x\to 1}\frac{x^2-1}{x-1}=2. \nonumber\]

Ключем до наведеного вище прикладу є те, що функції$y=(x^2-1)/(x-1)$ і$y=x+1$ ідентичні хіба що при$x=1$. Оскільки межі описують значення, до якого наближається функція, а не значення, яке насправді досягає функція, межі двох функцій завжди рівні.

Теорема$\PageIndex{6}$ : Limits of Functions Equal At All But One Point

Нехай$g(x) = f(x)$ для всіх$x$ у відкритому інтервалі, крім можливо в$c$, і нехай$ \lim\limits_{x\to c} g(x) = L$ для деякого реального числа$L$ .Тоді

\[\lim\limits_{x\to c}f(x) = L.\]

Фундаментальна теорема алгебри говорить нам, що при роботі з раціональною функцією виду$g(x)/f(x)$ і безпосередній оцінці межі$ \lim\limits_{x\to c} \frac{g(x)}{f(x)}$ повертає «0/0», то$(x-c)$ є множником обох$g(x)$ і$f(x)$. Потім можна використовувати алгебру для множення цього терміну, скасувати, а потім застосувати теорему 6. Ми це ще раз демонструємо.

Приклад$\PageIndex{6}$: Evaluating a limit using Theorem $\PageIndex{6}$

Оцінити

\[ \lim\limits_{x\to 3} \frac{x^3-2 x^2-5 x+6}{2 x^3+3 x^2-32 x+15}. \nonumber\]

Рішення

Почнемо з застосування теореми 3 і підставляючи 3$x$ для.Це повертає звичну невизначену форму «0/0".

Оскільки чисельник і знаменник є кожним многочленами, ми знаємо, що$(x-3)$ це коефіцієнт кожного. Використовуючи будь-який метод найбільш зручний для вас, враховуйте$(x-3)$ з кожного (за допомогою поліноміального поділу, синтетичного поділу, системи комп'ютерної алгебри і т.д.). Ми знаходимо, що

\[\frac{x^3-2 x^2-5 x+6}{2 x^3+3 x^2-32 x+15} = \frac{(x-3)(x^2+x-2)}{(x-3)(2 x^2+9 x-5)}. \nonumber\]

Ми можемо скасувати$(x-3)$ умови до тих пір, поки$x\neq 3$. Використовуючи теорему 6, робимо висновок:

\[\begin{align*}\lim\limits_{x\to 3} \frac{x^3-2 x^2-5 x+6}{2 x^3+3 x^2-32 x+15} &= \lim\limits_{x\to 3}\frac{(x-3)(x^2+x-2)}{(x-3)(2 x^2+9 x-5)} \\ &= \lim\limits_{x\to 3} \frac{(x^2+x-2)}{(2 x^2+9 x-5)}\\ &= \frac{10}{40} = \frac14. \end{align*}\]

Ми закінчуємо цей розділ переглядом ліміту, вперше поміченого в Розділі 1.1, обмеження коефіцієнта різниці. Нехай$f(x) = -1.5x^2+11.5x$; ми наблизили межу$ \lim\limits_{h\to 0}\frac{f(1+h)-f(1)}{h}\approx 8.5.$ Ми формально оцінюємо цю межу в наступному прикладі.

Приклад$\PageIndex{7}$ : Evaluating the limit of a difference quotient

Нехай$f(x) = -1.5x^2+11.5x$; знайти$ \lim\limits_{h\to 0}\frac{f(1+h)-f(1)}{h}.$

Рішення

Оскільки$f$ це поліном, наша перша спроба повинна полягати в тому, щоб використовувати теорему 3 і замінити 0 для$h$. Однак ми бачимо, що це дає нам «0/0». Знання того, що у нас є раціональна функція, натякає, що певна алгебра допоможе. Розглянемо наступні кроки:

\[\begin{align*} \lim\limits_{h\to 0}\frac{f(1+h)-f(1)}{h} &= \lim\limits_{h\to 0}\frac{-1.5(1+h)^2 + 11.5(1+h) - \left(-1.5(1)^2+11.5(1)\right)}{h} \\ &= \lim\limits_{h\to 0}\frac{-1.5(1+2h+h^2) + 11.5+11.5h - 10}{h}\\ &= \lim\limits_{h\to 0}\frac{-1.5h^2 +8.5h}{h}\\ &= \lim\limits_{h\to 0}\frac{h(-1.5h+8.5)}h\\ &= \lim\limits_{h\to 0}(-1.5h+8.5) \quad (\text{using Theorem 6, as $h\neq 0$}) \\ &= 8.5 \quad (\text{using Theorem 3}) \end{align*}\]

Це відповідає нашому попередньому наближенню.

Цей розділ містить кілька цінних інструментів для оцінки лімітів. Одним з основних результатів цього розділу є Теорема 3; він стверджує, що багато функцій, які ми використовуємо регулярно, поводяться дуже приємно, передбачувано. У наступному розділі ми даємо назву цій приємній поведінці; ми позначаємо такі функції як безперервні. Визначення цього терміну вимагатиме від нас знову поглянути на те, що таке межа і що призводить до того, що обмеження не існують.

Автори та атрибуція

Template:ContribApexCalc