Skip to main content
LibreTexts - Ukrayinska

1.3: Геометрія

  1. Last updated
  2. Save as PDF
  • Page ID
    66380

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Геометричні фігури, а також площа і обсяги часто можуть бути важливими при вирішенні проблем.

    Приклад\(\PageIndex{1}\)

    Вам цікаво, наскільки високе дерево, але не маєте ніякого способу піднятися на нього. Опишіть спосіб визначення висоти.

    Рішення

    Є кілька підходів, які ми могли б взяти. Ми будемо використовувати один на основі трикутників, який вимагає, щоб це був сонячний день. Припустимо, дерево кидає тінь, скажімо, довжиною 15 футів. Тоді я можу попросити друга допомогти мені виміряти власну тінь. Припустимо, я висотою 6 футів і кидаю тінь 1,5 футів. Оскільки трикутник, утворений деревом і його тінню, має ті ж кути, що і трикутник, утворений мною і моєю тінню, ці трикутники називаються подібними трикутниками, і їх сторони будуть масштабуватися пропорційно. Іншими словами, співвідношення висоти до ширини буде однаковим у обох трикутників. Використовуючи це, ми можемо знайти висоту дерева, яку позначимо\(h\):

    \[ \dfrac{6 \text{ ft tall}}{1.5 \text{ ft shadow}} = \dfrac{h \text{ ft tall}}{15 \text{ ft shadow}} \nonumber \]

    Помноживши обидві сторони на 15, отримуємо\(h\) = 60. Дерево має висоту близько 60 футів.

    Можливо, буде корисно згадати деякі формули для площ і обсягів декількох основних фігур.

    Визначення: Області

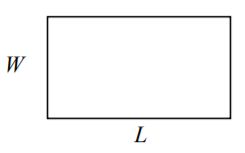
    Прямокутник

    Площа:\(L \cdot W\)

    Периметр:\(2L + 2W\)

    clipboard_e5d5868122c3c6e9a11cd5755b93a3618.png

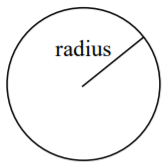
    Коло, радіус\(r\)

    Площа:\(\pi r^2\)

    Окружність:\( 2 \pi r \)

    clipboard_e4356d8ca9ba07adcbbd71b698a023bce.png

    Визначення: обсяги

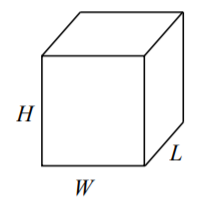
    Прямокутна коробка

    Обсяг:\(L \cdot W \cdot H\)

    clipboard_ed9c29b0190bf6b2391b9385514d7626a.png

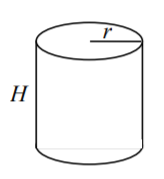
    Циліндр

    Обсяг:\(\pi r^2 H\)

    clipboard_ec38ffaaca837b6df5351ac5105c1032b.png

    Приклад\(\PageIndex{2}\)

    Якщо для піци діаметром 12 дюймів потрібно 10 унцій тіста, скільки тіста потрібно для 16-дюймової піци?

    Рішення

    Щоб відповісти на це питання, потрібно розглянути, як буде масштабуватися вага тесту. Вага буде грунтуватися на обсязі тесту. Однак, оскільки обидві піци будуть приблизно однакової товщини, вага буде масштабуватися з площею верхньої частини піци. Ми можемо знайти площу кожної піци, використовуючи формулу площі кола\(A = \pi r^2\):

    12-дюймова піца має радіус 6 дюймів, тому площа буде\(\pi \cdot 6^2 ≈ 113\) квадратними дюймами.

    16-дюймова піца має радіус 8 дюймів, тому площа буде\(\pi \cdot 8^2 ≈ 201\) квадратними дюймами.

    Зверніть увагу, що якби обидві піци були товщиною 1 дюйм, обсяги становили б 113 дюймів\(^3\) і 201\(^3\) відповідно, які знаходяться в тому ж співвідношенні, що і площі. Як вже говорилося раніше, оскільки товщина однакова для обох піц, можна сміливо її ігнорувати.

    Тепер ми можемо встановити пропорцію, щоб знайти вагу тіста для 16-дюймової піци:

    \[ \dfrac{10 \text{ ounces}}{113 \text{ in}^2} = \dfrac{x \text{ ounces}}{201 \text{ in}^2} \nonumber \]

    Помножте обидві сторони на 201:\( x = 201 \cdot \dfrac{10}{113} ≈ 17.8 \) унції тіста для 16-дюймової піци.

    Цікаво відзначити, що поки діаметр в\( \dfrac{16}{12} = 1.33\) рази більше, потрібне тісто, яке масштабується з площею, в\(1.33^2 = 1.78\) рази більше.

    Приклад\(\PageIndex{3}\)

    Компанія виготовляє звичайний і джамбо зефір. Звичайний зефір має 25 калорій. Скільки калорій матиме зефір джамбо?

    Рішення

    Ми очікуємо, що калорії масштабуватимуться з об'ємом. Оскільки зефір має циліндричну форму, ми можемо використовувати цю формулу, щоб знайти об'єм. З сітки на зображенні ми можемо оцінити радіус і висоту кожного зефіру.

    Звичайний зефір, здається, має діаметр близько 3,5 одиниць, даючи радіус 1,75 одиниці, і висоту близько 3,5 одиниць. Обсяг - близько\( \pi (1.75)^2 (3.5) = 33.7 \text{ units}^3 \).

    Звичайний зефір, здається, має діаметр близько 5,5 одиниць, даючи радіус 2,75 одиниці, а висоту близько 5 одиниць. Обсяг - близько\( \pi (2.75)^2 (5) = 118.8 \text{ units}^3 \).

    Тепер ми могли б встановити пропорцію, або використовувати ставки. Звичайний зефір має 25 калорій на 33,7 кубічних одиниць об'єму. Зефір джамбо матиме:

    \[ 118.8 \text{ units}^3 \cdot \dfrac{25 \text{ calories}}{33.7 \text{ units}^3 } = 88.1 \text{ calories} \nonumber \]

    Цікаво відзначити, що в той час як діаметр і висота приблизно в 1,5 рази більше для зефіру джамбо, обсяг і калорії приблизно в 1,53 = 3,375 рази більше.

    Спробуйте зараз 5

    На веб-сайті сказано, що вам знадобиться 48 п'ятдесятифунтових мішків піску, щоб заповнити пісочницю розміром 8 футів на 8 футів на 1 фут. Скільки мішків вам знадобиться для пісочниці 6 футів на 4 фути на 1 фут?