Skip to main content
LibreTexts - Ukrayinska

1.8: Периметр і окружність

  1. Last updated
  2. Save as PDF
  • Page ID
    65882

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ви можете використовувати калькулятор у цьому модулі, якщо це необхідно.

    Периметр

    Багатокутник - замкнута геометрична фігура з прямими сторонами. Загальні багатокутники включають трикутники, квадрати, прямокутники, паралелограми, трапеції, п'ятикутники, шестикутники, восьмикутники... Периметр багатокутника - це відстань навколо зовнішньої сторони. Загалом, щоб знайти периметр багатокутника, можна скласти довжини всіх його сторін.

    Крім того, якщо ви ще цього не зробили, зараз саме час звикнути включати одиниці у свої відповіді.

    Вправи\(\PageIndex{1}\)

    1. Знайдіть периметр трикутника.

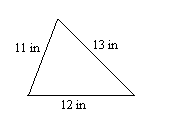
    трикутник зі сторонами, позначені 11 в, 13 в, 12 в

    2. Знайдіть периметр трапеції.

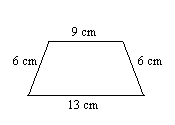
    трапеція з маркуванням сторін 6 см, 9 см, 6 см, 13 см

    Відповідь

    1. \(36\)в

    2. \(34\)см

    Якщо ми знаємо, що деякі сторони багатокутника рівні, ми можемо використовувати формулу як альтернативу для складання всіх довжин окремо. Перша формула, наведена нижче, використовує змінну\(s\) для сторони квадрата. Формули прямокутника використовують\(l\) для довжини та\(w\) ширини, або\(b\) для основи та\(h\) висоти; ці терміни є взаємозамінними.

    Формули периметра

    Квадрат:\(P=4s\)

    Прямокутник:\(P=2l+2w\) або\(P=2b+2h\)

    Прямокутник:\(P=2(l+w)\) або\(P=2(b+h)\)

    Вправи\(\PageIndex{1}\)

    3. Знайдіть периметр квадрата.

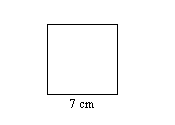
    квадрат з нижньою стороною маркуванням 7 см

    4. Знайдіть периметр прямокутника.

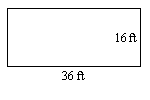
    прямокутник з правою стороною позначені 16 футів і нижня сторона маркована 36 футів

    5. Зона зберігання, яка являє собою прямокутник довжиною\(45\) футів і шириною\(20\) футів, повинна бути огороджена навколо всіх чотирьох сторін. Скільки футів огорожі потрібно? (Щоб зробити це простим, ігноруйте будь-які ворота або інші ускладнення.)

    6. Джанкарло ставить ліплення корони навколо краю стелі своєї вітальні. Якщо кімната являє собою прямокутник\(12\) -фут на\(16\) фут, скільки ліплення корони йому потрібно?

    Відповідь

    3. \(28\)см

    4. \(104\)футів

    5. \(130\)футів

    6. \(56\)футів

    Сторони правильного багатокутника всі рівні по довжині. Тому множення довжини сторони на кількість сторін дасть нам периметр.

    Формула периметра

    Правильний багатокутник зі\(n\) сторонами довжини\(s\):

    \[P=n\cdot{s} \nonumber \]

    Вправи\(\PageIndex{1}\)

    Знайдіть периметр кожного правильного багатокутника.

    7. Кожна сторона шестикутника має довжину\(4\) дюймів.

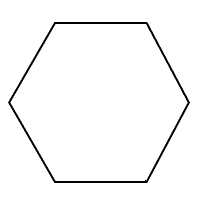
    правильний шестикутник (6 сторін)

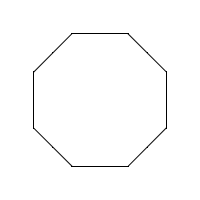
    8. Кожна сторона восьмикутника\(2.5\) завдовжки сантиметрів.

    звичайний восьмикутник (8 сторін)

    Відповідь

    7. \(24\)в

    8. \(20\)см

    Окружність

    Замість того, щоб називати його периметром, відстань по зовнішній стороні кола називається окружністю. Давайте розглянемо деяку лексику кола, перш ніж рухатися далі.

    Кожна точка на колі знаходиться на однаковій відстані від його центру. Ця відстань від центру до краю кола називається радіусом. Відстань від одного краю до іншого, через центр кола, називається діаметром. Як бачите, діаметр в два рази перевищує довжину радіуса.

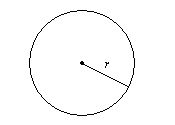
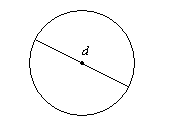
    коло з лінією від центру до краю, позначений rколо з лінією від краю до краю, що проходить через центр, позначений d

    Протягом історії різні цивілізації виявили, що окружність кола трохи більше, ніж в\(3\) рази перевищує довжину його діаметра. До 2000 року до н.е. Вавилоняни використовували значення,\(3\dfrac{1}{8}=3.125\) а єгиптяни використовували значення\(3\dfrac{13}{81}\approx3.1605\). [1] Значення\(3\dfrac{1}{7}\approx3.1429\) є ще кращим наближенням для відношення окружності до діаметра. Однак фактичне значення не може бути записано як точний дріб. Це ірраціональне число\(\pi\), вимовляється «пиріг», яке приблизно\(3.14159\).

    Формули окружності

    \[C=\pi{d} \nonumber \]

    \[C=2\pi{r} \nonumber \]

    Будь-який науковий калькулятор матиме\(\pi\) ключ; використання цього дасть вам найбільш точний результат, хоча ви повинні бути впевнені, щоб округлити відповідь належним чином. (Див. цей модуль, якщо вам потрібна освіга щодо округлення з множенням або діленням.) Багато людей використовують\(3.14\) як наближення для\(\pi\), але це може призвести до помилки округлення; якщо ви повинні використовувати наближення,\(3.1416\) краще, ніж\(3.14\).

    Іноді ми згинаємо правила в цьому підручнику і просимо округлити до певного місця значення замість округлення до певної кількості значущих цифр.

    Вправи\(\PageIndex{1}\)

    Обчисліть окружність кожного кола. Округлити до найближчої десятої.

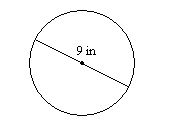
    9. коло діаметром з маркуванням 9 дюймів

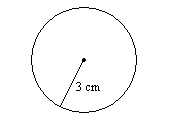
    10. коло з маркуванням радіусом 3 см

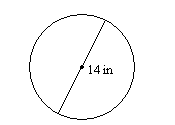
    11. коло діаметром з маркуванням 14 дюймів

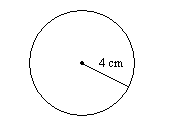
    12. коло з маркуванням радіусом 4 см

    Відповідь

    9. \(28.3\)в

    10. \(18.8\)см

    11. \(44.0\)в

    12. \(25.1\)см

    1. Ця інформація походить з глави 1 книги «Історія Пі» Петра Бекмана. Це напрочуд цікаве читання. ←