2.5: Рівнобедрені трикутники

У розділі 1.6 ми визначили трикутник рівнобедреним, якщо дві його сторони рівні. $\PageIndex{1}$На малюнку зображений рівнобедрений трикутник$\triangle ABC$ с$AC=BC$. У$\triangle ABC$ ми говоримо, що$\angle A$ є протилежною стороною$BC$ і$\angle B$ є протилежною стороною$AC$.

$\triangle ABC$Малюнок$\PageIndex{1}$: рівнобедрений з AC = BC.

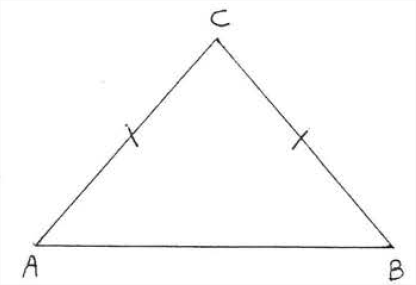
Найважливішим фактом про рівнобедрених трикутників є наступне:

Теорема$\PageIndex{1}$

Якщо дві сторони трикутника рівні, кути протилежні ці сторони рівні.

Теорема$\PageIndex{1}$ означає, що якщо$AC = BC$ в$\triangle ABC$ то$\angle A = \angle B$.

Приклад$\PageIndex{1}$

Знайти$x$:

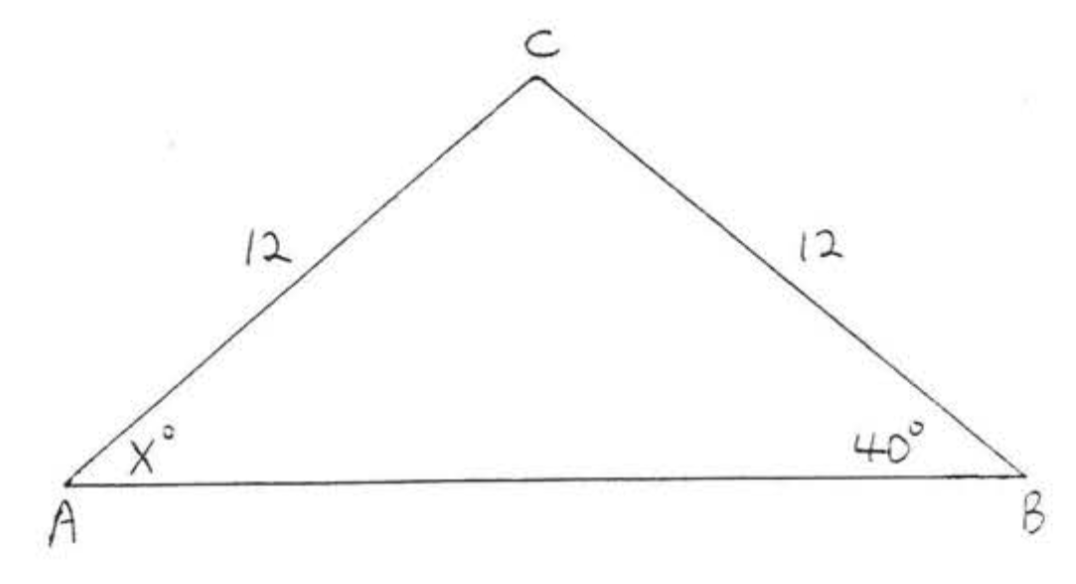
Рішення

$AC = BC$так$\angle A = \angle B$. Тому,$x = 40$.

Відповідь:$x = 40$.

У$\triangle ABC$ якщо$AC = BC$ то сторона$AB$ називається основою трикутника і$\angle A$ і$\angle B$ називається базовими кутами. Тому теорема$\PageIndex{1}$ іноді викладається наступним чином: «Базові кути рівнобедреного трикутника рівні»

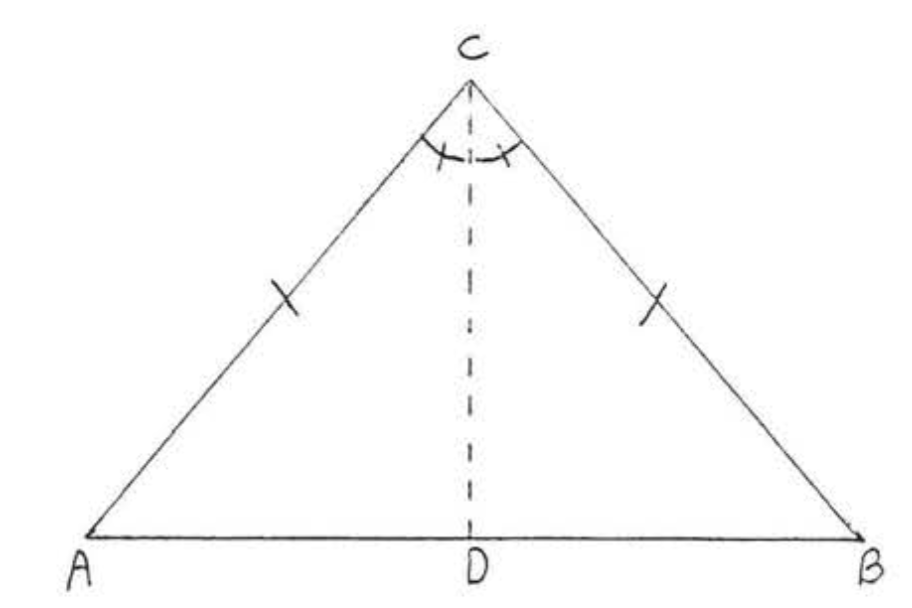
Доказ теореми$\PageIndex{1}$: Намалюйте$CD$, кут бісектриси$\angle ACB$ (рис.$\PageIndex{2}$). Решта доказів буде представлена у вигляді подвійних стовпців. Ми дали, що$AC = BC$ і$\angle ACD = \angle BCD$. Треба довести$\angle A = \angle B$.

Малюнок$\PageIndex{2}$: Малюємо$CD$, кут бісектриси$\angle ACB$.

Заяви	причини
1. $AC = BC$.	1. Враховуючи,$\triangle ABC$ є рівнобедреним.
2. $\angle ACD = \angle BCD$.	2. Задано,$CD$ є кутом бісектриси$\angle ACB$.
3. $CD = CD$.	3. Ідентичність.
4. $\triangle ACD \cong \triangle BCD$.	4. $SAS = SAS$:$AC, \angle C, CD$ з$\triangle ACD = BC$,$\angle C, CD$ з$\triangle BCD$.
5. $\angle A = \angle B$.	5. Відповідні кути конгруентних трикутників рівні.

Приклад$\PageIndex{2}$

Знайти$x, \angle A, \angle B$ і$\angle C$:

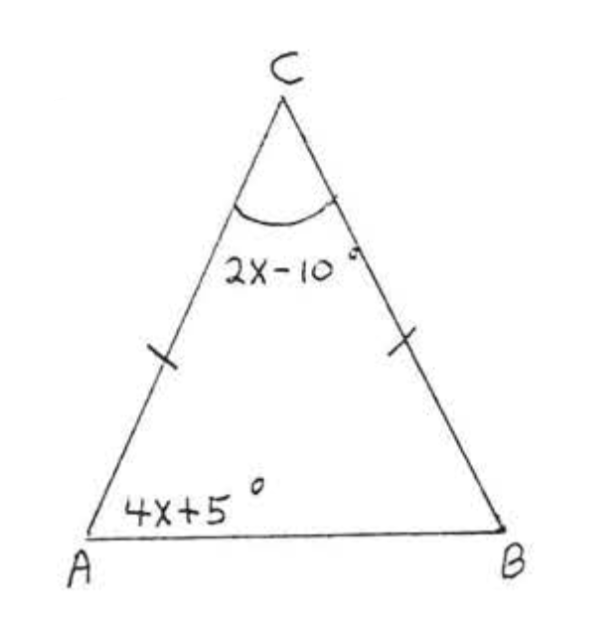
Рішення

$\angle B = \angle A = 4x + 5^{\circ}$за теоремою$\PageIndex{1}$. We have

$$\begin{array} {rcl} {\angle A + \angle B + \angle C} & = & {180^{\circ}} \\ {4x + 5 + 4x + 5 + 2x - 10} & = & {180} \\ {10x} & = & {180} \\ {x} & = & {18} \end{array}$$

$\angle A = \angle B = 4x + 5^{\circ} = 4(18) + 5^{\circ} = 72 + 5^{\circ} = 77^{\circ}$.

$\angle C = 2x - 10^{\circ} = 2(18) - 10^{\circ} = 36 - 10^{\circ} = 26^{\circ}$.

Перевірити

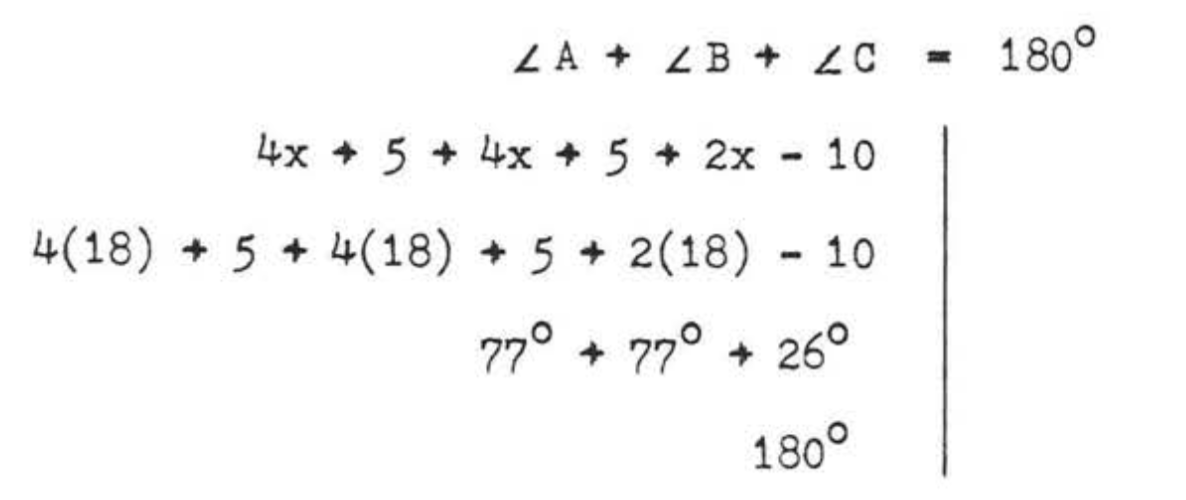
Відповідь

$x = 18$,$\angle A = 77^{\circ}$,$\angle B = 77^{\circ}$,$\angle C = 26^{\circ}$.

У теоремі$\PageIndex{1}$ ми припустили$AC = BC$ і довели$\angle A = \angle B$. Тепер ми припустимо$\angle A = \angle B$ і доведемо$AC = BC$. '1ihen припущення та висновок твердження поміняються, результат називається зворотним вихідним твердженням.

Теорема$\PageIndex{2}$: The Converse of Theorem $\PageIndex{1}$)

Якщо два кути трикутника рівні, сторони протилежні ці кути рівні.

Якщо малюнок 4, якщо$\angle A = \angle B$ тоді$AC = BC$.

Малюнок$\PageIndex{4}$. $\angle A = \angle B$

Приклад$\PageIndex{3}$

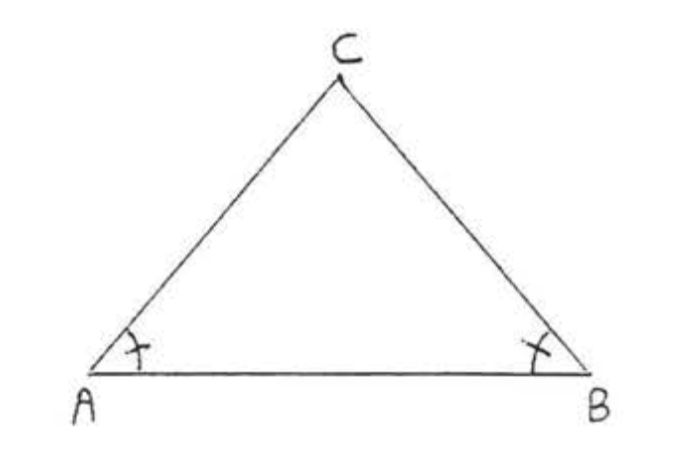
Знайти$x$

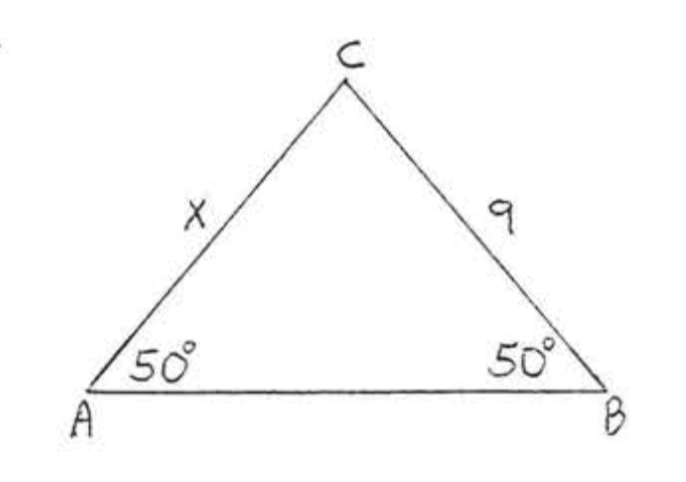
Рішення

$\angle A = \angle B$так$x = AC = BC = 9$ за теоремою$\PageIndex{2}$.

Відповідь

$x = 9$.

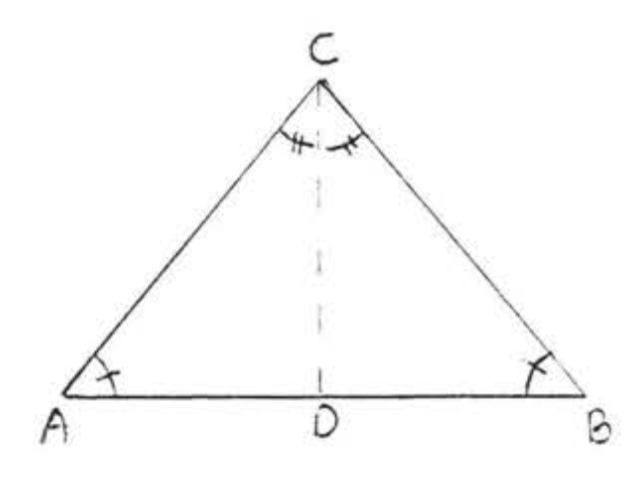
Доказ теореми$\PageIndex{2}$: Draw $CD$ the angle bisector of $\angle ACB$ (Figure $\PageIndex{5}$). We have $\angle ACD = \angle BCD$ and $\angle A = \angle B$. We must prove $AC = BC$.

Малюнок$\PageIndex{5}$. Draw $CD$, the angle bisector of $\angle ACB$.

Заяви	причини
1. $\angle A = \angle B$.	1. Дано.
2. $\angle ACD = \angle BCD$.	2. Дано.
3. $CD = CD$.	3. Ідентичність.
4. $\triangle ACD \cong \triangle BCD$.	4. $AAS = AAS$:$\angle A, \angle C, CD$$\triangle ACD = \angle B$ оф$\angle C$,$CD$ оф$triangle BCD$.
5. $AC = BC$.	5. Відповідні сторони конгруентних трикутників рівні

Наступні дві теореми є наслідками (безпосередніми наслідками) двох попередніх теорем:

Теорема$\PageIndex{3}$

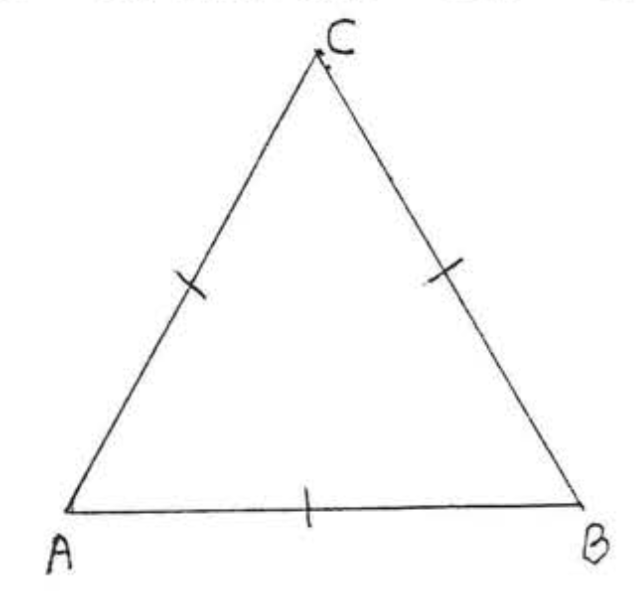
Рівносторонній трикутник рівнокутний.

На малюнку$\PageIndex{7}$, if $AB = AC = BC$ then $\angle A = \angle B = \angle C$.

Малюнок$\PageIndex{7}$:$\angle ABC$ рівносторонній.

Доказ

$AC = BC$так за теоремою$\PageIndex{1}$ $\angle B = \angle C$. Therefore $\angle A = \angle B = \angle C$.

Так як сума кута дорівнює$180^{\circ}$ we must have in fact that $\angle A = \angle B = \angle C = 60^{\circ}$.

Теорема$\PageIndex{4}$: The Converse of Theorem $\PageIndex{3}$)

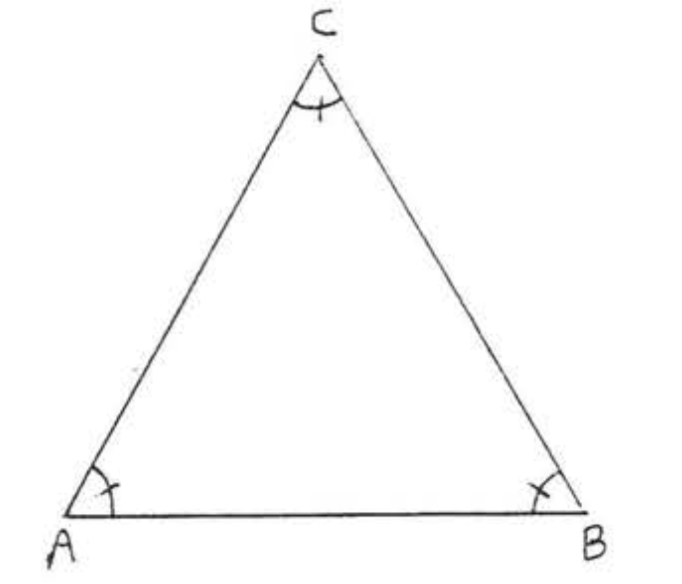
Рівнокутний трикутник рівносторонній.

На малюнку$\PageIndex{8}$, if $\angle A = \angle B = \angle C$ then $AB = AC = BC$.

Малюнок$\PageIndex{8}$. $\angle ABC$ is equiangular.

Доказ

$\angle A = \angle B$так за теоремою$\PageIndex{2}$, $AC = BC$, $\angle B = \angle C$ by Theorem $\PageIndex{2}$, $AB = AC$. Therefore $AB = AC = BC$.

Приклад$\PageIndex{4}$

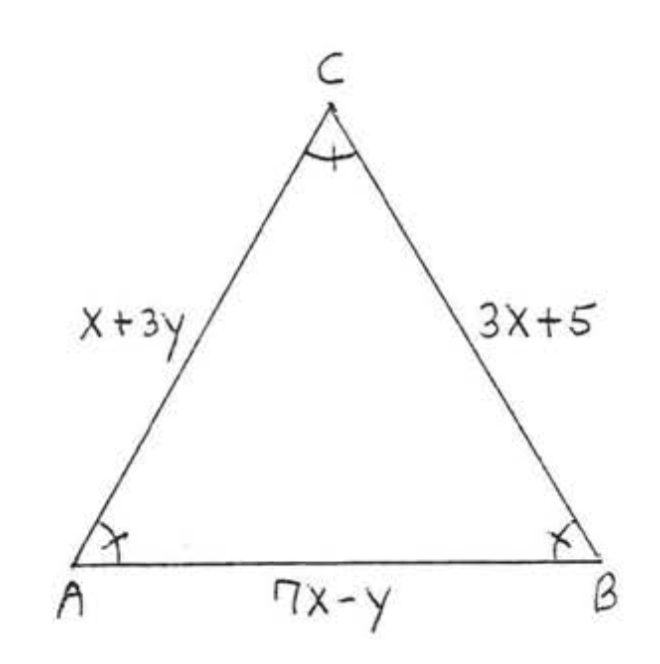
Знайти$x$,$y$ і$AC$:

Рішення

$\triangle ABC$є рівнокутним і так по теоремі$\PageIndex{4}$ is equilateral.

Тому$\begin{array} {rcl} {AC} & = & {AB} \\ {x + 3y} & = & {7x - y} \\ {x - 7x + 3y + y} & = & {0} \\ {-6x + 4y} & = & {0} \end{array}$ and $\begin{array} {rcl} {AB} & = & {BC} \\ {7x - y} & = & {3x + 5} \\ {7x - 3xy - y} & = & {5} \\ {4x - y} & = & {5} \end{array}$

У нас є система з двох рівнянь у двох невідомих для вирішення:

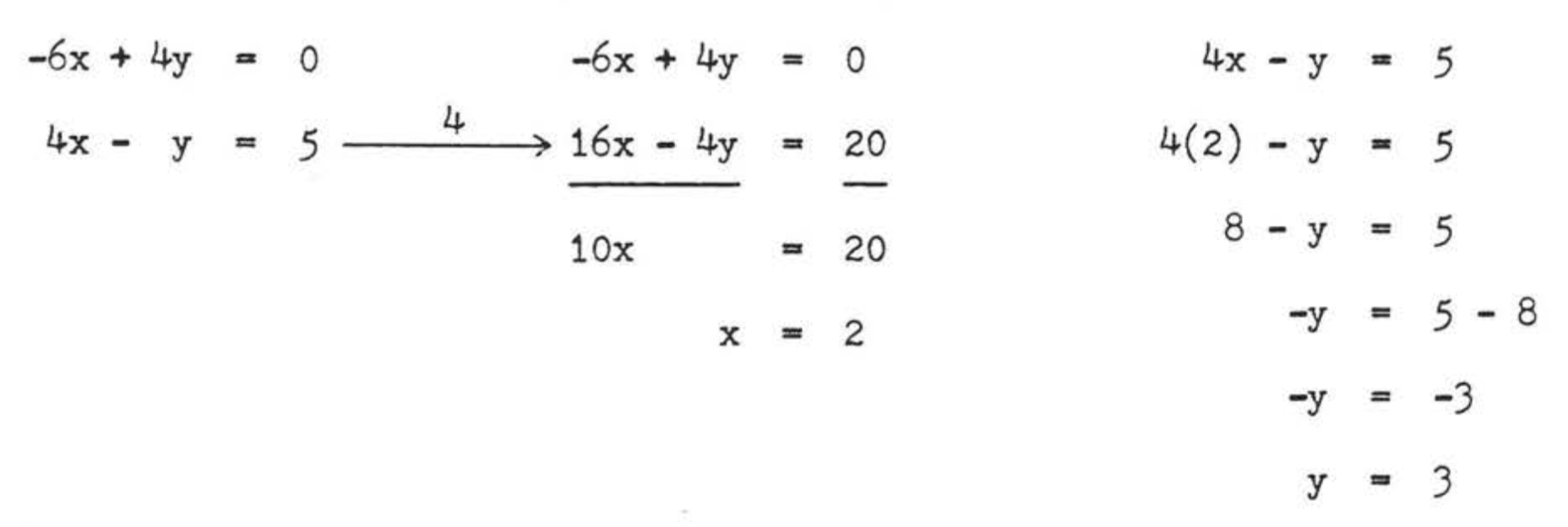
Перевірка:

Відповідь:$x = 2$,$y = 3$,$AC = 11$.

Історична записка

Вважається$\PageIndex{1}$, що теорема про рівнобедрений трикутник вперше була доведена Фалесом (c. 600 B, C,) - це пропозиція 5 в елементах Евкліда. Доказ Евкліда складніше нашого, оскільки він не хотів припускати існування бісектриси кута, доказ Евкліда говорить наступним чином:

Задано$\triangle ABC$ з$AC = BC$ (як на малюнку$\PageIndex{1}$ at the beginning of this section), extend $CA$ to $D$ and $CB$ to $E$ so that $AD = BE$ (Figure $\PageIndex{9}$). Then $\triangle DCB \cong \triangle ECA$ by $SAS = SAS$. The corresponding sides and angles of the congruent triangles are equal, so $DB = EA$, $\angle 3 = \angle 4$ and $\angle 1 + \angle 5 = \angle 2 + \angle 6$. Now $\triangle ADB \cong \triangle BEA$ by $SAS = SAS$. This gives $\angle 5 = \angle 6$ and finally $\angle 1 = \angle 2$.

Малюнок$\PageIndex{9}$: «Міст дурнів».

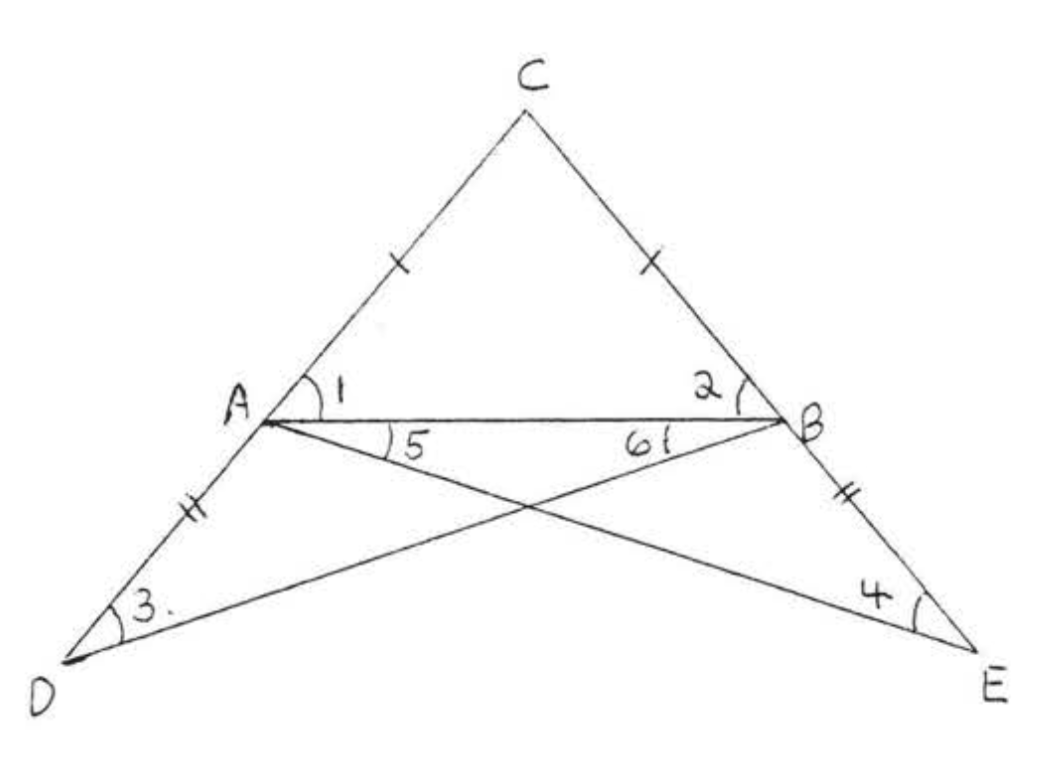
Цей складний доказ відлякував багатьох студентів від подальшого вивчення геометрії протягом тривалого періоду, коли Стихія була стандартним текстом, Малюнок$\PageIndex{9}$ нагадує міст, який в середні століття став відомий як «міст дурнів», Це було нібито тому, що дурня міг не сподіваюся перетнути цей міст і відмовиться від геометрії в цей момент.

Проблеми

Для кожного з наступних станів теорема (и), використана для отримання вашої відповіді.

1. Знайти$x$:

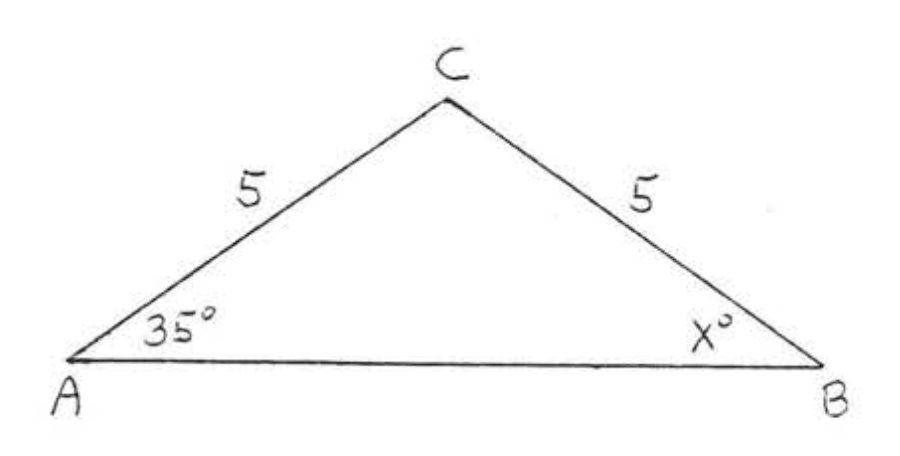
2. Знайти$x$$\angle A$, і$\angle B$:

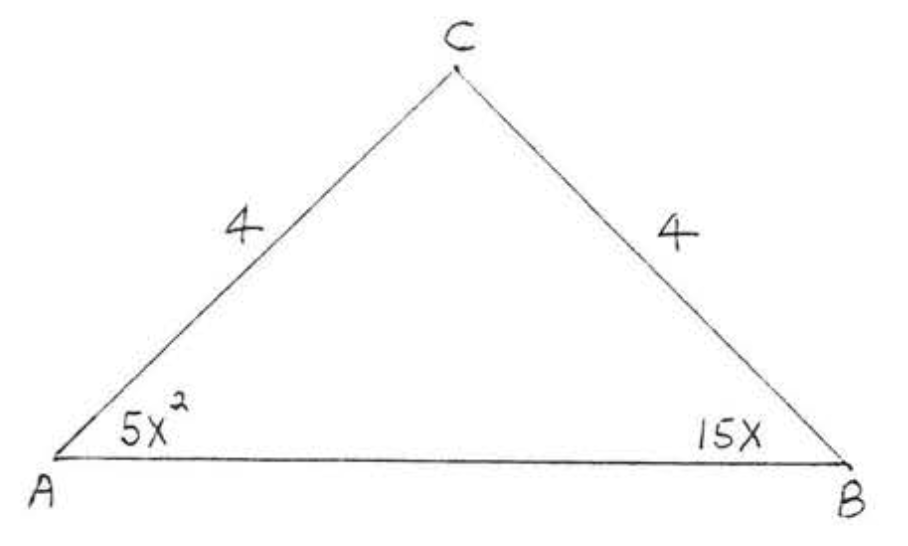
3. Знайти$x$:

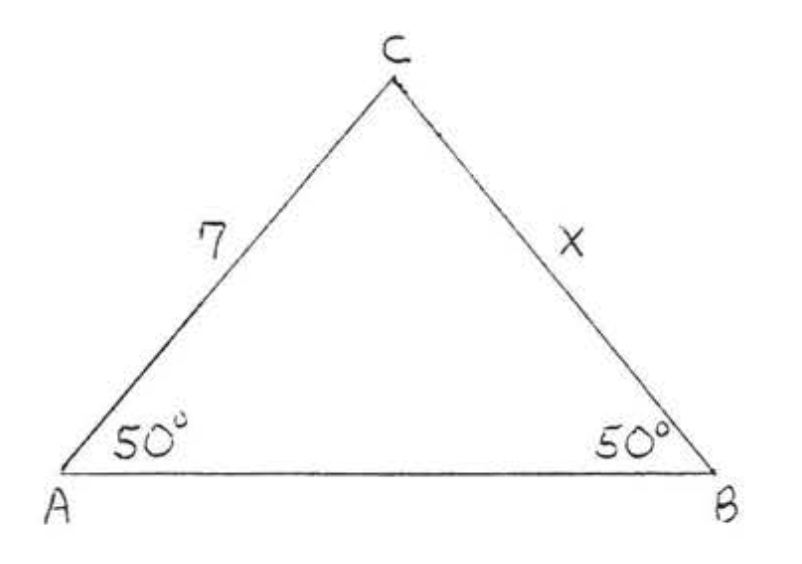
4. Знайти$x$$AC$, і$BC$:

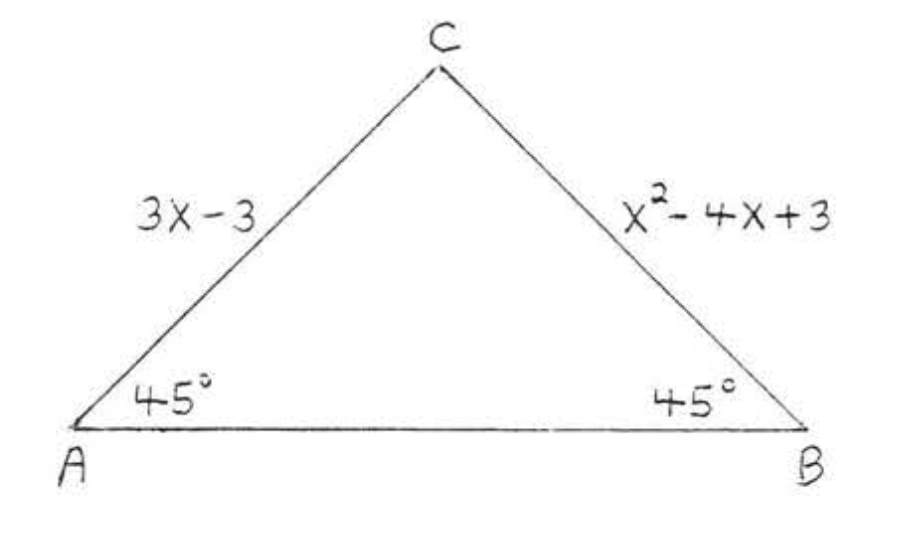
5. Знайти$x$:

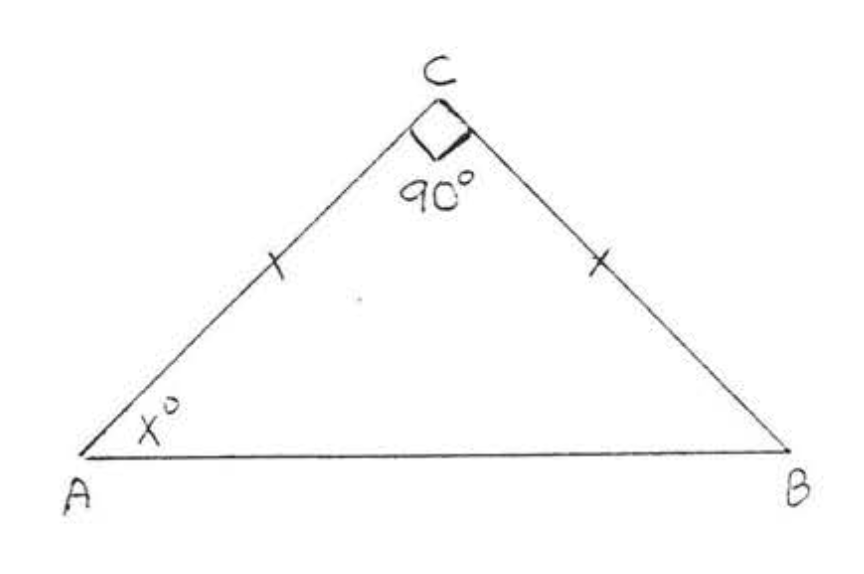
6. Знайти$x$:

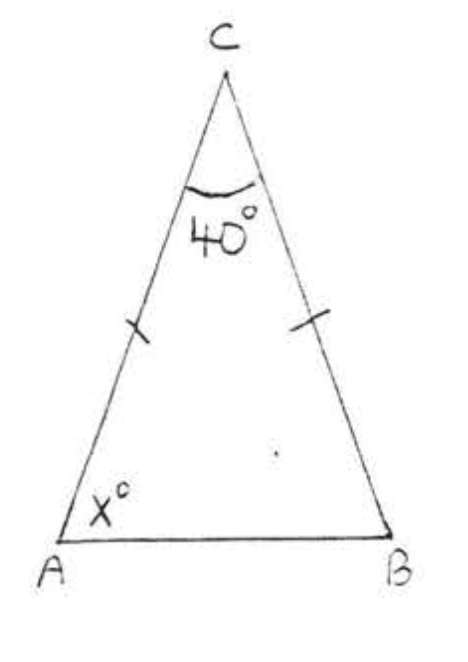
7. Знайти$x, \angle A, \angle B$, і$\angle C$:

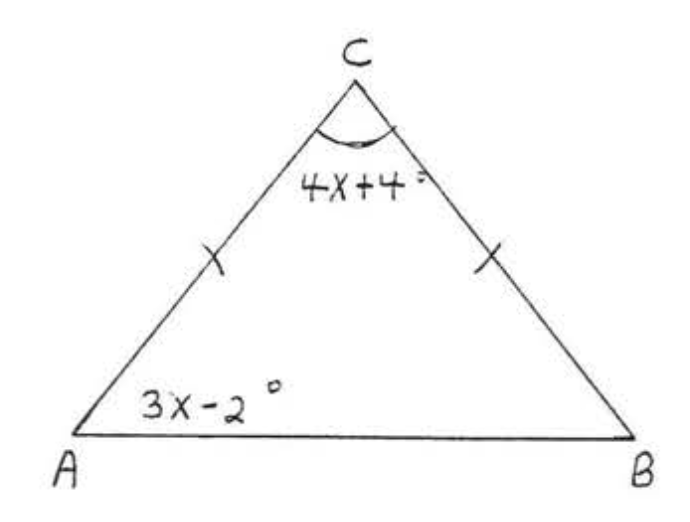
8. Знайти$x, \angle A, \angle B$, і$\angle C$:

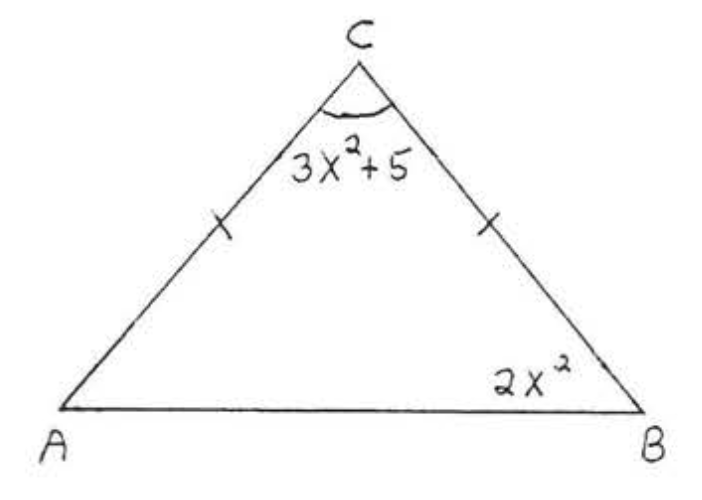
9. Знайти$x, AB, AC$, і$BC$:

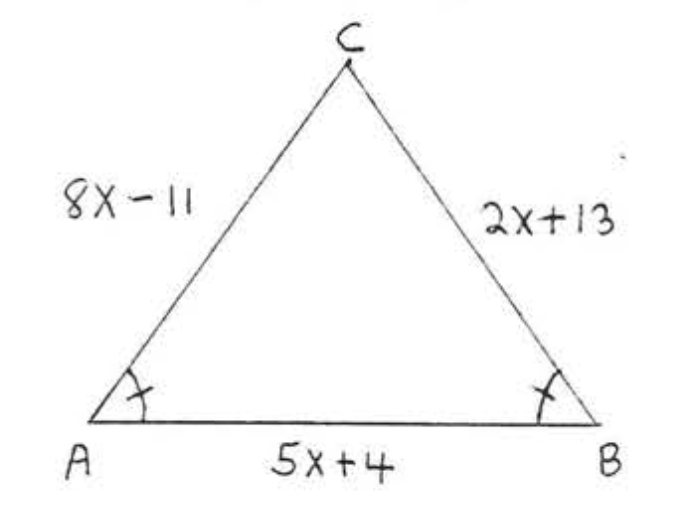
10. Знайти$x, AB, AC$, і$BC$:

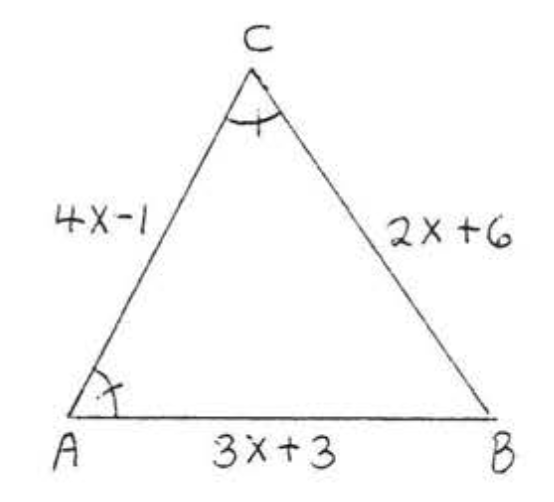
11. Знайти$x, y$, і$AC$:

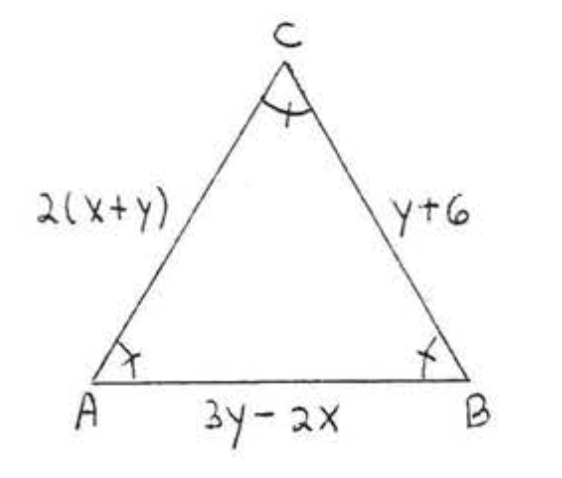
12. Знайти$x, y$, і$AC$:

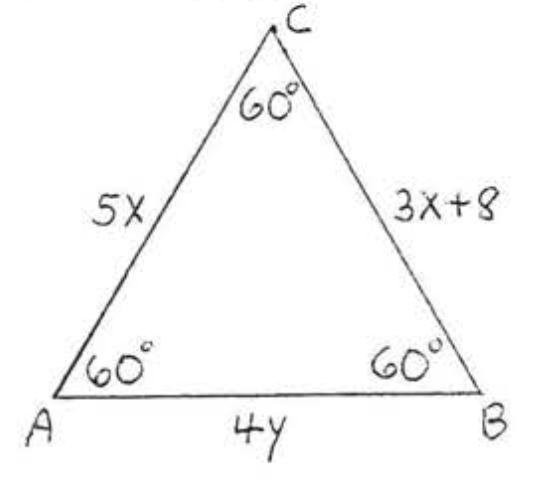
13. Знайти$x$:

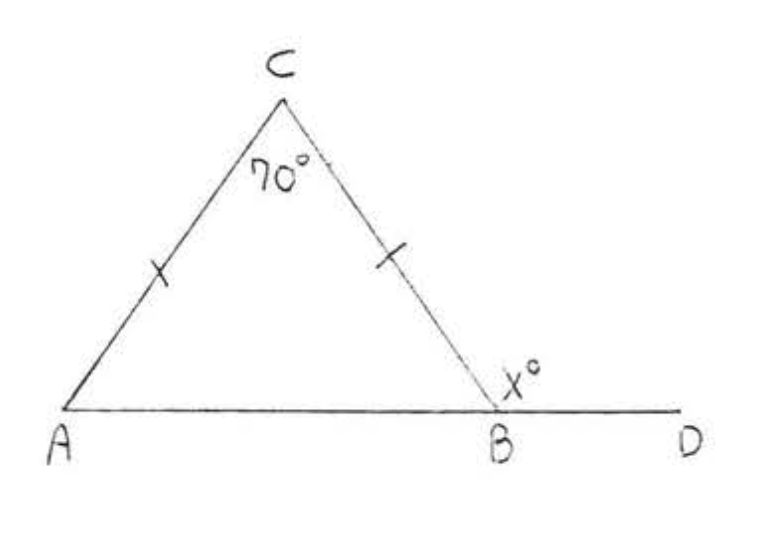
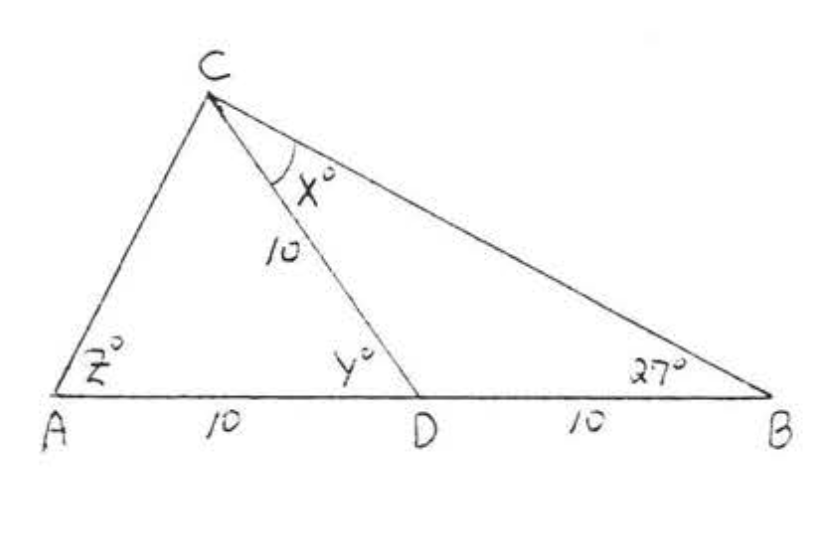
14. Знайти$x, y$, і$z$: