5.9: Теорема Піфагора

Last updated
Save as PDF

Page ID: 57310

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Піфагор був грецьким математиком і філософом, народився на острові Самос (бл. 582 р. До н.е.). Він заснував ряд шкіл, одна, зокрема, в містечку на півдні Італії під назвою Кротоне, члени якого згодом стали називатися піфагорійцями. Близьке коло в школі, Математикоі, жив при школі, позбавляв себе від усіх особистих володінь, були вегетаріанцями, дотримувався суворої обітниці мовчання. Вони вивчали математику, філософію та музику, і вважали, що числа складають справжню природу речей, надаючи числам містичну або навіть духовну якість.

Сьогодні нічого не відомо про працях Піфагора, можливо, через секретність і мовчання піфагорійського суспільства. Однак одна з найвідоміших теорем у всій математиці носить його ім'я, теорема Піфагора.

Перш ніж розкрити зміст теореми Піфагора, зробимо паузу, щоб надати визначення прямокутного трикутника і його складових частин.

Правий трикутник

Трикутник з одним прямим кутом (90 ^◦) називається прямокутним трикутником. На малюнку нижче прямий кут позначений невеликим квадратом.

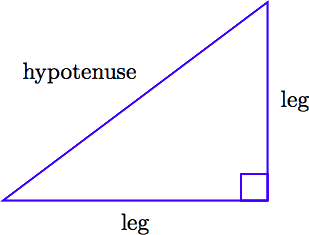
$imageedit_2_4590690964.png$

Сторона трикутника, яка знаходиться прямо навпроти прямого кута, називається гіпотенузою. Сторони трикутника, що включають прямий кут, називаються ніжками прямокутного трикутника.

Тепер ми можемо викласти одну з найдавніших теорем математики, теорему Піфагора.

Теорема Піфагора

$c$Дозволяти представляють довжину гіпотенузи прямокутного трикутника, і нехай a і b представляють довжини його катетів, як показано на зображенні, яке наступне.

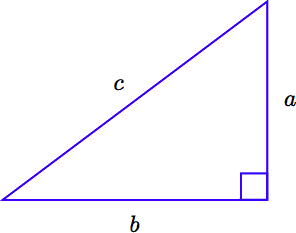
$imageedit_6_3162970942.png$

Співвідношення за участю катетів і гіпотенузи прямокутного трикутника, задане

\[a^2 + b^2 = c^2,\nonumber \]

називається теоремою Піфагора.

Ось два важливих спостереження.

Спостереження щодо гіпотенузи

Двома важливими фактами щодо гіпотенузи прямокутного трикутника є:

Гіпотенуза є найдовшою стороною трикутника і лежить прямо навпроти прямого кута.
У$a^2 + b^2 = c^2$ рівнянні Піфагора гіпотенуза лежить сама по собі на одній стороні рівняння.

Теорема Піфагора може бути застосована тільки до прямих трикутників.

Давайте розглянемо просте застосування теореми Піфагора.

Приклад 1

Ніжки прямокутного трикутника вимірюють 3 і 4 метри відповідно. Знайти довжину гіпотенузи.

Рішення

Давайте дотримуємося вимог до вирішення проблем Word.

1. Налаштуйте словник змінних. Нехай c представляють довжину гіпотенузи, як показано на наступному ескізі.

2. Налаштуйте рівняння. Теорема Піфагора говорить, що

\[a^2 + b^2 = c^2.\nonumber \]

В даному прикладі відомі ноги. Замініть 4 на a і 3 для b (3 для a і 4 для b працює однаково добре) в рівняння Піфагора.

\[4^2 + 3^2 = c^2\nonumber \]

3. Розв'яжіть рівняння.

\[ \begin{aligned} 4^2 + 3^2 = c^2 ~ & \textcolor{red}{ \text{ The Pythagorean equation.}} \\ 16 + 9 = c^2 ~ & \textcolor{red}{ \text{ Exponents first: } 4^2 = 16 \text{ and } 3^2 = 9.} \\ 25 = c^2 ~ & \textcolor{red}{ \text{ Add: } 16+9=25.} \\ 5 = c~ & \textcolor{red}{ \text{ Take the nonnegative square root.}} \end{aligned}\nonumber \]

Технічно є дві відповіді на c ² = 25, тобто c = −5 або c = 5. Однак c являє собою гіпотенузу прямокутного трикутника і повинен бути невід'ємним. Отже, ми повинні вибрати c = 5.

4. Дайте відповідь на питання. Гіпотенуза має довжину 5 метрів.

5. Озирніться назад. Чи задовольняють числа теоремі Піфагора? Сума квадратів катетів повинна дорівнювати квадрату гіпотенузи. Давайте перевіримо.

\[\begin{aligned} 4^2 + 3^2 = 5^2 \\ 16 + 9 = 25 \\ 25 = 25 \end{aligned}\nonumber \]

Все добре!

Вправа

Ноги прямокутного трикутника вимірюють 5 і 12 футів відповідно. Знайти довжину гіпотенузи.

Відповідь: 13 футів

Приклад 2

З огляду на наступний прямокутний трикутник, знайдіть довжину відсутньої сторони.

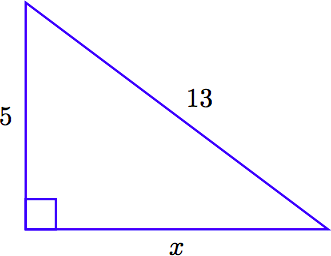
$imageedit_10_6811566794.png$

Рішення

Зверніть увагу, що гіпотенуза (поперек від прямого кута) має довжину 13. Ця величина повинна лежати на одній стороні рівняння Піфагора сама по собі. Сума квадратів ніг йде на іншу сторону. Отже,

\[5^2 + x^2 = 13^2\nonumber \]

Розв'яжіть рівняння для x.

\[ \begin{aligned} 25+x^2 = 169 ~ & \textcolor{red}{ \text{ Exponents first: } 5^2 = 25 \text{ and } 13^2 = 169.} \\ 25 + x^2 -25 = 169 - 25 ~ & \textcolor{red}{ \text{ Subtract 25 from both sides.}} \\ x^2 = 144 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ x= 12 ~ & \textcolor{red}{ \text{ Take the nonnegative square root of 144.}} \end{aligned}\nonumber \]

Вправа

Гіпотенуза прямокутного трикутника має розміри 25 сантиметрів. Одна ніжка прямокутного трикутника має розміри 24 сантиметри. Знайдіть довжину залишилася ноги.

Відповідь: 7 сантиметрів

Ідеальні квадрати - це красиво, але не обов'язково.

Приклад 3

З огляду на наступний прямокутний трикутник, знайдіть точну довжину відсутньої сторони.

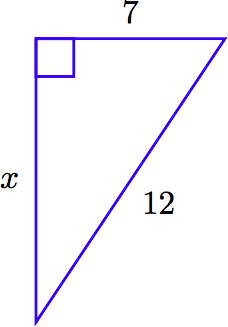
$imageedit_14_5088392393.png$

Рішення

Зверніть увагу, що гіпотенуза (поперек від прямого кута) має довжину 12. Ця величина повинна лежати на одній стороні рівняння Піфагора сама по собі. Сума квадратів ніг йде на іншу сторону. Отже,

\[x^2 + 7^2 = 12^2\nonumber \]

Розв'яжіть рівняння для x.

\[ \begin{aligned} x^2 + 49 = 144 ~ & \textcolor{red}{ \text{ Exponents first: } 7^2 = 49 \text{ and } 12^2 = 144.} \\ x^2 + 49-49 = 144 - 49 ~ & \textcolor{red}{ \text{ Subtract 49 from both sides.}} \\ x^2 = 95 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ x = \sqrt{95} ~ & \textcolor{red}{ \text{ Take the nonnegative square root of 95.}} \end{aligned}\nonumber \]

Значить, точна довжина відсутньої сторони є$\sqrt{95}$.

Вправа

Гіпотенуза і один катет прямокутного трикутника вимірюють 9 і 7 дюймів відповідно. Знайдіть довжину залишилася ноги.

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Важливе спостереження

Будь-яка спроба використовувати ваш калькулятор для наближення 95 у прикладі 3 буде помилкою, оскільки інструкції просили надати точну відповідь.

Іноді бажаний приблизний відповідь, особливо в додатках.

Приклад 4

Джіні хочуть створити город в кутку свого двору у формі прямокутного трикутника. Вона вирізає дві дошки довжиною 8 футів, які формуватимуть ноги її саду. Знайдіть довжину дошки, яку вона повинна відрізати, щоб сформувати гіпотенузу свого саду, поправте до найближчої десятої частини фута.

Рішення

Ми дотримуємося вимог до вирішення проблем Word.

1. Налаштуйте словник змінних. Починаємо з позначеного ескізу. Нехай x представляють довжину невідомої гіпотенузи.

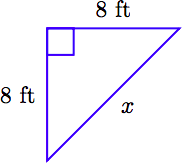
$imageedit_18_8045316766.png$

2. Налаштуйте рівняння. Гіпотенуза виділяється з одного боку рівняння Піфагора.

\[x^2 = 8^2 + 8^2\nonumber \]

3. Розв'яжіть рівняння.

\[ \begin{aligned} x^2 = 8^2 + 8^2 ~ & \textcolor{red}{ \text{ The Pythagorean equation.}} \\ x^2 = 64 + 64 ~ & \textcolor{red}{ \text{ Exponents first: } 8^2 = 64 \text{ and } 8^2 = 64.} \\ x^2 = 128 ~ & \textcolor{red}{ \text{ Add: } 64 + 64 = 128.} \\ x = \sqrt{128} ~ & \textcolor{red}{ \text{ Take the nonnegative square root.}} \end{aligned}\nonumber \]

4. Дайте відповідь на питання. Точна довжина гіпотенузи -$\sqrt{128}$ фути, але нас просять знайти гіпотенузу до найближчої десятої частини фута. За допомогою калькулятора знаходимо наближення для$\sqrt{128}$.

\[\sqrt{128} \approx 11.313708499\nonumber \]

Щоб округлити до найближчої десятої, спочатку визначте округлення і контрольні цифри.

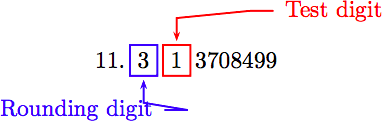
$imageedit_22_8154063398.png$

Тестова цифра менше п'яти. Таким чином, ми залишаємо округлення цифру в спокої і обрізаємо. Тому, поправте до найближчої десятої частини фута, довжина гіпотенузи становить приблизно 11,3 фута.

5. Озирніться назад. Сума квадратів ніжок дорівнює

\[ \begin{aligned} 8^2 + 8^2 = 64 + 64 \\ = 128. \end{aligned}\nonumber \]

Квадрат гіпотенузи дорівнює

\[(11.3)^2 = 127.69\nonumber \]

Вони майже однакові, невідповідність через те, що ми округлили, щоб знайти наближення для гіпотенузи.

Вправа

Сходи на 15 футів спирається на стіну будівлі. Підстава сходів лежить в 5 футах від основи стіни. Наскільки високо вгору по стіні досягає верхня частина сходів? Округлите відповідь до найближчої десятої частини фута.

Відповідь: 14,1 футів

вправи

У вправах 1-16 ваші рішення повинні включати добре позначений ескіз.

1. Довжина одного катета прямокутного трикутника становить 15 метрів, а довжина гіпотенузи - 25 метрів. Знайдіть точну довжину іншої ноги.

2. Довжина одного катета прямокутного трикутника становить 7 метрів, а довжина гіпотенузи - 25 метрів. Знайдіть точну довжину іншої ноги.

3. Довжини двох ніжок прямокутного трикутника складають 12 метрів і 16 метрів. Знайти точну довжину гіпотенузи.

4. Довжини двох ніжок прямокутного трикутника складають 9 метрів і 12 метрів. Знайти точну довжину гіпотенузи.

5. Довжина одного катета прямокутного трикутника становить 13 метрів, а довжина гіпотенузи - 22 метри. Знайдіть точну довжину іншої ноги.

6. Довжина одного катета прямокутного трикутника становить 6 метрів, а довжина гіпотенузи - 15 метрів. Знайдіть точну довжину іншої ноги.

7. Довжини двох ніжок прямокутного трикутника - 2 метри і 21 метр. Знайти точну довжину гіпотенузи.

8. Довжини двох ніжок прямокутного трикутника складають 7 метрів і 8 метрів. Знайти точну довжину гіпотенузи.

9. Довжина одного катета прямокутного трикутника становить 12 метрів, а довжина гіпотенузи - 19 метрів. Знайдіть точну довжину іншої ноги.

10. Довжина одного катета прямокутного трикутника становить 5 метрів, а довжина гіпотенузи - 10 метрів. Знайдіть точну довжину іншої ноги.

11. Довжини двох ніжок прямокутного трикутника - 6 метрів і 8 метрів. Знайти точну довжину гіпотенузи.

12. Довжини двох ніжок прямокутного трикутника складають 5 метрів і 12 метрів. Знайти точну довжину гіпотенузи.

13. Довжина одного катета прямокутного трикутника становить 6 метрів, а довжина гіпотенузи - 10 метрів. Знайдіть точну довжину іншої ноги.

14. Довжина одного катета прямокутного трикутника становить 9 метрів, а довжина гіпотенузи - 15 метрів. Знайдіть точну довжину іншої ноги.

15. Довжини двох ніжок прямокутного трикутника - 6 метрів і 22 метри. Знайти точну довжину гіпотенузи.

16. Довжини двох ніжок прямокутного трикутника складають 9 метрів і 19 метрів. Знайти точну довжину гіпотенузи.

У Вправи 17-24 ваші рішення повинні включати добре позначений ескіз.

17. Довжини двох ніжок прямокутного трикутника складають 3 метри і 18 метрів. Знайти довжину гіпотенузи. Округлите свою відповідь до найближчої сотої.

18. Довжини двох ніг прямокутного трикутника - 10 футів і 16 футів. Знайти довжину гіпотенузи. Округлите відповідь до найближчої десятої.

19. Довжина одного катета прямокутного трикутника становить 2 метри, а довжина гіпотенузи - 17 метрів. Знайдіть довжину іншої ноги. Округлите відповідь до найближчої десятої.

20. Довжина одного катета прямокутного трикутника становить 4 метри, а довжина гіпотенузи - 12 метрів. Знайдіть довжину іншої ноги. Округлите свою відповідь до найближчої сотої.

21. Довжини двох ніг прямокутного трикутника - 15 футів і 18 футів. Знайти довжину гіпотенузи. Округлите свою відповідь до найближчої сотої.

22. Довжини двох ніг прямокутного трикутника - 6 футів і 13 футів. Знайти довжину гіпотенузи. Округлите відповідь до найближчої десятої.

23. Довжина одного катета прямокутного трикутника становить 4 метри, а довжина гіпотенузи - 8 метрів. Знайдіть довжину іншої ноги. Округлите свою відповідь до найближчої сотої.

24. Довжина одного катета прямокутного трикутника становить 3 метри, а довжина гіпотенузи - 15 метрів. Знайдіть довжину іншої ноги. Округлите відповідь до найближчої десятої.

25. Грета і Фріц висаджують 13-метровий на 18-метровий прямокутний сад і викладають його за допомогою мотузки. Вони хотіли б знати довжину діагоналі, щоб переконатися, що утворюються прямі кути. Знайти довжину діагоналі. Округлите свою відповідь до найближчої сотої. Ваше рішення повинно включати добре позначений ескіз.

26. Маркос і Ангеліна висаджують 11- метровий на 19-метровий прямокутний сад, і викладають його за допомогою мотузки. Вони хотіли б знати довжину діагоналі, щоб переконатися, що утворюються прямі кути. Знайти довжину діагоналі. Округлите відповідь до найближчої десятої. Ваше рішення повинно включати добре позначений ескіз.

27. Основа 24-метрового дроту віджиму розташована в 10 метрах від основи телефонного стовпа, який він закріплює. Наскільки високо до полюса досягає дроти хлопця? Округлите свою відповідь до найближчої сотої. Ваше рішення повинно включати добре позначений ескіз.

28. Основа 30-футового дроту хлопця розташована на відстані 9 футів від основи телефонного стовпа, який він закріплює. Наскільки високо до полюса досягає дроти хлопця? Округлите свою відповідь до найближчої сотої. Ваше рішення повинно включати добре позначений ескіз.

29. Пішохідна стежка. Пішохідна стежка проходить через південь протягом 8 кілометрів, потім повертає на захід приблизно на 15 кілометрів, а потім прямує на північний схід прямим шляхом до початкової точки. Скільки триває вся стежка?

30. Тварина стежка. Тварина стежка проходить на схід від водопою на 12 кілометрів, потім йде на північ на 5 кілометрів. Потім стежка повертає на південний захід прямим шляхом назад до водопою. Скільки триває вся стежка?

31. Верхнє вікно. 10-футова сходи спирається на стіну будинку. Наскільки близько до стіни повинна бути нижня частина сходів, щоб досягти вікна 8 футів над землею?

32. Наскільки високо? 10-футова сходи спирається на стіну будинку. Наскільки високою буде сходи, якщо нижня частина сходів знаходиться в 4 футах від стіни? Округлите відповідь до найближчої десятої.

Відповіді

1. 20 метрів

3. 20 метрів

5. √315 метрів

7. $\sqrt{445}$метрів

9. $\sqrt{217}$метрів

11. 10 метрів

13. 8 метрів

15. $\sqrt{520}$метрів

17. 18,25 метрів

19. 16,9 метрів

21. 23,43 футів (ів)

23. 6,93 метра

25. 22,20 метрів

27. 21,82 метра

29. 40 кілометрів

31. 6 футів.