1.4: Модель хижака-здобич Лотка-Вольтерра
- Page ID
- 66655
\(1.4\)Модель хижака-здобич Лотка-Вольтерра
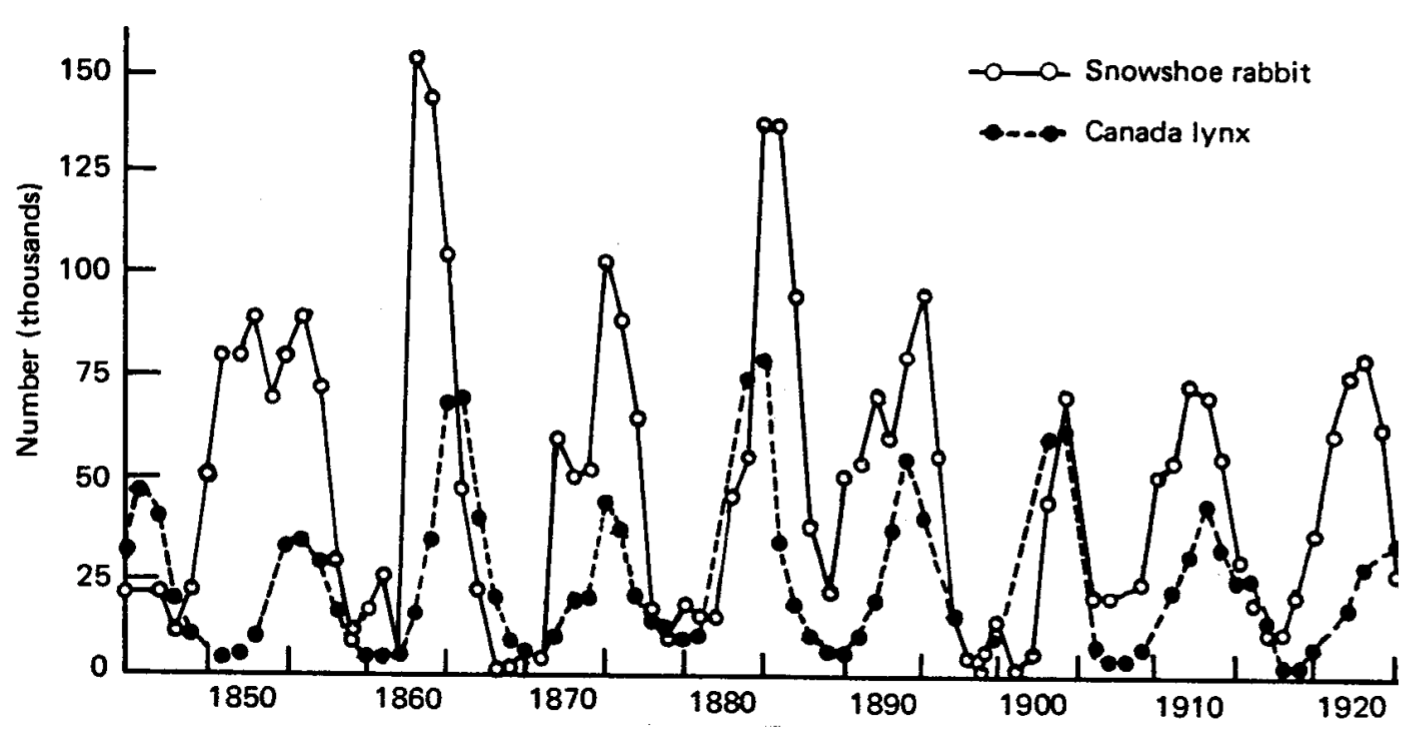
Рекорди торгівлі пелтами (рис. 1.4) компанії Hudson Bay з більш ніж століття демонструють майже періодичні коливання кількості захоплених зайців снігоступів і рисей. З розумним припущенням, що зафіксована кількість тварин, що потрапили в пастку, пропорційна популяції тварин, ці записи свідчать про те, що популяції хижак-здобич, як це характерно для зайця та рисі, можуть коливатися з часом. Лотка і Вольтерра самостійно запропонували в 1920-х роках математичну модель динаміки популяції хижака і здобичі, і ці рівняння Лотки-Вольтерри хижак-здобич з тих пір стали знаковою моделлю математичної біології.
Щоб розробити ці рівняння, припустимо, що популяція хижака харчується популяцією видобутку. Ми припускаємо, що чисельність видобутку зростає в геометричній прогресії за відсутності хижаків (для видобутку є необмежена їжа), і що кількість хижаків за відсутності здобичі розпадається експоненціально (хижаки повинні харчуватися здобиччю або голодувати). Контакт хижаків і видобутку збільшує чисельність хижаків і зменшує кількість здобичі.
Нехай\(U(t)\) і\(V(t)\) буде кількість здобичі і хижаків на час\(t\). Для розробки моделі зв'язаного диференціального рівняння розглянуто розміри популяції в часі\(t+\Delta t\).
Експоненціальний ріст видобутку за відсутності хижаків і експоненціального гниття хижаків за відсутності видобутку можна моделювати звичайними лінійними термінами. Зв'язок між здобиччю і хижаком повинна бути змодельована двома додатковими параметрами. Ми пишемо чисельність населення в той час\(t+\Delta t\) як
\[\begin{aligned} &U(t+\Delta t)=U(t)+\alpha \Delta t U(t)-\gamma \Delta t U(t) V(t) \\[4pt] &V(t+\Delta t)=V(t)+e \gamma \Delta t U(t) V(t)-\beta \Delta t V(t) \end{aligned} \nonumber \]
Параметри\(\alpha\) і\(\beta\) є середньою народжуваністю здобичі на душу населення та смертність хижаків, за відсутності інших видів. Умови зчеплення моделюють контакт між хижаками і здобиччю. Параметр\(\gamma\) - частка здобичі, спійманої на хижака за одиницю часу; загальна кількість здобичі, спійманої хижаками за час,\(\Delta t\) становить\(\gamma \Delta t U V\). Потім з'їдена здобич перетворюється на новонароджених хижаків (розглядають це як перетворення біомаси), з коефіцієнтом перетворення\(e\), так що кількість хижаків протягом часу\(\Delta t\) збільшується на е\ гамма\(\Delta t U V\).
Перетворюючи ці рівняння в диференціальні рівняння шляхом пускання\(\Delta t \rightarrow 0\), отримано відомі рівняння Лотки-Вольтерри хижак-здобич
\[\frac{d U}{d t}=\alpha U-\gamma U V, \quad \frac{d V}{d t}=e \gamma U V-\beta V \nonumber \]
Перш ніж аналізувати рівняння Лотки-Вольтерра, ми спочатку розглянемо аналіз фіксованої точки та лінійної стійкості, застосований до так званої автономної системи диференціальних рівнянь. Для простоти розглянемо систему всього двох диференціальних рівнянь виду
\[\dot{x}=f(x, y), \quad \dot{y}=g(x, y), \nonumber \]
хоча наші результати можна узагальнити до більших систем. Система, надана (1.4.2), вважається автономною, оскільки\(f\) і\(g\) не залежить явно від незалежної змінної\(t\). Фіксовані точки цієї системи визначаються шляхом установки\(\dot{x}=\dot{y}=0\) і рішення для\(x\) і\(y\). Припустимо, що одна фіксована точка є\(\left(x_{*}, y_{*}\right)\). Для визначення його лінійної стійкості розглянуто початкові умови для\((x, y)\) поблизу нерухомої точки з малими незалежними збуреннями в обох напрямках, т. Е\(x(0)=x_{*}+\epsilon(0), y(0)=\)\(y_{*}+\delta(0)\). Якщо початкова збуреність зростає з часом, ми говоримо, що фіксована точка нестабільна; якщо вона розпадається, ми говоримо, що фіксована точка стабільна. Відповідно, ми дозволимо
\[x(t)=x_{*}+\epsilon(t), \quad y(t)=y_{*}+\delta(t), \nonumber \]
і\((1.4.3)\) підставляємо в,\((1.4.2)\) щоб визначити залежність часу\(\epsilon\) і\(\delta .\) Оскільки\(x_{*}\) і\(y_{*}\) є константами, ми маємо
\[\dot{\epsilon}=f\left(x_{*}+\epsilon, y_{*}+\delta\right), \quad \dot{\delta}=g\left(x_{*}+\epsilon, y_{*}+\delta\right) \nonumber \]
Аналіз лінійної стійкості продовжується з припущення, що початкові збурень\(\epsilon(0)\) і\(\delta(0)\) є досить малими, щоб обрізати двовимірне розширення серії Тейлора\(f\) і\(g\) приблизно\(\epsilon=\delta=0\) до першого порядку в \(\epsilon\)і\(\delta\). Зауважимо, що загалом двовимірний ряд Тейлора функції\(F(x, y)\) про походження задається
\[\begin{aligned} F(x, y)=F(0,0)+x F_{x}(0,0) &+y F_{y}(0,0) \\[4pt] &+\frac{1}{2}\left[x^{2} F_{x x}(0,0)+2 x y F_{x y}(0,0)+y^{2} F_{y y}(0,0)\right]+\ldots \end{aligned} \nonumber \]
де терміни розширення можна запам'ятати, вимагаючи, щоб усі часткові похідні ряду погоджувалися з термінами\(F(x, y)\) у походження. Ми зараз Taylor-серії розширюємо\(f\left(x_{*}+\epsilon, y_{*}+\delta\right)\) і\(g\left(x_{*}+\epsilon, y_{*}+\delta\right)\) про\((\epsilon, \delta)=(0,0)\). Постійні терміни зникають, оскільки\(\left(x_{*}, y_{*}\right)\) є фіксованою точкою, і ми нехтуємо всіма термінами з більш високими замовленнями, ніж\(\epsilon\) і\(\delta\). Тому,
\[\dot{\epsilon}=\epsilon f_{x}\left(x_{*}, y_{*}\right)+\delta f_{y}\left(x_{*}, y_{*}\right), \quad \dot{\delta}=\epsilon g_{x}\left(x_{*}, y_{*}\right)+\delta g_{y}\left(x_{*}, y_{*}\right), \nonumber \]
який може бути записаний у вигляді матриці як
\[\frac{d}{d t}\left(\begin{array}{l} \epsilon \\[4pt] \delta \end{array}\right)=\left(\begin{array}{ll} f_{x}^{*} & f_{y}^{*} \\[4pt] g_{x}^{*} & g_{y}^{*} \end{array}\right)\left(\begin{array}{l} \epsilon \\[4pt] \delta \end{array}\right) \nonumber \]
де і\(f_{x}^{*}=f_{x}\left(x_{*}, y_{*}\right)\) т.д. рівняння (1.4.6) являє собою систему лінійних од, і її розв'язання відбувається шляхом прийняття форми
\[\left(\begin{array}{l} \epsilon \\[4pt] \delta \end{array}\right)=e^{\lambda t} \mathbf{v} \nonumber \]
При підстановці\((1.4.7)\) в\((1.4.6)\) та\(e^{\lambda t}\) скасуванні отримано задачу на власні значення лінійної алгебри
\[\mathrm{J}^{*} \mathbf{v}=\lambda \mathbf{v}, \text { with } \mathrm{J}^{*}=\left(\begin{array}{ll} f_{x}^{*} & f_{y}^{*} \\[4pt] g_{x}^{*} & g_{y}^{*} \end{array}\right) \nonumber \]
де\(\lambda\) - власне значення,\(\mathbf{v}\) відповідний власний вектор, і\(\mathrm{J}^{*}\) якобійська матриця, оцінена у фіксованій точці. Власне значення визначається з характеристичного рівняння.
\[\operatorname{det}\left(J^{*}-\lambda I\right)=0 \text {, } \nonumber \]
який для якобійської матриці два на два призводить до квадратного рівняння для\(\lambda\). З форми розв'язку фіксована точка є стабільною\((1.4.7)\), якщо для всіх власних значень\(\lambda\)\(\operatorname{Re}\{\lambda\}<0\), і нестабільною, якщо принаймні для одного\(\lambda, \operatorname{Re}\{\lambda\}>0 .\) Тут\(\operatorname{Re}\{\lambda\}\) мається на увазі дійсну частину (можливо) комплексного власного значення \(\lambda\). Тепер переглянемо рівняння Лотки-Вольтерри. Рішення з фіксованою точкою знаходять шляхом розв'язання\(\dot{U}=\dot{V}=0\), і ми маємо з (1.4.1)
\[U(\alpha-\gamma V)=0, \quad V(e \gamma U-\beta)=0 \nonumber \]
Очевидно, єдиними двома можливими рішеннями є:
\[\left(U_{*}, V_{*}\right)=(0,0) \text { or }\left(\frac{\beta}{e \gamma}, \frac{\alpha}{\gamma}\right) . \nonumber \]
Тривіальна\((0,0)\) фіксована точка нестабільна, оскільки популяція видобутку зростає експоненціально, якщо вона спочатку мала. Для визначення стійкості другої нерухомої точки запишемо рівняння Лотки-Вольтерри у вигляді
\[\frac{d U}{d t}=F(U, V), \quad \frac{d V}{d t}=G(U, V) \nonumber \]
із
\[F(U, V)=\alpha U-\gamma U V, \quad G(U, V)=e \gamma U V-\beta V \nonumber \]
Часткові похідні потім обчислюються як
\[\begin{array}{ll} F_{U}=\alpha-\gamma V, & F_{V}=-\gamma U \\[4pt] G_{U}=e \gamma V, & G_{V}=e \gamma U-\beta . \end{array} \nonumber \]
Якобійський у фіксованій\(\left(U_{*}, V_{*}\right)=(\beta / e \gamma, \alpha / \gamma)\) точці
\[J^{*}=\left(\begin{array}{cc} 0 & -\beta / e \\[4pt] e \alpha & 0 \end{array}\right) \nonumber \]
і
\[\begin{aligned} \operatorname{det}\left(\mathrm{J}^{*}-\lambda \mathrm{I}\right) &=\left|\begin{array}{cc} -\lambda & -\beta / e \\[4pt] e \alpha & -\lambda \end{array}\right| \\[4pt] &=\lambda^{2}+\alpha \beta \\[4pt] &=0 \end{aligned} \nonumber \]
має рішення\(\lambda_{\pm}=\pm i \sqrt{\alpha \beta}\), які є чистими уявними. Коли власні значення якобійців два на два чисті уявні, фіксована точка називається центром і збурень ні зростає, ні розпадається, а коливається. Тут кутова частота коливань дорівнює\(\omega=\sqrt{\alpha \beta}\), а період коливання -\(2 \pi / \omega\).
Ми будуємо\(U\) і\(V\) проти\(t\) (графік часових рядів), і\(V\) проти\(U\) (фазові портрети), щоб побачити, як поводяться рішення. Для нелінійної системи рівнянь типу (1.4.1) потрібно числове рішення.
Рівняння Лотки-Вольтерри має чотири вільних параметра\(\alpha, \beta, \gamma\) і\(e\). Відповідними одиницями тут є час, кількість видобутку, і кількість хижаків. \(\mathrm{Pi}\)Теорема Букінгема передбачає, що нерозмірність рівнянь може зменшити кількість вільних параметрів на три до керованої одновимірної групування параметрів. Ми обираємо невимірність часу, використовуючи кутову частоту коливань та чисельність здобичі та хижаків, використовуючи їх фіксовані точкові значення. За допомогою кареток, що позначають безрозмірні змінні, ми дозволимо
\[\hat{t}=\sqrt{\alpha \beta} t, \quad \hat{U}=U / U_{*}=\frac{e \gamma}{\beta} U, \quad \hat{V}=V / V_{*}=\frac{\gamma}{\alpha} V \nonumber \]
Підстановка (1.4.16) на рівняння Лотки-Вольтерри (1.4.1) призводить до безрозмірних рівнянь
\[\frac{d \hat{U}}{d \hat{t}}=r(\hat{U}-\hat{U} \hat{V}), \quad \frac{d \hat{V}}{d \hat{t}}=\frac{1}{r}(\hat{U} \hat{V}-\hat{V}) \nonumber \]
при одиничному безрозмірному угрупованні\(r=\sqrt{\alpha / \beta} .\) Специфікація\(r\) разом з початковими умовами повністю визначає рішення. Тут слід зазначити, що тривале розв'язання рівнянь Лотки-Вольтерри залежить від початкових умов. Ця асимптотична залежність від початкових умов зазвичай вважається недоліком моделі.
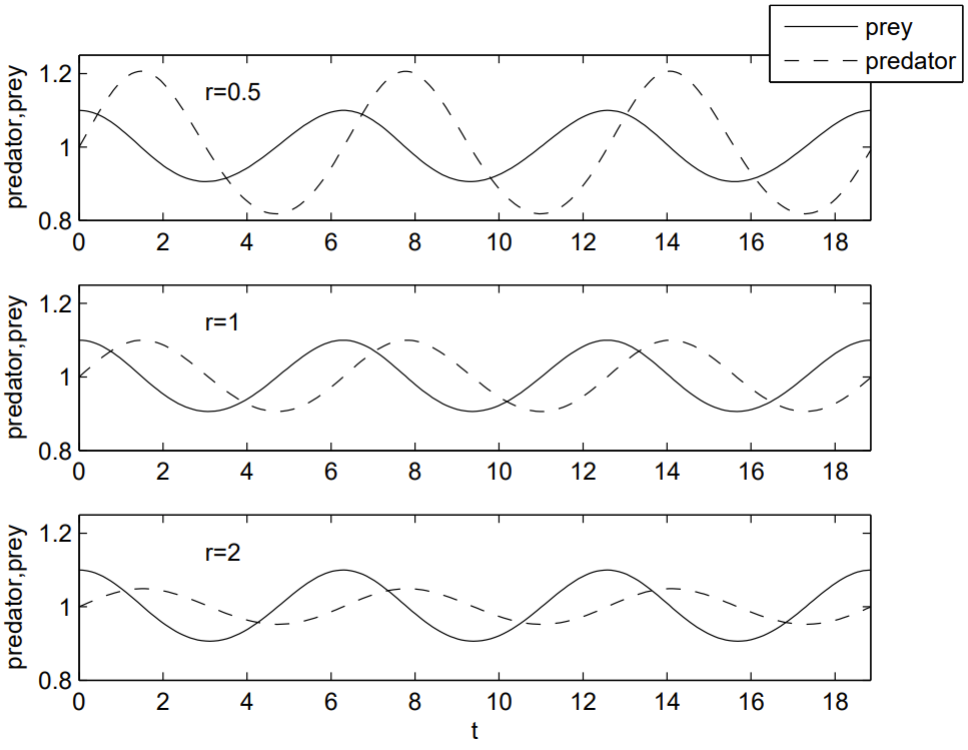
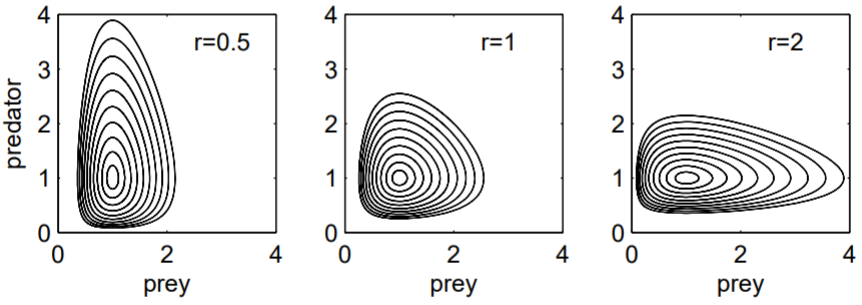
Чисельне рішення використовує вбудовану функцію ODE45.m MATLAB для інтеграції диференціальних рівнянь. Наведений нижче код виробляє рис. 1.5. Зверніть увагу, як популяція хижаків відстає від популяції здобичі: збільшення кількості здобичів призводить до затримки збільшення чисельності хижаків, оскільки хижаки їдять більше здобичі. Фазові портрети чітко показують періодичність коливань. Зверніть увагу, що криві рухаються проти годинникової стрілки: кількість видобутків збільшується, коли кількість хижаків мінімальна, а кількість здобичів зменшується, коли кількість хижаків максимальна.